主蒸汽温度和压力波动对汽轮机转子蠕变疲劳损伤的影响

赵乃龙， 王炜哲， 刘应征

(上海交通大学 动力机械与工程教育部重点实验室； 燃气轮机研究院， 上海 200240)

作为火力发电设备中的重要部件，汽轮机转子的寿命决定了整台机组的寿命[1-4].在电厂实际运行的过程中，不断波动的主蒸汽的温度和压力将致使转子材料产生交变应力和应变，进而影响其高温蠕变疲劳寿命.

图2 主蒸汽的温度和压力以及位置1和位置2的传热系数变化曲线Fig.2 Temperature and pressure curves of the main steam and heat transfer coefficients at Locations 1 and 2

国内外学者针对汽轮机转子的高温蠕变疲劳问题开展了大量研究.荆建平等[5]采用非线性损伤力学模型估算了汽轮机高压转子在实际运行工况下的蠕变疲劳寿命；王坤等[6]对基于有限元模型的大型汽轮机转子寿命评估系统进行了研究；邬文睿[7]根据连续损伤力学理论研究了蠕变疲劳交互作用对汽轮机转子强度的影响；韩炜[8]对某1 000 MW超超临界汽轮机高压转子的低周疲劳寿命损耗和高温蠕变寿命损耗进行了计算与分析，并采用一维有限差分法建立了汽轮机转子应力的在线计算模型.但是，这些研究只考虑了转子在稳态运行过程中的蠕变损伤和启停过程中的低周疲劳损伤，以及两者的相互耦合，没有考虑电厂实际运行过程中主蒸汽温度和压力的波动对转子蠕变疲劳寿命的影响.Kebadze 等[9]采用统计实验的方法研究了某直流蒸汽发电机在运行中的温度波动情况；Samal等[10]建立了一套电厂装置部件损伤的实时评估以及结构的安全评估系统，并考虑了电厂运行过程中蒸汽温度和压力波动所产生的循环应力和应变；Kwon等[11]针对电厂实际运行过程中在蒸汽温度和压力存在波动的情况下某过热箱的寿命进行了研究，结果表明蒸汽温度和压力的波动对过热箱寿命有着至关重要的影响.由此可见，电厂实际运行中蒸汽温度和压力的波动对高温部件的蠕变疲劳强度具有重要影响.

本文以某GW(百万千瓦)级超超临界汽轮机高压转子为研究对象，采用Abaqus有限元软件建立轴对称有限元模型，加载基于电厂实际运行的主蒸汽温度和压力的边界条件，以分析转子在稳态运行过程中的力学行为；采用Lemaitre连续损伤力学模型分析高压转子在实际运行过程中的蠕变疲劳损伤情况，以及主蒸汽温度和压力的波动对转子关键位置热力状态的影响.

1 数学模型

1.1 有限元模型

以图1所示的国产某GW级超超临界汽轮机组高压转子的高温区域为研究对象，采用简化的二维轴对称模型以及二次四边形减缩积分热力耦合单元，并对叶根槽等关键部位的网格进行加密.经过网格收敛性验证，确定计算网格总数为 11 759.

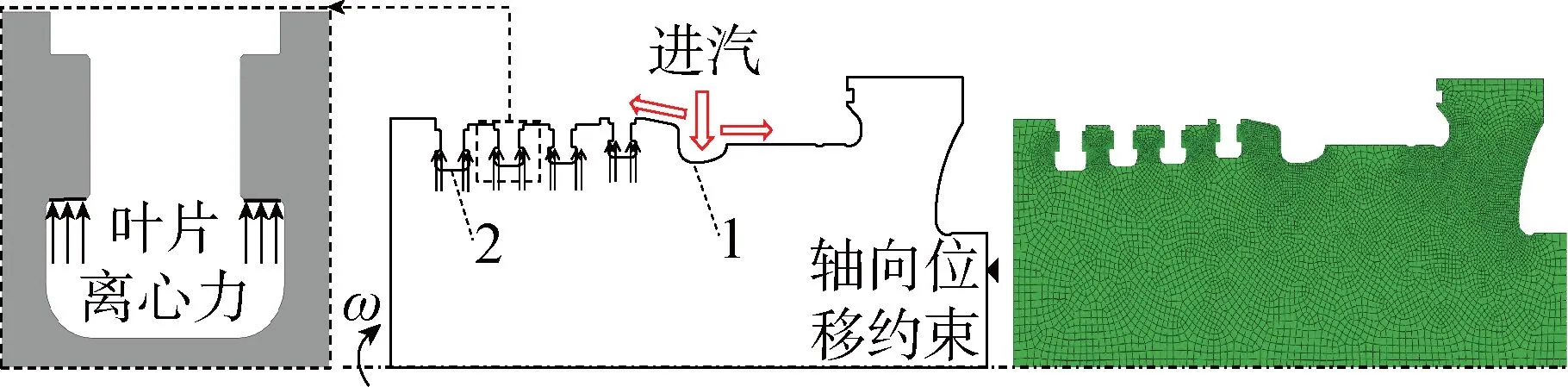
图1 转子几何模型和边界条件及网格划分Fig.1 Geometrical model, boundary condition and meshing of rotor

转子表面与周围蒸汽进行对流换热，采用第3类边界条件进行计算.主蒸汽温度和压力来自于汽轮机厂商提供的现场监测数据(运行时间τ=304 d，即10个月)，由于现场监测数据量庞大，所以本文将数据进行滤波处理，排除不合理的数据，并忽略由传感器误差所致微小波动，在不影响计算准确性的前提下大幅提高了计算效率.转子光轴表面、汽封和叶根槽3个部位的传热系数采用不同公式计算[12-13].在现场运行工况的传热系数计算中，主蒸汽温度和压力随时间的变化而不断波动，导致传热系数不断变化.主蒸汽的温度(t)、压力(p)以及位置1和位置2(见图1)的传热系数(h1，h2)变化曲线见图2.其中，t0和p0分别为主蒸汽的平均温度和平均压力，h01和h02分别为位置1和位置2的平均传热系数.

为对比现场运行工况的影响，本文在主蒸汽的温度和压力保持设计值不变(即理想的设计工况)的条件下对转子进行热力耦合及损伤分析，所用转子的τ为304 d(10个月).转子的额定转速为 3 000 r/min，其自身旋转所产生的离心力以压力形式加载到转子叶根槽承力面，如图1所示.

转子材料选用12%Cr钢，计算中充分考虑了材料力学性能随温度的变化[14].

1.2 本构模型

在有限元模型计算中，采用Ramberg-Osgood模型模拟材料的弹塑性应变-应力关系[15]，即

(1)

式中：ε为总应变；εel为弹性应变；εpl为塑性应变；σ为Von Mises应力；E为弹性模量；K和n′均为与温度相关的材料参数，由汽轮机厂商提供.

针对转子在高温下的蠕变行为，采用时间硬化的Norton-Bailey本构模型[16]进行计算，即

εc=Aσnτm

(2)

式中：εc为蠕变应变；A、n、m均为材料参数，由汽轮机厂商提供.

1.3 连续损伤模型

为了分析转子在高温和高压环境下的蠕变疲劳损伤情况，采用Lemaitre连续损伤力学模型[5,17]计算蠕变疲劳强度，其表达式为[18-19]

dD=dDc+dDf=

(3)

(4)

式中：D为蠕变疲劳的总损伤；N为交变应变次数；Dc为蠕变损伤，dDc为每个时间增量步(dτ)累积的蠕变损伤增量；Df为疲劳损伤，dDf为每次交变应变(dN)累积的疲劳损伤增量；Rv为反映多轴影响的多轴度因子；Δε为总应变；σH为静水压力；ν为泊松比；σeq为等效应力(本文采用Von Mises等效应力)；α1、α2、λ、γ、Ω均为与材料有关的常数.交变应变的提取采用工程上常用的雨流计数法[20].在每步计算中，蠕变疲劳的总损伤值同时影响蠕变损伤增量和疲劳损伤增量，从而体现了蠕变疲劳耦合效应，因此，不能将其简单拆解为蠕变损伤和疲劳损伤之和.

本文采用Python编程语言，基于热力耦合有限元的计算结果，采用有限元后处理的方式进行Lemaitre连续损伤力学模型的模拟.

2 结果与分析

2.1 转子的温度和应力场

图3所示为高压转子在现场工况运行中τ=23，142 d附近蒸汽的温度和压力分布，以及转子的温度和Von Mises应力分布.由图3(c)可见：在τ=23 d附近时，转子的最高温度为 571.8 ℃，温度由进汽口向两端逐渐降低，且呈轴向分布；较大的应力主要分布在转子表面区域，最大应力位于第4级叶根槽圆角部位，为 370.37 MPa.由于叶根槽圆角部位结构复杂、温度梯度较大，所以其承受了较大热应力，而且叶片旋转的离心力直接作用于该部位，从而加剧了应力集中.

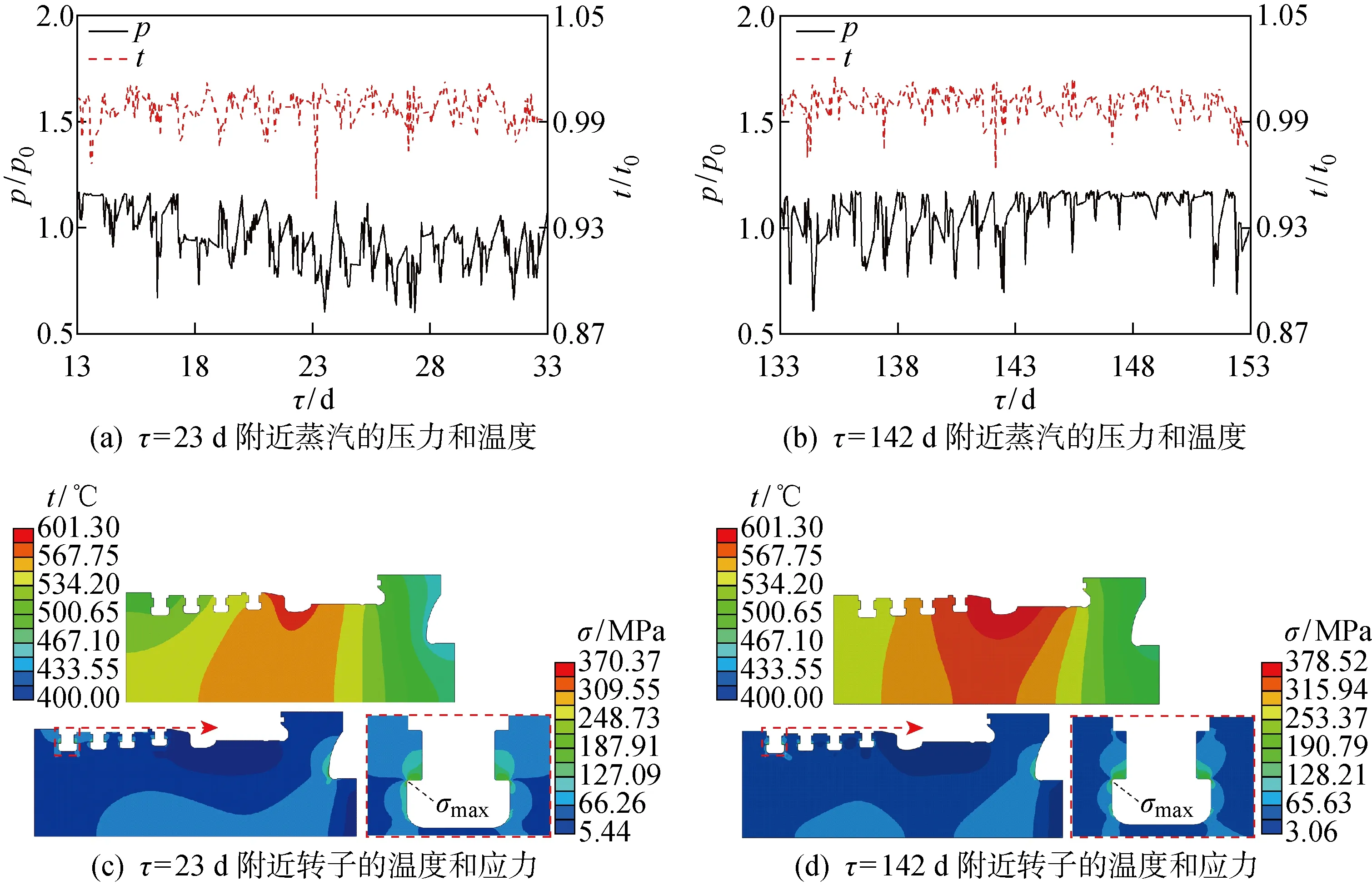
图3 蒸汽的温度和压力及转子的温度和应力分布情况Fig.3 Temperature and stress distributions of the rotor

由图3(d)可见：在τ=142 d附近，转子的最高温度高达 601.3 ℃，温度由进汽口向两端逐渐降低，由于此前主蒸汽的温度快速上升，导致转子表面温度骤升，但转子内部的导热传热较慢，转子中心温度上升缓慢，所以进汽口处的转子表面温度高于中心温度；最大应力仍位于第4级叶根槽圆角部位，为 378.52 MPa，比τ=23 d附近的最大应力增加了 8 MPa.相对于转子应力的绝对值，虽然最大应力的变化不算大，但在转子稳态运行过程中，频繁的主蒸汽温度和压力的变化仍然会对转子的热力状态产生重要影响，将使转子的应力和应变产生变化，从而使得转子的蠕变疲劳损伤不断累积.

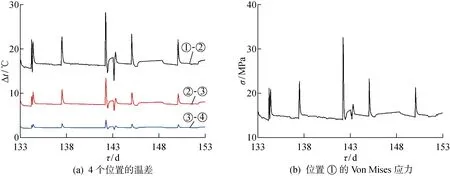
图5 不同特征位置的径向温差和位置①的Von Mises应力变化曲线Fig.5 Temperature differences at different locations and Von Mises stress curve at Location ①

2.2 径向温度和应力

由金属材料的导热原理可知，转子的热应力与局部温度梯度呈正相关关系，因此，合理地控制温度梯度可以有效地降低热应力，从而降低转子的总体应力水平.本文在高压转子温度最高的进汽口部位，从转子表面到中心沿径向等距离选择了4个特征位置(见图4(a))，以研究转子径向温度梯度的变化情况.图4(b)和(c)示出了4个特征位置在电厂实际运行中τ=23，142 d附近的温度变化情况.可以看出：在相同时刻，位置①的温度波动幅度最大；越靠近转子中心，温度的波动幅度越小.这说明在转子内部的热传递过程中，转子材料在导热的同时还发挥了热阻的作用，热阻会减弱温度的波动，从而导致转子的径向温差随着主蒸汽温度和压力的变化而不断波动.

为研究转子的温差与应力之间的关系，图5示出了在现场运行工况下τ=142 d附近4个特征位置的径向温差(Δt)及Von Mises应力的变化情况.由图5(a)可以看出：在相同的时刻，从位置①到位置④的温差逐渐降低，即Δt①-②>Δt②-③>Δt③-④，说明越靠近转子表面的位置，其温度的波动越明显，局部温度梯度越大，所承受的热应力越大；而越靠近转子中心的位置，其温度的波动越小，局部温度梯度越小.由图5(b)可以看出，温差的波动导致位置①的应力出现了波动，交变的应力会导致转子材料的疲劳损伤，而疲劳损伤将与高温蠕变损伤相耦合，从而影响转子的蠕变疲劳强度.

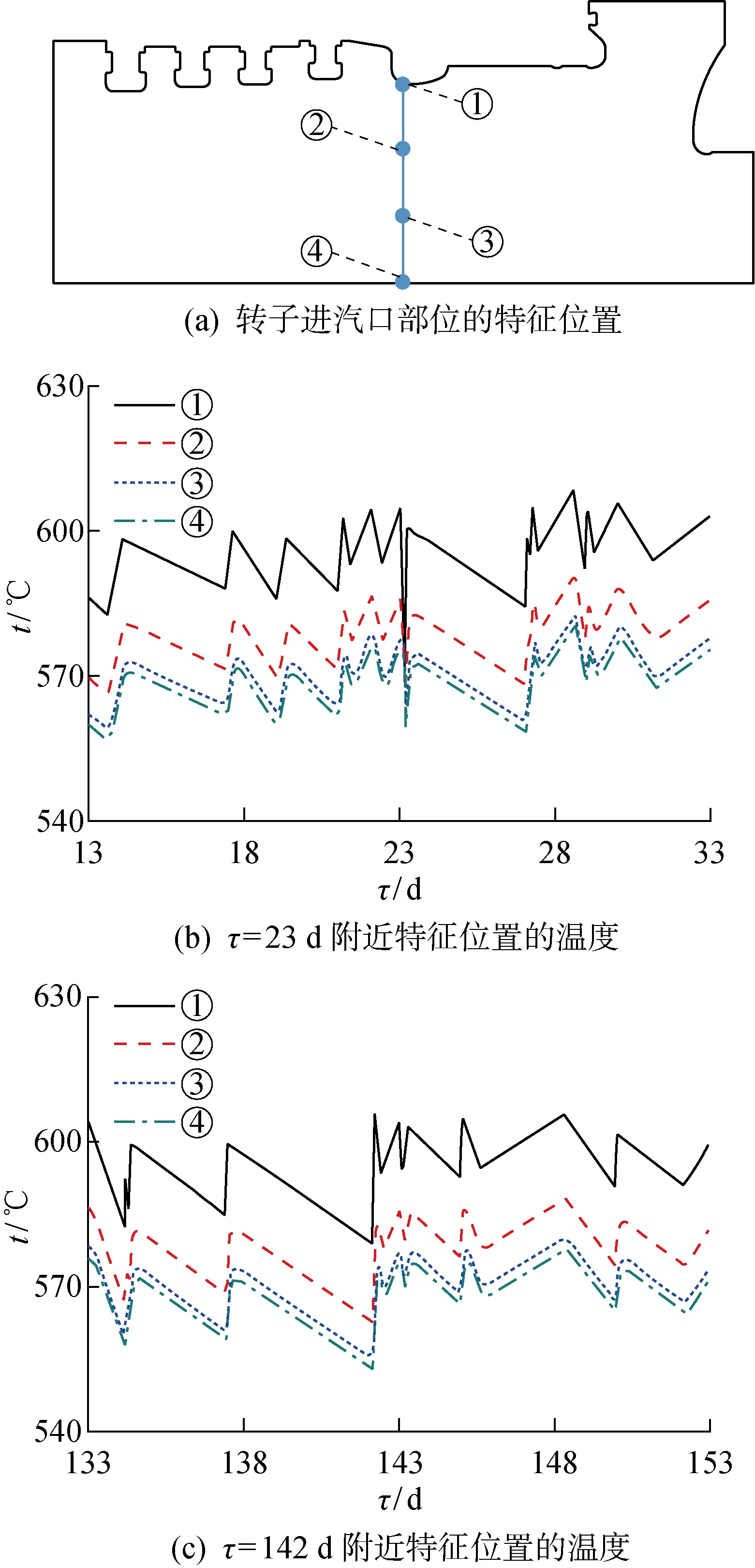
图4 转子进汽口部位的径向温度梯度Fig.4 Radial temperature gradient at the inlet of rotor

2.3 转子的蠕变疲劳损伤

主蒸汽温度和压力的不断波动会通过对流换热来改变转子表面的温度，并通过导热而影响转子内部的温度，但其导热过程相对缓慢，所以转子内部的温差处于不断波动之中，使得转子的热应力产生波动，从而导致转子产生蠕变疲劳损伤.图6所示为利用Lemaitre连续损伤力学模型计算的高压转子在现场工况下运行304 d(10个月)后的蠕变疲劳损伤分布.可以看出，转子大部分区域的损伤趋近于0，损伤较大的部位集中于叶根槽圆角处，与较大Von Mises 应力的分布一致，最大损伤值为 4.53×10-3，出现在第4级叶根槽圆角部位(图6中点C).为进一步说明转子在运行过程中温度和应力的变化及累积损伤情况，本文选取图6中损伤值较大的点B和点C，以及温度最高且不受叶片离心力作用的点A(进汽口位置)作为特征点进行分析.

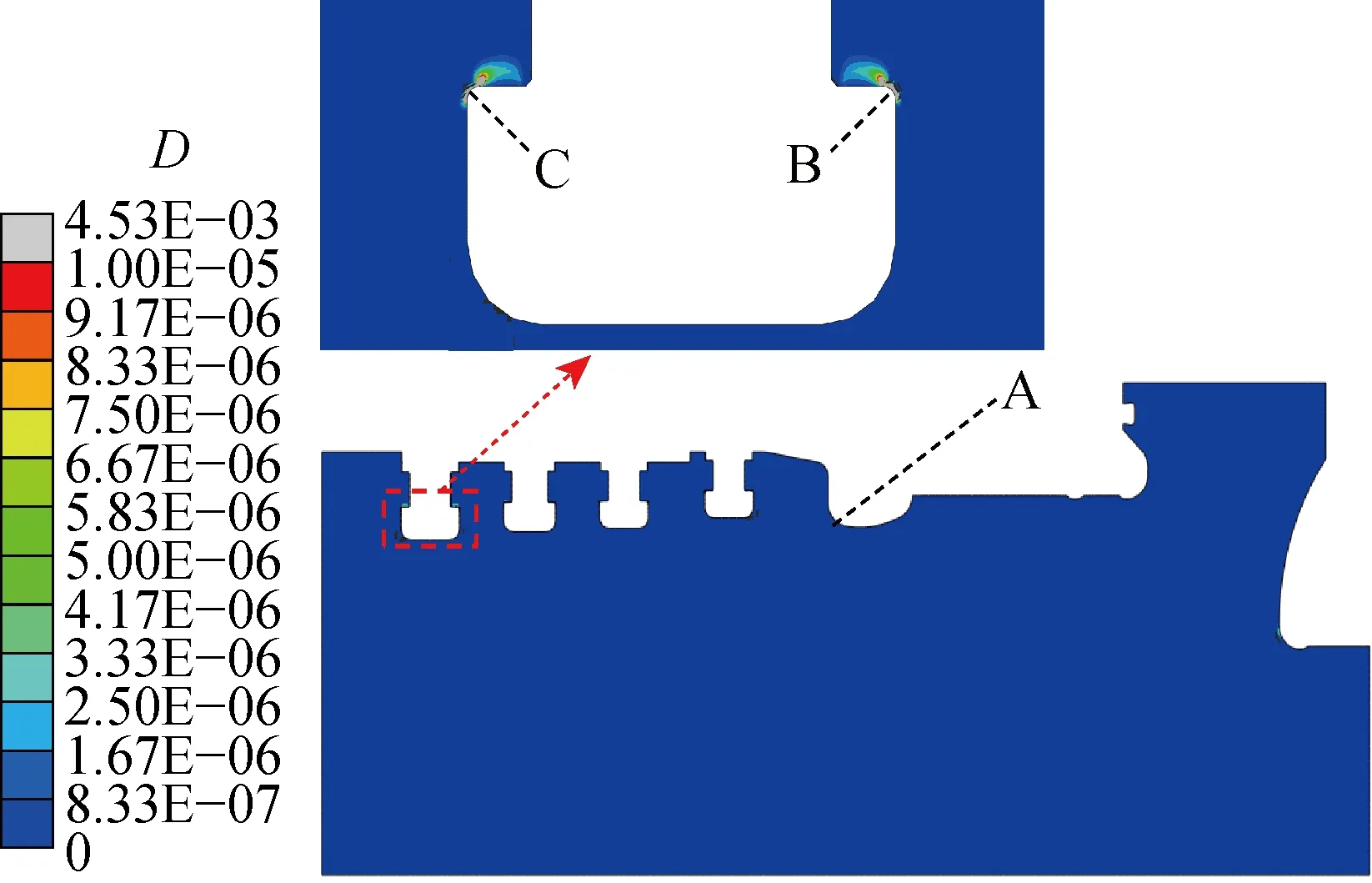
图6 转子的蠕变疲劳损伤分布Fig.6 Creep-fatigue damage distribution of the rotor

图7 3个特征点的温度和Von Mises应力变化曲线Fig.7 Temperature and Von Mises stress curves at three key points

2.4 特征点的温度和应力及损伤

图7所示为在现场运行工况下特征点A，B，C的温度(t1)和Von Mises应力(σ1)随时间变化的情况.为了对比主蒸汽的温度和压力波动所产生的影响，图7中还示出了在参数保持恒定条件下主蒸汽温度(t2)和Von Mises应力(σ2)的变化情况.可见，在现场运行工况下，t1和σ1均随着主蒸汽的温度和压力波动而变化.点A的平均温度和温度波动幅值大于点B和点C，相应地，点A的交变应力幅值也大于点B和点C，从而引起更大的蠕变疲劳损伤；但是，点B和点C受叶片旋转离心力的作用，其平均应力明显高于点A，因此，转子运行时在点B和点C产生了更大的蠕变疲劳损伤.当主蒸汽参数保持恒定时，3个特征点的温度保持稳定，经过304 d(10个月)的运行，点A，B，C的σ2值分别下降了 0.02，4.15，6.23 MPa，这是由于转子产生高温蠕变的缘故.

图8所示为在主蒸汽的温度和压力出现波动(现场运行工况)以及温度和压力保持恒定的条件下3个特征点的蠕变疲劳损伤的变化情况.表1所示为经过304 d(10个月)运行后3个特征点的最终蠕变疲劳损伤值.其中：D1为主蒸汽的温度和压力出现波动时的损伤值；D2为主蒸汽的温度和压力保持恒定时的损伤值.由图8(a)可见，点A的D1值及其增长率明显大于D2值，最终的D1值(9.58×10-8)超过D2值(4.68×10-8)的2倍，这是由于现场运行工况下主蒸汽的温度和压力波动将导致转子材料产生热交变应力和疲劳损伤，进而大幅降低其蠕变疲劳寿命的缘故.在τ=142 d附近，A点的D1值急速上升，说明此时的疲劳损伤和热交变应力很大，这与转子温度最高的时刻相对应(见图3).由图8(b)和(c)可见，点B和点C的D1和D2值非常接近，这是由于点B和点C受到较大的叶片离心力的作用，使得蠕变损伤占据了主要地位，相比之下交变热应力对其蠕变疲劳寿命的影响小得多，因此，主蒸汽的温度和压力波动对疲劳损伤的影响并不显著.

值得注意的是，点B和点C最终的D1值略小于D2值.这是由于在现场运行工况下，为保证安全运行，主蒸汽的温度和压力会尽量保持在低于设计值的状态，很少出现高于其设计值的情况，所以主蒸汽温度和压力的平均值略低于设计值，转子在主蒸汽温度和压力出现波动时的蠕变损伤较小.由于点B和点C的蠕变疲劳损伤占据了主要地位，交变热应力产生的疲劳损伤较小，所以主蒸汽温度和压力出现波动时的总疲劳损伤更小.另外，从损伤力学的角度来看，转子材料的蠕变疲劳损伤取决于材料的有效承载面积，拉伸应力会导致材料中微裂纹和空洞的萌生及扩展，从而降低其有效承载面积，加剧材料损伤；相反，压缩应力会促进微裂纹和空洞的闭合，增大材料刚度，从而降低材料损伤.由于点B和点C的结构复杂，温度梯度较大，主蒸汽温度和压力的波动可能使得该位置承受的挤压作用更强，从而促进了微裂纹和空洞的闭合.该设想还有待于进一步研究验证.

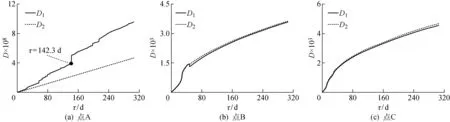
图8 3个特征点的蠕变疲劳损伤变化曲线Fig.8 Damage accumulation curves at points A, B and C

表1 特征点的蠕变疲劳损伤Tab.1 Creep-fatigue damage at the key points

3 结论

(1) 在高压转子现场运行工况下，主蒸汽的温度和压力波动对转子的热力状态产生重要影响.在τ=23 d附近，转子最高温度仅为 571.8 ℃，最大Von Mises应力为 370.37 MPa；在τ=142 d附近，转子最高温度达到 601.3 ℃，最大Von Mises应力达到 378.52 MPa.

(2) 在热传递过程中，越靠近转子表面，其温度的波动越明显，局部温度梯度越大，所承受的热应力越大.

(3) 在高压转子现场运行工况下，转子的温度和应力随着主蒸汽温度和压力的不断波动而变化；点A(进汽口位置)的平均温度和温度波动幅值大于点B和点C(叶根槽圆角处)，但点B和点C受叶片旋转离心力的作用，平均应力明显高于点A.

(4) 对于点A，主蒸汽的温度和压力波动加剧了转子的蠕变疲劳损伤，其疲劳损伤值超过主蒸汽温度和压力保持恒定条件下的2倍；对于点B和点C，主蒸汽的温度和压力波动对蠕变疲劳损伤的影响不显著.