基于最优组合赋权模糊物元模型的节水灌溉项目综合评价

陕振沛，张府柱，张文林，宁宝权

(1.六盘水师范学院 数学与信息工程学院，贵州 六盘水 553004；2.厦门大学信息科学与技术学院，福建 厦门 361005)

节水灌溉项目是一项重要的水利建设工程，对缓解水资源短缺问题，促进农业、林业、畜牧业可持续发展意义重大。影响节水灌溉项目投资决策评价的因素很多，而在这些因素中又有很大部分是不可能完全量化的。因此，如何科学合理地决策，从中选出最优的方案显得至关重要。通过梳理文献资料发现，关于节水灌溉项目评价、优选及投资决策的研究还不少。张文林，张慧愿，陕振沛[1]等提出了决策信息为二参数区间数的节水灌溉项目优选的负理想投影法。王丰凯，吴凤平，于倩雯[2]等提出一种基于格序理论与组合赋权的地区农业节水灌溉项目投资方案优选决策方法。宁宝权，陕振沛[3]建立了改进熵和灰关联分析的模糊物元分析模型将其应用于农业节水灌溉项目优选中。郑和祥，李和平，郭克贞[4]等构建了基于信息熵的模糊物元模型，并对牧区节水灌溉工程后进行评价。陈亮亮，马亮，赵经华[5]采用变异系数法结合TOPSIS模型对某节水灌溉工程建设方案进行优选。通过对这些文献的分析发现：关于节水灌溉项目评价、优选及投资决策的研究以选取模糊物元分析模型作为研究方法的居多，其研究也存在着不足，主要体现在以下几个方面：节水灌溉项目投资决策的评价指标选取的不合理。求取评价指标的权重方法不够科学，要么单一采用主观赋权法或是客观赋权法；即使采用了组合赋权，也是简单粗糙地对主观赋权法和客观赋权法进行组合叠加，求得的组合权重没能更好地反映决策者的主观判断与客观条件约束，没能使组合权重达到最优。评价方法与理论缺乏创新，评价方法单一或是对其进行简单组合。本文在总结现有研究与评价方法的基础上，采用G1法和改进熵权法确定指标的主客观权重，根据最小鉴别信息原理获取最优组合权重。利用物元可拓法和理想解法确定正负理想模糊物元，通过定义待评估节水灌溉项目的相对关联度，构建了基于最优组合赋权模糊物元模型的节水灌溉项目评价模型。并将此模型方法应用在某地区节水灌溉项目投资决策分析中，验证了所提方法的可行性和有效性。

1 最优组合赋权模糊物元模型

1.1 复合模糊物元的构建

物元分析是由我国著名学者蔡文教授于1983年创立的[6]，是研究不相容问题的转化规律与解决方法，其主要思想是将任一事物均用“事物、特征、量值”3个要素来描述，并把这些要素组成的有序三元组的基本元称为物元，适用于多指标评价问题。

给定事物的名称N，它关于C特征的量值为V。如果事物N有n个特征，记为C1,C2,…,Cn，相应的量值记作V1,V2,…,Vn，则物元记为：

(1)

假设有m个节水灌溉项目，每个灌溉项目用n项评价指标及其相应量值来描述，则构成m个节水灌溉项目n维复合模糊物元，记为Rmn，即：

(2)

式中：Mi表示第i个事物(i=1,2,…,m)；Cj表示第j项评价指标(j=1,2,…,n)；xij为第i个节水灌溉项目第j项评价指标对应的模糊量值。

1.2 从优隶属度的确定

一般情况下，评价指标分为正向指标、负向指标两类。正向指标是指数值越大越好的指标，负向指标是指数值越小越好的指标。因此，对评价指标隶属度的计算也分成两类，通过计算指标的隶属度，可以把复合模糊物元矩阵转换为指标的隶属度矩阵。不同的隶属度采取不同的计算公式，而计算隶属度的公式有很多，为了更充分地反映项目评价各指标的相对性，采用如下形式。

对正向指标，其隶属度计算公式为[7]：

(3)

对负向指标，其隶属度计算公式为[7]：

(4)

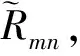
(5)

1.3 理想模糊物元及负理想模糊物元构建

在节水灌溉项目评价从优隶属度模糊物元中，当各属性的指标值都同时达到最优状态时，该模糊物元为理想模糊物元。反之，当各属性的指标值都同时达到最差状态时，该模糊物元为负理想模糊物元。理想模糊物元与负理想模糊物元计算公式如下：

(6)

(7)

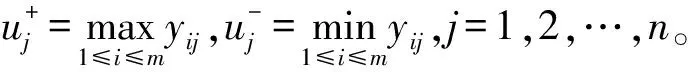
1.4 指标权重确定

(1)改进熵权法确定评价指标的客观权重。熵权法也称熵值法，它是根据指标数据本身来确定指标权重的客观赋权方法。传统的熵权法存在一定的弊端，如：rij=0，rijln (rij)=0， 的特殊约定，同时，当rij=0和rij=1时，rijln (rij)=0，这不管在理论方面还是在现实问题中，这个假设显然是不合理的[8]。为了克服熵权法特殊约定的局限性和弊端，本文对其进行改进，此方法的具体计算步骤如下。

① 计算第j个指标的信息熵[9]。

(8)

(9)

②计算第j个指标的差异系数：

gj=1-ej

(10)

③确定第j个指标的权重：

(11)

(2)G1法确定评价指标的主观权重。

①用G1法确定评价指标的序关系[10]。

②专家给出相邻指标Cj-1与Cj的重要性程度之比rj的理性赋值。

③若专家给出了rj的理性赋值，则第n个评价指标的G1法权重ηn为[10]：

(12)

④由权重ηn可得第n-1,n-2,…,3,2个指标的权重计算公式：

ηj-1=rjηjj=2,3,…,n

(13)

式中：ηj-1为第j-1个评价指标的G1法权重；rj为专家给出的理性赋值；ηj为第j个评价指标的G1法权重。

G1法的赋权特点是通过主观排序反映指标的重要程度, 重要指标赋给较大权重。

(3)组合权重的确定。为了使所求评价指标的权重既能包含决策者的主观判断，又能被客观条件约束，应使所求的组合权重向量W=(w1,w2,…,wn)T与主观权重η=(η1,η2,…,ηn)T、客观权重β=(β1,β2,…,βn)T的距离尽可能地接近。为了实现这一目标，根据最小鉴别信息原理[11]，可建立如下目标函数：

(14)

通过拉格朗日乘子法，求得

(15)

1.5 相对关联度的计算

以M(g+)为模式，根据欧式范数理论，分别计算待评估节水灌溉项目模糊物元与理想模糊物元和负理想模糊物元的关联度，其计算公式如下：

(16)

(17)

式中：wj(j=1,2,…,n)为评价指标的权重。

定义待评估节水灌溉项目的相对关联度，其目的是用来衡量各待评估节水灌溉项目模糊物元与理想模糊物元和负理想模糊物元相距的程度，计算公式为：

(18)

根据待评估节水灌溉项目的相对关联度的大小，对节水灌溉项目进行排序和择优，从式(18)可知， 越小，则其结果越优，最小值者为最优。

2 实例分析

下面以文献[12]中的节水灌溉项目投资决策为例，选取影响节水灌溉项目投资决策的最主要的八大因素：投资X1、投资还本年限X2、自筹投资X3、经济效益X4、节水率X5、内部收益率X6、益本比X7和工程寿命X8为节水灌溉项目投资决策的评价指标，且这8个指标均为正向指标。现根据各项评价指标，对5个节水灌溉项目投资方案进行决策，从中选出最好的方案。原始数据如表1所示。

依据式(2)，则可以建立复合模糊物元Rmn：

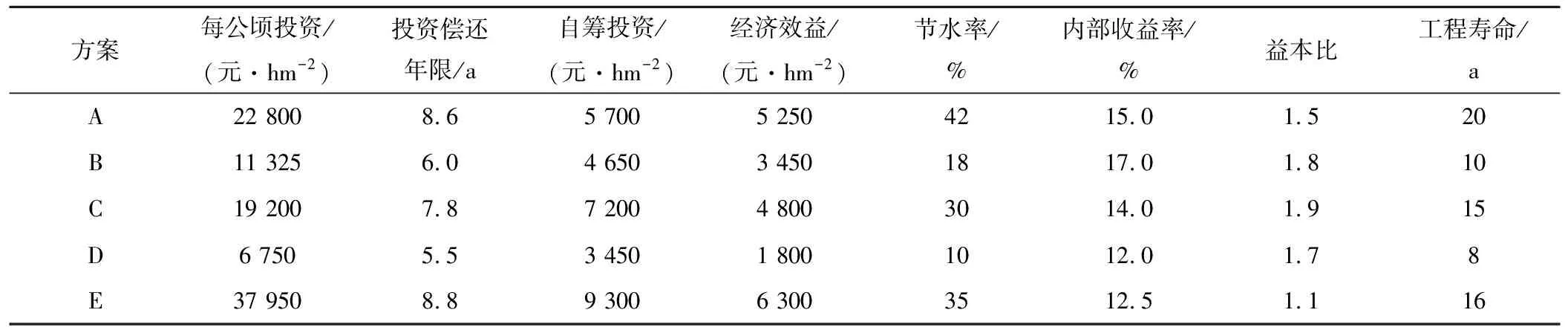
表1 节水灌溉项目经济评价指标

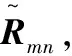
在节水灌溉项目评价从优隶属度模糊物元中，每一个指标(即每一列指标隶属度)的最大值为1、最小值为0，根据公式(6)、(7)构造理想模糊物元与负理想模糊物元，得：

根据改进熵权法公式(8)～(11)求得节水灌溉项目中各评价指标的客观权重，所求结果为：

β=(0.139 3,0.139 0,0.129 3,0.101 8,0.116 4,

0.150 9,0.094 1,0.129 1)T

根据G1法公式(12)、(13)求得节水灌溉项目中各评价指标的主观权重，其结果为：

η=(0.107 0,0.138 1,0.110 0,0.110 9,0.131 3,

0.140 8,0.137 6,0.124 4)T

依据式(15)可求得节水灌溉项目中各评价指标的最优组合权重为：

W=(0.122 6,0.139 1,0.119 7,0.106 7,0.124 1,

0.146 3,0.114 2,0.127 2)T

根据公式(16)、(17)分别计算待评估节水灌溉项目模糊物元与理想模糊物元和负理想模糊物元的关联度，计算结果如下：

将上述求得的待评估节水灌溉项目模糊物元与理想模糊物元和负理想模糊物元的关联度代入式(18)即可求得待评估节水灌溉项目的相对关联度，所得结果为：

E1=0.279 2，E2=0.603 0，E3=0.381 3，

E4=0.931 3，E5=0.298 3

根据待评估节水灌溉项目的相对关联度的大小，对节水灌溉项目进行排序和择优，因为E1E>C>B>D。在这5个方案中，A方案是最好的，其次是方案E。各方案的排序结果与文献[12]中应用模糊综合评判法计算所得排序结果一致，但采用本文方法所得结果相比各方案间差异度更小，更能体现各方案间的差异，说明了所提方法是可行的和有效的。

3 结 语

本文旨在为节水灌溉项目评价、优选及投资决策提出一种新的评价方法，综合本文主要做了以下3个方面的工作：①针对传统熵权法的不足和局限，对熵权法进行改进，使其应用范围更广，更加合理和实用；②根据最小鉴别信息原理获取的组合权重能更好地反映决策者的主观判断与客观条件约束，这样求得的评价指标权重向量更合理；③利用物元可拓法和理想解法确定正负理想模糊物元，根据欧式范数理论，给出了一个新的相对关联度。比单独使用物元可拓法或理想解法更具优越性，实用性和应用性更强。

本文的研究工作丰富了属性的赋权方法，此方法不仅能够应用到节水灌溉项目评价、优选及投资决策中，而且能够应用到其他方面的评价中，所提方法值得借鉴和推广。