超磁致伸缩材料高频磁能损耗特性测试与分析
黄文美 郜春艳 王博文 翁 玲 李亚芳
(1.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室, 天津 300130;2.河北工业大学河北省电磁场与电器可靠性重点实验室, 天津 300130)
0 引言
超磁致伸缩材料Terfenol-D是一种在磁场作用下能发生较大形变的金属功能材料,因其具有磁致伸缩应变大(1.6×10-3)、响应速度快(纳秒级)、能量密度高(2.5×103J/m3)等优点,在大功率水声、超声应用领域优势十分显著[1-2],这些应用都需要Terfenol-D工作于高频驱动磁场条件下。在高频驱动磁化过程中,驱动磁场频率会影响材料有效磁场的大小和滞后性。因此对高频下Terfenol-D磁能损耗进行数值计算及实验分析,是大功率超磁致伸缩换能器结构设计、多场耦合模型研究以及温控系统设计的重要前提和基础[3-5]。
传统意义上磁能损耗被分为磁滞损耗和涡流损耗,其大小是通过标准线圈在不同驱动频率和磁密幅值下的正弦波来进行计算与测量[6],此方法适合于低频且不考虑涡流集肤效应的情况。传统损耗分离法得到的Terfenol-D高频磁能损耗计算值与实测值之间出现较大偏差。当考虑材料内部涡流集肤效应、动态磁滞特性以及磁畴运动等影响因素时,各项损耗系数不再为常数,而是能够反映频率和磁密幅值依赖关系的变量。
文献[7]在考虑驱动频率与磁化方向的基础上,通过改进JA模型来研究损耗动态磁滞特性,其数学表达式参数较多,公式复杂,不适用于实际工程。文献[8]研究了复杂激励条件下磁能损耗计算方法,对环形非晶和纳米晶磁芯进行了磁能损耗测量和实验验证,其适用于中低频激励条件下。文献[9]提出考虑涡流集肤效应的改进铁损计算公式,其计算值与实测值具有较好的一致性,适用于电工钢片损耗计算。
本文沿棒状Terfenol-D轴向和径向分别切片,制成多个方形环状薄片样品,测量在不同驱动磁场频率和磁密幅值下磁能损耗数值,分析磁化方向以及样品尺寸参数对损耗的影响。在损耗分离法的基础上,考虑材料内部涡流集肤效应及动态磁滞特性等影响因素,通过对实测数据进行数值模拟,获得能够反映材料中频率和磁密幅值依赖关系的高频磁能损耗及各项损耗系数变化曲线。通过磁能损耗实测值与计算值对比分析曲线,验证该数值模拟方法对高频下Terfenol-D磁能损耗计算的适用性和正确性。
1 磁能损耗计算方法
现有正弦激励下磁能损耗计算方法主要分为:①以物理现象为依据的磁滞模型。②以实验数据拟合为依据的经验公式法。③以假设损耗可分离为依据的损耗分离法。
1.1 磁滞模型
磁滞模型是以物理现象为基础的损耗模型,主要有Preisach模型和Jiles-Atherton(J-A)模型。Preisach模型是基于磁畴运动在时间与空间上的统计,而J-A模型是基于宏观能量的计算。利用这两种模型来计算磁能损耗具有很高的精度,更适用于静态或准静态条件。由于模型复杂且参数识别过程繁琐,计算量大,使得这两种模型在工程实践尤其是中高频激励下使用较少[10-11]。
1.2 经验公式法
Steinmetz在1892 年提出以实验数据拟合为依托的单位体积内磁能损耗计算方法[12],称之为经验公式法,即
(1)
式中p——磁能损耗f——磁场频率
Bm——磁密幅值
η、α、β——损耗系数
损耗系数与材料磁特性相关。经验公式法涉及的参数少,计算过程简单。此方法忽略了材料各项磁参数及尺寸对磁能损耗的影响,尤其在高频驱动条件下,由此计算的磁能损耗与实测值相差较大,误差不可忽略[13]。
1.3 损耗分离法
损耗分离法是Bertotti根据磁能损耗产生的不同机理提出的计算模型。该模型把损耗分为磁滞损耗、涡流损耗和异常损耗,简化了磁能损耗的分析过程,其计算精度得到了较大的提高[14]。
磁滞损耗ph是铁磁材料在磁化过程中用于克服磁畴旋转摩擦而损失的能量,计算公式为
(2)
式中kh——磁滞损耗系数
损耗系数与材料的本征特性有关[15]。因此当磁密幅值和磁场频率一定时,多个样品之间的损耗差异主要是涡流损耗和异常损耗。
涡流损耗pe与磁密幅值及材料电阻率ρ有关,其计算式为
(3)
式中Ac——材料横截面积
Vc——材料体积
异常损耗pa是铁磁材料中的弛豫现象引发的损耗,与磁场频率、材料磁特性、电阻率等密切相关,其计算表达式为
(4)
式中a、n0——常数
当通入正弦驱动时,单位质量的磁能损耗计算式为
p=ph+pe+pa
(5)
根据式(2)~(5)得出磁能损耗计算式为
(6)
式中ke——涡流损耗系数
ka——异常损耗系数
涡流损耗系数和异常损耗系数变化规律与电阻率、材料尺寸等有关。在高频时,考虑材料内部涡流集肤效应及动态磁滞特性,此时损耗系数不再为常数,而是随频率和磁密幅值变化的变量。
同磁滞模型相比,损耗分离法简化了计算模型,涉及的参数较少;相比于经验公式法,损耗分离法将材料各项磁参数及尺寸对磁能损耗的影响考虑在内,计算精度得以提高,因此逐渐发展用于各类电磁材料及设备的磁能损耗计算[16-18]。
2 实验方法与测试系统
实验中Terfenol-D为薄片环状样品,首先沿着材料径向和轴向分别切片,将其制成外边长10 mm×10 mm,内边长为4 mm×4 mm,厚度为2 mm的方形薄片样品1和样品2。样品1和样品2驱动线圈选用20匝、线径为0.5 mm的漆包线,取样线圈选用10匝、线径为0.15 mm的漆包线。再沿轴向切片,将其制成外边长为20 mm×10 mm,内边长为14 mm×4 mm,厚度为2 mm的长方形薄片样品3,驱动线圈选用66匝、线径为0.5 mm的漆包线,取样线圈选用10匝、线径为0.15 mm的漆包线。如图1所示。

图1 切片样品示意图Fig.1 Schematic of each sample
基于Terfenol-D薄片的动态磁特性测试系统如图2所示。其工作原理:为了给驱动线圈提供所需的正弦交变磁场,首先由信号发生器向功率放大器输入给定频率的正弦交变电流。同时感应电动势从取样线圈的两端产生。环中磁场强度的变化由采样电阻上的电压反映;同时积分放大电路和取样线圈相连,通过放大电路中电容电压来反映材料中磁感应强度的变化。用示波器同时采集通过积分放大电路的感应电动势和通过采样电阻的驱动线圈的信号,将采集到的数据导入计算机中,并绘制出动态磁滞回线。通过计算磁滞回线面积获得磁能损耗[19]。

图2 环状Terfenol-D样品的动态磁特性测试系统Fig.2 Dynamic magnetic measurement system for Terfenol-D1.取样线圈 2.驱动线圈 3.计算机 4.取样线圈接线柱 5.驱动线圈接线柱
3 损耗影响因素
3.1 磁化方向
为了研究磁化方向对Terfenol-D磁能损耗的影响,在驱动磁场频率f=5 kHz时,在不同磁场强度H=3 kA/m和磁密幅值Bm=0.05 T时,分别测试样品1和样品2的动态磁滞回线,从曲线上可以获得振幅磁导率μm及磁能损耗p。
振幅磁导率计算公式为
μm=Bm/(μ0Hm)
(7)
式中μ0——真空磁导率
Hm——磁场强度峰值
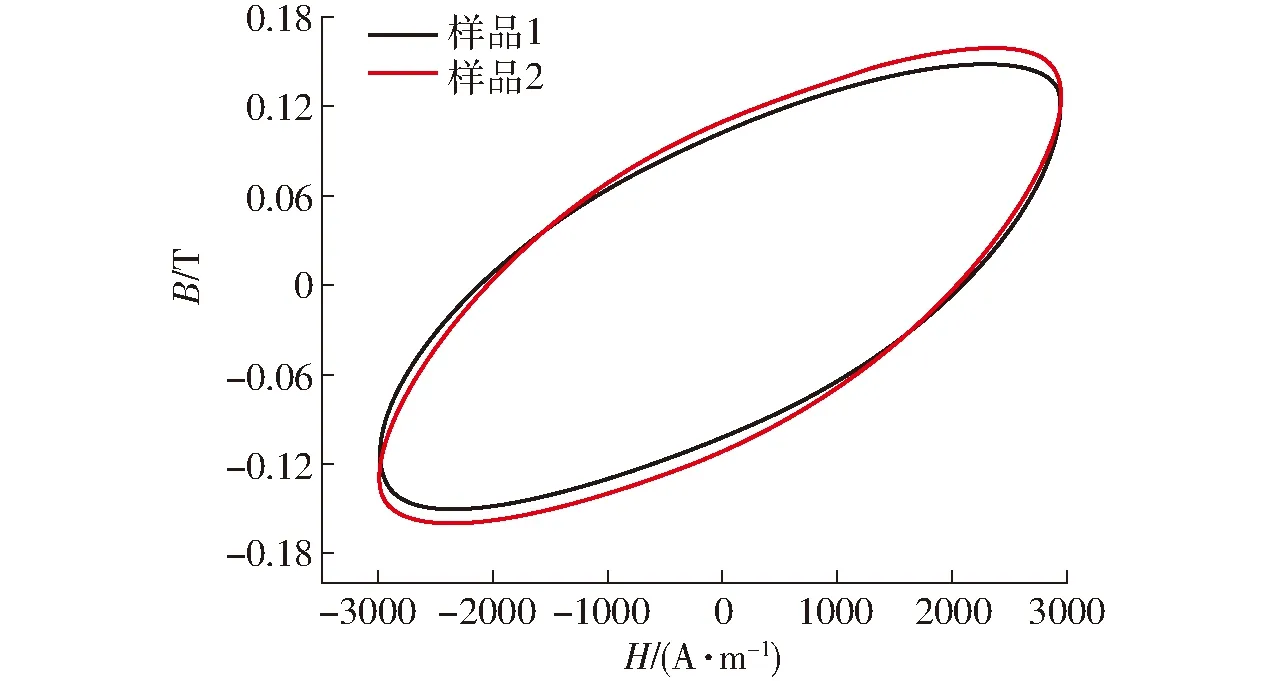
图3 样品1和样品2的动态磁滞回线(H=3 kA/m)Fig.3 Dynamic hysteresis loops of samples 1 and 2 (H=3 kA/m)
图3为Terfenol-D在驱动频率为5 kHz时,H=3 kA/m时各个样品的动态磁滞回线。所测得的各个样品振幅磁导率及磁能损耗如表1所示。其中样品2与样品1相比,曲线上横向变宽、面积增大,其振幅磁导率较高,产生的磁密幅值较大。
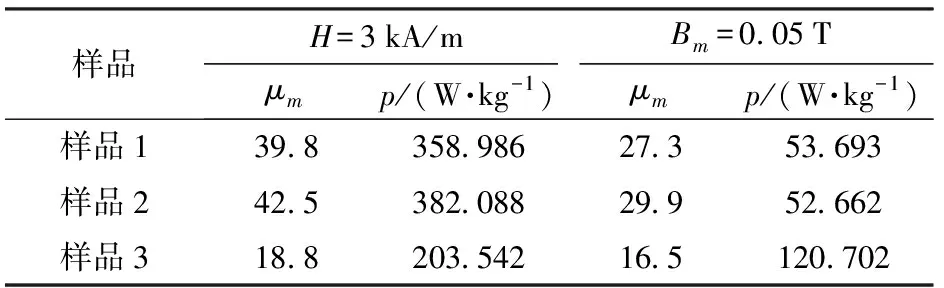
表1 各个样品的数据对比Tab.1 Data comparison of each sample
图4为Terfenol-D在驱动频率为5 kHz时,Bm=0.05 T时各个样品的动态磁滞回线。所获振幅磁导率以及磁能损耗如表1所示。其中样品1与样品2相比,曲线上横向变宽、面积增大。当磁密幅值一定时,样品2所需磁场强度较小,振幅磁导率较高且磁能损耗较低。

图4 样品1和样品2的动态磁滞回线(Bm=0.05 T)Fig.4 Dynamic hysteresis loops of samples 1 and 2 (Bm=0.05 T)
由此可知材料磁化方向对材料本身包括振幅磁导率和磁能损耗等磁特性参数产生影响,在沿着棒状材料的轴心方向(轴向),即Terfenol-D易磁化方向上,材料具有较好的导磁性和低损耗特性[20]。
3.2 尺寸参数
为了探究样品尺寸对Terfenol-D磁能损耗的影响,在驱动磁场频率f=5 kHz时,在不同磁场强度H=3 kA/m和磁密幅值Bm=0.05 T时,分别测试样品2和样品3的动态磁滞回线。
图5为Terfenol-D在驱动频率为5 kHz时,H=3 kA/m时各个样品的动态磁滞回线。所获振幅磁导率以及磁能损耗如表1所示。可以看出,样品2和样品3相比而言,其曲线横向变宽、面积增大,振幅磁导率较高,产生的磁密幅值较大。
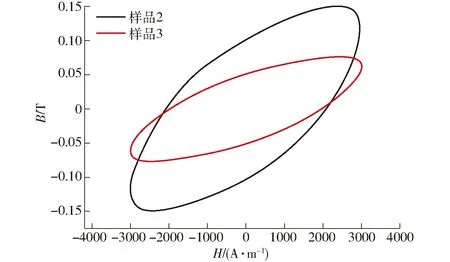
图5 样品2和样品3的动态磁滞回线(H=3 kA/m)Fig.5 Dynamic hysteresis loops of samples 2 and 3 (H=3 kA/m)
图6为Terfenol-D在驱动频率为5 kHz时,Bm=0.05 T时各个样品的动态磁滞回线。所获振幅磁导率以及磁能损耗如表1所示。可知,样品3与样品2相比而言,其曲线上横向变宽、面积增大。当磁密幅值一定时,样品2 所需的磁场强度较低,磁能损耗较低,振幅磁导率较高。由此可知,为保证高导磁特性的同时能够降低材料磁能损耗,在设计以Terfenol-D为核心部件的超磁致伸缩换能器件时,需考虑材料横截面积、叠片厚度以及体积等尺寸参数。
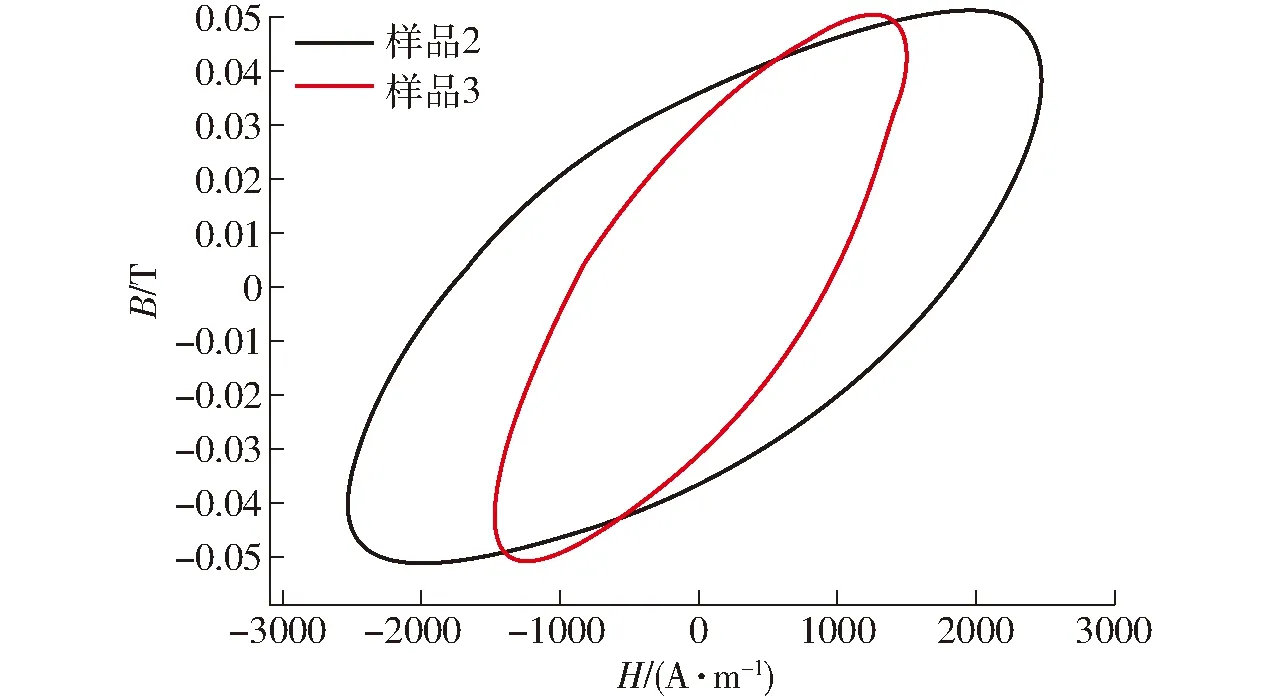
图6 样品2和样品3的动态磁滞回线(Bm=0.05 T)Fig.6 Dynamic hysteresis loops of samples 2 and 3 (Bm=0.05 T)
4 磁能损耗实测值与计算值对比
4.1 损耗系数
以样品1的实测数据为例,据1~20 kHz的实测损耗数据进行数值模拟获得各项损耗系数kh、α、ke、ka,分析其变化趋势。图7~9为各项损耗系数随着磁密幅值变化曲线。由图可知,当考虑材料内部涡流集肤效应、动态磁滞特性以及磁畴运动等影响因素时,各项损耗系数不再为常数,而是能够反映频率和磁密幅值依赖关系的变量。
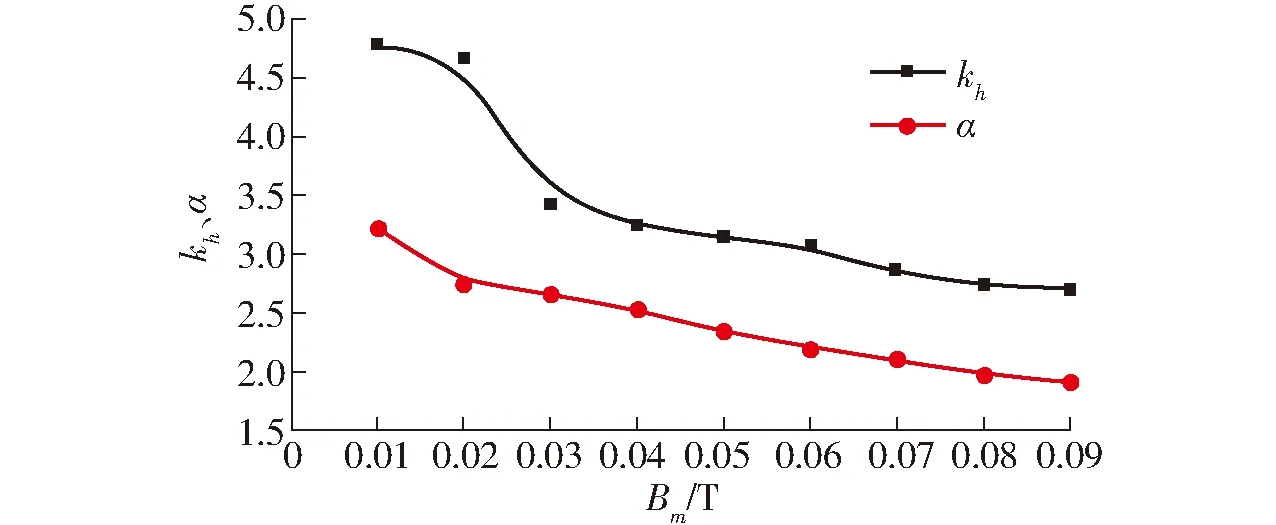
图7 磁滞损耗系数kh和α随磁密幅值变化曲线Fig.7 Changing curves of hysteresis losses coefficients with magnetic density

图8 涡流损耗系数ke随磁密幅值变化曲线Fig.8 Changing curves of eddy current losses coefficient with magnetic density
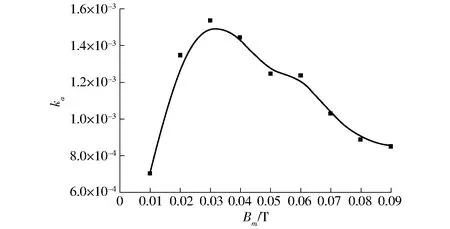
图9 异常损耗系数ka随磁密幅值变化曲线Fig.9 Changing curves of anomalous losses coefficient with magnetic density
磁滞损耗系数、涡流损耗系数及异常损耗系数虽然是通过曲线拟合获得的,但可通过变化关系对各项系数进行物理意义的解释。在考虑高频下涡流集肤效应以及动态磁滞特性的基础之上,磁滞损耗系数kh、α随磁密幅值增大而减小(图7),反映了材料磁滞回线面积变化趋势及内部磁畴壁的运动情况。涡流损耗系数ke受到涡流集肤效应的影响,涡流损耗系数逐渐增大(图8)。当材料在弱磁场驱动下,磁畴壁缓慢运动,强磁场驱动下磁畴快速运动,被磁化到饱和状态时,磁畴壁消失,异常损耗系数逐渐减小,与硅钢片ka规律一致[3,9](图9)。
4.2 磁能损耗实测值与计算值对比与分析
在考虑材料内部涡流集肤效应及动态磁滞特性等影响因素的基础上,对高频磁能损耗实测数据进行数值模拟,得到模拟计算值与实测值对比曲线,如图10、11所示,图中实心点为实测值,空心点为计算值。
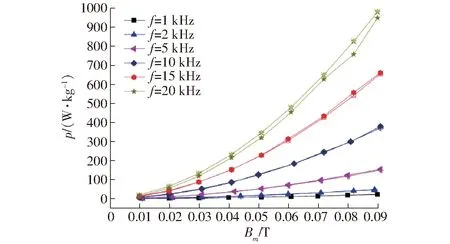
图10 不同频率下损耗模拟值与实测值对比曲线Fig.10 Comparison curves of simulated and measured losses at different frequencies
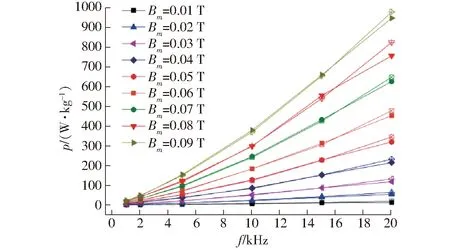
图11 不同磁密幅值下模拟值与实测值对比曲线Fig.11 Comparison curves of simulated and measured losses at different magnetic densities
不同频率下磁能损耗随磁密幅值的变化曲线如图10所示。可以看出,磁能损耗实测值随磁密幅值的变化趋势与数值模拟法所得计算值保持一致,变化趋势为数值增大,增速加快。当频率为5 kHz时,随着磁密幅值从0.01 T到0.09 T时,损耗实测值从2.742 W/kg变化到153.890 W/kg,增加了55.12倍。
不同磁密幅值下损耗数值模拟所得的计算值与实测值随频率变化对比曲线如图11所示,当磁密幅值为0.05 T时,频率从1 kHz到20 kHz,损耗从8.138 W/kg增加到319.428 W/kg,损耗增加了38.25倍。图10和图11表明,当频率低于5 kHz时,磁能损耗增速较缓。当频率大于5 kHz时,损耗增速较快。当峰值通量密度低于0.05 T时,损耗增长缓慢。当峰值通量密度高于0.05 T时,损耗增长较快。
图12为不同频率下损耗数值模拟的计算值与实测值的误差随磁密幅值变化曲线,由图可知,低频低磁密幅值时损耗数值模拟的计算值和实测值之间最大误差为15%,随着频率的升高,误差逐渐变小,5~15 kHz之间平均误差为4%;随着磁密幅值的增大,误差逐渐变小,当磁密幅值高于0.05 T时,计算值和实测值的平均误差为3%,说明考虑涡流集肤效应以及动态磁滞特性的数值模拟方法适用于高频磁能损耗的计算,可用于预测实验范围内其他频率段的Terfenol-D磁能损耗。

图12 不同频率下误差随磁密幅值变化曲线Fig.12 Changing curves of error with magnetic density at different frequencies
5 结论
(1)考虑磁化方向的影响时,当磁场强度为定
值时,沿易磁化方向切片的样品2相比样品1而言磁导率较高,磁密幅值较大。当磁密幅值为定值时,样品2所需的磁场强度较低,磁能损耗较小。考虑尺寸参数的影响时,当磁场强度为定值时,尺寸参数小的样品2相比于样品3而言磁导率较高,磁密幅值较大,当磁密幅值为定值时,样品2磁导率高,所需磁场强度较小。可用于指导高频磁致伸缩换能器件的电磁和机械结构设计。
(2)通过对比磁能损耗数值模拟的计算值与实测值可知,各项损耗系数在高频下不为常数,而是随着频率和磁密幅值变化的变量,所采用的基于损耗分离法和少量实验数据的考虑涡流集肤效应及动态磁滞特性的损耗数值模拟方法适用于高频下磁致伸缩材料的磁能损耗计算,可作为建立磁致伸缩材料和器件在高频激励条件下多场耦合模型的基础。

