天然气水合物输送管道的压力损失规律

徐海良，胡文港，杨放琼



天然气水合物输送管道的压力损失规律

徐海良1, 2，胡文港1，杨放琼1, 2

(1. 中南大学 机电工程学院，湖南 长沙，410083；2. 中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083)

为了研究海底天然气水合物绞吸式开采水力输送系统中管径、流速、体积分数和颗粒粒径对输送系统压力损失的影响规律，确定各参数的合理选择范围；建立输送管道三维流场模型，采用控制变量的方法，运用计算流体力学理论和Fluent仿真软件对输送管道内固液两相流场进行仿真分析。研究结果表明：输送系统压力损失梯度随管径的增大而减小；当管径增大到0.4 m时，继续增大管径对压力损失梯度影响越来越小；压力损失梯度随浆体流速的增大先减小后增大，存在1个最优流速，在2.5~4.0 m/s之间，且颗粒粒径和体积分数越大，对应的最优流速就越大，压力损失梯度随体积分数的增大呈线性增大；压力损失梯度随着颗粒粒径增大而增大，但增大幅度很小。

天然气水合物；水力输送；压力损失；模拟仿真

传统化石燃料的大量开采使人类面临资源枯竭和环境污染两大难题，近年来，人们对新型清洁能源的探索和开发显得尤为迫切。天然气水合物是天然气和水在低温高压条件下形成的结晶体，在地球上储量巨大，能量密度高而且燃烧后不会产生污染物，因此，天然气水合物的开采方案研发成为全世界的焦点[1−3]。地球上已探明的天然气水合物90%以上存在于300~ 4 000 m深的海底，目前提出的天然气水合物开采方案有降压开采法、热激发开采法、化学试剂注入开采法、二氧化碳置换法和固态开采法等[4−6]。天然气水合物绞吸式开采方案[7]是结合开采深海锰结核和绞吸式挖泥船提出的一种新的天然气水合物固态开采方案，天然气水合物在海底经采矿车绞刀破碎后再通过垂直硬管输送至海面分解。其中，使用管道将天然气水合物运输到海面是该方案的关键环节之一，天然气水合物在输送到某一高度达到其分解温压条件时会分解出气体，所以，天然气水合物管道输送可以分为临界分解面以下的固液两相流输送和分解面以上的固液气三相流输送[8]。对于固液两相输送，CHRISTIAN等[9]研究了铁精矿长距离管道输送过程中输送参数变化对能量利用率的影响；VÁCLAV等[10]结合已有管道浆体摩擦压降模型给出了水平流中有固定床的管道浆体输送摩擦压降的半经验公式，并通过实验验证了公式的有效性；VAN WIJK[11]等结合流化理论对垂直水力输送系统稳定性进行理论分析和实验验证，证明了该理论的预测结果在一定条件下符合实际情况；黄中华等[12]采用理论分析和数值计算相结合的方法分析了多金属硫化物颗粒垂直管道水力提升规律；邱灏等[13]结合不同学者对粗颗粒输送的实验结果，提出了粗颗粒在管道输送中不淤临界流速的计算式；赵国景等[14]通过理论分析得出动态管道内压力损失大于静态管道内压力损失，并通过仿真分析得到了动态管道内颗粒碰撞情况；唐达生等[15]通过理论分析和实验结合的方法得到了锰结核、富钴结壳、多金属硫化物和模拟结核的单颗粒以及非均匀颗粒群浮游速度的半经验半理论公式。研究者对固液两相流的研究大多涉及沉降速度、临界速度和输送参数对输送系统流态及稳定性的影响，研究对象多为泥沙颗粒和金属结核等，而对于天然气水合物输送过程中系统参数变化对系统压力损失的影响规律的研究较少。为此，本文作者以稳态条件下天然气水合物垂直输送管道为研究对象，结合原有浆体输送理论，运用计算流体力学和Fluent流体计算仿真软件对天然气水合物输送过程进行仿真分析，得到输送管径、浆体流速、颗粒粒径和体积分数变化对输送系统压力损失的影响规律，以便为实际天然气水合物输送系统设计确定合理的参数范围。

1 数值模拟基础

1.1 计算模型及网格划分

对比分析5，10和20 m长三维全流道管道模型的仿真计算结果，其中，10 m和20 m长模型仿真计算结果基本相同，且与5 m长模型结果相差较大，最后选择10 m长管道模型作为研究对象。管道模型三维结构网格如图1所示。借助ICEM网格划分工具，采用结构化网格对管道模型进行网格划分，网格数量为250万个，继续加密网格计算误差均小于1.8%，满足计算精度和时间要求。

图1 管道模型三维结构网格

1.2 数学模型

天然气水合物管道水力输送系统中固相颗粒粒径大于10 mm，体积分数大于10%，属于大颗粒高体积分数固液两相流分析，且固相颗粒在整个流体中都有分布，两相之间存在强烈的相互作用，所以，选择Fluent中的Eulerian模型。不考虑温度影响，输送管道内固液两相流动的控制方程包括质量守恒方程、动量守恒方程和湍流方程[16−18]。

1.2.1 液相控制方程

连续方程为

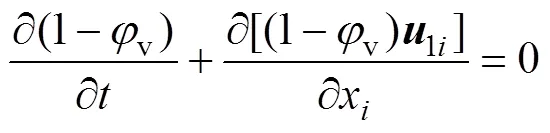
动量方程为

(2)

输送管道内流体液相采用Fluent提供的标准−ε模型，采用该模型可以得到流动的详细信息，适合管道流体湍流流动的仿真计算。具体的湍动能和湍动耗散率的输送方程参见文献[19−20]。

1.2.2 固相控制方程

连续方程为

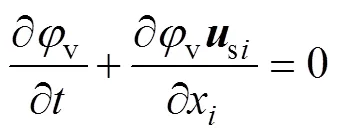
动量方程为

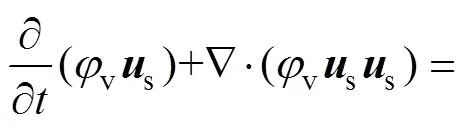
式中：s为液相速度矢量；s为固相密度；s为固相受到的应力张量；s为固相单位质量外力；s为相间作用力。

1.3 边界条件

1) 固相平均密度[21]：天然气水合物密度为 930 kg/m3，海底沉积物密度为1 600~2 200 kg/m3。按照天然气水合物体积分数为30%，海底沉积物密度 2 000 kg/m3可得固相颗粒的平均密度s为 1 679 kg/m3。

2) 进口条件：定义进口边界为速度入口，设定进口速度和固相浓度，速度方向沿管道轴线方向，定义湍流强度和水力直径。

3) 出口条件：选用压力出口，定义出口压力、湍流强度和水力直径。

4) 壁面：采用无滑移固定壁面边界。

2 输送系统压力损失的计算分析

输送管道直径、浆体流速、颗粒粒径和固相体积分数对天然气水合物输送系统压力损失有直接影响，系统压力损失直接决定主泵的选型。研究上述参数变化对输送系统压力损失的影响，对于输送系统设计和入口流体特性参数的确定都有重要意义。采用控制变量法依次改变上述4个参数进行仿真计算，研究各参数对输送系统压力损失的影响规律，确定各参数的合理范围。

2.1 输送系统压力损失计算分析

Fluent后处理软件可以在选定的面上对压力进行积分运算，对于固液两相流体无法直接积分得出总压，但可以分别计算得到选定面上的静压及两相的动压，两者相加即可得到该面上的总压。用管道进口总压减去出口总压再除以管道的长度，即得到该段管道内的压力损失梯度，公式为

式中：Δ为压力损失梯度，Pa/m；in管道为进口总压，Pa；out为出口总压，Pa；为管道长度。

总压的计算公式为

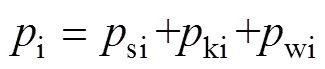
式中：i为总压，Pa；si为静压，Pa；ki为固相动压，Pa；wi为液相动压，Pa。

2.2 压力损失梯度沿输送管道轴向的变化规律

不同输送参数下压力损失沿管道轴向变化规律如图2所示。从图2可见：输送系统在4种不同的工作参数(管径、速度、颗粒粒径和固相体积分数)下，流体的压力损失梯度相差很大，但压力损失梯度沿管道轴向变化规律基本相同；在入口后4 m和出口前1 m的范围内压力损失梯度变幅较大，在4~9 m范围内压力损失梯度基本稳定。因为固相颗粒在进入管道后，由于重力原因速度会变慢，导致固相颗粒在入口处积累使固相体积分数变大，而后进来的颗粒与减速后的颗粒发生碰撞使入口处浆体流动混乱，颗粒与管壁以及颗粒与颗粒之间碰撞的概率增大，致使压力损失增大。混乱的固相在液相的推动下继续上升并趋于平稳，压力损失也慢慢降低，最终在进入管道3 m左右达到稳定状态。在到达出口时前面没有浆体流动，颗粒之间的碰撞减少，压力损失梯度稍微变小。取仿真模型中4~9 m的管段为有效工作段进行压力损失梯度计算，更加符合天然气水合物输送系统实际工况。

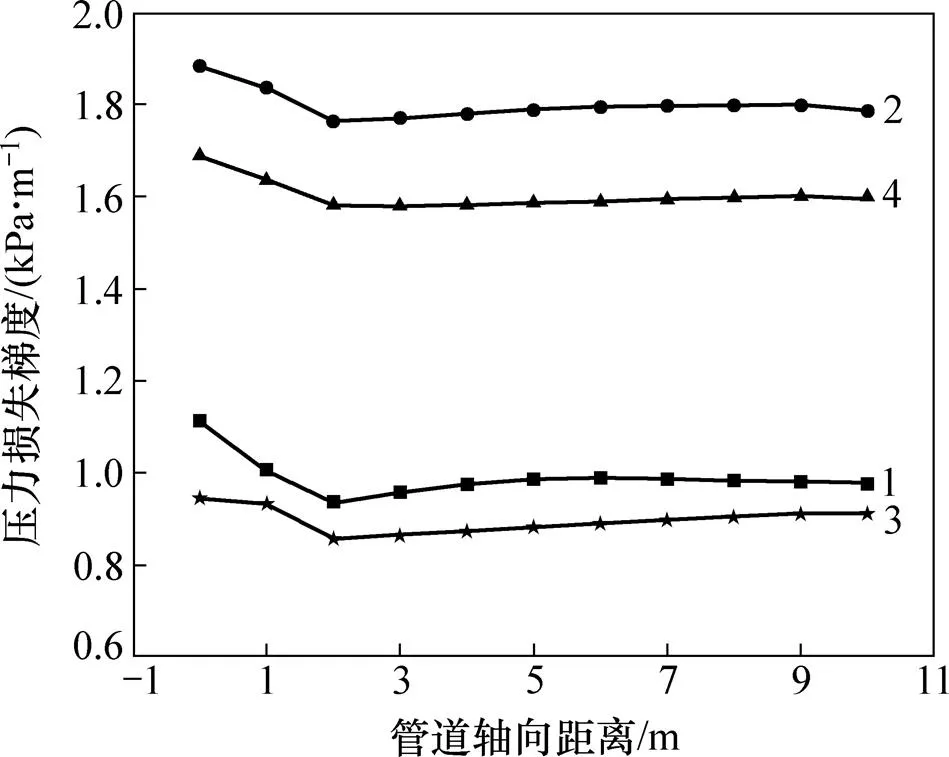
1—管径为0.15 m，速度为2.0 m/s，颗粒粒径为0.01 m，固相体积分数为10%；2—管径为0.20 m，速度为2.0 m/s，颗粒粒径为0.02 m，固相体积分数为20%；3—管径为0.30 m，速度为3.0 m/s，颗粒粒径为0.01 m，固相体积分数为10%；4—管径为0.40 m，速度为3.0 m/s，颗粒粒径为0.15 m，固相体积分数为20%。

2.3 管道直径对压力损失的影响

输送系统管道直径在系统设计时被确定并且在工作过程中无法更改，所以，管径的选择必须慎重。设定管径变化范围为0.15~0.55 m。为了研究管径的影响规律是否具有普遍性，选择3种不同的流体入口参数(速度、颗粒粒径和固相体积分数)组合，仿真结果如图3所示。从图3可以看出：不同入口参数对应的系统压力损失梯度差别很大，但各组参数对应的压力损失梯度随管道直径的变化规律相同，其规律表现为压力损失梯度随着管径的增加而减小，因为随着管径增大，单位体积浆体与管道的接触面积减小，相应的浆体与管道的摩擦损失及颗粒与管壁碰撞的能量损失减少；当管径增大到0.3 m以后，继续增大管径，压力损失减小量越来越少，因为管径较小时，浆体与管道的摩擦损失及颗粒与管壁碰撞的能量损失在压力损失中占比较大，随着管径增加，该部分能量损失占比越来越小，对压力损失的影响程度减弱。总体来说，天然气水合物输送系统可以通过增加输送管径的方法来减少压力损失，但当管径超过一定值以后，继续增大管径对总压损失的影响较小，初步选择管径为0.3~0.4 m。

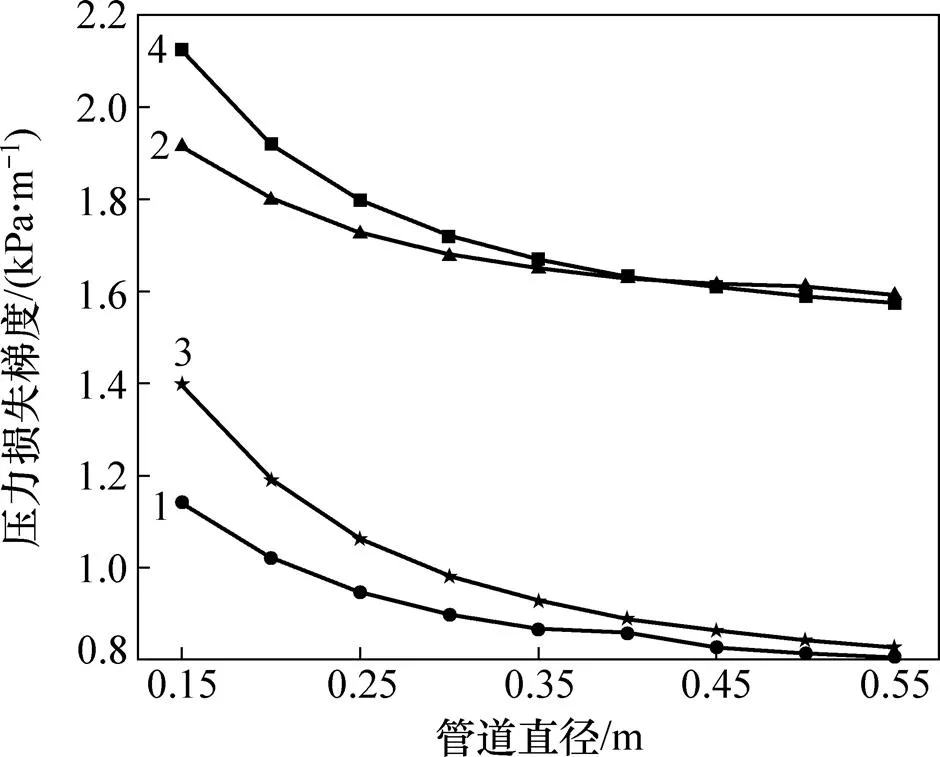
1—速度为3 m/s，颗粒粒径为0.01 m，固相体积分数为10%；2—速度为3 m/s，颗粒粒径为0.02 m，固相体积分数为20%；3—速度为4 m/s，颗粒粒径为0.01 m，固相体积分数为10%；4—速度为4 m/s，颗粒粒径为0.02 m，固相体积分数为20%。

从图3还可以看出：当浆体速度相同而颗粒粒径和固相体积分数不同时，系统压力损失梯度之间的差值为30%~50%；当浆体速度不同而颗粒粒径和固相体积分数相同时，系统压力损失梯度之间的差值小于20%，这说明颗粒粒径或固相体积分数对输送系统压力损失的影响要比浆体速度的影响大；当管径大于0.4 m且颗粒粒径和固相体积分数相同时，输送系统在不同浆体速度下的的压力损失梯度相差很小，这是由于管径增大导致浆体与管道的摩擦损失及颗粒与管壁碰撞的能量损失在压力损失中占比减小。

2.4 浆体流速对压力损失的影响

选择管道直径为0.35 m，固相颗粒粒径和固相体积分数组合如下：颗粒粒径为0.01 m，体积分数为10%；颗粒粒径为0.02 m，体积分数为20%；颗粒粒径为0.03 m，体积分数为30%。研究这3种不同工况下浆体速度在2.0~6.0 m/s之间变化时压力损失梯度的变化规律，仿真结果如图4所示。从图4可见：在这3种不同粒径和体积分数的组合下，压力损失梯度的差值很大，说明颗粒粒径或者体积分数对系统压力损失的影响很大；在这3种工况下，浆体速度对压力损失梯度的影响规律相似，随着浆体速度增大，压力损失梯度先减小后增大，即存在1个最优流速；当浆体速度在最优流速附近变化时，压力损失梯度变化较小；当速度增大或减小到一定值后，压力损失梯度与速度呈指数变化的关系。这是因为固体颗粒进入管道后由于重力作用速度会减小，固相与液相之间会出现滑移，浆体速度越小，滑移速度越大，滑移使固相出现累积而使固相体积分数增大，导致颗粒与颗粒之间的碰撞和颗粒与管壁之间的碰撞增加，从而导致系统压力损失增大；增大浆体速度可以减小固液两相之间的滑移，进而使固相体积分数减小，因滑移和碰撞而产生的压力损失也随着减小；当浆体速度达到一定值时，继续增大浆体速度对固液两相之间滑移的影响很小，固相体积分数也基本保持不变，固相颗粒的高速流动反而导致颗粒与颗粒以及颗粒和管径之间的碰撞大量增加，所以，压力损失又会呈现快速增大的现象，即压力损失梯度随浆体速度的变化是固液两相之间的滑移所致。

压力损失梯度随浆体速度的增加先减小后增大，达到最小值时对应的浆体速度称为最佳速度。从图4还可以看出：随着颗粒粒径和固相体积分数增大，最佳速度也增大，3组工况对应的最佳速度分别为2.5，3.0和3.5 m/s。这是因为颗粒粒径越大，固液两相之间的滑移越大，要使两相之间的滑移达到稳定就需要更大的浆体速度。在实际开采中，如何选择浆体流速要根据矿石颗粒粒径来确定，合理的浆体速度范围为2.5~4.0 m/s，速度大就需要系统提供更大的功率，而相应的压力损失也会增大。

2.5 固相体积分数对压力损失的影响

选择管道直径为0.35 m，浆体流速为3.5 m/s，仿真计算固相颗粒粒径分别为0.01，0.03和0.05 m时，输送系统压力损失梯度随固相体积分数的变化规律，其中固相体积分数为8%~32%，仿真结果如图5所示。从图5可见：在同一体积分数下，固相颗粒粒径越大，系统压力损失就越大。这是因为颗粒粒径越大，固相与液相之间的相对滑移就越大，固液两相之间滑移产生的压力损失也就越大。

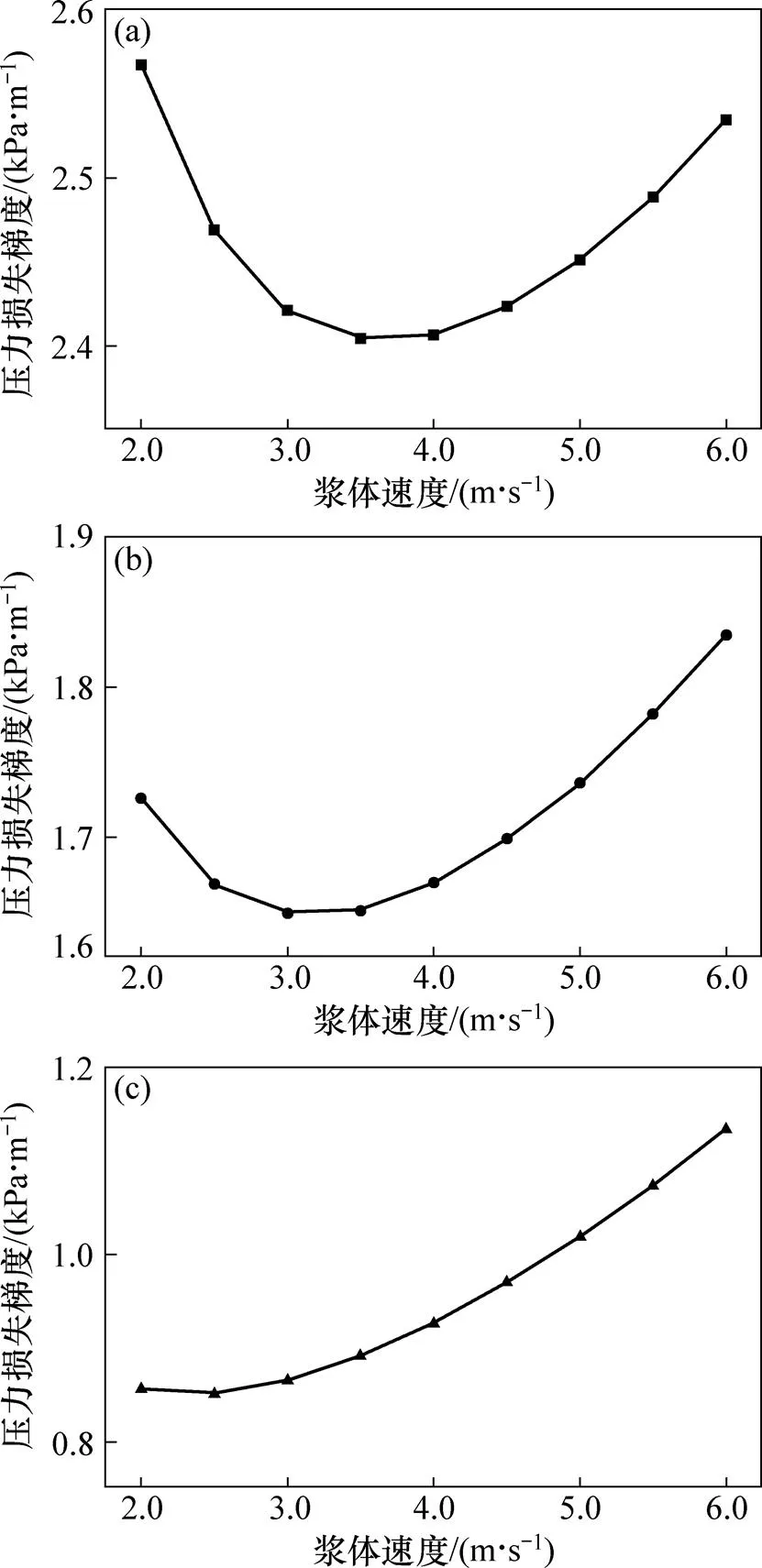
(a) 颗粒粒径为0.03 m，固相体积分数为30%； (b) 颗粒粒径为0.02 m，固相体积分数为20%； (c) 颗粒粒径为0.01 m，固相体积分数为10%

Fig. 4 Influence of slurry speed on pressure loss gradient at different particle sizes and volume fraction

在3种颗粒粒径条件下，压力损失梯度随固相体积分数的变化规律完全相同：随着固相体积分数增大，压力损失梯度呈线性增加，固相体积分数增大1%，压力损失梯度便增大70 Pa/m左右。一方面，固相体积分数增大使浆体密度增大，在浆体输送过程中位能损失增大；另一方面，固相体积分数增大使单位体积浆体内固相颗粒数量增加，这就导致固相颗粒之间、固相颗粒与管壁之间的碰撞次数变多，输送系统因碰撞而产生的压力损失增大。在实际生产过程中，考虑到系统功率限制，要控制输送浆体固相体积分数不能太大。固相体积分数太大容易造成堵管，而固相体积分数太小，则生产效率太低，所以，初步选定固相体积分数在15%~25%之间。

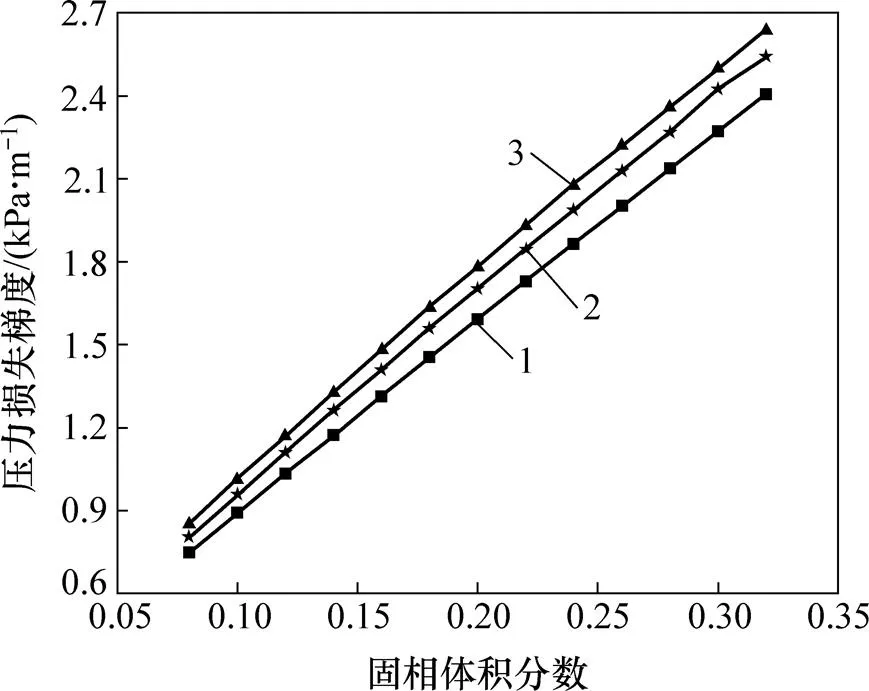
颗粒粒径/m：1—0.01；2—0.03；3—0.05。

2.6 颗粒粒径对压力损失的影响

选择管道直径为0.35 m，浆体流速为3.5 m/s，固相体积分数为20%，仿真分析颗粒粒径在0.01~0.05 m之间变化时输送系统压力损失梯度的变化规律，结果如图6所示。从图6可见：压力损失梯度随颗粒粒径的增大基本呈线性增大。其主要原因是颗粒粒径变大使固液两相之间的相对滑移增大，但增幅度不大，颗粒粒径每增大0.01 m，压力损失梯度增加50 Pa/m左右。在实际生产中，在保证不堵管的前提下，可以选择较大的颗粒粒径，这样，在采矿车对颗粒进行破碎时可使功率消耗较少。结合以上分析可知，颗粒粒径对压力损失梯度的影响较小，固相体积分数对压力损失梯度的影响较大。

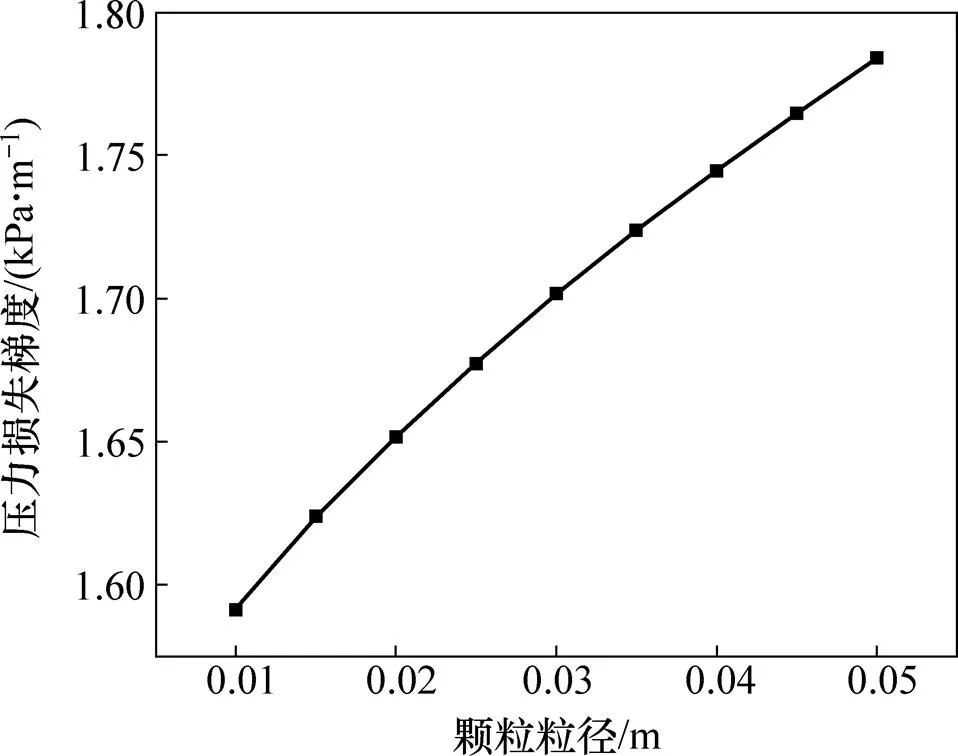
图6 颗粒粒径对压力损失梯度的影响

3 压力损失梯度计算结果与实验结果对比

中南大学机电工程学院与长沙矿冶研究院联合建立了深海矿产资源开发利用国家重点实验室，实验室在“中国大洋协会”资助下建立了高为20 m、管径为0.2 m的深海采矿扬矿试验台，可通过施加背压的方法模拟深海扬矿工况。为验证仿真结果的正确性，以模拟矿石(密度1 700 kg/m3)为实验对象，通过该试验台测量输送管道直径为0.2 m时不同浆体输送参数压力损失梯度。实验与仿真结果如表1所示。从表1可见：压力损失梯度实验结果普遍比仿真结果大，因为实验所用矿石比仿真所用矿石固相密度大，两者之间的相对误差在7.2%以内，表明仿真结果精度较高。

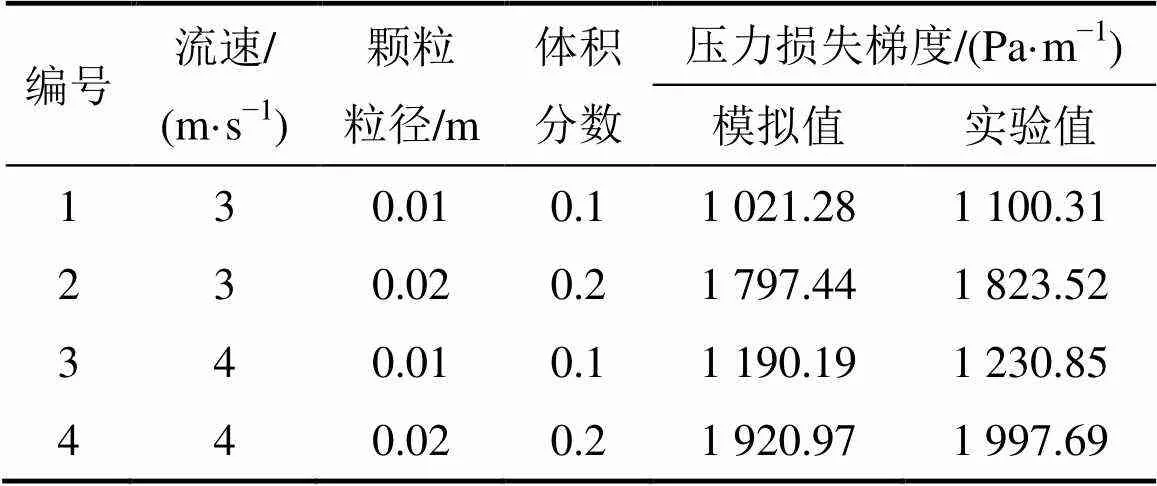
表1 压力损失梯度模拟值与实验值对比

4 结论

1) 压力损失梯度随着输送管道直径的增大而减小，当直径增加到0.4 m时，继续增大管道直径，对压力损失的影响较小，初步选定输送系统管道设计直径在0.3~0.4 m之间。

2) 随着浆体流速增大，压力损失梯度先减小后增大，存在1个最优流速，流速在最优流速附近变化时，压力损失梯度变化较小；当流速和最优流速相差较大时，压力损失梯度和流速呈指数变化关系；对于不同粒径的颗粒，输送最优流速也不同，颗粒粒径越大，最优流速也越大，基本保持在2.5~4.0 m/s之间。

3) 压力损失梯度随固相体积分数的增大呈线性增大，体积分数增加1%，压力损失梯度增加70 Pa/m左右，在实际生产中，建议选择体积分数在15%~25%之间。

4) 压力损失梯度随颗粒粒径增大呈线性增大，但是变化幅度较小，颗粒粒径每增大0.01 m，压力损失梯度增加50 Pa/m左右。

5) 在天然气水合物管道输送过程中，固相体积分数对压力损失梯度的影响较大，浆体流速和管道直径的影响次之，颗粒粒径的影响最小。

6) 实验测得的输送管道压力损失梯度与仿真结果相对误差在7.2%以内，表明仿真结果精度较高。

[1] MAKOGON Y F. Natural gas hydrates-a promising source of energy[J]. Journal of Natural Gas Science and Engineering, 2010, 2(1): 49−59.

[2] RAJNAUTH J, BARRUFET M. Monetizing gas:focusing on developments in gas hydrate as a mode of transportation[J]. Energy Science and Technology, 2012, 4(2): 61−68.

[3] MOHEBBI V, BEHBAHANI R M. Experimental study on gas hydrate formation from natural gas mixture[J]. Journal of Natural Gas Science & Engineering, 2014, 18: 47−52.

[4] 吴传芝, 赵克斌, 孙长青, 等. 天然气水合物开采研究现状[J]. 地质科技情报, 2008, 27(1): 47−51. WU Chuanzhi, ZHAO Kebin, SUN Changqing, et al. Current research in natural gas hydrate production[J]. Geological Science and Technology Information, 2008, 27(1): 47−51.

[5] 刘建军, 邵祖亮, 郑永香. 天然气水合物降压分解过程的数值模拟[J]. 西南石油大学学报(自然科学版), 2017, 39(1): 80−90. LIU Jianjun, SHAO Zuliang, ZHENG Yongxiang. Numerical Simulation of the Decomposition of Natural Gas Hydrates by Depressurization[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2017, 39(1): 80−90.

[6] 徐纯刚, 李小森, 蔡晶, 等. 二氧化碳置换法模拟开采天然气水合物的研究进展[J]. 化工学报, 2013, 64(7): 2309−2315. XU Chungang, LI Xiaosen, CAI Jin, et al. Advance on simulation exploitation of natural gas hydrate by replacement with CO2[J]. Journal of Chemical Industry and Engineering. 2013, 64(7): 2309−2315.

[7] 徐海良, 林良程, 吴万荣, 等. 海底天然气水合物绞吸式开采方法研究[J]. 中山大学学报(自然科学版), 2011, 50(3): 48−52. XU Hailiang, LIN Liangcheng, WU Wanrong, et al. Cutter-suction Exploitation Mode of Marine Gas Hydrate[J]. Transactions of the British Mycological Society, 2011, 50(3): 48−52.

[8] 徐海良, 孔维阳, 杨放琼. 天然气水合物在水力提升管道中的分解特性[J]. 天然气工业, 2018, 38(7): 129−137. XU Hailiang, KONG Weiyang, YANG Fangqiong. Decomposition characteristics of natural gas hydrates in hydraulic lifting pipelines[J]. Natural Gas Industry, 2018, 38(7): 129−137.

[9] CHRISTIAN F I, SANTIAGO M S, ALDO T B. A cost perspective for long distance ore pipeline water and energy utilization. Part II: effect of input parameter variability[J]. International Journal of Mineral Processing, 2013, 122(122): 54−58.

[10] VÁCLAV M. Predictive model for frictional pressure drop in settling-slurry pipe with stationary deposit[J]. Powder Technology, 2009, 192(3): 367−374.

[11] VAN WIJK J M, TALMON A M, VAN RHEE C. Stability of vertical hydraulic transport processes for deep ocean mining:an experimental study[J]. Ocean Engineering, 2016, 125: 203−213.

[12] 黄中华, 曹跃, 谢雅. 多金属硫化物颗粒水力提升性能仿真[J]. 机械设计与研究, 2015, 31(2): 85−88. HUANG Zhonghua, CAO Yue, XIE Ya. Simulation of hydraulic lifting performance of polymetallic sulfide particles[J]. Machine Design and Research, 2015, 31(2): 85−88.

[13] 邱灏, 曹斌, 夏建新. 粗颗粒物料管道水力输送不淤临界流速计算[J]. 水利水运工程学报, 2016(6): 103−108. QIU Hao, CAO Bin, XIA Jianxin. Non-silting critical velocity calculation of coarse-grained materials in hydraulic pipeline[J]. Hydro-Science and Engineering, 2016(6): 103−108.

[14] 赵国景, 夏建新, 黄家桢. 锰结核动态管道水力提升[J]. 矿冶工程, 2000, 20(3): 18−24. ZHAO Guojing, XIA Jianxin, HUANG Jiazhen. Hydraulic lifting of dynamic pipeline for manganese nodules[J]. Mining and Metallurgical Engineering, 2000, 20(3): 18−24.

[15] 唐达生, 肖红, 宋跃文, 等. 深海粗颗粒矿石浮游速度的试验研究[J]. 矿冶工程, 2016, 36(3): 1−8. TANG Dasheng, XIAO Hong, SONG Yuewen, et al. Experimental study on floating velocity of coarse ore particles in deep sea[J]. Mining and Metallurgical Engineering, 2016, 36(3): 1−8.

[16] 李万, 钱忠东, 郜元勇. 4种湍流模型对混流式水轮机压力脉动模拟的比较[J]. 武汉大学学报(工学版), 2013, 46(2): 174−179. LI Wan, QIAN Zhongdong, GAO Yuanyong. Comparison of pressure oscillation characteristics in a Francis hydraulic turbine with four different turbulence models[J]. Engineering Journal of Wuhan University, 2013, 46(2): 174−179.

[17] 徐海良, 周刚, 吴万荣, 等. 深海采矿储料罐输送设备固液两相流数值计算与分析[J]. 中南大学学报(自然科学版), 2012, 43(1): 111−117. XU Hailiang, ZHOU Gang, WU Wanrong, et al. Numerical calculation and analysis of solid-liquid two-phase flow intank transporting equipment for deep-sea mining[J]. Journal of Central South University(Science and Technology), 2012, 43(1): 111−117.

[18] 喻黎明, 邹小艳, 谭弘, 等. 基于CFD-DEM耦合的水力旋流器水沙运动三维数值模拟[J]. 农业机械学报, 2016, 47(1): 126−132. YU Liming, ZOU Xiaoyan, TAN Hong, et al. 3D numerical simulation of water and sediment flow inhydrocyclone based on coupled CFD-DEM[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(1): 126−132.

[19] 李秋龙. 赤泥沉降槽内多相流动和絮凝沉降的数值仿真与优化[D]. 长沙: 中南大学能源科学与工程学院, 2014: 26−27. LI Qiulong. Numerical simulation and optimization on multiphase flow and flocculation, sedimentation in the red mud thickener[D]. Changsha: Central South University. School of Energy Science and Engineering, 2014: 26−27.

[20] QI Nana, ZHANG Hu, ZHANG Kai, et al. CFD simulation of particle suspension in a stirred tank[J]. Particuology, 2013, 11(3): 317−326.

[21] 徐海良, 陈旺, 吴波, 等. 海底天然气水合物绞吸式开采切削头绞吸特性[J]. 四川大学学报(工程科学版), 2016, 48(6): 126−131. XU Hailiang, CHEN Wang, WU Bo, et al. Characteristic of Cutting Head in Marine Gas Hydrate by Cutter Suction Exploitation[J]. Journal of Sichuan University(Engineering Science Edition) , 2016, 48(6): 126−131.

Pressure loss of conveying pipeline of natural gas hydrate

XU Hailiang1, 2, HU Wengang1, YANG Fangqiong1, 2

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China; 2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

To study the influence law between pressure loss of conveyor system and parameters of hydraulic transmission system for cutter-suction mining in submarine natural gas hydrate exploitation, such as diameter, velocity, volume fraction and particle size, and to determine the reasonable selection of the parameters, the three-dimensional flow field model of pipeline was established, and the method of controlling variables, the computational fluid dynamics theory and Fluent simulation software were used for numerical analysis in the solid liquid two-phase flow field of the pipeline. The results show that the pressure loss gradient of the conveying system decreases with the increase of the pipe diameter, and when the diameter of the pipe increases to 0.4 m, the effect of increasing the pipe diameter on pressure loss gradient is smaller and smaller. The pressure loss gradient decreases first and then increases with the increase of the flow velocity of the slurry, and there is an optimal velocity, which is between 2.5 m/s and 4.0 m/s, and the larger the particle size and volume fraction, the greater the corresponding optimal velocity. The pressure loss gradient increases linearly with the increase of volume fraction. The pressure loss gradient increases with the increase of particle size, but the increase is small.

gas hydrates; hydraulic transmission; pressure loss; simulation

10.11817/j.issn.1672−7207.2019.02.008

P744；TD807

A

1672−7207(2019)02−0304−07

2018−03−12；

2018−05−22

国家自然科学基金资助项目(51775561)(Project(51775561) supported by the National Natural Science Foundation of China)

杨放琼，博士，教授，从事深海采矿研究；E-mail：376212096@qq.com

(编辑 陈灿华)