地形起伏地区平面坐标转换方法及精度分析

马海英，胡月明，姚朝龙，范亚南,，胡碧霞，张 伟

(1. 德令哈市国土资源局，青海 德令哈 817000； 2. 华南农业大学资源环境学院，广东 广州 510642；3. 国土资源部建设用地再开发重点实验室，广东 广州 510642； 4. 广东省土地利用与整治重点实验室，广东 广州 510642； 5. 广东省土地信息工程技术研究中心，广东 广州 510642； 6. 青海大学农牧学院,青海 西宁 810016； 7. 广州市华南自然资源科学技术研究院,广东 广州 510642； 8. 青海友元空间信息技术有限公司，青海 西宁 810008)

随着测绘理论和技术的发展，我国在不同时期建立了不同的坐标系，包括1954北京坐标系、1980西安坐标系、2000国家大地坐标系。为了统一使用不同坐标系下的成果，通常需要进行坐标转换。坐标转换方法包括直接进行三维坐标转换[1]，以及通过平面坐标转换[2]和高程拟合[3]来达到三维坐标的转换。平面坐标转换的主要方法有四参数模型[4-5]、多项式转换模型[6]、格网插值[7]等，模型参数解算方法有最小二乘法[8]、总体最小二乘法[8-10]等。

坐标转换的精度不仅受转换模型的影响，还与公共点个数和分布、地形情况等因素有关。对于小范围平坦地区，各模型的转换精度都较高，而且差异不大[11]。即使在地形起伏较大的小范围地区，各模型的转换精度也能达到厘米级，能够满足普通工程应用的要求[12-13]。而对于地形起伏较大的大范围区域，坐标转换的精度受不同因素的影响较大。本文将探讨四参数模型和二次曲面模型在地形起伏较大地区的适用性，以及公共点选取对模型转换精度的影响。

1 坐标转换模型

1.1 四参数模型

四参数模型[5,14]是一种相似变换，其计算公式为

(1)

式中，Δx、Δy、θ、m分别为平面上的平移、旋转、尺度参数。当有两个以上转换公共点时，将此模型转换为线性模型用最小二乘求解，即

(2)

1.2 二次曲面模型

二次多项式拟合[6,15]是多项式变换中的一种，其计算公式为

(3)

式中，a0、a1、a2、a3、a4、a5、b0、b1、b2、b3、b4、b5为转换参数，当转换点个数大于6时，可以通过最小二乘法结合线性回归原理求解转换参数。

1.3 精度评定

转换残差计算公式为：vx=x′-x，vy=y′-y。其中x′、y′为转换后坐标值，x、y为同名点原坐标值。

坐标分量X、Y转换中误差为

计算内符合精度时，n为转换点个数；计算外符合精度时，n为检验点个数。

点位中误差为

2 试验区和数据

青海高原地形起伏大，矿山分布较为零散，本文采用的矿业权核查坐标数据范围大，面积约为4000 km2，共有9个公共点，其中A02和A04的距离最远，约为108 km。图1为公共点分布和地形起伏情况。地势西低东高，海拔最低为3113 m(A08)，最高为4261 m(A02)，公共点最大高差达1148 m，而且受矿山分布的影响，公共点分布也不均。

3 试验结果与讨论

3.1 两种模型比较

虽然四参数模型只需要2个公共点即可求解转换参数，但由于二次曲面模型参数的求解至少需要6个公共点，因此，本文采用3种公共点组合方案对比四参数模型和二次曲面模型的适用性(见表1)，其他公共点作为检验点，检验坐标转换的外符合精度。

表1 3种公共点组合方案

在组合1的方案中，公共点主要选取的是测区的边界点(图2中圆圈点)，表2显示四参数的X、Y分量的内外符合精度在分米至米级(点位中误差分别为1.362 m和1.262 m)，最小绝对偏差为0.136 m(A07)，最大绝对误差达到了1.697 m(A04)。这样的转换精度显然无法满足高精度工程应用的需要。而二次曲面模型的外符合转换精度则要高很多，精度为厘米级(点位中误差为6.8 cm)，外符合最大绝对偏差为7.6 cm(A05)。由于6个公共点刚好求解二次曲面模型的转换参数，没有多余观测值，因此其内符合转换误差为0。

组合2的方案将区域内部的A05号点纳入转换点中，四参数模型坐标转换的最小绝对偏差减少至9.1 cm(A07)，但是最大绝对偏差却增加至1.759 m(A04)，内外符合的点位中误差分别为1.291 m和1.476 m。二次曲面模型的外符合精度中最大最小绝对偏差几乎没有变化，但坐标转换的整体精度有所提高，外符合点位中误差减小至5.5 cm。

组合3的方案将测区内最低点A08(3113 m)纳入到转换点中，四参数模型坐标转换的外符合精度反而明显降低，点位中误差达2.024 m。这说明对于大范围区域，四参数模型进行坐标转换的精度不仅受公共点数量和分布的影响，而且地形因素对其也有着明显的影响。但二次曲面模型的坐标转换精度，无论是最大绝对偏差还是整体的点位中误差都有较为明显的减小。因为用于求解坐标转换参数的公共点越多，二次曲面模型越能反映测区坐标的差异特征。

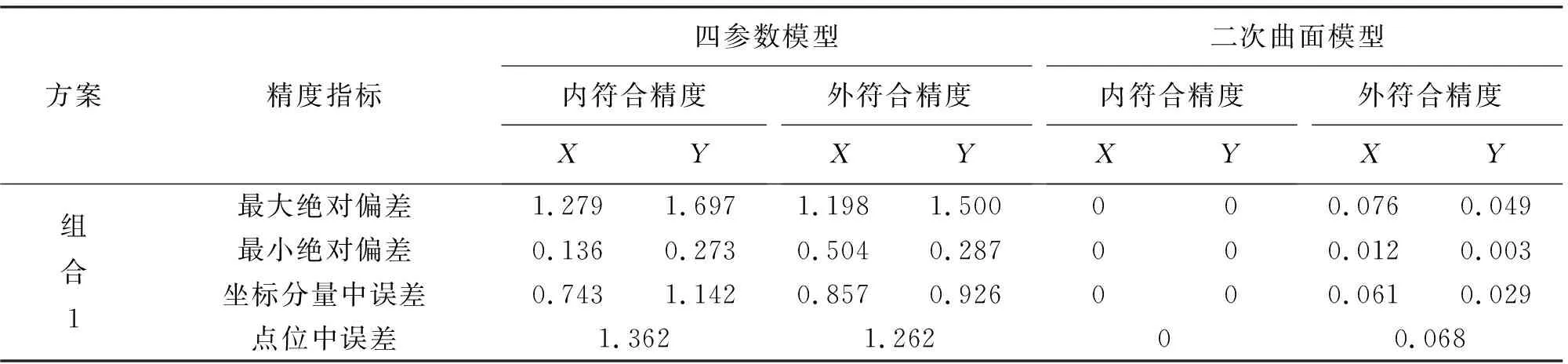
表2 不同组合方案两种模型的坐标转换精度统计 m

续表2 m

3.2 二次曲面模型分析

由以上分析可知，二次曲面模型在地形起伏较大的地区适用性更强。为了进一步分析该模型的外推能力，选取不同的公共点进行试验。图3(a)和(b)中选取西南角6个公共点点作为转换点，东北角的A01、A02和A05作为检验点进行坐标转换。从图中可以看出，检验点的转换精度很差，X分量的误差超过10 m。由此可见，对于地形起伏大的大范围区域，二次曲面模型的外推能力很弱。图3(c)和(d)进一步将最远、最高的A02纳入转换点中，检验点坐标转换精度有了明显的提高，处于区域内部的A05号点的转换精度有了明显提高，最大偏差为-0.700 m，而处于区域外部的A01号点的最大误差达到-3.083 m，仍无法用于高精度的工程应用中。这说明将区域边界的点纳入转换点可以明显改善区域内部坐标转换的精度，但区域外部的转换精度仍较差。图3(e)和(f)进一步将区域边界的A01号点纳入转换点中，坐标转换的内外符合精度均达到了厘米级的精度，最大偏差为7.8 cm。

4 结 论

本文研究了地形起伏大的大范围区域两种平面坐标转换模型的适用性。研究结果表明：

(1) 四参数模型的坐标转换精度在分米至米级，无法满足高精度的工程应用需求。受地形因素的影响，纳入更多公共点作为转换点时反而可能会降低坐标转换的精度。

(2) 当合理选择转换点时，二次曲面模型的坐标转换精度为厘米级，而且增加转换点的数量可以增加坐标转换的精度。然而，由于地形起伏较大，该模型的外推能力也很差，因此，通常要选取测区边界的公共点作为转换点才能得到较高的坐标转换精度。