基于MATLAB的轮毂电机驱动电动汽车的平顺性研究

张丽萍，李勇凯，李争鹏

（辽宁工业大学汽车与交通工程学院，辽宁 锦州 121001）

引言

随着世界范围内汽车保有量不断增加和工业生产的迅速发展，资源消耗和空气污染等问题日益严重，未来大力发展新型能源汽车是解决环境污染与能源危机的有效方法[1]。电动汽车以其如下优点而备受重视，车辆在使用过程中零污染（或超低污染）、能源利用更加多元高效，以及有利于实现智能化控制等多方面的技术优势。当前新能源汽车在世界范围内呈现加速发展态势。按照车辆提供驱动力的方式不同，可以将电动汽车大体上分为两类，即集中电机驱动和轮毂电机驱动电动汽车。轮毂电机驱动相比于集中电机驱动电动汽车布局更加合理、空间利用充分、能量便于回收等特点，轮毂电机驱动技术具有很好的发展和实际应用前景[2]。作为电动汽车未来技术发展的一个重要方向，轮毂电机驱动技术是当前国内外发展研究的重点和热点之一。由于新型的驱动形式和特殊的结构布局，加剧了车辆的垂向振动，导致了车辆的平顺性和操纵稳定性变差。本文轮毂电机选择开关磁阻电机，主要从非黄载质量增加和电机运转时产生的转矩波动两个方面对车辆垂向振动的影响进行研究[3]。

1 路面输入模型

轮毂电机驱动电动汽车行驶时，路面输入是系统的主要激励，对电动汽车进行平顺性分析时，首先研究路面输入。采用功率谱密度法，推导路面输入的时域模型，国际上常采用式（1）来表示路面功率谱密度Gq(n)：

式中n为空间频率；n0=0.1m-1为参考空间频率；w为频率指数，通常w=2；Gq(n0)为路面不平度系数。f为时间频率，u为车速。路面等级分为八个等级，B、C级路面在城市中较为常见。采用理想单位白噪声输入，为了更准群的得反映路面的实际情况，我们引入下截止频率（n00,取0.01）式（1）、式（2）、式（3）经过推导变换可以得出路面输入的时域表达式为：

q(t)—路面随机不平度位移；w(t)—均值为0和功率谱密度是1的高斯白噪声[4]在Simulink中建立单轮随机路面输入仿真模型如图1所示。

图1 单轮随机路面输入仿真模型

针对轮毂电机驱动电动汽车行驶路况的大致情况，本文选用路面不平度8级分类中的B级路面进行研究，B级路面的不平度系数为，车速取为30km/h，仿真可得B级路面输入谱，如图2所示。

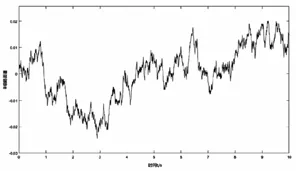
图2 B级路面输入谱

2 轮毂电机驱动电动汽车1/4汽车模型

选择8/6极开关磁阻电机作为轮毂电机，电机激励F(t)是由轮毂电机运转时由于转矩波动产生的，它是由电机的切向力和径向力在竖直方向的分力两部分组成[5]，如图3所示。

图3 电机径向力、切向力在竖直方向的合力

轮毂电机的径向力和切向力经过一系列的推到变换，得到电机激励F(t)的等式：

这里b为极对极时气隙长度lg的最短距离；转子半径r=R-b，φ为转子初相角，通过控制各相绕组的接通与断开顺序来控制电机的旋转方向，通过控制绕组中电流的大小和开通和断开角度来控制电动机的转速，进而影响电机激励的大小。具体参数如表1所示：

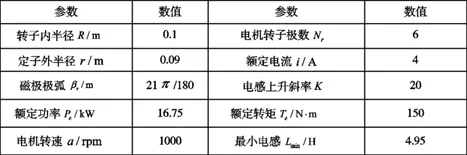
表1 四相8/6极开关磁阻电机参数

仿真模型搭建过程：依据电机激励F(t)的方程式在Matlab中进行编程，应用plot函数得电机激振力在时间域内的图像，如图4所示。

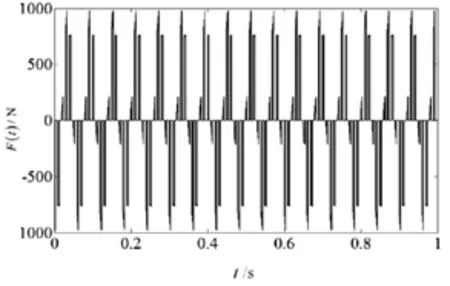
图4 电机激励F(t)

在假设悬挂质量分配系数ε=1，轮毂电机驱动电动汽车实际结构左右对称且左右车辙的不平度函数相等的情况下，轮毂电机驱动电动汽车简化为四分之一车两自由度振动系统，如图所示。此系统较集中驱动系统增加了电机激励F(t)，即系统含两个输入：路面输入q、电机激励F(t)；两个输出：车轮位移z1，车身位移z2。

图5 四分之一轮毂电机驱动电动汽车的二自由度模型

对图5所示的振动系统模型，应用拉格朗日方程，得到系统的运动方程为：

车辆具体参数如表2，为单轮1/4车辆参数。

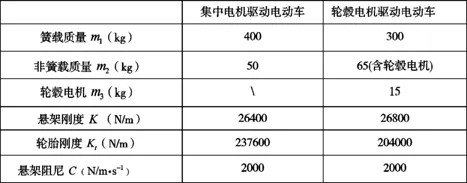
表2 单轮1/4车辆参数表

将路面激励和电机激励一同作用下的输入作为振动系统的激励，建立相对应的四分之一轮毂电机驱动电动汽车的二自由度simulink模型。如图5所示。

图5 ‘路面+电机’双激励下时域仿真Simulink模型

3 轮毂电机对垂向振动的影响

对于轮毂电机驱动电动汽车，其垂向振动的来源除了不平路面的输入激励外，还有来自轮毂电机因转矩波动产生的电机垂向激振力。因为轮毂电机的引入使得非簧载质量增加，加剧了车辆的垂向振动，导致了车辆平顺性变差。作为系统参数，非簧载质量的变动会影响振动系统的频率响应特性。通过将轮毂电机驱动电动车与集中电机驱动电动车进行频域对比分析，说明非簧载质量变大对车辆垂向振动的影响。和应用线性叠加原理，分析振动系统在时间域内路面和电机双激励情况下的响应情况。

3.1 振动系统响应特性对比分析

集中电机驱动电动汽车非簧载质量包括车轮、转向机构、制动机构和悬架杆系等部分，而对于轮毂电机驱动电动汽车，这部分质量还包含轮毂电机质量。采用集中驱动电动汽车和轮毂电机驱动电动汽车作为对比，假定簧载质量相同，研究电动汽车因引入轮毂电机而使非簧载质量增加，对车辆垂向振动的影响。

图6为集中电机驱动四分之一车模型。图中，m2+m3为簧载质量（车身质量+驱动电机质量）；m1为非簧载质量（车轮质量）；K为弹簧刚度；C为阻尼系数；Kt为轮胎刚度。

图6 四分之一集中电机驱动电动汽车的二自由度模型

其运动方程为：

自由振动即无阻尼时，方程变为：

1/4车双质量振动系统的固有频率表达式如下[6]：

由上述公式可以得出低频共振的车身型振动和高频共振的车轮型振动。

3.1.1 系统传递特性和幅频特性

将有关各复振幅代入式（7），处理得系统各传递函数：

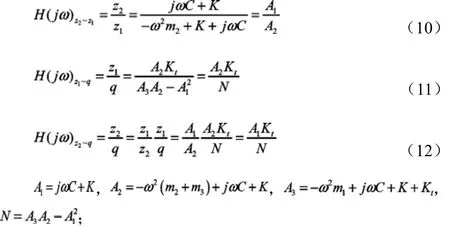
传递函数分子分母分别进行复数运算，然后求模，得幅频特性：

代入式（12），得：

（2）相对动载Fd/G对的幅频特性：

（3）悬架动挠度fd对的幅频特性：

在参考车速u=30km/h，以B级随机路面为路面激励得情况下，用Matlab进行仿真分析对比，得到系统幅频特性。经Matlab程序处理可得，车身、车轮部分固有频率分别为表3所示：

表3 车身、车轮部分固有频率

下图7、图8、图9分别为轮毂电机电动车和集中驱动电动车的幅频特性曲线图。

由图7、图8、图9的车身加速度、悬架动挠度和车轮相对动载的幅频特性图可以看出，双质量系统幅频特性曲线出现两个共振峰，在f=f0的低频共振区，轮毂电机驱动车辆的幅频特性与集中驱动电动汽车的幅频特性曲线大致重合，二者无明显差异；而在f=ft高频共振区，二者幅频特性出现明显差异，由于轮毂电机驱动车辆车轮固有频率ft比集中驱动电动车低，所以较先达到高频共振峰值，随后幅频特性以较大斜率明显衰减。并且集中驱动电动汽车的高频峰值低于轮毂电机驱动车辆，也就是说，轮毂电机驱动系统因为轮毂电机的引入而使非簧载质量增加造成平顺性变差，车身加速度增大则乘员舒适度差，悬架动挠度过大会增加撞击限位块的几率，影响行驶品质，而车轮相对动载相对路面上输入速度的幅频特性过大则影响轮胎与地面的接地性从而影响操纵稳定性，进而危及行车安全。

图7 车身加速度对速度输入 的幅频特性

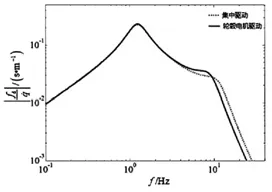
图8 悬架动挠度fd对速度输入 的幅频特性

图9 车轮相对动载fd/G对速度输入 的幅频特性

3.2 路面激励+电机激励共同作用下的系统响应

根据图所建路面+电机双重激励Simulink仿真模型，对该系统进行仿真，模拟车辆以u=30km/h的车速通过B级随机路面，得到振动系统在时间历程内的响应特性，通过只加随机路面输入作为激励和加入路面+电机垂向激振力作为激励进行对比，仿真结果数据如表4所示。

表4 轮毂电机的引入后振动系统响应均方根值

图10 车身垂向振动加速度

图11 悬架动挠度

图12 车轮动载荷

表4表明：在u=30km/h车速下，三个评价指标的均方根值均有增长，其中车身加速度和轮胎动载荷影响较大，悬架动挠度影响较小。说明电机在垂直方向的激振力对车辆的平顺性和操纵稳定性影响较大。双输入下车身加速度均方根值明显加大，严重影响乘坐的舒适性，车轮动载荷的影响比车身加速度更为明显，轮胎与地面的接地性变差，行驶安全性降低，由此引起的车辆操稳性恶化的问题更值得关注[7]。

4 总结

轮毂电机驱动电动汽车因轮毂电机的引入而使非簧载质量增加和电机运行时转矩波动引起的激振力，经过统计车身垂向加速度、悬架动挠度、车轮动载荷三个评价指标的均方根值，可以初步得出：当电动轮汽车以 u=30km/h车速通过B级路面时，非簧载质量增加和垂向激振力均造成了车身垂向加速度均方根值、车轮动载荷均方根值、悬架动挠度的增加，其中，车身垂向加速度和车轮动载荷的波动更加显著。这两个评价指标的显著波动将使平顺性和操控稳定性变差。