FSAE方程式赛车制动系统设计

贺焕利，李亮

（湖北汽车工业学院 汽车动力传动与电子控制湖北省重点实验室，湖北 十堰 442002）

引言

由美国车辆工程师学会于1979年开办的FSAE（Formula SAE）国际学生方程式赛车，在国际上被视为是“学界的F1方程式赛车”[1]。近几年，FSAE赛场上车队无论是数量还是质量都在快速提升，随着竞争日趋激烈，比赛规则日趋完善，同时对FSAE赛车的性能要求也日趋严格。制动系统作为赛车的安全装置，重要性不言而喻，对制动系统的设计要求不仅要满足赛事规则，在紧张激烈的比赛中，保证赛车制动系统的结构可靠、性能稳定，而且应符合人机工程及轻量化的要求，这无疑对制赛车动系统的设计者提出更高的要求。本文依托湖北汽车工业学院东风 HUAT车队HUAT E12方程赛车研发项目，设计开发了一款结构安全可靠、性能稳定且符合人机工程的赛车制动系统。

1 赛车制动系统设计方案

《中国大学生方程式汽车大赛规则》中对制动性能有明确规定，考虑到FSAE方程式赛车对轻量化、人机工程等方面的设计要求，选择了立式主缸布置形式。立式主缸的主要优势在于可以设计更大的踏板传力比，将车手施加在踏板上的力进行放大。目前，方程式赛车中常见的立式主缸品牌有三个，即 tilton、AP Racing和卡瑞森，出于经济性考虑，本次设计选用卡瑞森的立式主缸。

制动盘的安装选用浮动连接，赛车制动盘在制动时，一般负载较大，制动时产生大量热能，当制动盘受力不均时，容易导致制动盘产生形变、动力不稳定，降低赛车的操控性能。选用浮动盘的结构，则可以通过轴向和径向的轻微移动，在一定程度上缓解制动盘的变形，保证制动稳定性，也能使制动盘两侧的摩擦片磨损更均匀。

管路的布置，采用H型双回路布置。这种布置方便调节前后轮的制动力，既可以达到规则要求的四轮同时抱死，配合左右管路等长的布置，也能保证制动不跑偏，还能根据赛道的情况，在一定范围内对制动分配比进行调节，提升赛车的操控性。

赛车的前卡钳选择后置。当载荷向前转移时，前轮载荷较大，产生大量热能，选用后置有利于散热，在制动开始瞬间，车轮受到的向上的力也能和前轮突然增加的载荷部分抵消，降低车轮附着力突变对制动的影响。后轴卡钳选择前置，制动时载荷前移，导致后轮载荷小，热量相对较少，散热要求相对较低，也能有效保证后轮制动温度不会过低。在制动开始瞬间，车轮受到的向下的力也能和后轮突然减少的载荷部分抵消，使后轮制动力更线性，提升车辆的性能。而且前卡钳后置、后卡钳前置，都更接近质心位置，有利于赛车前后轴荷的分配。

2 制动系统关键部件设计

2.1 制动过程受力分析

赛车制动时，赛车受力图如图1所示：

图1 赛车受力简图

根据汽车理论知识，分别对赛车的前、后轮接地点取矩，可以得到：

式中，FN1：地面对前轮的法向反作用力；FN2：地面对后轮的法向反作用力；G：赛车的重力；L：赛车轴距；a：赛车质心至前轴轴线的距离；b：赛车质心至后轴轴线的距离；hg：赛车质心高度；φ：附着系数。制动时，车轮受力如图2所示，Fb：地面制动力；Tu：车轮制动器的摩擦片与制动盘相对滑转时的摩擦力矩；Fu：制动器制动力；r：车轮滚动半径。

图2 车轮的受力简图

在车轮周缘产生的、用于克服制动器摩擦力矩所需要的力称为制动器制动力，用Fu表示。

最大地面制动力：

前、后轴制动力分配关系如下：

式中，β：制动力分配系数；Fu1：前轴的制动器的制动力；Fu2：后轴制动器的制动力。在车轮抱死前，车轮对轴的力矩和摩擦片与制动盘产生的摩擦力矩是平衡的，由此可得：

式中，r1：制动盘的有效摩擦半径，一般为轮辋的70%-79%；μ：摩擦片与制动之间的摩擦系数；F钳：卡钳对制动盘的夹紧力，摩擦片与制动盘之间的摩擦系数一般在0.35～0.45。卡钳对制动盘的夹紧力为：

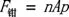
式中，A：卡钳的活塞面积；n：卡钳的活塞数量。

2.2 匹配分析

2.2.1 主缸尺寸计算

主缸工作容积为：

式中，d0：制动主缸的直径；δ0：主缸活塞在完全制动时的行程，一般取δ0=（0.8～1.2）d0。

2.2.2 卡钳尺寸计算

制动卡钳的工作容积为：

式中，δ：卡钳活塞完全制动时的行程；d：卡钳活塞的直径。制动时，制动管路在压力作用下会有一定的膨胀，不同管路膨胀系数不同，方程式赛车使用的管路，一般取1.1，封闭管路中，压力处处相等。因此，以前轴为例，可以得到主缸与卡钳的容积为：

管路压力为：

式中，F：完全制动时制动踏板力，一般取值不超过500N，取值过大，会使制动踏板沉重，取值过小，容易出现车轮抱死，不利于车手驾驶；A1：与前轴卡钳相连的主缸的活塞面积；k1：制动踏板的杠杆比；k2：平衡杆将踏板力分给前主缸的百分比。

联立式（3）、（4）、（5）、（6），则可得：

式中，F、δ0、n、δ和P确定后，通过上式计算出卡钳活塞直径d，进而计算出与前卡钳相连主缸活塞的尺寸。同理，可计算出后轴的卡钳和主缸的尺寸。

2.3 制动距离的计算

赛车在硬质沥青路面上制动时有三种情况：

1）当φ＜φ0时，最大减速度为：

2）当φ＞φ0时，最大减速度为：

3）当φ=φ0时，最大减速度为：

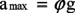
式中，φ0：同步附着系数；φ：附着系数。

图3 制动过程

赛车制动距离可由下式计算：

其中，τ2'：制动响应时间；τ2''：制动减速度上升时间；τ4：制动释放时间；v：制动初速度。如图3所示，b点以前称之为车手反应时间，一般为0.3～1.0s，b到c为制动响应时间，由于赛车的制动设计的较为灵敏，这里取0.1s，c点到e点称之为制动力增长阶段，由于赛车的制动行程设计较短，灵敏度高，所以取 0.2s，则τ2'+τ2''/2=0.2s；f到g一般为0.2～1.0s，本文取 0.2s。

2.4 制动效率计算

前、后轴的利用附着系数分

式中，Fxb1：赛车前轴的地面制动力；Fxb2：赛车后轴的地面制动力；z：制动强度。由式（9）和（10）可得前、后轴制动效率分别为：

式中，Ef：赛车前轴制动效率；Er：赛车后轴制动效率。

3 制动系统优化设计

3.1 系统优化约束条件

在赛车制动的过程中，如果后轮比前轮先抱死，容易发生后轴侧滑，导致赛车失去控制。为了尽量避免赛车出现危险工况，取φr≤φ≤φf。将式（11）和（12）代入其中，可得制动力分配比的极限关系为：

式中，z：整车应达到的最小制动强度。由于方程式赛车使用的是热熔胎，最大附着系数可以达到1.4，根据式（13）可以初步确定在0.2（湿滑路面）≤φ≤1.4（干燥路面）的条件下，制动力分配比允许范围的表达式。

确定目标函数和约束条件：当附着系数φ在0.2～1.4时，应该尽可能的靠近临界附着系数，因为这时地面和车轮的附着能力利用最为充分，制动分配系数也达到最佳值。由于赛车本身的质量很轻，且赛车只乘坐车手一人，车手的体重也相差较小，因此在任何项目中，赛车质量和重心位置变化都非常小，可以视赛车的质量G和质心高度hg都是恒定不变的。所以，在这里只对赛车满载工况进行分析。根据赛车满载时前、后轴实际利用附着系数，使实际值与理想值差值的平方和最小，建立目标函数为：

由式（9）和（10）得到φf、φr与β的关系，代入式（14）得目标函数为：

对于制动强度，联合国欧洲经济委员会汽车法规（ECE）中有要求。但是，该法规适用于民用汽车，是通用标准。本文中所研究的大学生方程式赛车，在结构、质量、使用的轮胎的附着系数、驾驶路况和使用工况都与民用车有所不同。这里的计算，参考ECE法规的规定，做适当调整。由于所设计的方程式赛车为单人驾驶，与M1类车辆更为接近，所以参考M1类车辆的标准，给出约束条件如下：

1）如果制动强度在 z=0.1～1.12（由 z≥0.1+0.85（φ-0.2）得到）范围内时，曲线φf应该在曲线φr的上方，并且前、后轴利用附着系数都应该满足φf，φr≤(z+0.07)/0.85。

2）如果制动强度在z=0.3～0.45范围内时，曲线φf应该在曲线φr的上方；如果曲线φr没有超过直线φ＝z+0.05的条件下，曲线φr可以在曲线φf的上方。但是考虑到赛车在赛道上的速度较高，出于安全考虑，在设计中不允许后轮比前轮先抱死。 因此，数学约束条件为：

将φf和φr换为与设计变量β有关的函数，得：

式中，hg：赛车质心高度； L：赛车的轴距（即前轴轴线至后轴轴线的水平距离）。

3.2 仿真模型

整车主要参数见表1。

表1 HUAT E12号赛车参数

图4 函数关系图

参数优化完成后，会得到F(β)min的结果（如图4所示），图中方差最小处，对应的横坐标是该函数求最优解时的初始值为0.65，将该初始值代入目标函数，即可求出在约束条件下的最优制动力分配系数β=0.632，赛车的同步附着系数φ0=0.826。

系统仿真模型如图5所示。

图5 系统仿真模型

4 仿真结果分析

仿真结果显示β线和满载I曲线相交于A点，如图6所示，此时的附着系数（即同步附着系数）φ0=0.826，其所对应的制动减速度称为临界减速度。

图6 HUAT E12号赛车的β线和I曲线

当z=0.826时，前、后轴利用附着系数均为0.826，图7所示。即无任何车轮抱死所要求的地面附着系数为0.826。

图7 利用附着系数与制动强度的关系

HUAT E12号赛车在制动力分配系数β=0.632时，制动效率与附着系数的关系（如图8所示），前轴的制动效率在φ=0.826之前，呈上升趋势，φ=0.826时，前、后轴的制动效率都为100%，此时，四轮都达到附着极限，即将抱死。φ＞0.826时，后轴附着系数从100%开始降低，当利用附着系数达到1.3时，后轴制动效率为75%，此时，制动减速度不是1.3g，而只有1.3×75%=0.975g，为最大减速度。利用附着系数达到最大值时，Er=68%。

图8 制动效率与附着系数关系图

HUAT E12号赛车在初速度为100km/h时，制动距离与利用附着系数之间的关系，如图9所示，当利用附着系数小于0.48时，制动距离超过100m，当其从0.48开始逐渐增大时，制动距离逐渐缩短，而且缩短的趋势由快到慢，当利用附着系数达到最大值1.4时，制动距离仅有29.7m。因此，当赛车在直线加速尾端减速制动到30km/h左右时，制动距离将小于30m，制动距离在赛道尾端的减速区域内。因此，满足使用要求。

图9 制动距离与利用附着系数的关系(100km/h)

HUAT E12号赛车在初速度为70km/h时，制动距离与利用附着系数之间的关系（如图10所示），利用附着系数小于0.24时，制动距离在100m以上，大于0.24时，制动距离随着附着系数的增长快速缩减，利用附着系数达到1.0左右时，缩减速度趋于平缓，当利用附着系数达到最大值1.4时，制动距离缩减到了16.3m。

FSAE方程式赛车在高速避障和耐久测试这两个项目中，赛车的平均速度一般在70km/h左右，从分析结果来看，干燥的赛道环境下制动距离在16.3～21.8m。赛车在高速避障和耐久测试中，从小直道加速后，从70km/h减速到30km/h时，制动距离小于10m，制动效果满足车手使用需求。

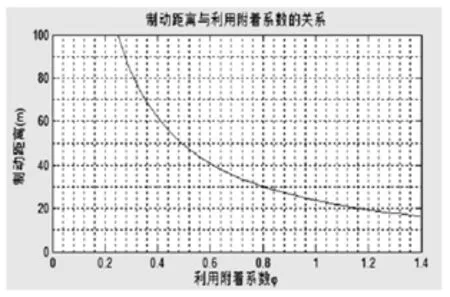
图10 制动距离与利用附着系数的关系(70km/h)

5 结论

通过本次研究：得到制动力分配系数β=0.632，同步附着系数φ0=0.826；设计参数为：制动主缸（缸径16mm）、制动卡钳（缸径32mm和28mm），制动盘（四个铆钉连接的浮动盘、直径分别为192mm和182mm）；仿真结果显示路面干燥的情况下，初速度100km/h时，制动距离为30.83m。赛车上安装了制动平衡杆（制动力分配装置），能实现赛车的制动力分配系数可调，达到四轮同时抱死的要求。经过实车验证，本设计方案满足大赛要求，研究成果对FSAE赛车的设计、制造及调校有一定的指导意义。