我国银行业系统性风险度量

吴秋实 陈琪

关键词：CoVaR方法;系统性风险;上市银行;度量

中图分类号：F83 文献标识码：A

收录日期：2018年12月20日

引言

2007年8月的次贷危机，席卷了美国、欧盟、日本等世界主要金融市场，使国际金融市场产生了强烈的信贷紧缩效应，对国际金融秩序造成了极大的冲击，国际金融体系长期积累的系统性金融风险得以暴露，并引发了2008年席卷全球的金融危机，对全球金融市场产生了巨大的破坏力。面对金融经济的全球化，单个金融机构、单个金融市场或者单个国家发生金融风险往往会迅速扩散到其他金融机构、金融市场乃至国家，即整个金融体系，从而引发危害全球的系统性风险。面对治理系统性风险的迫切性，研究系统性风险的度量就显得尤为重要。巴塞尔银行监管委员会提出的《巴塞尔协议Ⅲ》新增了系统性风险的内容，监管要求的提出将增加对系统性银行的后备资本要求。本文通过分位数回归的CoVaR模型对我国银行业系统性风险进行度量，在一定程度上能够对控制我国银行业系统性风险提供参考意见。

一、相关定义及度量方法

（一）银行系统性风险的定义

1、国外研究。美国芝加哥大学经济学教授Kaufaman认为，系统性风险是一个事件在一连串机构和市场构成的系统中引起一系列连续损失的可能性，银行业系统性风险是指由第一部分银行业系统性风险特征及危害于银行系统的一个参与者不能履约，从而引起其他参与者违约，进而引发的链式反应而导致的广泛的金融困难的可能性;IMF的官员Hermosillo认为，银行业系统性风险是使得其他不相干的经济体遭受经济损失的某种外部性，这种外部性表现为传染性与风险溢出性;国际清算银行定义系统性风险为金融体系内部一些或者全部机构出现损失后导致金融服务被破坏的可能性，而且该风险可能会对实体经济产生严重的负面影响;欧洲中央银行对系统性风险的定义则为：普遍存在的、损害金融体系功能的风险。

2、国内研究。包全永认为广义的银行业系统性风险是指银行体系资金融通等基本功能丧失的可能性，狭义的银行业系统性风险是指主要银行失败的负外部性造成其他银行经营受到影响，进而导致银行体系丧失基本功能的可能性;翟金林在讨论银行业系统性风险时引进了银行系统性事件和银行系性危机两个概念。银行系统性事件是指与一家银行遭遇困难甚至是银行失败或崩溃或一个金融市场崩溃相关的坏消息而引起的一连串的银行机构或金融市场严重的逆效应，如一连串的银行倒闭或崩溃。银行系统性危机是指一个系统性事件对银行体系大规模的冲击影响了相当数量的银行，并导致大量金融机构或金融市场的逆效应，从而严重削弱了银行体系乃至金融体系的基本的健康机能，而这种机能是金融体系保持稳定与高回报的基础。北京大学经济社会与文化研究中心的米运生认为，银行业系统性风险分为静态条件下的系统性风险和动态条件下的系统性风险。静态条件下的系统性银行风险也称为市场风险，它是整个银行系统所遭遇的风险，并且与市场的货币、通货膨胀率波动利率等相联系的风险。动态条件下的系统性银行风险在现实的经济生活中，即使在一个竞争充分的间接融资市场上，系统性银行风险也并不会因为没有垄断银行的存在而得以避免。

（二）银行系统性风险度量方法。Lehar应用Merton的模型，研究在资产收益正态分布原假设下，给出金融机构联合违约概率来度量系统性金融风险，并且通过预期损失分别计算一个银行对于银行系统整体风险的贡献程度并进行比较。宋群英应用阿基米德Coupla函数来分析中国的银行系统间的风险传染性。高国华、潘英丽构建了GARCH-CoVaR模型，进而研究我国上市商业银行的系统性风险贡献度及其影响因素。丁庭栋、赵晓慧运用分位数回归的CoVa方法，研究我国国内多元金融服务业、银行業、保险业及房地产行业之间以及对金融系统整体的波动溢出效应。陈守东、王妍选取了证券市场、外汇市场、银行部门的相关指标，构建了一个金融压力指数来研究中国金融系统的压力。CoVaR法是Adrian和Brunnermeier于2008年基于风险价值（VaR）提出的衡量系统性风险的方法。根据CoVaR计算方法的不同，现有的研究主要分为两类：分位数回归法和GARCH模型法。分位数回归法的优点在于不需要对于分布做出特定的假设，也不局限于特定的模型，能够很好地解决极值问题，确保回归模型的稳健性和有效性;缺点在于其一般刻画的是线性结构，对于非线性结构的刻画存在一定缺陷。国内学者主要研究如下：谢福座（2010）运用分位数回归法研究了我国债券市场和股票市场之间的金融溢出效应。陈守东、王妍（2014）引进极值理论，度量了我国上市金融机构对整体金融系统的风险贡献，并且给出了我国系统重要性金融机构名单。冉茂盛、唐潇（2015）加入时变性，运用分位数回归法研究我国银行、保险和证券业上市金融机构对金融系统的风险贡献。GARCH模型法的优点在于对于误差的方差进行了进一步假设，且可以根据实际数据要求适用不同的形式;缺点在于对于误差分布的假设如果不当会影响结果的准确度，且整体回归模型缺乏一定的稳健性。主要研究如下：高国华、潘英丽（2011）基于动态CoVaR方法计算了我国上市银行对金融系统的风险贡献及其影响因素。沈悦等（2014）基于CARCH-Copula-CoVaR模型研究了我国银行、保险、证券和信托这四个子行业对于金融体系的风险贡献，以及这四个子行业相互之间的风险溢出。由于分位数回归方法使用更为普遍且其稳健性更高，所以本文采用分位数回归方法来构建系统性风险计量的CoVaR模型。

本文的创新点与不足之处：本文采用分位数回归的CoVaR模型来度量我国银行业的系统性风险，引用分位数回归方法的稳健性和有效性更高，能够很好地解决极值问题，但是它的不足之处是不能很好地刻画非线性结构。本文研究的创新之处在于：（1）采用非平衡面板数据，引用了2006年10月至2018年10月的股票日收盘价格数据，采用的都是最新的数据，且具有代表性;（2）本研究包含了我国2018年中美贸易战时期的数据，因此研究结果对于应对今后可能发生的金融危机具有指导意义;（3）本文选取的是16家上市银行的数据，相比以前的14家上市银行的数据更加全面、更加可靠。

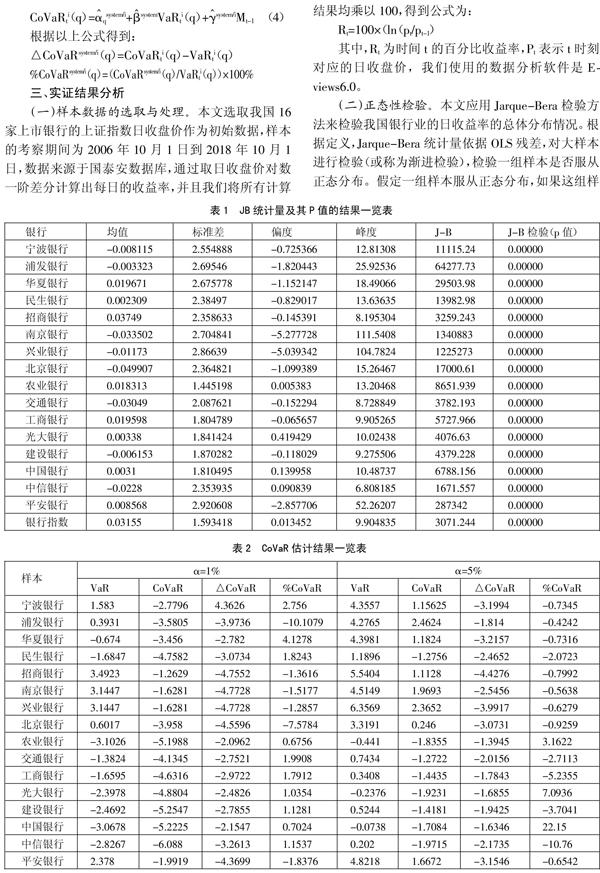
本服从正态分布，如果这组样本JB统计量的相伴概率值小于设定值，则拒绝服从正态分布的原假设;如果JB统计量的相伴概率值小于设定值，则接受服从正态分布的原假设。因此，笔者通过用数据分析软件Eviews6.0对2006年10月1日至2018年10月1日期间各个银行股票价格的日收盘收益率和银行系统指数的日收益率进行JB检验，其JB统计量及其P值的结果如表1所示。从表1中可以明显得出结论：首先，可以看出在所研究的银行中，它们的日收益率的均值和标准差都相差不大，所以相对来说他们的变动是非常稳定的;其次，我们可以看出所有银行J-B检验的p值都是接近于0的，因此在99%的置信水平上我们可以拒绝“单个银行的股票价格日收益率序列服从正态分布这一假设”，也就是说，16家商业银行的股票价格日收益率和银行系统的指数收益率均不服从正态分布。（表1）

（三）CoVaR结果分析。本文在置信水平q=1%、5%的置信水平下进行计算，其中可以通过求收益率系列分布的q得到，而CoVaRqj/i则表示当Xi=VaRi条件下的Xj的风险价值，根据前述公式，可以得到的相应结果如表2所示。（表2）

从表2中我们可以看出：（1）从Var的结果来看，在不同的分位点下不同银行的Var值有所差异，并且有正有负。在1%的置信水平下，中国银行、建设银行、农业银行、中信银行的日平均Var损失值较大，在5%的置信水平下，农业银行、光大银行、中国银行的Var为负数，因此其潜在的风险损失较大;（2）从CoVar的结果来看，在1%和5%的置信水平下，CoVar的结果都是小于0的，且中信银行、中国银行、建设银行、农业银行的CoVar的影响是极其显著的。CoVar能够度量单个银行对整个银行业体系的影响和贡献，说明中信银行、中国银行、建设银行、农业银行这几个大型的银行机构对银行体系的影响和贡献比其他银行机构的影响和贡献显著;（3）从△CoVaR和%CoVaR的结果来看，在1%和5%的置信水平下，各个银行的△CoVaR和%CoVaR值都各不相同，△CoVaR和%CoVaR可以表示为当单个银行机构陷入危机时，对整个银行体系的风险溢出影响。综合1%和5%的置信水平下的△CoVaR和%CoVaR的结果可以看出，中信银行、中国银行、工商银行、农业银行、建设银行等银行都伴随着较大的风险溢出效应，其中，中国银行最为明显。说明对银行业而言，规模较大的全国性商业银行表现为系统性重要银行，它们面临极端风险时对银行业的溢出效应会更加明显。

四、结论

本文引用Tobias Adrian和Markus K.Brunnermeier提出的CoVaR模型，选取国泰安数据库的股票日收盘价格数据，并运用分位数回归的CoVaR模型对我国的16家上市银行的系统性风险贡献度进行度量，捕捉到当单个银行机构发生极端事件时对整个银行系统的风险溢出效应。通过比较我国16家上市银行的研究数据，我们发现，我国比较大型的全国性的商业银行的风险溢出效应比较大，例如中信银行、中国银行、工商银行、农业银行、建设银行等大型银行，其对我国银行业系统性风险的影响和作用是非常显著，其中一个大型银行发生风险变动对我国的整个银行体系的影响将会是巨大的。因此，在我国现有的监管体制下，相关金融监管机构应该加大对银行业的监管力度，特别是像我国四大国有银行这样系统性比较重要的银行，应该对其资产结构、信贷结构、存貸比率、不良贷款率等实施更加严厉的监管，因为只有这样，才能确保我国的金融体系的稳健性，防止金融危机的发生，抑制金融风险的扩散。

主要参考文献：

[1]Lehar A.Measuring systemic risk：A risk management approach[J].Journal of Banking and Finance，2005.29（10）.

[2]Guidance to assess the systemic importance of financial institutions Markets and instruments：Initial considerations[R].Background Paper（Basel），2009.

[3]Kaufman G.G..Bank Failures，Systemic Risk，and Bank Regulation[J].Cato J，1996（16）.

[4]Bank for International Settlements.Guidance to Assess the Systemic Importance of Financial Institutions，Markets and Instruments：Initial Considerations [R].Report to G20 Finance Ministers and Governors，Financial Stability Board，2009.

[5]European Central Bank.Financial Networks and Financial Stability [J].Financial Stability Review，2010（6）.

[6]Tobias T.Brunnermeier M K.CoVaR[J].Working ，2011.

[7]包全永.银行系统性风险的传染模型研究[J].金融研究，2005（8）.

[8]宋群英.基于Copula函数的系统重要性银行的传染性研究[J].金融与经济，2011（10）.

[9]翟金林.银行系统性风险研究[D].南开大学，2001.

[10]丁庭栋，赵晓慧.不同行业与金融系统的波动溢出效应分析[J].统计与决策，2012（3）.