狭义相对论体系下惯性系与非惯性系的不对等性问题探讨
杨习志
(昆明市第一中学 云南 昆明 650031)
赵 坚
(昆明市五华区基础教育科学研究中心 云南 昆明 650031)
孙 彪
(昆明市第一中学 云南 昆明 650031)
1 问题提出
在狭义相对论章节的教学中,总会遇到学生问一些涉及加速运动的争议性问题,这些争议性问题的关键就在于是否搞清楚狭义相对论体系下惯性系与非惯性系、惯性运动与非惯性运动之间是否对等的问题,比如下面两个问题.
问题1:到底谁在辐射电磁波?
众所周知,电子做加速运动时会辐射电磁波,假设有两个电子A与B,B相对于地面静止,A相对于地面做加速运动,假设A会辐射电磁波.现在的问题是,既然运动是相对的,在A看来,是B相对于A做加速运动, B也应该辐射电磁波,那么到底是谁在辐射电磁波?电磁波具有能量,发射电磁波可以看成是一种能量输出或耗散,即发射电磁波是一件确定的事实,按理不应该存在相对性的问题,绝大多数观点当然是只承认A会辐射电磁波,但却无法清楚地说服前面的提问.另外,如果确定是A辐射电磁波,加速运动的相对性在这里便不成立,即一定有一方是特殊的可区分的,那么如何区分便是一个非常重要的问题.
问题2:到底谁更年轻?
双生子效应是一个非常著名的狭义相对论的思想性实验,曾经引起了较大的争议和讨论.即一对孪生子A和B,A呆在地球上,B坐着飞船加速而去,若干年后再返回地球,那么到底谁更年轻?结论当然是坐着飞船离开再回来的B更年轻,即做变速运动的一方更年轻.问题在于,既然运动是相对的,那么在B看来是A在做加速运动,应该是A更年轻才对?这是关于双生子效应中被问及最多的问题,也是最不容易争论清楚的问题.可以肯定的是结论是唯一的,因为A与B已经碰面在一起,谁年轻必定是个事实,因此,这个问题的关键就在于到底加速运动有没有相对性?或惯性运动和非惯性运动是否对等?如果不对等,那么这种不对等性体现在哪里?
2 加速运动的研究体系划分
任何问题的讨论都是在一定的范围或体系下进行的,由于加速运动问题的探讨到底属于狭义相对论范畴还是广义相对论范畴存在着很多争议,故在探讨以上问题时,不得不说清楚加速运动的研究体系问题.狭义相对论和广义相对论是两个完全不同的研究体系,区分狭义相对论和广义相对论的根本问题在于时空背景,如果研究问题的时空背景是无引力的或弱引力的平直时空,又称闵可夫斯基时空,则属于狭义相对论研究体系,如果研究问题的时空背景是有引力的或强引力的弯曲时空,又称黎曼时空,则属于广义相对论研究体系.以上所讨论问题的时空背景均属于平直时空问题,故均属于狭义相对论研究体系,应在狭义相对论的大前提下进行讨论.值得注意的是到现在依然有很多人认为双生子佯谬问题涉及加速运动,应属于广义相对论研究范畴,理由是根据等效原理,即加速场与引力场等效,因此加速运动会产生引力效应,造成时空弯曲,故属于广义相对论研究范畴.这是一种极其错误的理解,等效原理只是一种局域等效,因为加速场是平行的,而引力场是汇聚的,二者不可能完全等效,故引力也有真引力与假引力之分,真引力的时空曲率不为零,而假引力的时空曲率是为零的,它是由于观者做非惯性运动而产生的一种表观引力,因此以上提到的加速运动问题仍属于狭义相对论研究范畴.
3 闵式时空与双生子效应结论的绝对性在惯性运动与非惯性运动不平权下的具体体现
随着闵可夫斯基时空图的出现,对惯性系或惯性运动的定义显得方便了一些,如图1所示,闵可夫斯基时空将时间与空间连成一个整体,构成时空图,物体所发生的事件在时空图中所画出的线称为世界线.为方便讨论,空间维度只考虑一维,以双生子效应为例,静止于地球上的观察者和地球(不考虑地球的自转)都将画出图中甲所示的世界线.坐飞船变速离去又变速回来的观察者将画出图中乙所示的世界线.世界线上的每一小段微元叫做线元(间隔),其长度可表示为[1]
ds2=-c2dt2+dx2+dy2+dz2
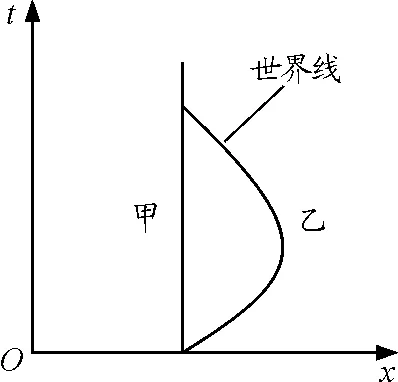
图1 闵可夫斯基时空图
若为二维时空,则有ds2=-c2dt2+dx2,这与欧氏空间中两点之间距离的计算有点类似,但更重要的特点是线元的长度是洛伦兹协变的,与参考系的选取无关,这里可以给出简单证明,根据洛伦兹变换有
x′=(x-vt)γ
则
ds′2=-c2dt′2+dx′2=
-c2dt2+dx2
可见,线元的长度与参考系的选取无关,这对讨论双生子效应结论的唯一性有着非常重要的作用.其次,以甲为例,由于dx=0,则有
ds2=-c2dt2=-c2dτ2
其中dt是坐标时,与坐标系的选取有关,dτ是固有时间,即以自己为参考系而得出的时间,这个时间是与坐标系的选取无关的,可见世界线的长度可代表物体经历的固有时,即
或
注意乙的世界线虽为曲线,若只需定性讨论,可以将其分割成无数的小段,当分割成无限段时,每一小段即变成了直线,故仍可以通过洛伦兹变换变成如甲所示的直线,同样可以得出乙的世界线长度即为乙经历的固有时.又由于线元的长度是与参考系无关的,故可以得出结论,即质点世界线的长度就是质点所经历的固有时,且与参考系的选取无关.这样一来,要比较谁更年轻则只需要比较世界线的长度即可.注意与欧氏空间所不同的是,在闵式时空中直线为最长线,没有最短线,故乙的世界线将更短,乙更年轻,且与参考系的选取无关.
以上用闵式时空图来探讨双生子效应是非常直观和方便的,但也有不少学者认为时空图中无法具体给出乙做变速运动的曲线方程,无法进行定量的计算,故不太愿意承认这种方式的讨论.为增强说服力,笔者将乙的运动简化为折线运动以便进行定量的计算,注意折线运动也是变速运动.即乙坐着飞船匀速离开,再匀速返回,但关键问题在于乙既然做匀速运动就不可能返回,为此,可在某个时刻假设有另一艘飞船向着地球飞来,并在与乙相遇的时刻进行时间校准,以此来等效乙的返回过程,若以地球为参考系,可作出如图2所示的时空图,此时,只需要比较世界线LOA与LOBA的长度即可[4].

图2 以地球为参考系的时空图
即
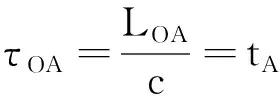
又
x=vt
即
又
故
τOBA=2γ-1tB=γ-1tA=γ-1τOA
τOBA<τOA
即乙更年轻.

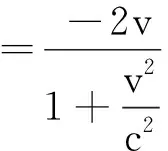
故可得其世界线如图3中B′A′所示.

图3 以乙为参考系的时空图
即
又
LO′B′=γ-1ctC
故
即
又
τO′B′A′=τO′B′+τB′A′=2γ-1tC
故
τO′A′=γ-1τO′B′A′
即
τO′A′>τO′B′A′
故还是乙更年轻.
通过以上计算可以看出,无论是以地球上的观察者甲为参考系,还是以飞船上的观察者乙为参考系,最终的结论都是乙更年轻,即做变速运动的一方更年轻,结论是唯一的,故匀速运动与变速运动之间不存在相对性,它们之间是不对称不平权的.
4 打破惯性系与非惯性系对称性的根源是什么?
狭义相对性原理指出一切物理规律在惯性参照系中均有相同的形式,它反映了惯性参照系都是等价平权的,没有特殊性的,它的定量描述即物理规律的表达形式必须是洛伦兹协变的,即物理规律的表达式必须服从洛伦兹变换.其次,洛伦兹变换本身就是惯性系之间的坐标变换,因此可以肯定的是无论是定性描述还是定量描述,狭义相对论体系下都只承认物理规律在惯性系中具有相同形式,无法区分,即只有惯性系之间是平权的.那么自然可以得知,物理规律在非惯性系中将不再具有相同形式,即惯性系与非惯性系之间不再具有对称性,它们是不平权的,那么打破这一对称性的根源究竟是什么呢?
在狭义相对论中出现惯性系与非惯性系的不对称性是不可避免的,也是无法改变的,其根本原因来自于力的存在,尤其是引力的存在,让爱因斯坦尤为感到困惑,因为引力无论如何也无法纳入狭义相对论体系,它无法服从洛伦兹协变.于是爱因斯坦被迫另辟蹊径创立了广义相对论,将加速运动产生的效果与引力等效,称为等效原理,由于在加速场中的观察者将看到光线走弯曲的路径,因此在引力场中的观察者也应看到光线走弯曲的路径,于是引力造成了时空的弯曲,引力被巧妙地变成了弯曲的时空背景,力消除了,于是对称性又出现了,在广义相对论体系下,一切参考系又都平权了,即物理定律的表达式在任意坐标变换下形式不变,称为广义相对性原理.因此,对于坐着飞船加速离开又加速返回的乙之所以处于特殊状态,就是因为飞船要做变速运动时发动机必须工作为飞船提供推力,正是这个推力的存在打破了甲与乙的对称性.
5 惯性系与非惯性系惯性运动与非惯性运动
虽然狭义相对论要求物理规律在惯性系中具有相同的形式,但其自身却没有对惯性系做过明确定义,究其原因:第一,在狭义相对论时空背景下惯性系与非惯性系、惯性运动与非惯性运动是泾渭分明,绝不模棱两可的,即指定一个物体或一种运动,说它是惯性系或惯性运动是十分清楚的,如前面提到的加速运动的飞船就是非惯性系或做非惯性运动,但由于缺乏定量的可操作性的描述,也因此常常引发争论.再如问题1中提到的电子,根据以上讨论虽然可以肯定的是只有做非惯性运动的电子才会辐射电磁波,但问题是到底谁在真正地做非惯性运动?第二,洛伦兹变换是惯性坐标系之间的变换,这个变换本身就已经给出了惯性系的特点,即惯性坐标系之间是洛伦兹协变的.当然,我们也可以从惯性系所要求的特点给出惯性系的定义,狭义相对论中的惯性系要求其时空必定是均匀的且各向同性的,这等价于不受力的作用,因为力的作用会打破这种对称性,故不受力的物体可以看作惯性系,这与我们通常对惯性系的定义是一致的,即相对于孤立质点(不受力)静止或做匀速直线运动的物体可看作惯性系,反之则为非惯性系;同样,相对于孤立质点(不受力)静止或做匀速直线的运动就称为惯性运动,反之则称为非惯性运动.然而,这样定义的弊端就是我们还得定义孤立质点以及不受力等问题,这势必又会引发新的循环论证.关于此问题的讨论,在梁灿彬教授所著的《微分几何与广义相对论入门》里面有较为详尽的定量解释,这里仅给出结论[1],即当且仅当质点的世界线是类时测地线时,质点的运动称为惯性运动;反之则为非惯性运动.其次,加速度又有三维加速度与四维加速度之分,三维加速度与参考系的选取有关,而四维加速度是绝对的与参考系无关的.当质点做惯性运动时,其四维加速度必定为零,当质点做非惯性运动时,其四维加速度必定不为零.当把加速运动理解为非惯性运动时,其加速运动必然是一种四维加速度不为零的、绝对的,与参考系无关的运动.

