零吸引符号子带自适应滤波算法*
郭 莹,关思秀
(沈阳工业大学 信息科学与工程学院,辽宁 沈阳 110870)
0 引 言
自适应滤波算法在各领域有着广泛应用,如回声消除、系统辨识、自适应信道均衡和信号预测 等[1-3]。传统的LMS算法操作简单易实现[4],RLS算法收敛速度快,但其计算复杂度较高[5]。若输入信号是强相关性的有色信号或语音信号,这两种算法的收敛速度将明显变慢。子带自适应滤波技术能够有效解决此问题[6]。子带自适应滤波器通过滤波器组分割输入信号从而降低输入信号的相关性,在各个子带中独立进行算法,可以加快自适应滤波器的收敛速度[7]。在传统的子带自适应滤波器结构中,滤波器的输出端存在混叠分量,使其具有较高的稳态误差。为了解决传统子带自适应滤波器中存在的混叠分量问题,Lee和Gan提出了归一化子带自适应滤波器结构,如图1所示,并推导出归一化子带自适应滤波算法的更新方程[8]。目前,大多数算法都将背景噪声假设为高斯噪声,而现实生活中却广泛存在非高斯冲击噪声,如雷电、报警器、电动机等。基于l2范数的子带自适应滤波算法的性能被这些冲击噪声破坏[9],如归一化子带自适应滤波算法和比例归一化子带自适应滤波算法[10]。考虑到符号类自适应算法可以降低算法复杂度和对冲击噪声有较强的稳健性,文献[11]提出了符号子带自适应滤波(Sign Subband Adaptive Filter,SSAF)。需要说明的是,以上算法均并未考虑系统的稀疏特性[12](大部分系数为零)。
本文将零吸引因子加入符号子带自适应滤波算法,使其在稀疏系统、背景噪声为非高斯冲击噪声下,具有较快的收敛速度和较低的稳态误差。最后,仿真证明了该算法的有效性。
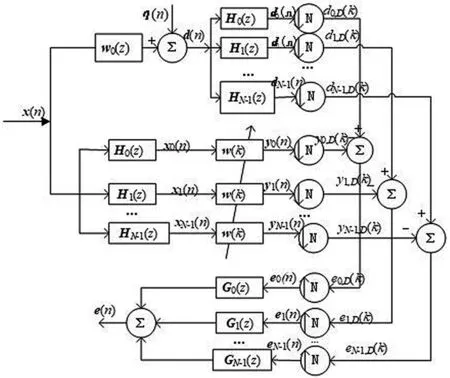
图1 子带自适应滤波器结构
1 传统算法分析
1.1 归一化子带自适应滤波算法
最小扰动原理指的是,自适应滤波器更新后输出要满足一定的约束,一次到下一次迭代,自适应滤波器的系数应当以最小方式变化。Lee和Gan基于最小扰动原理,推导了归一化子带自适应滤波器的更新方程[12]。归一化子带自适应滤波器的结构如图1所示。结构中,Hi(n)和Gi(n)分别为分析滤波器和综合滤波器,其中i=0,1,…,N-1,这里N为常数。x(n)和d(n)经Hi(n)分割后分别产生各自的子带信号xi(n)和di(n),然后将di(n)和yi(n)进行N倍抽取得到di,D(k)和yi,D(k)。这里,n表示抽取前时刻,k表示经过抽取后时刻。于是,第i个子带输出为:

这里,w(k)为自适应滤波器在n=kN时刻的权系数向量,长度为L,且:

由图1可以看出,每个子带中拥有独立的自适应回路,利用误差信号ei,D(k)更新子带自适应滤波器的加权误差,最终最小化误差信号ei,D(k)。第i个子带误差信号为:

受约束的最优化模型见式(4),基于最小扰动原理推导NSAF算法为:

利用拉格朗日乘子法,式(4)可写成如下的代价函数:

其中,λi是拉格朗日乘子。为了求得式(2)的最优值,令可得:
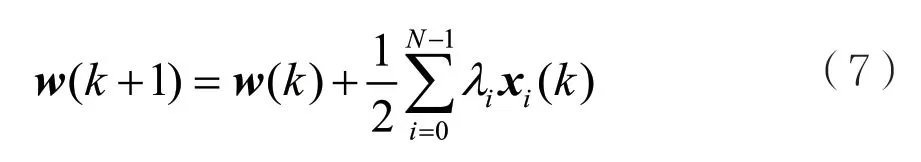
将式(7)代入di,D(k)=wT(k+1)xi(k),得:

其 中,λ=[λ0,λ1,…,λN-1]T是 拉 格 朗 日 乘 子 向量,X(k)=[x0(k),x1(k),…,xN-1(k)]是输入信号矩阵,eD(k)=[e0,D(k),e1,D(k),…,eN-1,D(k)]T是误差向量。式(7)的矩阵形式为:
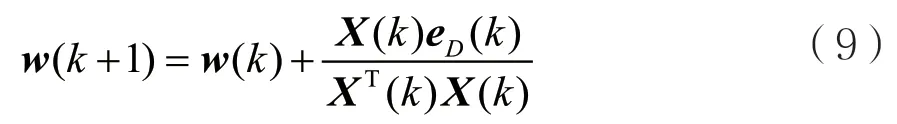
根据余弦调制滤波器组的正交性,有:
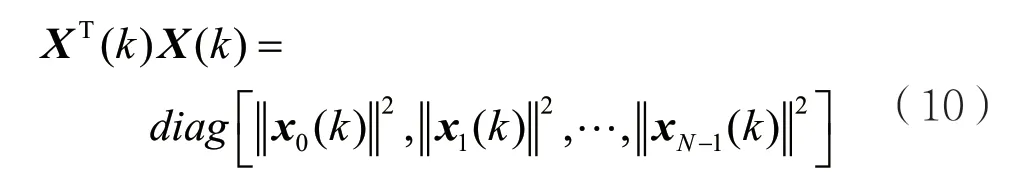
其中diag(·)表示对角矩阵。
得到归一化子带自适应滤波算法的更新公式为:
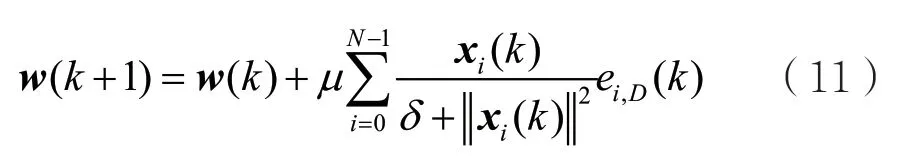
其中,μ为步长参数;δ为正则化参数,用来解决数值计算这一难题。
1.2 符号子带自适应滤波算法
该算法的推导是基于最小扰动原理的受约束最优化问题,结构与图1相同。符号子带自适应滤波算法对脉冲干扰具有较强的鲁棒性。
这里可得第i个子带输出为:

w(k)为自适应滤波器在n=kN时刻的权系数向量,其长度为L,且有:

定义第i个子带误差信号和第i个子带后验误差信号分别为:
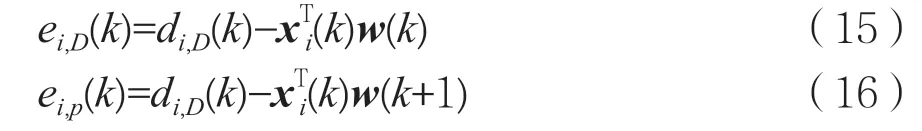
则子带误差向量和子带后验误差向量可分别记为:

其中:

符号子带自适应滤波算法的受约束最优化问题为:
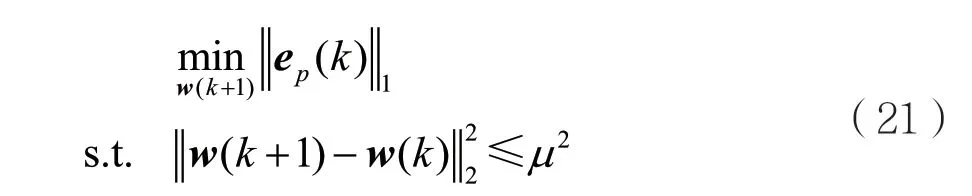
其中,μ为正的步长参数。
代价函数为:

其中,λ为拉格朗日乘子。对式(17)求w(k+1)的导数,得:

其中,sgn(·)表示符号运算,且有:
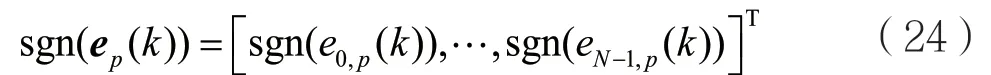

将式(25)带入式(21),得:

使用对角化,假设:

式(26)可简化为:

将式(28)带入式(25),得:
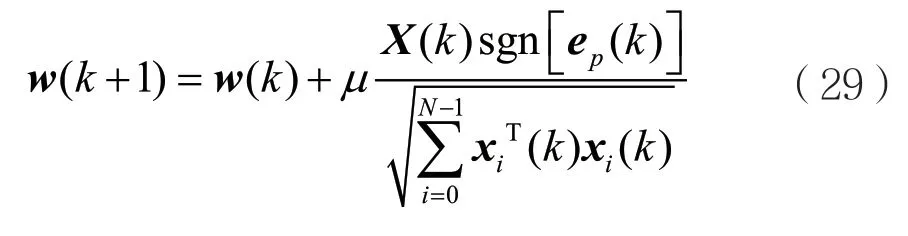
由于后验误差向量在k时刻无法求得,因此用子带误差向量替代,得到权系数更新方程为:
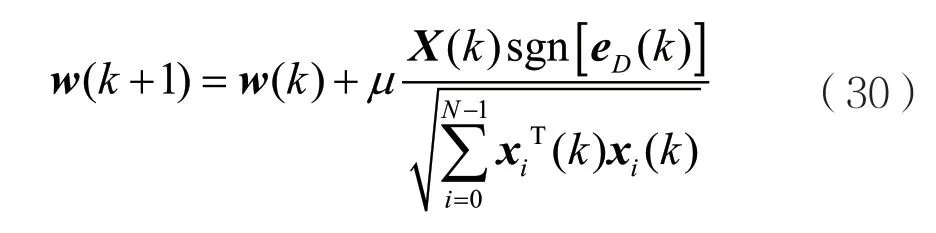
为了克服数值计算困难,将正则化参数δ引入式(30),得:

2 新算法的提出
稀疏信道广泛存在于日常生活,如水下通信信道、通信系统回声信道和无线通信中多径信道等。所谓稀疏特性指的是这些信号和系统中大部分元素取值为零或接近于零,仅有少数元素是非零[13]。结合零吸引因子,使稀疏系统中多数较小元素加快收敛,即零吸引符号子带自适应滤波算法(Zero Attractor Sign Subband Adaptive Filter,ZASSAF)。该算法可以在稀疏系统中抵御非高斯噪声的影响,后文将分析和仿真证明其有效性。
本文将零吸引因子引入SSAF算法。所谓零吸引因子,可以理解为在每次迭代时“吸引”滤波器权系数向零矢量靠近,得到的ZASSAF算法的更新公式:

为提高对稀疏系统的辨识性能,在SSAF算法迭代过程基础上向权系数不断添加一个指向零矢量的修正量,使得在稀疏系统中占主要地位的零系数加速收敛。其中,sgn(·)是一个符号函数。假设符号函数中的变权系数n>0,将会减去一个小的正值υ;当某项权系数n<0,该系数将会增加一个小的正值υ。当未知系统稀疏时,零系数或者较小系数占主要地位,它们的快速收敛将提高整个系统的收敛性能。υ的选取将直接影响算法的收敛性能。具体地,υ太小,向零矢量靠近慢;υ太大,υsgn[w(k)]项带来负面影响,增大了稳态误差。因此,选择合适的υ值对算法具有重要意义[14]。在稀疏系统辨识问题中,ZASSAF比SSSAF具有更好的收敛性能。
3 实验结果
3.1 实验条件
3.2 性能指标及参数设置
仿真实验在等效步长条件下进行,选取均方偏差(Mean Square Deviation,MSD)收敛曲线作为评价实验结果的好坏。所有均方偏差曲线为20次独立实验取平均的结果,单位为分贝(dB)。

3.3 仿真结果及分析
本文实验是在公平原则下进行的。将各算法应用的到系统辨识系统中并进行MATLAB仿真实验,且为了避免偶然性,每个仿真都是30次独立实验的平均结果。
3.3.1 NLMS算法与NSAF算法性能比较
高斯噪声条件下,非稀疏信道信道为图2(b),输入信号由零均值高斯白噪声通过一阶AR系统产生。比较分析NLMS算法与NSAF算法的性能,仿真结果如图3所示。

图2 仿真中用的信道

表2 参数设置
当输入信号为有色信号时,NLMS算法与NSAF子带数为2、4、8时进行对比。可以看出,NLMS算法收敛速度变慢,NSAF算法具有更快的收敛速度。此外,随着子带数目的增加,收敛速度相对变快,但是随着子带数目的增多,计算复杂度增高。实验仿真子带数为4。

图3 NLMS算法与NSAF算法在高斯噪声条件下性能比较
3.3.2 输入信号为有色信号,各算法在稀疏信道、高斯噪声条件下的性能比较
稀疏信道信道为图2(a)、高斯噪声条件下,比 较NSAF算 法、PNSAF算 法、IPNSAF算 法、MPNSAF算法、SSAF算法和ZASSAF算法的性能,仿真结果如图4所示。

图4 各类算法在稀疏系统中高斯噪声条件下下性能比较
由图4可以看出,SSAF算法和ZASSAF算法同样适用于高斯噪声条件下;ZASSAF算法比SSAF算法收敛速度快,且降低了稳态误差。
3.3.3 输入信号为有色信号,各类算法在稀疏信道、非高斯噪声条件下的性能比较
非高斯噪声条件下,稀疏信道信道为图2(a)。非高斯噪声具有较强的脉冲性,严重影响了基于l2范数优化准则的自适应滤波算法的性能,如PNSAF算法、IPNSAF算法和MPNSAF算法。而SSAF、ZASSAF对脉冲噪声具有良好的抑制作用,仿真结果如图5所示。
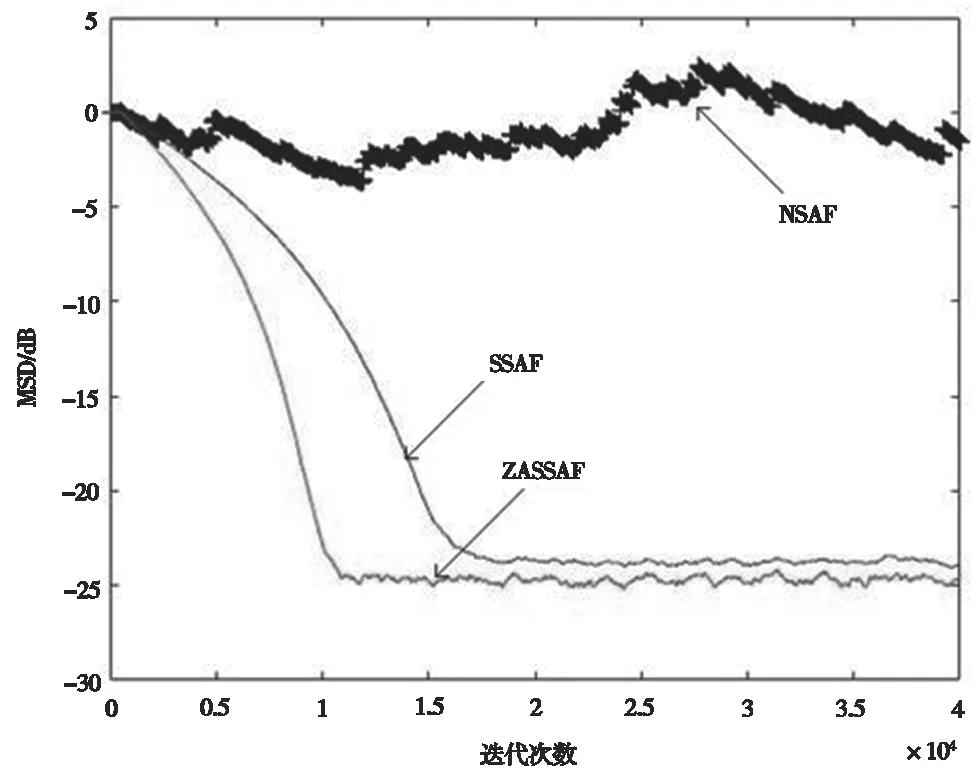
图5 各个算法在稀疏系统中非高斯噪声条件下性能比较
由图5可以看出,NSAF算法在稀疏信道非高斯噪声条件下无法收敛;ZASSAF算法则同时兼顾稀疏系统和非高斯噪声干扰仍迅速收敛。
3.3.4 输入信号为语音信号,算法在稀疏信道中,背景噪声为高斯噪声和非高斯噪声的性能比较
输入信号为语音信号,稀疏信道为图2(a)。图6为存在高斯噪声条件下的收敛曲线,图7为存在非高斯噪声条件下的收敛曲线。可以看出,不同背景噪声下,算法均具有较好的收敛性能,且在非高斯冲击噪声下ZASSAF算法具有更低的稳态 误差。

图6 高斯噪声条件各算法收敛曲线

图7 非高斯噪声条件各个算法在不同系统的跟踪性能
4 结 语
本文提出的零吸引符号子带自适应滤波算法(ZASSAF)是针对稀疏系统和非高斯噪声干扰对算法性能的破坏提出的。仿真实验表明,加入零吸引的SSAF算法可以适用于现实生活普遍存在的稀疏系统,且具有较快的收敛速度和较低的稳态误差。非高斯噪声的干扰和稀疏信道的普遍存在,使得该类算法的研究十分必要。实验结果表明,本文算法对稀疏系统有较好的适应能力,且对非高斯噪声的抑制能力、收敛速度、稳态性能均优于符号子带自适应滤波算法。

