非协作网络的链路性能状态推断技术研究综述*

张志勇 ， 吴佑珂 ， 刘 方 ， 徐 锐

（1.网络空间安全四川省重点实验室，四川 成都 610041；2.中国电子科技网络信息安全有限公司，四川 成都 610041）

0 引 言

互联网作为网络空间最重要的组成部分，自诞生之初便遵循着端到端设计原则，确保了相关技术得以持续发展和进化。但是，随着网络空间的规模持续增大和各种新技术、新业务的不断涌现，互联网的复杂异构特征愈发突出，网络安全措施日益增强，直接获取目标网络的运行状态难度越来越大。为此，通过研究相关的测量方法，间接感知目标网络的运行状态以识别其中的脆弱区域，进而对目标网络采取更有针对性的行动，以达到攻击、阻断等目的，成为网络安全领域所关注的热点问题之一。

针对目标网络脆弱区域的研究，通常从以下两个角度展开：（1）从单个节点的角度，通过软件与系统漏洞挖掘及分析等技术发现其中的安全漏洞；（2）从网络性能的角度，通过性能测量和推断技术获取目标网络的性能参数，识别其中通信服务质量明显下降的区域。本文调研的内容属于后者，即从网络性能的角度发现、识别目标网络的脆弱区域。网络性能的度量参数包括时延、时延抖动、丢包率和可用带宽等多种性能指标。如果在目标网络内部的路由器、主机中安装相关管理软件，可以直接监控各种性能参数，且准确度较高，但面临可扩展性差、测量数据难汇总的问题。更重要的是，目标网络若处在非协作的运行模式中，测量者无法直接访问、控制目标网络的内部节点。因此，需要重点考虑目标网络非协作场景下，识别目标网络内部的性能脆弱区域。

端到端测量通过在目标网络的边缘接入可控的测量节点，在这些测量节点之间收发正常的业务数据而获得目标网络的端到端性能参数[1]。这种测量方法只需要使用目标网络中路由器基本的存储转发功能，对目标网络的依赖性非常小，但是不能直接获得目标网络中各链路的性能参数，还需对端到端测量结果做进一步处理。借鉴医学、地质学中采用层析成像技术（也被称为断层扫描技术）可以对探测目标进行端到端测量而推断其内部状态的思路，网络层析成像技术（Network Tomography，NT）应运而生。它是一种针对计算机网络展开研究，根据对目标网络进行端到端测量获得的数据推断其内部链路性能参数、拓扑结构等参数的方法[2]。由于它能够在不需目标网络内部节点协作的情况下获得其内部性能参数，与当今互联网非协作、异构化、基于边缘控制的特征非常契合，因此是近年来备受关注的一种网络测量技术。本文介绍网络链路性能参数的层析成像方法，通过分析现有方法在达成识别目标网络脆弱区域目标时的优势和不足，提高对相关方法的认识。

1 概念及模型

网络层析成像技术将被测网络视作“黑盒”，不直接在其内部进行测量，仅在网络边缘接入部分探测节点，然后在探测节点之间主动发送探测数据或者被动收集已有数据，从而获得端到端性能参数的测量样本，根据网络拓扑模型和性能参数模型，采用统计学习方法推断网络的内部性能参数。 图1描述了网络层析成像方法的基本理念。

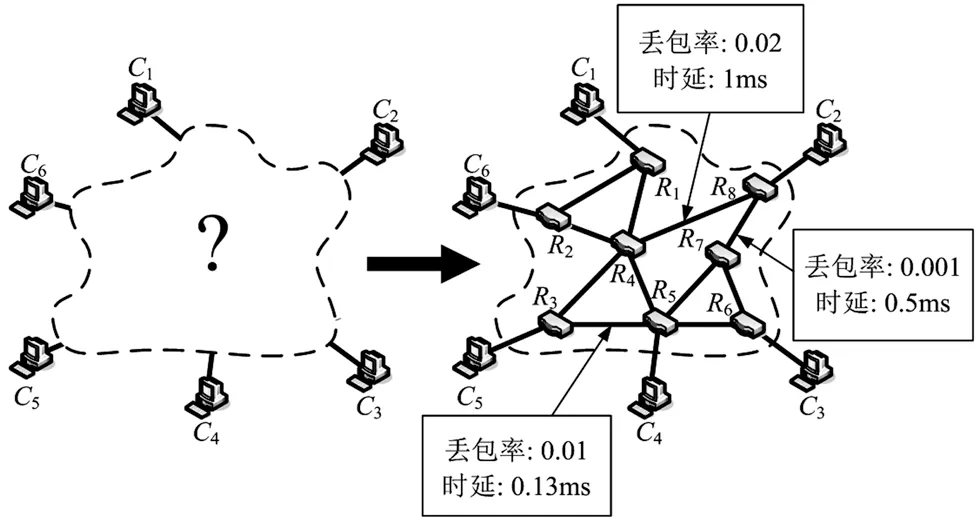
图1 网络层析成像的基本理念

1.1 节 点

通常将设备{R1,…,R8}称为内部节点，这类节点可能因为某些原因无法参与测量，如测量人员无法获得它们的访问权限。将{C1,…,C6}称为边缘节点或者端节点，这类节点是测量人员可以控制的设备，能直接参与端到端测量。值得注意的是，网络层析成像研究中的节点是抽象概念，不仅可以表示路由器、主机等单个设备，也可以代表一个局域网甚至一个AS自治系统。

1.2 链 路

在网络层析成像研究中，链路是一个抽象的概念，指的是两个直接相连的节点之间的连接关系，不只是表示这两个节点之间的物理链路。比如，网络层析成像研究的链路时延，并不是数据报文在传输介质中的传播时延，而是指它在节点缓冲区中的排队时延。由于两个节点之间有两个传输方向，而且数据在这两个方向上的传输性能存在差异，因此网络层析成像研究的链路通常是有向链路。图1中，节点C1和R1之间实际上存在两条有向链路（不妨将其记为lC1→R1和lR1→C1）。在少数文献中，出于简化问题或者其他因素的考虑，也会认为链路不存在方向[3]。

1.3 路 径

任意两个节点之间的连接关系用路径表示，网络中的某个节点向另一个节点发送数据时，数据包经过的路由就是该节点到另外那个节点的路径。通常情况下，一条路径是一个有向无环的链路序列。特别地，称两个端节点之间的路径为端到端路径。当网络采取基于最小跳数的路由策略时，图1中节点C1和C6之间的端到端路径由lC1→R1，lR1→R2，lR2→C6等三条链路组成。

1.4 拓扑模型

假设网络中路由稳定，当给定一个端节点作为发送测量数据的源节点，其他端节点作为接收测量数据的目的节点时，所有测量数据经过的路径会形成一个树状结构。比如，以图1中的C6为源节点，{C1,…,C5}为目的节点时，各路径形成的树状网络如图2（a）所示。为了简化问题，大多数网络层析成像方法都围绕这样的树状网络展开。实际上，任意结构的网络拓扑都可以被认为是若干个树状拓扑的组合。

端到端路径和链路之间的关系可以用一个元素取值为0或者1的二进制矩阵表示，称之为路由矩阵。设R为某网络的路由矩阵，那么它的每一行对应一条端到端路径，每一列对应一条链路。如果第i行对应的端到端路径经过第j列对应的链路，那么R中第i行j列的元素R(i, j)=1，否则R(i, j)=0。

1.5 参数模型

对于某些性能参数（如时延），端到端路径的性能参数是它经过的所有链路的性能参数之和。借助路由矩阵，可得到网络层析成像的基本数学模型为：

其中，Y代表路径级的测量数据，X代表待估计的链路级数据，ε表示测量数据中的噪声，R反映端到端路径和内部链路之间的路由关系。基于网络层析成像的拓扑识别研究是在已知Y的条件下，估计R；基于网络层析成像的链路性能参数估计研究，则是在已知Y和R的条件下，求解X。

当路由矩阵R中某两列相等即网络中存在某两条链路，经过它们的端到端路径集合完全相同时，根据线性代数的知识可知，不可能将这两列对应的待求参数区分开。在网络层析成像中，称这样的链路不可辨识，如图2（a）中的lR2→R1和lR1→C1。为了避免这个问题，网络层析成像方法首先将所有相互不可区分的链路合并为一条虚拟链路，称之为逻辑链路。图2（b）是对图2（a）中的网络进行处理后得到的逻辑拓扑。若无特别说明，后文中提及的“网络拓扑”均指网络的逻辑拓扑。

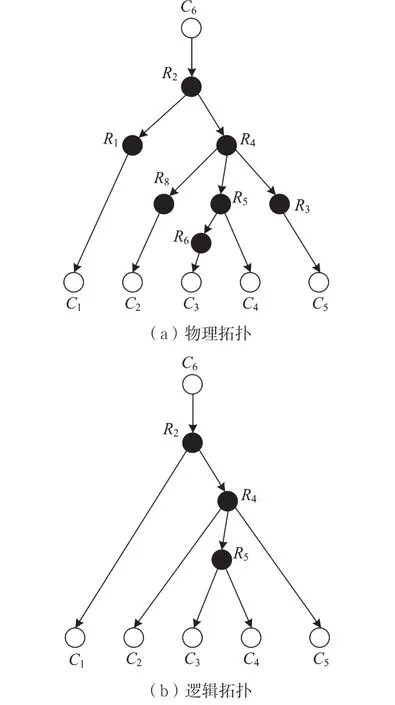
图2 树状网络的物理拓扑和逻辑拓扑

2 链路性能状态推断

下面将从定量参数估计和定性参数估计两个方面介绍现有研究情况。对于定量参数估计问题，性能参数主要包括链路时延和链路丢包率。链路时延本身是一个取值为正实数的随机变量，常对其分布进行估计。而链路丢包率可被视为链路时延超过某个门限的概率，是需要直接估计得到的参数。定性参数估计通常将链路丢包率和一个预设门限进行比较，转化为取值为0或者1的二元随机变量。当链路的丢包率高于门限时，称其为拥塞链路。因此，该问题也常被称为拥塞链路识别。

2.1 链路时延估计

链路时延估计通常是指根据端到端数据推断链路排队时延的分布，包括参数化方法和非参数化方法两类。

2.1.1 参数化方法

参数化方法采用某种特定分布近似链路的时延分布，其模型参数的数目是固定的。参数化方法使用的近似分布模型包括连续分布模型和离散分布模型两类。

（1）基于连续分布模型的链路时延估计方法

美国密歇根大学的M.Shih和A.Hero采用有限混合模型对链路时延的概率密度函数进行建模[4]：

其中，fl(x)为链路l时延的概率密度函数，是kl个子成分的概率密度函数的凸组合；αl(m)是第m个子成分的权重；g(x;θl(m))是其概率密度函数，由参数θl(m)决定。各个子成分可以是指数分布、高斯分布等特定类型的分布。比如，当子成分为高斯分布时，θl(m)=(ul(m),σl(m))，其中ul(m)和σl(m)分别表示均值和标准差。根据背靠背单播包的测量数据，M. Shih和A.Hero采用期望最大化（Expectation Maximization，EM）算法估计出式（2）中的αl(m)和θl(m)等参数。美国佛罗里达大学的Y.Xia等人的研究表明，混合指数模型能够相对准确地逼近链路时延的真实分布[5]。

（2）基于离散分布模型的链路时延估计方法

基于连续分布模型的链路时延估计方法用特定分布逼近链路时延的真实分布。当近似分布和实际分布相差较大时，最终的估计结果存在很大偏差。为了更好地逼近链路时延的真实分布，需要采用一些比较复杂的模型，又会增加问题的复杂性。为了克服这些不足，很多文献将连续的路径时延和链路时延量化到一组离散状态集合中，然后估计链路时延离散状态的概率质量函数（Probability Mass Function，PMF）[6-9]。

根据离散化过程中采用的量化间隔（BinSize），目前有两种常用的离散模型，分别采用固定量化间隔和可变量化间隔。其中，量化间隔可变的离散模型实质上是由若干个基于固定量化间隔的离散模型组合而成。它采用不同粒度刻画不同区间的时延，能够在保持精度的同时以较少的离散状态描述链路时延[8-9]。例如，图3中量化间隔可变的离散模型实际上是由间隔长度分别为q和3q的两个离散模型组合而成。它用细粒度的离散状态刻画较小的时延，用粗粒度的离散状态刻画较大的时延，共需 9个离散状态，而仅以q为量化间隔的离散模型需要15个离散状态。这种模型的不足之处在于，为了保证链路离散状态之和等于路径离散状态之和，需要同时计算链路时延在多个量化间隔（比如图3中的q和3q）下的PMF。

图3 离散时延模型

在离散时延模型下，链路时延PMF和路径时延PMF之间存在卷积关系。F. L. Presti等人采用一种递归计算方法模拟反卷积过程，从最小时延状态开始建立链路时延PMF的多项式方程再对其求解[6]。 这种方法实质上是一种基于矩估计的方法，对测量数据的利用率不如最大似然估计（Maximum Likelihood Estimate，MLE），在某些场景中估计精度不太理想[10]。E.Lawrence等人采用EM算法在多播树中求解链路时延分布的最大似然估计，能够取得较高精度[7]。但是，EM算法的计算复杂度通常很高，很难推广到大规模网络中。G.Liang等人对这个问题进行改进，将初始的树状网络划分成多个子树，忽略了各个子树之间的相关性，将全局最大似然估计问题转化为多个子问题的最大似然估计问题，进而获得链路时延的最大伪似然估计[11]。

2.1.2 非参数化方法

非参数化方法是指模型参数的数目或者自由度随着测量数据动态变化。Y. Tsang[12-13]等人用背靠背包进行端到端测量，以基于固定量化间隔的离散时延模型为基础，将离散状态数设定为 K =■l og2N■。 其中，N是背靠背探测包的组数，表示向上取整函数。当测量数据存在误差时，增加状态数目会使离散时延模型刻画链路时延时存在过拟合现象。于是，他们提出了一种多尺度最大惩罚似然估计方法（Multiscale Maximum Penalized Likelihood Estimation，MMPLE），在一般似然函数的基础上增加一个惩罚因子，避免了似然函数对测量数据的过度拟合。若令y为离散化的路径时延，p为所有链路时延的PMF，MMPLE方法的本质是求解式（3）的最优化问题：

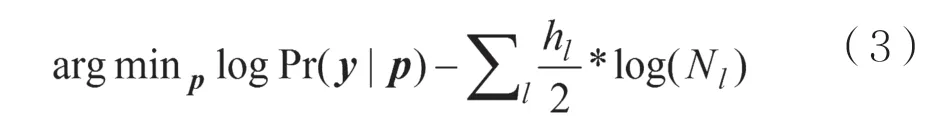
其中，logPr(y|p)是以p为参数、y为观测数据的对数似然函数。惩罚因子中，Nl表示经过链路l的背靠背包数目，hl表示链路l的时延PMF的非零哈尔小波系数个数。求解问题（3）的过程和小波除噪的过程非常类似，因此MMPLE用普通的EM算法进行迭代，在每一轮迭代中获得一个初步的链路时延PMF，然后对其进行哈尔小波变换，仅保留系数高于某门限的分量，从而获得这一轮迭代中链路时延PMF的估计值，作为EM算法中下一轮迭代的初值。

不同于上述方法直接估计链路的时延分布，M.Shih等人提出了首先估计链路时延的累积量生成函数，然后根据累积量生成函数获取时延分布的间接估计方法[14]。当不同链路的时延相互独立时，路径时延的累积量生成函数等于该路径上所有链路的时延累积量生成函数之和，因此可以建立和式（1）类似的线性方程组。其中，参数Y和X分别对应路径和链路的时延累积量生成函数。为了解决欠定性问题，M. F. Shih等人对部分链路直接测量，以减少未知变量数目。但是，对链路时延直接测量存在困难时，该方法会受到限制。G. Antichi和G. Fei等人分别提出了链路时延高阶累积量的估计方法[15-16]。基于估计得到的累积量，可以在不对链路时延作任何假设的情况下，采用Edgeworth级数或鞍点法逼近链路时延。

美国贝尔实验室的A.Chen等提出根据时延分布的特征函数间接估计链路时延分布的方法[17]。令随机变量Xl表示链路l的时延，Xl的特征函数定义如下：

其中，fXl(x)是Xl的概率密度函数，对其进行傅立叶变换即可得到相应的特征函数φXl(t)。

因为当各条链路的时延相互独立时，路径时延的概率密度函数等于该路径上所有链路时延的概率密度函数的卷积，所以路径时延的特征函数等于相应链路时延特征函数的乘积。根据这一关系建立链路和路径时延特征函数的方程，利用最小二乘法对其求解。该方法的本质是寻找一个链路时延分布的估计值，使得由相应链路时延特征函数计算得到的路径时延特征函数能够尽可能逼近测得的路径时延特征函数。

2.2 链路丢包率估计

链路丢包率估计问题可以被视为仅有两个离散状态的链路时延估计，但因其特殊性，通常对它单独进行研究。根据采用的丢包模型，现有方法可以分为基于链路丢包时域独立和时域相关的两种估计方法。为了描述方便，通常将丢包率转换为成功传输率（即1减去丢包率）进行处理。

2.2.1 基于链路丢包时域独立的估计方法

这类方法用Bernoulli过程描述链路的丢包事件，认为同一链路上的数据包相互独立，链路在不同时刻发生丢包的概率相等。

在基于多播测量的链路丢包率估计研究中，美国AT&T实验室的R. Caceres等人作出了开创性的工作[18]。在树状网络中，除根节点s外，每个节点k都有唯一的上一跳，称其为k的父节点并用F(k)表示。用pk表示F(k)到k的链路的成功传输率，qk表示根节点s到k之间的路径的成功传输率。当不同链路的丢包相互独立时，式（5）成立：

根据多播探测包的特点，可为每个内部节点k建立一个以qk为未知变量的高次多项式方程，该方程的次数恰好等于k的子节点数目。根据这些方程解出qk和qF(k)后，由式（5）可以直接获得pk的估计值。理论分析表明，该估计值是pk的最大似然估计。

当多项式方程的阶数大于4时，需要采用一般化的数值方法对其求解，求解过程比较繁琐。为了克服这个问题，N. Duffield、H. Su等人分别提出了获得pk的显式估计器，从而降低了估计算法的计算复杂度[19-20]。

美国马萨诸塞州大学的T.Bu等人对具有一般拓扑结构的网络链路丢包率估计问题进行研究[21]。他们将一般拓扑视作多个树状网络的组合，在每个树状网络中进行多播测量，然后提出两种方法对链路丢包率进行估计。第一种方法首先在每个树状网络中求得其中各条链路的成功传输率，然后以各条链路在不同树中的估计结果的最小方差加权平均值（Minimum Variance Weighted Average，MVWA）作为最终的估计结果。第二种方法则直接在一般网络中使用EM算法，以迭代的方式逼近链路丢包率的最大似然估计。相较于MVWA，EM算法的估计结果更接近最大似然估计方法的全局最优解，通常具有更高的精度。

以上链路丢包率估计方法都基于多播测量方式，而M.Coates等人提出了基于背靠背单播包测量的链路丢包率估计方法[22]。背靠背包实际上是利用两个连续的单播包对多播包进行模拟，在两个包经过的公共链路上，第一个包被成功传输的条件下，第二个包也被成功传输的条件概率γ非常接近1。 当γ=1时，背靠背包和多播等价。但是，由于实际网络中背景流量的干扰，γ通常小于1。此时，若仍然按照基于多播测量的估计方法估计链路丢包率，得到的结果可能存在较大误差。为此，同时将链路丢包率和条件概率γ作为待估参数，采用EM算法获得它们的最大似然估计。

2.2.2 基于链路丢包时域相关的估计方法

考虑到实际网络中链路丢包具有突发性，如果某个数据包被丢弃，那么它后面的数据包也可能以较大概率被丢弃，这一性质被称为链路丢包的时域相关性。Bernoulli过程无法反映链路丢包的时域相关性，因而不够准确。

美国哥伦比亚大学的D. Guo等人采用Gilbert模型描述链路丢包过程[23]。Gilbert模型实质上是一个二阶马尔科夫链，如图4所示。其中，p是当前数据包被成功传输的条件下下一个数据包被丢弃的概率；类似地，q是当前数据包被丢弃的条件下下一个数据包被成功传输的概率。最后，采用基于Gibbs采样的贝叶斯估计方法，可获得Gilbert模型的参数p和q。

图4 Gilbert模型

M. Yajnik等通过分析真实网络的测量数据，指出k阶马尔科夫链（k-th order Markov Chain，k-MC）可以更准确地描述链路丢包过程，优于Bernoulli模型和Gilbert模型[24]。基于此，费高雷等人将Gilbert模型推广到一般情况，采用k-MC对链路丢包过程建模，分别采用最大伪似然方法和约束最优化方法估计k-MC的状态转移概率[25]。

澳大利亚墨尔本大学的V. Arya等人将上述方法推广到链路丢包时域相关的场景下，能够估计链路连续丢弃多个包的概率[26]。他们还采用一种子树划分的思想，避免对高次多项式方程求解，降低了计算复杂度。这种子树划分的思想也可以用在链路丢包时域独立的场景下，以便快速求解链路丢包率。同时，他们还将该思路推广到链路时延时域相关的场景下，用来估计链路时延的一些时域特征参数，如链路时延大于某个门限的平均持续时间。

2.3 拥塞链路识别

诊断、定位网络内部的拥塞链路是网络测量的一项重要任务。利用网络层析成像技术诊断拥塞链路的思路有两种。第一种是利用链路性能参数的定量估计方法，借助测量数据的“报文级”相关性直接估计网络内部链路性能参数的具体值，然后识别低性能链路；第二种是借助测量数据的“性能级”相关性，判断网络内部各条链路的性能参数是否满足某个特定要求，将不满足要求的链路识别为拥塞链路。后一种思路最早由美国学者N.Duffield和V. Padmanabhan独立提出。它涉及的端到端测量过程非常简单，因此受到了人们的广泛认可，并逐渐成为拥塞链路识别的主流方法。若无特别说明，后文提到的拥塞链路识别方法均指第二种方法。

根据测量过程是否被划分为多个时隙，现有的拥塞链路识别方法可以大致分为基于单时隙测量和多时隙测量的方法。

2.3.1 基于单时隙测量的拥塞链路识别

V. Padmanabhan等人用丢包率作为衡量链路是否拥塞的性能指标，提出了3种估计链路丢包率近似值的方法：线性最优化、随机采样和基于Gibbs采样的贝叶斯估计[27]。线性最优化方法以路径传输率和链路传输率的对数之间的线性关系为约束，链路传输率的对数和为最小化目标，建立一个约束最优化问题并对其求解。随机采样方法根据路径丢包率与链路丢包率之间的关系确定链路丢包率的大致取值范围。在该范围内随机采样，获得各条链路的丢包率样本，然后以样本均值作为链路丢包率的估计值。基于Gibbs采样的贝叶斯估计方法则利用比较成熟的Gibbs采样方法生成一个马尔科夫链，使得该马尔科夫链的稳态分布正好是链路丢包率的后验分布。因此，Gibbs采样过程稳定后所生成的样本服从链路丢包率的后验分布，这些样本的均值可被视为链路丢包率的后验估计。

以上三种方法中，随机采样方法的采样过程比较粗糙，因而估计精度在三者中最差。线性最优化方法则存在对测量误差敏感的问题，为此H. Lim及H. Song等人从降低测量误差和改进最优化问题等角度对该方法加以改进，取得了较好的效果。基于Gibbs采样的贝叶斯估计方法直接利用端到端数据中各条路径成功传输的报文数而非路径的成功传输率，因此在测量样本较少时也能取得较高精度，但它的计算复杂度非常高，很难推广到大规模网络中。哈尔滨工业大学的杨京礼博士利用网络中部分链路的丢包率可由线性方程组唯一确定的特征，首先求解确定性链路的丢包率，然后采用Gibbs采样方法估计非确定性的丢包率。这种方法减少了Gibbs采样过程的变量数目，能够有效降低计算复杂度。

N. Duffield建立了一个用于诊断拥塞链路的网络层析成像理论新框架[28]。由于该框架建立在布尔代数域，因此通常称之为“布尔网络层析成像”或者“二进制网络层析成像”。在该框架下，链路和路径的性能参数首先被映射为“正常”或者“拥塞”两个状态（分别用0和1表示），然后根据链路性能参数模型的“可分离性”导出链路状态和路径状态之间的关系：一条路径是正常的，当且仅当它经过的所有链路都是正常的。基于该框架，N. Duffield针对树状网络提出了一种快速而简单的算法SCFS（Smallest Consistent Failure Set algorithm）。

SCFS利用网络中拥塞链路占少数的特点，寻找尽可能少的拥塞链路解释观测到的拥塞路径。在树状网络中，将所有正常路径经过的链路移除后，原始网络将被划分为多个拥塞子树。SCFS将这些子树的根链路判定为拥塞链路，其他所有链路判定为正常链路。图5是SCFS的操作示意图，其中正常路径经过的链路用虚线表示，斜体数字表示链路或者路径的状态。

图5 SCFS算法

SCFS算法的思想很容易推广到一般结构的网络中。美国佐治亚理工学院的A. Dhamdhere等人指出，在非树状网络中寻找能够解释拥塞路径的最小拥塞链路集合实际上是一个集合覆盖问题，采用贪婪策略可以求得其近似最优解[29]。瑞士洛桑理工学院的H. Nguyen等人注意到，在某些网络场景下，链路性能参数并不严格满足“可分离性”，会导致端到端数据中存在测量误差[30]。为了克服这一问题，他们从最大后验准则出发，推导出修正测量误差的最优化目标，然后采用一种启发式方法对路径状态进行修正，再调用SCFS算法识别拥塞链路。

佐治亚理工学院的S. Zarifzadeh等人结合传统层析成像方法和布尔层析成像方法的优点，提出了一种名为RangeTomography的框架[31]。在该框架下，他们不仅能够识别出链路状态，而且在得知链路拥塞时，能够估计出链路丢包率的大致范围，从而获取链路的具体拥塞程度。

2.3.2 基于多时隙测量的拥塞链路识别

多数基于单时隙测量的拥塞链路诊断方法都基于一个假设：网络中所有链路的先验拥塞概率相同且小于1/2。这个假设在实际网络中不一定成立，因而会降低诊断结果的准确性。

H. Nguyen等人在布尔网络层析成像的框架下证明了链路的先验拥塞概率可以通过多个测量时隙的数据唯一确定，并提出一种基于矩阵求逆的方法对其求解，然后将链路的先验拥塞概率和后续测量时隙的端到端数据结合，根据最大后验准则，求得链路状态的最大后验估计[32]。相较于SCFS算法，这种方法的准确度更高。特别是当网络中拥塞链路较多时，它具有更高的检测率。洛桑理工学院的D. Ghita等人将上述方法推广到更一般的场景中[33-34]，发现并证明了网络中某些链路的状态不相互独立时，链路先验拥塞概率可辨识的充要条件，并提出一种只需对少量端到端路径进行测量即可求得链路先验拥塞概率的方案。这项工作扩展了故障链路诊断方法的适用范围。

此外，H. Nguyen和D. Ghita等人利用链路传输率和路径传输率的线性模型直接求解链路传输率的近似值[35-36]。这种方法的求解目标和前文提及的最优化方法类似，不同之处在于他们认为链路丢包率的方差和相应的丢包率成正比，丢包率方差小的链路相应的丢包率也小。由多个测量时隙的路径丢包率方差估计出链路丢包率方差后，他们在后续时隙中将方差小于某门限的链路丢包率近似为0，再求解其他链路的丢包率近似值。该方法的本质是在保持端到端路径数不变的情况下，通过减少链路数目来解决链路丢包率估计的欠定性问题。

除了上述单纯通过端到端测量诊断拥塞链路的层析成像方法外，还存在一种将端到端测量与诊断、修复拥塞链路过程相结合的方法。这种方法最早由N.Duffield提出，基本思路是根据路径状态推断一个疑似拥塞的链路集合后，对这些链路单独进行测量，以确认它们是否确实拥塞[28]。比如，在每个测量时隙中运行SCFS算法获得拥塞链路集合后，对该集合中的链路分别检验、修复（若该链路确实拥塞），直到端到端路径的测量状态表明网络中所有链路都正常。

通常情况下，某一条疑似拥塞的链路被确诊为拥塞并将其修复后，在下一个时隙中应该是正常的。换言之，已经被修复的链路的状态在后续时隙中可以作为诊断其他疑似拥塞链路的已知信息，因此不同的诊断顺序对应的成本也将不同。美国哥伦比亚大学的P. Lee等人指出，优先对拥塞概率最大或者诊断成本最小的链路进行检验，并不能使整体的诊断成本最小[37]。他们为每条链路构造一个特征函数，并证明了最优诊断策略应该优先诊断特征函数值最大的链路。

美国康涅狄格大学的B.Wang等人提出一种序贯检测的思路，要求优先被检测的链路满足以下性质[38]：在已知该链路的状态后，将它的状态和端到端数据结合，能够确定尽可能多的其他链路状态。相比其他方法，该方法在每个时隙中确定多条链路的状态，收敛速度更快。

3 结 语

采用网络层析成像技术推断目标网络的链路性能状态，从性能的角度识别该网络内部的脆弱链路，能够有效克服对目标网络缺乏访问控制权限的难题。现有研究主要集中在链路时延分布、链路丢包率估计和拥塞（低性能）链路识别等三个方面。其中，前两者的目标参数定义域为某个连续的实数区间，需要利用报文级的相关性将每个探测报文均视作一个样本，因此必须采用特殊的探测方式。而后者的目标参数被转化为二元变量，仅需利用性能级相关性，可采用普通单播包作为探测手段。推断过程中，以上问题的思路则保持一致，通过建立端到端路径性能参数和链路性能参数之间的统计关系模型，再采用各种推断方法学习获得该模型的未知参数，即内部链路性能参数。事实上，当对目标网络进行持续探测时，结合后续观测得到的路径性能参数和已经估计得到的链路性能参数，可以用于预测后续的链路性能状态，形成“学习→预测”的全套流程。