一种基于APSK非均匀差错保护的非均衡编码方案*
刘希文,许 吉,程 晨
(1.南京邮电大学 电子与光学工程学院 微电子学院,江苏 南京210046; 2.深圳市中兴微电子技术有限公司智能互联产品部,江苏 南京 210000)
0 引 言
随着社会的发展和科技的进步,虚拟现实、高清视频通话等新兴应用出现,大大丰富了人们的生活,但这些应用依赖于通信质量,对通信系统的信息速率具有很高的需求。为满足需求,对通信系统的调制方式而言,高阶调制的应用成为大势所趋,这是因为高阶调制相比传统的低阶调制具有更好的频谱利用率,可以带来更高的信息速率。
APSK是一种高阶的幅度与相位联合调制技术,具有独特的星型星座结构,因此具备优良的抗非线性失真能力,非常适合卫星通信等非线性信道环境。当前,采用LDPC纠错编码对APSK调制进行差错控制已经屡见不鲜,LDPC结合APSK的编码调制系统展现出了较优良的误码率性能,如第二代数字卫星广播标准、中国宽带电力线通信标准化白皮书等标准文件中均使用了这一调制编码系统。
但是,传统的LDPC编码-APSK调制系统依然存在一个问题:2m-APSK对于映射到每个符号点上的m个比特具有不均等的差错保护,因此一部分受到低程度保护的比特会降低LDPC码的译码性能,使得系统整体误码率恶化。针对这一问题,国内外学者已经进行了一些研究,当前主流的做法是采用多级编码(Multilevel Codes,MLC)[1]来对保护不均等的比特进行不同程度的LDPC差错控制。2004年JiaHou[2]等人将MLC引入比特交织编码调制系统,在低阶的8PSK调制下具有不错的误码率性能,但并未探究其在高阶调制中的可行性;2015年Daiki Yoda[3]等人针对APSK设计了一种改进的MLC方案,进一步提升了LDPC-APSK系统的误码性能,但由于采用了多级译码(Multi-stage Decoding,MSD)的译码方式,即便经过了优化依然会带来系统延时。因此,本文设计了一种适用于高阶APSK的非均衡LDPC编码方案。与MLC方案不同,本方案在不产生延时的前提下对APSK不同保护程度的比特使用了不同码率的LDPC码进行编码,且通过MATLAB对该方案进行了建模仿真,验证了该方案对通信系统整体误码性能的提升。
1 APSK的非均匀差错保护分析
APSK的星座图由不同数量的同心圆组合而成,每个同心圆上分布着一定数量的PSK信号点。在基于APSK调制的通信系统中,数据发送端对信息比特进行APSK调制,数据接收端将接收到的信号进行APSK解调恢复成为比特信息。信号的调制过程是将每连续的m个比特映射为星座图上一个2m阶APSK星座点,而对于解调过程,由于绝大部分译码器都需要解调器提供每个比特的软信息即对数似然比(Log Likelihood Ratio,LLR),因此软解调模块需要根据接收到的信息y计算每个比特的LLR,这个过程称为APSK软解调。
设定信道模型为加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道,用bi,k表示APSK已调信号中第i个符号的第k个比特,其LLR计算式为:
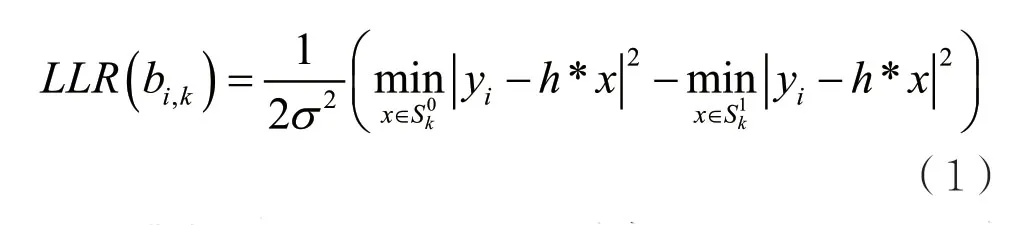
式中Sk1和Sk0分别表示星座图上第k个比特为1和0的所有符号点的集合,σ2表示高斯白噪声的方差,h则表示信道增益。
式(1)通常被称为max-log-map算法[4]。不难看出,软解调算法需要计算接收符号到集合Sk1和Sk0中所有点的距离并进行比较。这些第k个比特为“1”和“0”的符号点在星座图上各自连成了一片区域,区域之间的区分边界被称为判决边界。由于APSK的星型结构,APSK符号中不同比特的判决边界各不相同,决定了APSK对不同比特的差错保护程度是不均匀的。
以64-APSK为例,采用文献[5]中定义的均匀64-APSK星座图进行分析,如图1所示。
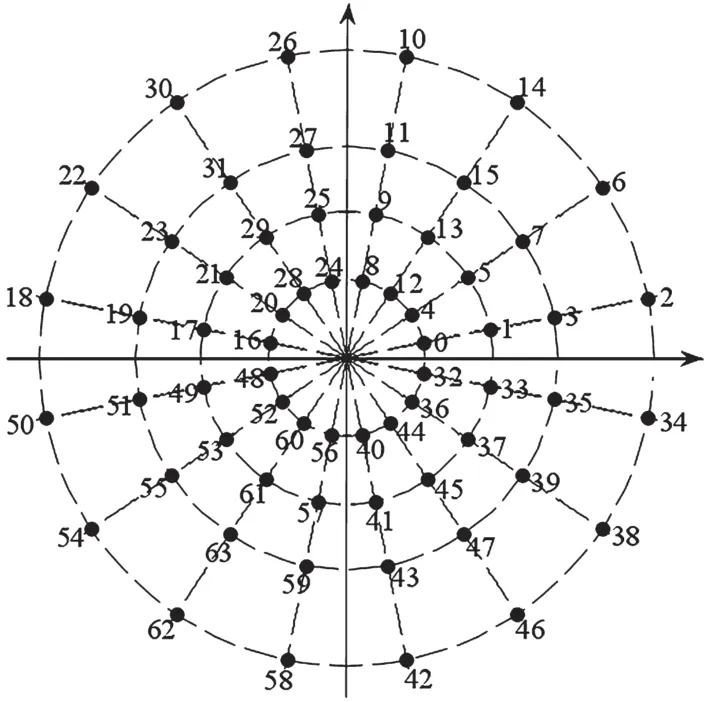
图1 64-APSK星座图
该星座图参数如下:星座图包含4个同心圆环,经过能量归一化后,从内环到外环半径依次为R1=0.381 8、R2=0.716 4、R3=1.034 8和R4=1.506 7,每个圆环上均匀分布着8个符号点。以b1、b2、b3、b4、b5和b6表示映射到一个APSK符号上的6个 比特,顺序为从高位到低位,根据6个比特表示的信号参量的不同,可以将它们划分为相位比特和幅度比特两类:b1、b2、b3、b4为相位比特,表示APSK已调信号的相位参数;b5和b6为幅度比特,表示APSK已调信号的幅度参数。它们的判决边界如图2所示。
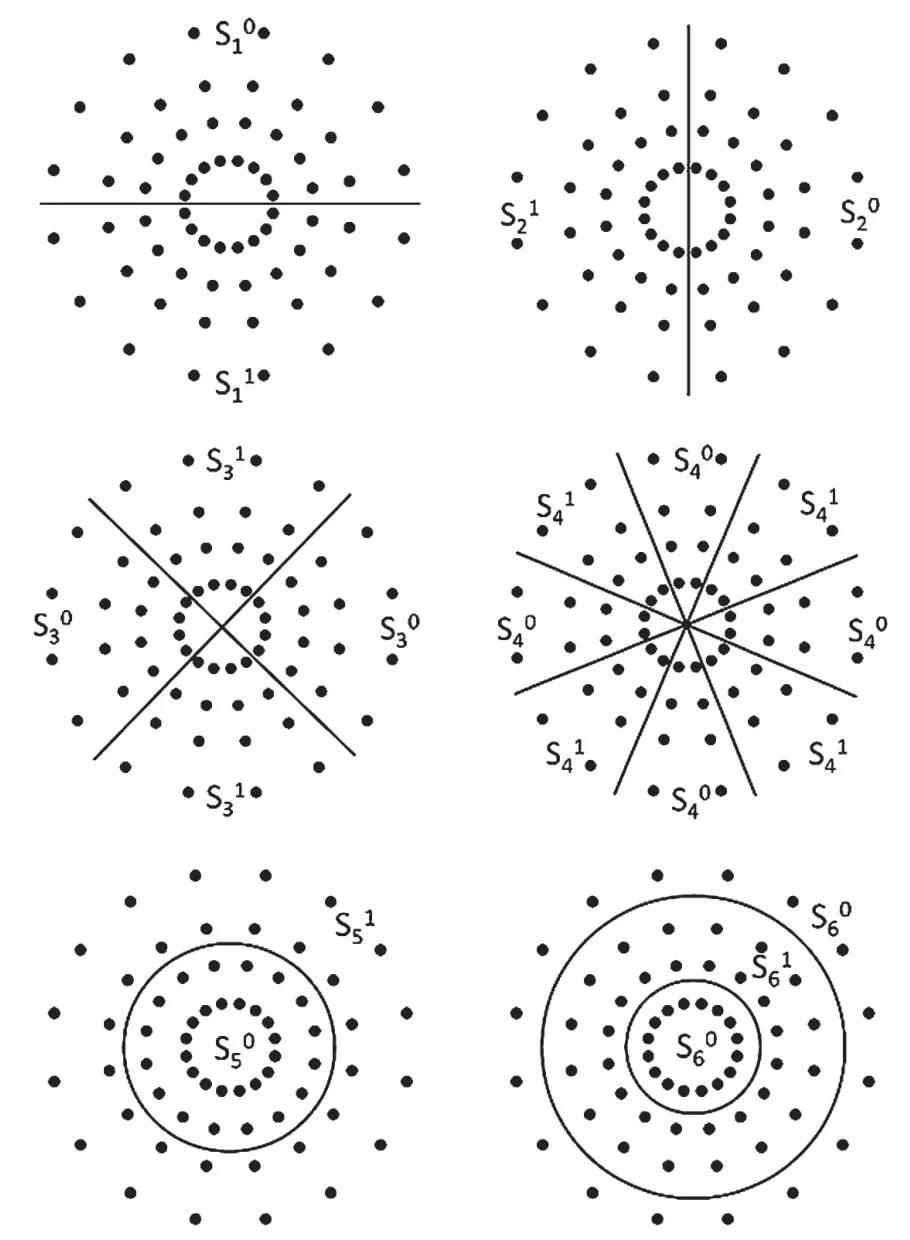
图2 64-APSK的判决边界示意
信号传输经过信道后,由于噪声等因素的干扰,接收端接收到的符号点会发生偏移。由式(1)可知,一旦符号点偏移越过判决边界,计算的LLR信息符号就会出错,导致判决结果出错[6]。一个比特的判决边界越复杂,符号点发生偏移后越过判决边界的概率越高,判决时就越容易出错。APSK对于该比特的保护程度相对较低,文献[3]和文献[6]中通过APSK星座点的最小欧氏距离对这一现象进行了理论分析;本文利用MATLAB对64-APSK调制解调系统进行了定量仿真,分别累计了6个比特的误码,如图3所示。
可以看到,对比相位比特,b4比特的误码性能明显最差,b1和b2比特的误码性能基本相同,优于其余2个比特。结合判决边界示意图可以分析其原因:b4比特的判决边界最复杂,将整片星座图划分为8个区域,噪声的干扰很容易使得符号点偏移越过边界,因而b4受保护程度最差;b1和b2判决边界均为穿过圆心的一条直线,仅仅将星座图分为了对称的两个空间,因此受保护程度相同且最强。
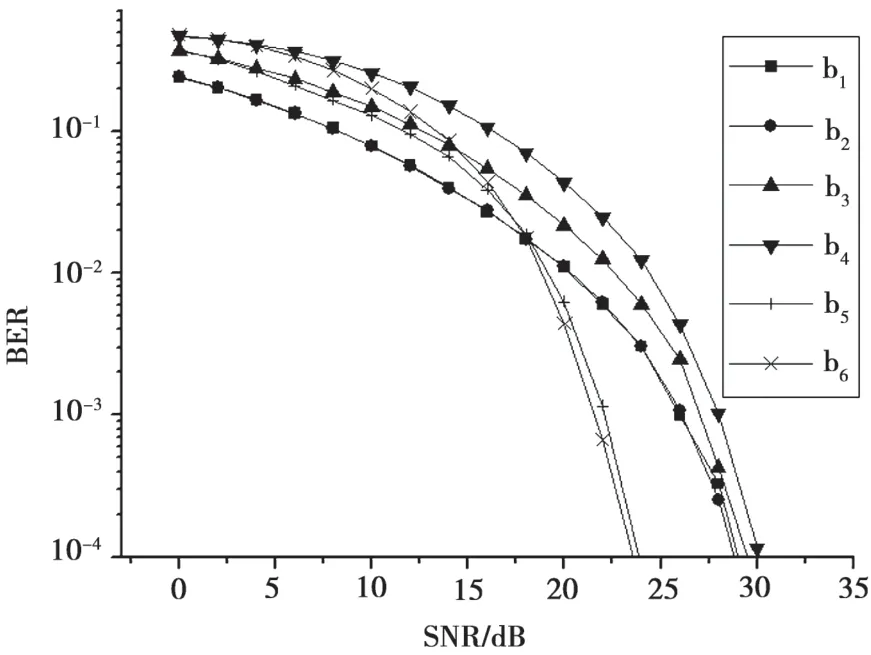
图3 64-APSK各比特的误码率-信噪比
对比幅度比特,在信噪比较小的区间,如图4所示,b6比特的误码率明显高于b5比特。随着信噪比的增加,b5和b6两个比特的误码率渐渐趋向一致,且误码性能开始优于其他4个相位比特。在误码率为10-4时,已经优于相位比特约7 dB。造成这一现象的原因是:幅度比特的判决边界均为环形,b6的判决边界比b5多出一个环,因而在噪声干扰较大时更易出错;随着信噪比的升高,符号点在星座图上的偏移量变小,很难越过幅度比特的判决边界;同时,由于最内环相邻信号点之间欧式距离最短,因此此时内环相邻点间的相互干扰成为产生误码的主要来源,所以相位比特误码率要比幅度比特误码率下降速度更慢。综上所述,MATLAB的仿真结果与文献中的理论分析基本一致,且更加直观定量地呈现了APSK的非均匀差错保护。
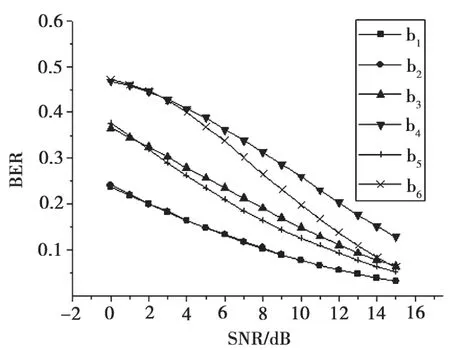
图4 64-APSK在0~15 dB的误码率-信噪比
在实际的通信系统中,除了进行映射调制外,还需要对数据进行纠错编码,以大幅提升数据传输的可靠性。低密度奇偶校验码(LDPC)[7]是通信系统中最常用的一种纠错码。
2 非均衡LDPC编码方案
LDPC码凭借逼近香农极限的性能、超高的译码吞吐率以及适合硬件实现等优势,而被广泛应用于卫星通信、无线通信和数据存储等领域[8]。LDPC码的译码性能除了与生成矩阵性能有关外,还与其码率有直接关系。在生成矩阵给定的条件下,码率越低,LDPC码的纠错性能越强,但同时信息速率也越低。因此,在实际应用中,需要评估具体场合对误码性能和信息速率的需求,选择合适码率的LDPC码构建编码器。
在实际的编码调制系统中,编码和调制之间还会增加比特交织模块[9],使得信道上产生的差错随机化,更利于纠正突发性错误。但是,对于LDPC码,由于其本身的稀疏性和随机性,因此只要校验矩阵设计得当,可以认为LDPC码具备了内在的交织性,可以省略交织器[10]。经过LDPC编码器编码后的码字,直接送往APSK调制器,每m个比特被映射到星座图上的一个符号点,系统框图如图5所示。正如上文分析,由于APSK对不同比特的非均匀差错保护,较低保护的比特势必会降低系统整体的误码性能。
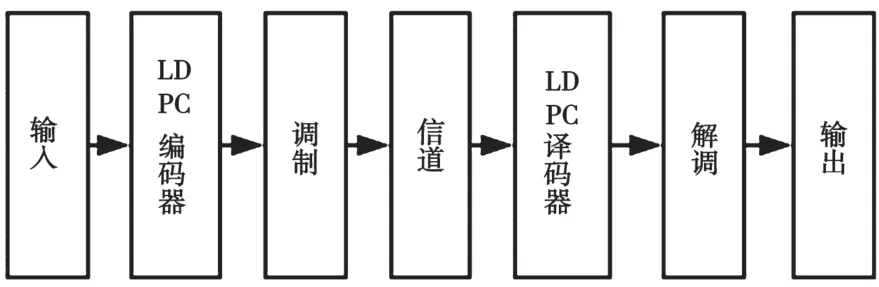
图5 传统的编码调制系统
针对这一现象,在传统的MLC方案中,往往会根据星座图上2m个调制符号相互间的欧式距离,为每一级数据匹配不同的纠错编码。因此,需要m个编码器和译码器才能实现[10]。在高阶调制中,这无疑会带来巨大的硬件开销。
本文提出的非均衡编码方案使用比特交织器,通过交织方式对不同保护程度的比特分别使用不同码率的LDPC码进行匹配。首先根据计算的APSK各比特误码率性能对比特进行分组,然后根据每组的总误码性能匹配相应码率的LDPC码,从而节省硬件开销。例如,在64-APSK中,由图4可见,64APSK对于b4和b6比特的保护程度要低于其余 4个比特。因此,b4和b6比特采用码率较低、纠错能力较强的LDPC码,b1、b2、b3、b4则采用码率相对较高的LDPC码。方案的系统框图如图6所示。
输入的信息比特首先进入串并转换器,根据LDPC编码器的信息位长度分为两路并行且非等长的数据输入两个不同的LDPC编码器。LDPC编码器1采用码率较高的LDPC码,码长为4N,对应调制模块的b1、b2、b3和b5比特;LDPC编码器2采用码率较低的LDPC码,码长为2N,对应调制模块的b4和b6比特。两个编码器输出的编码序列同时进入交织器进行比特交织,交织方法如图7所示。交织器矩阵C是一个6×N的矩阵,编码器1输出的码字X1=(x11,x12,x31,…,x14N)按行写入矩阵的1、2、3、5行,编码器2输出的码字X2=(x21,x22,x23,…,x22N)写入第4行和第6行,然后按列读取输出交织器2,得到交织后的串行序列S=(s1,s2,s3,…,s6N)。
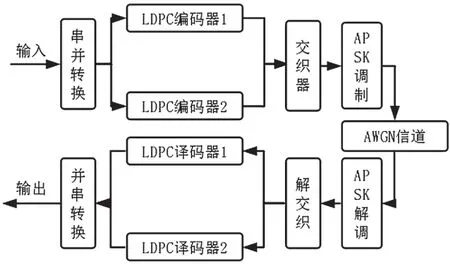
图6 基于64-APSK的非均衡LDPC编码设计系统
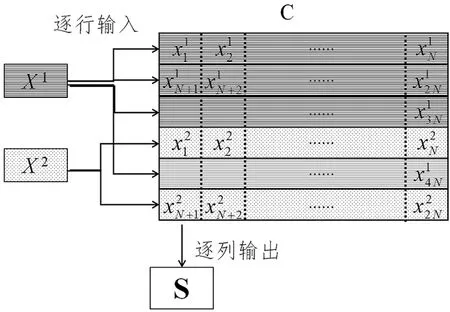
图7 交织器
该比特交织器的设计使得输出的串行码流可以直接进入APSK调制器进行调制,每6个比特映射成为一个星座点,直接保证了非均衡编码方案中不同LDPC编码与APSK调制中不同比特的对应性,同时使得信道上产生的差错随机化,更利于纠正突发性错误。
在接收端,对接收到的数据进行对应的APSK软解映射,得到各比特的LLR数据,然后解交织即根据图7所示交织器进行其逆操作,输出的两路LLR数据再输入两个对应的并行译码器进行译码,最终判决输出。由于LDPC译码模块不使用MSD而采用了并行设计,两个译码器同时进行译码处理,因此不会导致延时,提高了系统效率。
3 性能仿真与结果分析
利用MATLAB仿真软件,本文对提出的非均衡编码方案进行仿真和验证。在MLC方案中,为了选择合适的LDPC矩阵,会分析不同LDPC码的汉明距离,并以此匹配APSK中具有不同平均欧氏距离的比特。而本文对比特进行分组,因此在寻找对应的LDPC码时,通过改变LDPC的码率后仿真计算的方式进行搜索,从而确保所选的LDPC码既有较好的纠错能力,又不会带来大量的编码冗余。
本文提出的方案人为地将一组数据分割为经过不同编码器的两部分,误码性能较差的一部分数据将决定该方案的整体误码性能。非均衡方案的码率搭配必须合理,以保证两部分数据的性能非常接近。
本文采用LDPC编码器1和LDPC编码器2分别使用低压电力线通信标准中码率为0.6和0.3的LDPC码矩阵,0.6码率LDPC码码长为15 360, 0.3码率LDPC码码长为7 680,调制模块APSK星座图如图2所示。接收端LDPC译码器采用归一化min-sum迭代算法,对软信息进行修正的归一化因子α为0.8,最大迭代次数为50次。
在上述条件下,非均衡编码的两部分数据的不同误码性能,如图8所示。可以看到,在这样的分配情况下,b4b6部分的误码性能在误码率10-5时达到10.6 dB左右,代表了整体系统性能。此外,从图8也可以看出,b1b2b3b5与b4b6两部分误码性能非常接近,在误码率为10-4时仅有约0.06 dB的差异。因此,上述的搭配方案也较为合理。
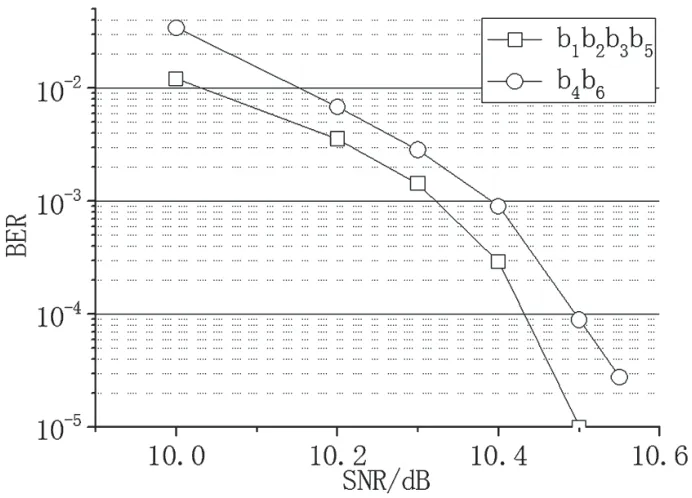
图8 非均衡编码方案中b1b2b3b5比特与b4b6比特的误码性能
为了验证非均衡编码方案的优越性,本文对传统编码调制系统进行了仿真。由于非均衡编码方案采用了0.3与0.6码率的LDPC码,综合码率为0.5,因此传统方案的仿真也采用码率相同的LDPC码以进行对比。调制方式、译码算法和最大迭代次数均与上述仿真参数相同,编码器采用低压电力线通信标准中码长为7 680、码率为0.5的LDPC码,误码性能如图9所示。可以看到,以性能较差的b4和b6比特的误码性能作为非均衡编码方案的整体性能,该方案性能优于电力线通信标准中0.5码率LDPC码方案约0.3 dB。因此,本文提出的方案在不增加编码冗余度的条件下,误码性能优于传统方案。
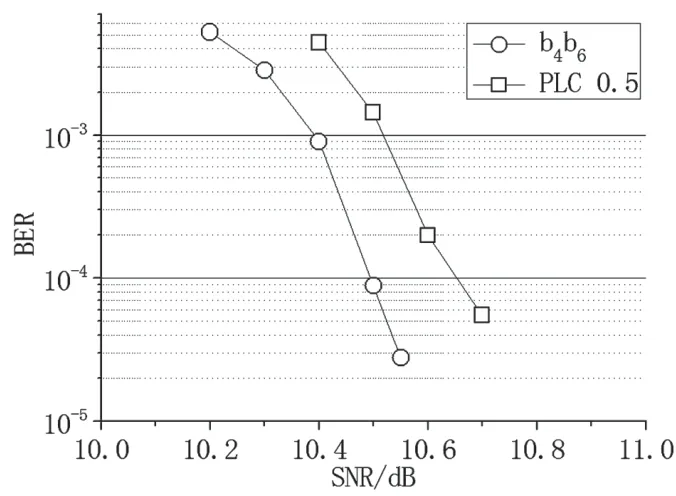
图9 非均衡编码中b4b6比特性能与传统方案性能对比
非均衡编码方案之所以优于传统方案,是因为对于APSK调制中差错保护较弱的部分数据,采用了具有更强纠错能力的LDPC码进行编码,改善了其误码性能,使其达到与保护较强数据相近的误码水平,进而提高其整体性能,解决了传统编码调制方案中低保护比特降低系统性能的问题。
4 结 语
本文分析了APSK的非均匀差错保护特性,创新性地提出了一种适用于64-APSK的非均衡LDPC编码方案,并通过MATLAB仿真软件进行了实验。结果表明,该方案在不增加编码冗余度的条件下依然具有较好的性能增益,同时由于进行了比特分组且采用了并行的编码和译码设计,改善了传统MLC方案的时延,进一步提高了系统效率。本文所述方案不仅适用于LDPC-APSK系统,对各种纠错编码级联高阶调制的编码调制系统均有参考意义,也为实际的硬件实现提供了理论参考。

