*不确定条件下提高静态电压稳定性的优化方法

邱一苇，林 今，吴 浩，宋永华，

(1.清华大学 电机工程与应用电子技术系，北京 100084；2.浙江大学 电气工程学院，杭州 310027；3.澳门大学 电子与计算机工程系，澳门 999078)

在当前电网大尺度跨区域互联，风、光等可再生能源发电跨越式发展，电力市场化改革不断深化的背景下，电力系统运行中的不确定性因素日益增多，其电压稳定性正受到全方位的考验[1-3]。为确保运行安全，有必要对电力系统在不确定性条件下的静态电压稳定性进行优化。

在不确定条件下的静态电压稳定性评估上，学界和业界已积累了许多积极的研究成果[4-10]。其中，静态安全域类评估方法通过离线计算获得参数空间中安全域边界的显式表示，在线运行时通过对比当前运行点与域边界的位置关系快速评估系统的静态电压稳定性，极大地提高了评估效率和灵活性[7-10]。但直接利用概率评估结果，提高不确定条件下电力系统静态电压稳定性的优化研究尚为有限。

为此，本文基于静态安全域思想提出了一种不确定条件下提高电力系统静态电压稳定性的优化方法：以最大化随机变量位于静态电压稳定域内的概率为目标，利用静态电压稳定域边界及控制变量对其灵敏度的显式逼近表达式构造优化模型；为此，引入广义多项式混沌(generalized polynomial chaos,gPC)思想，结合随机Galerkin方法和经典原-对偶内点法，求取静态电压稳定域边界及其灵敏度的显式多项式逼近表达式；最后，通过IEEE-39节点系统算例验证了所提方法的有效性和精确性。本文建模与计算工作在浙江大学智能电网运行与优化实验室开发的MASTES电力系统分析和仿真工具包[11]上进行。

1 不确定条件下的静态电压稳定优化模型

1.1 基于静态电压稳定域的优化模型

本文所提优化模型的目标在于，当电力系统中的随机变量服从一定随机分布时，通过调整运行点使系统静态电压失稳的概率最小化。

记多维独立随机变量构成向量：

Z=[Z1,Z2,…,Zn]∈Qn⊆Rn.

(1)

式中：Zi∈Qi为第i个独立随机变量；Qi为第i个独立随机变量的支持域；Qn=Q1⊗Q2⊗…⊗Qn为随机向量的支持域。对于含有非独立随机变量的情形，需进行预处理使之相互解耦，参见1.3节。

为刻画系统静态电压失稳的概率，引入静态电压稳定域[7]概念。计及发电机无功出力约束时，电力系统的稳态模型[13]如下所示：

0=f(V,θ,Ps,QG;λ,Z) .

(2)

(3)

(4)

(5)

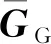
基于上述模型，定义概率空间中的静态电压稳定域，如下：

ΩSVSR={Z∈Qn⊆Rn|系统(2)-
(5)运行点存在} .

(6)

显然，当随机变量位于域内时，系统静态电压稳定；反之意味着失稳。因此，系统静态电压稳定的概率即随机变量位于静态电压稳定域中的概率：

(7)

式中：dW(Z)=dW1(Z1)dW2(Z2)…dWn(Zn)为多维概率空间的测度；dWi(Zi)=ωi(Zi)dZi为第i个独立随机变量所在概率空间的测度；ωi(Zi)为第i个独立随机变量的概率密度函数；且

(8)

至此，以最大化多维随机变量处于静态电压稳定域内的概率为主要目标，兼顾控制变量的调整幅度，定义不确定条件下提高静态电压稳定性的优化模型，如下：

min-ΔP(Z∈ΩSVSR)+(ΔU)TR(ΔU) ,

(9)

(10)

(11)

式中：U为控制变量，通常包括发电机电压整定值、无功补偿装置的安装/投入量等；ΔU为控制变量的增量；R为权重系数矩阵。注意到因引入了静态安全域，上述优化模型中无需包含显式的原始系统模型式(2)-(5)，故求解计算量极小。

需要指出，亦可将节点电压安全约束、线路热稳定约束等其他类型的安全约束加入模型式(2)-(5)中，将本文方法和结论拓展至更为综合的静态安全上。

1.2 优化模型化简

目标函数式(9)中概率项ΔP(Z∈ΩSVSR)无显式解析表达式，故优化模型难以直接求解。为此，引入静态电压稳定域边界的显式近似，形式如下[9]：

(12)

(13)

依据式(7)，将调整控制变量后系统静态电压稳定的概率增量写成条件概率的形式：

(14)

考虑到控制变量U的调整量通常较小，其调整范围内Z1的概率密度ω1(Z1)变化亦较小，故式中：

(15)

将式(15)代入式(14)中，则调整控制变量后随机变量位于稳定域中概率的近似增量可由下式给出：

ΔP(Z∈ΩSVSR)≈ΔP*(Z∈ΩSVSR)=

(16)

图1 调整控制变量后随机向量位于稳定域内概率的示意图Fig.1 Probability of the random vector staying within the stability region after adjusting control variables

将目标函数式(9)中的概率项替换为近似表达式(16)，则优化模型式(9)-(11)成为一组确定性优化问题，可由经典非线性规划方法直接求解。

1.3 随机变量相关性的预处理

风、光等可再生能源的出力存在一定相关性；不同节点负荷相互之间亦可能具有相关性。如前所述，本文所提方法要求各随机变量间相互独立，故需事先对非独立随机变量进行解耦，具体实现方法可参考文献[14].

随机变量维数较高时，为降低计算量，亦可参考文献[15]对随机变量进行降维处理。由于随机变量的解耦和降维并非本文关注重点，故不再赘述。

2 静态电压稳定域边界的多项式逼近

为便于处理随机变量波动范围较大时发电机无功越限组合的切换，并在计算稳定域边界近似表达式的同时得到控制变量对其灵敏度，本节引入一种基于随机Galerkin方法的参数化非线性规划问题多项式逼近方法。

2.1 静态电压稳定域边界的参数化非线性规划模型表示

由静态电压稳定极限的定义[14]，将概率空间中的静态电压稳定域边界由如下参数化非线性规划模型表示[10]：

(17)

(18)

(19)

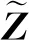
2.2 参数化非线性规划模型的参数化KKT条件

利用经典原-对偶内点法(primal-dual interior point method,PDIPM)思想将参数化非线性规划模型式(17)-(19)转换为参数化非线性代数方程模型。首先，为不等式约束式(19)引入松弛变量：

(20)

使

(21)

并引入对数障碍函数，构造参数化Lagrange函数：

(22)

令参数化Lagrange函数式(22)对各原/对偶变量的偏导为0，可得参数化KKT条件：

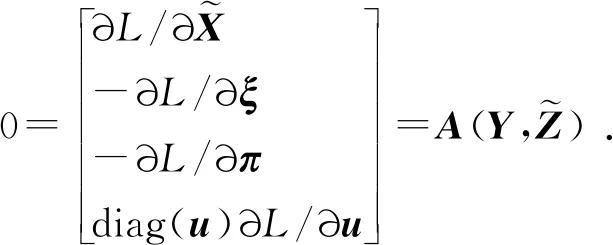
(23)

式中：Y=[XT,uT,ξT,πT]T为所有原、对偶变量构成的向量。

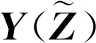
2.3 广义多项式混沌展开式

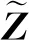
(24)

并取如下张量积作为完整的多项式基函数集：

(25)

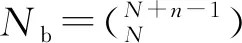
若随机变量不服从表1给出的任意1种分布类型，则依据等概率原则将其变换至其中任意1种分布类型，继而进行后续的逼近计算。

表1 随机分布对应的Wiener-Askey混沌多项式基函数Table 1 Wiener-Askey chaos polynomial basis corresponding to the types of random variables

以式(25)中多项式基函数的线性组合构造Y的gPC展开式，如下：

(26)

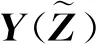
2.4 随机Galerkin方法

采用随机Galerkin方法构造投影方程以求解gPC展开式(26)中的待定系数。首先定义期望泛函：

(27)

并基于此定义Hilbert空间

U={h(·)|h:Rn-1→R,〈·,·〉} .

(28)

其上2个元素的内积定义为其乘积的期望：

(29)

将Y中各变量的gPC展开式(26)代入参数化KKT条件式(23)中，并将其向(25)中各个基函数以内积形式(29)作投影以消去随机变量，形成以展开系数为待定变量的确定性Galerkin投影方程组：

(30)

3 算例分析

采用如图2所示IEEE-39节点系统进行算例分析，计及所有10台发电机的无功出力约束。恒功率因数增长模式下，初始负荷裕度为51.7%.

图2 IEEE-39节点系统接线图Fig.2 Topology diagram of IEEE 39-bus system

令优化前系统整体负荷增长因子λ为40%.在此基础上，取区域{13,15,16,17,20,21,23,34}和{25,26,27,28,29}的负荷增长因子作为随机变量，记为λ1和λ2，并假设λ1服从μ=0,σ=0.1的高斯分布，λ2服从a=2,b=4的Beta分布。采用Monte Carlo模拟验证准确性时，采样数NMC取100 000.

3.1 静态电压稳定域边界的逼近结果

首先应用第2节所述方法求取系统静态电压稳定域边界及控制变量对其灵敏度的显式近似表达式。取gPC展开阶数N=5，图3给出了{λ1,λ2}空间中静态电压稳定域边界的逼近，及其上各点的失稳机理。其中，SNB{30,31,35,37,38}表示发电机{30, 31,35, 37, 38}处于无功越限状态时发生的鞍结分岔；LIB36-{30,31,35,37,38}则表示发电机{30,31,35,37,38}已处于无功越限状态时，发电机36无功越限引发的极限诱导分岔。域边界逼近结果的表达式如下：

(31)

由图3可知，尽管随机变量变化时系统的静态电压失稳机理发生了多次切换，逼近结果仍很好地贴合了实际边界。将逼近表达式(29)代入式(7)中，得优化前系统静态电压失稳的概率为5.364%，这与Monte Carlo模拟所得结果5.391%相比非常接近，故从另一方面验证了逼近结果的准确性。这为后续优化提供了坚实的基础。

图3 优化前系统静态电压稳定域边界及其逼近Fig.3 Static voltage stability region boundary before optimization and its approximation

3.2 不确定条件下静态电压稳定性的优化

取所有10台发电机的电压设定值作为控制变量，其上下限分别设置为0.92和1.08，相较于初始值上下调整幅度限制设置为0.05，目标函数(9)中系数矩阵R=diag([0.1],…,[0,1]T)，进行优化。

优化模型给出的目标函数中，失稳概率降低至2.054%.根据优化结果调整控制变量，以Monte Carlo 模拟计算失稳概率，结果为2.215%，二者基本一致。优化前后系统的静态电压稳定域边界如图4所示。图中亦给出了随机变量的采样点。显然，优化结果将静态电压稳定域大幅向外拓展，使更多随机采样落在了稳定域的内部，故由此大幅降低了系统静态电压失稳的概率。

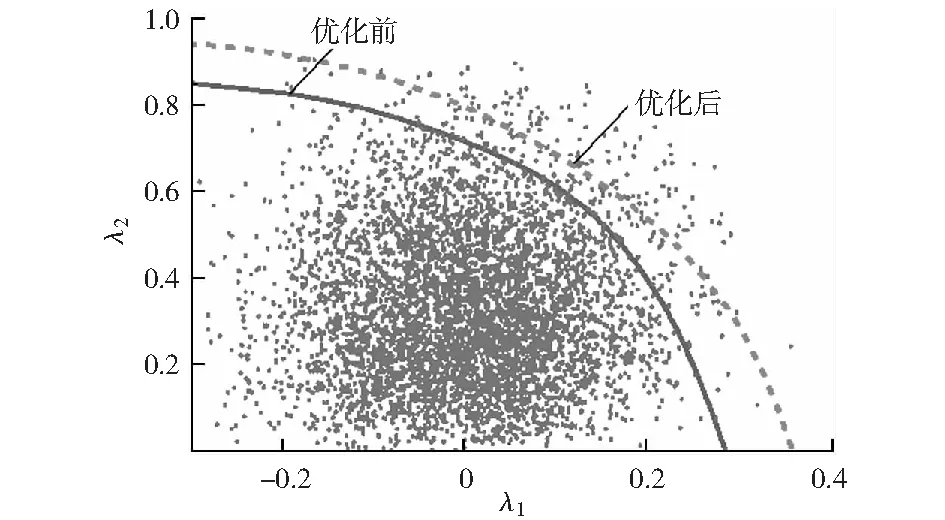
图4 优化前后静态电压稳定域边界对比Fig.4 Comparison between the static voltage stability region boundaries before and after optimization

优化前后的控制变量，即各发电机节点电压幅值的设定值则由图5给出。由图可知，优化结果提高了32,33,34,36,37,38等6台发电机的电压幅值设定值。其中发电机36在优化后达到了1.08的上

限，其余5台发电机电压设定值的增量则达到0.05的上限。另有4台发电机的电压设定值因其对优化目标的灵敏度为0，故优化结果未对其作任何调整，这表明并非简单提高发电机电压设定值即可提高系统的电压稳定性。

图5 优化前后发电机节点电压幅值的设定值Fig.5 Generator voltage magnitude setting values before and after optimization

最后，讨论控制变量调整量的权重系数R对优化结果的影响。逐次提高控制量调整量在目标函数中的权重，并采用Monte Carlo模拟求取优化后系统的失稳概率，结果由表2给出。可以看出随着控制量权重的增加，优化后系统的失稳概率也随之增加。考虑到增大权重系数可以避免发电机设定电压的调整幅度过大，权重系数取1左右为佳。

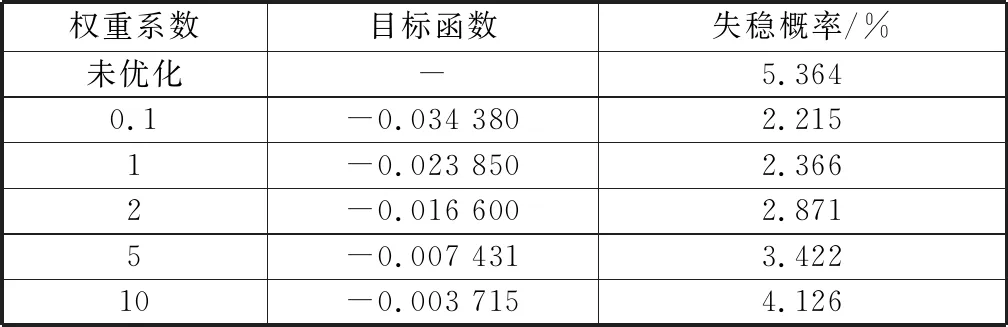
表2 控制变量调整权重对优化目标的影响Table 2 Impact of weight of change in control variables on the optimization objective

4 结论

本文提出了一种基于域的不确定条件下降低电力系统静态电压失稳概率的优化方法。结果表明所提方法能够有效扩展概率空间中的静态电压稳定域，从而提升系统的静态电压稳定性。

本文以最小化失稳概率作为优化目标，建模仍较为简单，尚未考虑其与传统无功优化目标之间的协调。将经济性因素考虑在内形成综合的风险-效益指标，提出更为全面的优化模型和方法将是下一步的研究内容。