月相和温度对棉红铃虫成虫种群动态的影响

余 纯，许 冬，黄 维，雷明洪，万 鹏，*

(1.江西财经大学 统计学院，江西 南昌 330013； 2.农业农村部华中作物有害生物综合治理重点实验室/农作物病虫草害防控湖北省重点实验室/湖北省农业科学院植保土肥研究所，湖北 武汉 430064； 3.湖南省安乡县植保植检站，湖南 安乡 415600)

昆虫的发生与生理行为受环境影响，不同种类的昆虫，对外界环境条件中的温度、湿度、光照甚至月相等因子的适应性各不相同。如枣镰翅小卷蛾(Ancylissativa)和二化螟(Chilosuppressalis)在高温时求偶持续时间缩短[1]，异色瓢虫在低温下的飞行能力较强但搜索能力较弱[2]，棉铃虫(Helicoverpazea)雌成虫在高温或低温条件下性信息素释放量均会减少[3]。甜菜夜蛾成虫寿命随湿度的提高而增加[4]，湿地松粉蚧若虫的存活率随降雨强度的增加显著下降[5]。长光照能促进异色瓢虫的求偶交配欲[6]，短日照能减少稻纵卷叶螟的南迁[7]，三化螟在满月期的扑灯数显著少于月亏期，而黑尾叶蝉的诱集量在满月期显著高于其他月相期[8]。因此，研究环境因子对各种昆虫生理行为的影响，有助于深入认识该昆虫与环境之间的互作规律，为其在生产上的治理提供理论依据。

红铃虫为长江流域棉花上的重要害虫，能严重危害棉花的产量与品质。有研究表明，月相和温度均能显著影响红铃虫的发生[9]。为此，本研究采用性信息素诱集的方式，监测了湖南安乡棉区的红铃虫种群动态，并运用非凸惩罚的稳健线性回归模型，分析了月相与温度对红铃虫发生量的影响，以期能加深对红铃虫发生规律的认识，为该地区红铃虫的综合治理提供理论依据。

1 材料与方法

1.1 基于性诱剂的红铃虫种群动态监测

2012—2015年，在红铃虫的盛发期，采用红铃虫信息素诱集器(北京中捷四方生物科技股份有限公司)在湖南省安乡县的棉田内进行红铃虫成虫诱集。按照说明书组装好诱集器各组件，将其放置于棉田内，使诱集器高于棉花植株0.5 m，每天收集所诱成虫并记数。为保证诱集效果，每月更换1次诱芯。诱集时间从每年的5月下旬至9月底。

1.2 红铃虫监测点气象数据的获取

红铃虫监测点的气象数据从安乡县气象局获取。

1.3 数据处理与分析

本研究采用稳健的回归分析——基于非凸惩罚的线性回归模型，研究红铃虫种群与月相、温度之间的关系，以避免观察数据中极端值或离群值对模型参数估计的影响。在回归分析前，从3个方面进行考虑：一是完全用阴历的日期来代替月相，分析不同月相时红铃虫的发生量；二是根据月相，将阴历的日期拆分成新月、弦月、满月等时间段，分别赋值，分析其与红铃虫发生量之间的关系；第三是除月相外，还需考虑光线的影响，即夜间光线的强弱并结合月相来对阴历的每天进行赋值，再由此分析其与红铃虫发生量之间的关系。具体赋值情况如下：雨天，0；阴天，1；多云，2；晴天则依月相的不同而赋值不同，其中新月、残月(农历初1、初2、29、30)，3；蛾眉月(农历初3、初4、27、28)，4；蛾眉月(农历初5、初6、25、26)，5；弦月(农历初7、初8、23、24)，6；弦月(农历初9、初10、21、22)，7；凸月(农历11、12、19、20)，8；凸月(农历13、14、17、18)，9；满月(农历15、16)，10。

1.3.1 线性回归模型

对于给定的相互独立的、具同样分布特征(independent and identically distributed， iid)的观测值(xi，yi)，i=1，2，3，…，n。为了研究因变量(y)和自变量(x)之间的关系，通常用以下的线性回归模型：

y=Xβ+，～N(0，σ2I)。

(1)

模型中y=(y1，…，yn)T，是n个观测值yi组成的向量，如果有p(p≥ 1)个自变量，X就是维度为n×(p+1)的矩阵。β=(β0，β1，…，βp)T是维度为(p+1)×1的未知系数向量。=(1，…，n)T是随机的误差向量，假定其服从多元正态分布时，对于第i个观测值(xi，yi)，yi和xi满足如下关系：i。最常用的估计系数向量β的方法是最小二乘法，其工作原理就是使得残差平方和最小。

Yu等[10]指出，当数据中出现极端值或离群值时，最小二乘法不能准确估计系数向量β。在此情况下，需要运用稳健的线性回归模型来处理数据并检测离群值。

1.3.2 基于非凸惩罚的稳健线性回归模型

She等[11]提出了基于非凸惩罚的稳健线性回归模型：

y=Xβ+γ+，～N(0，σ2I)。

(2)

这个稳健的线性回归模型(2)是在传统的线性回归模型(1)中引入一个均值漂移参数γ=(γ1，…，γn)T，n是样本容量。当第i个观测值为离群值时，γi值为非零；否则，γi为0。模型(2)通过对均值漂移参数γ的准确估计，可达到同时估计参数β和检测离群值的目的。可通过使如下的目标函数达到最小来估计参数β和γ。

(3)

式(3)中，pλ(|γi|)是关于γi的惩罚函数，λ是调谐参数。

1.3.3 惩罚函数与阈值法则

上文所述目标函数(3)中的惩罚函数可以有多种选择，比较普遍的有l0范数和l1范数，以及SCAD等惩罚函数[12-15]。每个惩罚函数都有其对应的阈值法则(thresholding rule)，比如l0范数的惩罚函数对应有hard阈值法则，l1范数的惩罚函数对应于soft阈值法则，SCAD的惩罚函数对应于SCAD阈值法则。本研究中我们采用l0范数的惩罚函数：

式中，I(·)为指示函数(indicator function)。l0范数的惩罚函数对应于以下的hard阈值法则：

(4)

式(4)中，Θ为阈值法则函数，ξ为变量，λ为调谐参数。

1.3.4 参数估计的具体算法

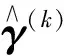
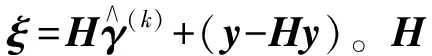
1.3.5 调谐参数λ最优取值的选择

因为惩罚函数和阈值法则中包含调谐参数λ，很显然λ控制γi的估计值，所以调谐参数λ的取值对准确估计γi起到很重要的作用。经验的做法是在(λmin，λmax)范围内取100个λ值，其中，λmin是λ的最小取值，使得向量γ=(γ1，…，γn)T中50%的γi值非零，λmax对应的是λ的最大取值，使得向量γ中所有的γi为0。显然100个不同的λ值对应100组不同的向量γ=(γ1，…，γn)T的估计值，我们用BIC(bayesian information criterion)的标准来选择最优的调谐参数λ取值。选定最优的调谐参数λ取值后，其对应的一组γ估计值即为最终的参数γ估计值。

通过对参数γ和β的准确估计，稳健线性回归模型(2)可以实现同时进行离群值检测和模型参数估计。

2 结果与分析

2.1 月相对诱蛾量的影响

以月相作为自变量(X)，诱蛾量作为因变量(Y)，分别对2012年、2013年、2014年和2015年的数据做诱蛾量与月相之间的线性回归分析。同时，为了增加数据的代表性，增大样本容量，2012—2015年的数据也被合并进行了线性回归分析，以期拟合出更准确的回归模型。考虑到诱蛾量的观测值在(0，1 100)之间，变量取值的范围和方差太大会给线性回归的参数估计带来较大的误差，故在数据分析时以诱蛾量除以10作为因变量Y的取值。如上文所述，我们建立稳健的线性回归模型为：Y=β0+β1X+γ+。模型中β0、β1和γ为3个未知的参数，其中β0为截距，即当月相取值为0(下雨天气)时的平均灯诱蛾量；β1为斜率，即当月相每增加1个单位时，平均诱蛾量的变化。均值漂移参数γ=(γ1，…，γn)T是离群值指示器。如果估计的γi为非零，则第i个观测值是离群值。除了参数估计，本研究还进行了模型显著性t检验，用于检验的2个假设分别为零假设H0:β1=0和备择假设Ha:β1≠0。

图1展示了2012年、2013年、2014年和2015年和2012—2015年汇总数据中诱蛾量与月相之间关系的散点图。为了使散点图更直观地呈现模型的特征，各散点图中添加了线性回归趋势线。图1显示诱蛾量与月相存在负相关关系，这一共性在各年份和汇总数据中都有明显的体现。各年份的数据和2012—2015年汇总数据中都存在离群值，检测出的离群值用星号标记。而且，模型拟合出的回归趋势线并没受离群值的影响，体现出所用线性回归模型的稳健性。

表1显示了对于诱蛾量(Y)与月相(X)的稳健线性回归模型中非零的γ估计值。从中可以看出：2012年的数据中，第100、101、104、105和114个观测值为离群值。2013年的数据中，第43和45个观测值为离群值。2014年的数据中，第1、100和101个观测值为离群值。2015年的数据中，第6个观测值为离群值。2012—2015年的汇总数据中，第100和320个观测值为离群值。其他的γ估计值为0，说明其对应的观测值为正常值。

表2为诱蛾量(Y)与月相(X)的稳健线性回归分析的参数估计和假设检验结果。从表中可以看出，在模型显著性检验中，各年份诱蛾量与月相的线性回归模型都在5%显著性水平下表现显著。在各年份的数据和汇总数据中诱蛾量(Y)与月相(X)之间的线性回归方程非常接近。而且，由各年份的数据和汇总数据得出的95%置信区间相互重叠，说明诱蛾量(Y)与月相(X)之间的线性关系在不同的年份表现出相同的模式，且月相对诱蛾量的抑制程度在不同的年份没有表现出显著区别。以2012—2015年的汇总数据为例，晚上没有月亮时，平均诱蛾量为169头。月相在0～10的取值范围内，月相每增加1个单位，平均诱蛾量下降11头。

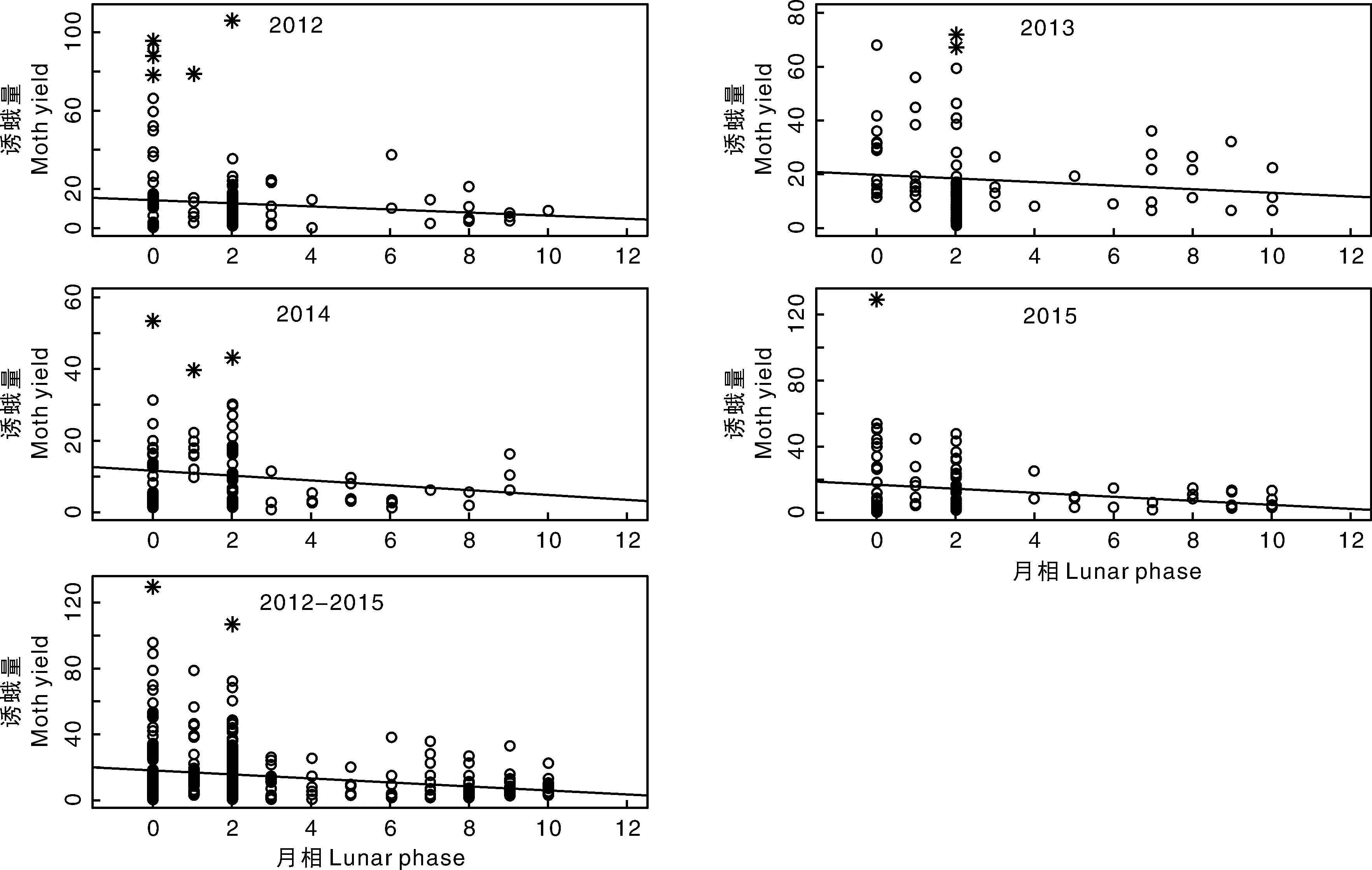
图中星号代表离群值。下同。The asterisks (*) represent the outliers. The same as bellow.图1 2012、2013、2014、2015年和2012—2015年汇总数据中诱蛾量与月相之间关系的散点图Fig.1 Scatter plots of moth yield and lunar phase in year 2012， 2013， 2014， 2015 and 2012-2015 combined data

表1诱蛾量与月相的稳健线性回归模型参数γ的估计

Table1Estimation of parameterγof robust linear regression model with moth yield and lunar phase

年份Year样本容量Sample size离群值数Number of outliers非零的γ估计值Estimated nonzero γ20121165γ100=90.47,γ101=68.63,γ104=58.73,γ105=58.93,γ114=75.932013832γ43=51.31,γ45=47.5720141153γ1=40.32,γ100=28.39,γ101=30.0220151221γ6=112.022012—20154362γ100=91.46,γ320=111.69

表2诱蛾量与月相的稳健线性回归分析结果

Table2Results of robust linear regression analysis for the model with moth yield and lunar phase

年份Year数据量Sample size估计的回归方程Estimated regression equationβ的95%置信区间95% confidence intervalt检验P值P value of t test20122013201420152012-201511683115120436Y=19.107-1.888XY=23.364-1.500XY=13.280-1.083XY=15.639-1.079XY=16.900-1.178X(-3.294,-0.481)(-2.581,-0.418)(-1.844,-0.323)(-2.077,-0.081)(-1.722,-0.634)0.0090.0070.0060.034<0.001

2.2 温度对诱蛾量的影响

把日平均温度作为自变量(X)，诱蛾量作为因变量(Y)，分别对2012年、2013年、2014年和2015年的数据以及2012—2015年汇总数据做诱蛾量与日平均温度之间的稳健线性回归分析。这部分所建立的线性回归模型、参数含义和模型显著性检验和2.1节所述一样。

图2报告了各年份和2012—2015年汇总数据中诱蛾量与日平均温度的散点图。和图1展示的一样，在各图中加入线性回归趋势线。图2显示诱蛾量与温度存在负相关的关系，这一共性在各年份和汇总数据中都有明显的体现。各年份的数据和2012—2015年汇总数据中都存在离群值，检测出的离群值用星号标记。而且，和前文所述一样，模型拟合出的回归直线并没有受离群值的影响，体现出所用的线性回归模型的稳健性。

图2 2012、2013、2014、2015年和2012—2015年汇总数据诱蛾量与日平均温度的散点图Fig.2 Scatter plots of moth yield and daily mean temperature in year 2012， 2013， 2014， 2015 and 2012-2015 combined data

表3报告了对于诱蛾量(Y)与温度(X)的稳健线性回归模型中非零的γ估计值。从表3可以看出：2012年的数据中，第100、101、104、105和114个观测值为离群值；2013年的数据中，第43、45、53、54和55个观测值为离群值；2014年的数据中，第1、99和100个观测值为离群值；2015年的数据中，第6个观测值为离群值；2012—2015年的汇总数据中，第100和320个观测值为离群值。

表4报告了对于诱蛾量(Y)与温度(X)的稳健线性回归分析结果。从表4可以看出，各年份和汇总数据拟合的模型在5%显著性水平下都表现为显著。在各年份数据中诱蛾量(Y)与温度(X)之间的线性回归方程非常接近。而且，由各年份数据和汇总数据得出的β1的95%置信区间相互重叠，说明诱蛾量(Y)与温度(X)之间的线性关系在不同年份表现出相同的模式，且温度对诱蛾量的抑制程度在不同年份没有表现出显著区别。以2012—2015年的汇总数据为例，当日平均温度为15～35 ℃时，温度每增加1 ℃，平均诱蛾量减少10头。

2.3 月相和温度对诱蛾量的影响

在分析诱蛾量与单个因素(月相或温度)之间关系的基础上，我们还考虑在诱蛾量(Y)与月相(X1)之间的线性回归模型中加入第2个变量——温度(X2)。得到如下稳健二元线性回归模型：Y=β0+β1X1+β2X2+γ+。在对二元线性回归模型进行显著性假设检验中，月相(X1)在2012、2013、2014和2015年均表现为不显著；月相和温度在2012—2015年汇总数据中均表现为显著。所以，我们只在2012—2015年汇总数据中同时考虑诱蛾量(Y)与月相(X1)和温度(X2)以建立线性回归模型。

图3展示了2012—2015年的汇总数据中诱蛾量(Y)与月相(X1)和日平均温度(X2)三维散点图，在图中2个离群值用星号标注出来。从图中的长方形趋势平面来看，月相和温度都与诱蛾量呈负相关，说明月相和温度都对诱蛾量有抑制作用。对2012—2015年的汇总数据中诱蛾量(Y)与月相(X1)和日平均温度(X2)建立稳健的线性回归模型进行参数估计，非零的估计为：γ100=92.90，γ320=113.49，显示第100和320个观测值为离群值。在对模型的显著性检验中，二元线性回归模型在5%显著性水平下表现显著(F检验的P值为2.957e-07<0.05)。而且月相(X1)和温度(X2)2个变量在单独显著性检验中都表现为显著(对X1和X2的t检验P值分别为0.020 2和0.000 1)。估计出的线性回归模型方程为Y=39.066 - 0.680X1-0.842X2。当温度保持恒定时，月相每增加1个单位，平均诱蛾量减少7头；当月相保持恒定时，日平均温度每增加1 ℃，平均诱蛾量减少8头。

表3诱蛾量与温度的稳健线性回归模型参数γ的估计

Table3Estimation of parameterγof robust linear regression model with moth yield and temperature

年份Year数据量Sample size离群值数Number of outliers非零的γ估计值Estimated nonzero γ20122013201420152012—20151168311512243655312γ100=94.65, γ101=74.14, γ104=59.22, γ105=55.24, γ114=71γ43=57.37, γ45=53.12, γ53=38.48, γ54=41.09, γ55=48.84 γ1=42.83, γ99=29.82, γ100=29.99γ6=116.78γ100=93.28, γ320=115.05

表4诱蛾量与温度的稳健线性回归分析结果

Table4Results of robust linear regression analysis for the model with moth yield and temperature

年份Year样本容量Sample size估计的回归方程Estimated regression equationβ的95%置信区间95% confidence intervalt检验P值P value of t test20122013201420152012—201511683115122436Y=59.645-1.674XY=36.644-0.6973XY=29.627-0.725XY=40.234-1.004XY=42.484-1.023X(-2.403,-0.944)(-1.208,-0.186)(-1.188,-0.263)(-1.879,-0.129)(-1.422,-0.625)0.00010.00810.00240.0249<0.0001

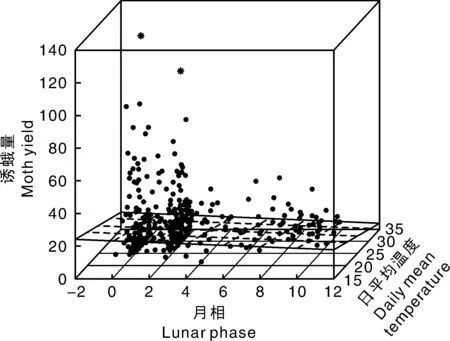
图3 2012—2015年汇总数据诱蛾量与月相和日平均温度的三维散点图Fig.3 Three dimensional scatter plot of moth yield and lunar phase and daily mean temperature for 2012-2015 combined data

3 结论与讨论

盛承发等[9]通过圆形分析表明：从全月来看，红铃虫性诱剂诱蛾高峰集中角无统计意义；从分上、下半月来看，红铃虫的性诱蛾高峰数与月相有一定关系，即望、朔蛾峰均少，上弦(初7、初8)、下弦(22～23日)蛾峰均较多。但他仅分析了红铃虫的蛾峰与月相的关系。本研究将红铃虫全年的发生动态与月相之间的关系进行了分析，研究表明，红铃虫发生量在全年内与月相无显著相关性，但进一步将天气因素考虑进去后发现，夜间光线对红铃虫发生量的影响更大，即夜间光线越强，红铃虫的诱蛾量就越小，反之则大。该结果表明，月相对红铃虫成虫活动的影响主要由夜间光线引起，月相本身(月球引力)并不影响红铃虫的发生。

与光线相比较，温度对昆虫发生的影响更大。一般而言，影响昆虫生长发育的是有效积温。在其发育起点温度之上时，随温度的上升，昆虫生长发育速率加快，导致昆虫的种群数量也随之上升，但温度过高也会增加其死亡率。在田间条件下，红铃虫的盛发期为每年的6月中下旬至10月上旬，在此期间，如果天气呈现出高温高湿条件，就会促进红铃虫的发生，从而导致其发生量大，为害加重。但从本研究结果来看，温度为15～35 ℃时，随温度的上升，红铃虫成虫的活动显著下降，即较高的温度对红铃虫成虫活动有抑制作用。由于温度能影响棉铃虫的性信息素分泌，如在22～30 ℃条件下，温度越低，棉铃虫性信息素的分泌量越多[16]。因此，在本研究中，高温对红铃虫诱蛾量的抑制可能与红铃虫的性信息素分泌有关。

线性回归模型是研究因变量与2个甚至几个变量(因子)之间关系的主要统计分析方法，通常采用最小二乘法来估计回归模型中的参数。但是最小二乘法对离群值很敏感，从而影响数据分析的结果。本研究采用了基于非凸惩罚的线性回归模型来进行分析，该方法具备同时进行离群值检测和稳健参数估计的功能。分析结果表明，2012—2015年红铃虫的诱蛾量均存在离群值，显示其不适合用最小二乘法分析。但在处理离群值时，本研究并没有全部舍弃，而是根据实际情况进行了分析，比如在2012年的数据中，分析出有离群值5个，分别为第100、101、104、105和114。本研究仅舍弃了第100个数据，即9月7日的诱蛾量。原因是：第一，该数值在本年中最高，显示其为蛾峰值；第二，其实际值与预测值之间的残差最大。表明这一天的诱蛾量主要受红铃虫成虫发生高峰的影响，故本研究舍弃了该值。其他几个离群值虽然实际值与预测值的残差较大，但它们低于蛾峰值，且其与前后几天的诱蛾量差异比较小，表明其主要受环境影响所致，故加以保留。同理，对2013年的数据仅舍弃了第43个，2014年的数据没有舍弃，2015年的数据舍弃了第6个。这些值都为当年的蛾峰值。经此处理后，各年份的回归模型t测验的P值均有显著提升，进一步证明了文中对离群值处理的合理性。同理，在处理温度与诱蛾量回归的离群值时，也仅舍弃了蛾高峰期的数据，其他均予以保留。

红铃虫发生除受月相影响外，受降雨的影响也较大。在一定条件下，红铃虫成虫的活动与雨量呈正相关，即在较小雨量下，弱光和高湿有利于红铃虫成虫的活动与产卵；但当雨量过大时，红铃虫成虫的活动受到抑制[17]。说明红铃虫的发生非常复杂，是多种因素共同作用的结果。如能更系统地研究这些因子对红铃虫发生与行为的影响，将有助于深化对红铃虫发生规律的认识，从而在生产上制定合适的防治对策。