基于犹豫直觉模糊语言集均值-标准差偏好距离的多属性决策研究
刘东海,刘原园,陈晓红
(1.湖南科技大学应用统计系,湖南 湘潭 411201;2.湖南商学院 湖南省移动电子商务协同创新中心,湖南 长沙 410205)
1 引言
1965年,Zadeh[1]在X={x1,x2,…,xn}上定义了模糊集A={(xi,μA(xi))xi∈X},其中μA(xi)∈[0,1]表示xi∈X的隶属度。Atanassov[2]认为模糊集只考虑了xi∈X的隶属度并没有考虑其非隶属度,为了更好地对相关信息进行描述,提出了直觉模糊集A′={xi,(μA′(xi),νA′(xi),πA′(xi))xi∈X},且μA′(xi)+νA′(xi)+πA′(xi)=1,其中μA′(xi),νA′(xi),πA′(xi)∈[0,1]分别表示xi∈X的隶属度,非隶属度和犹豫度。人们常用直觉模糊集来描述和处理多属性群决策问题中的不确定信息,如Liang等[3]针对混合型的不完全评价信息,提出了一种基于直觉模糊集和证据理论的决策方法,解决了供应商选择的多属性决策问题,Yue[4]将直觉模糊集理论应用到双边匹配决策领域中,给出了一种直觉模糊集信息下双边匹配的决策途径。直觉模糊集中隶属度和非隶属度是用确定的数值表示,在一些决策问题中,由于决策环境的复杂性、不确定性以及决策者对评价对象的主观认识,此时人们无法用精确的数值来对他们进行评价。例如,评价某一公司投资方案的优劣时,决策者可能会说“这个投资方案整体上是好的,但可行性有一点弱”等语言术语,语言术语表达的观点与人们的认知非常接近,但其运算有点复杂。Zadeh[5-7]定义了语言集S,用语言术语表达决策信息,如七值语言集S可表示为S={s0:非常低,s1:很低,s2:低,s3:中等,s4:高,s5:很高,s6:非常高}。一些学者利用语言集表达信息的可行性和灵活性来考虑多属性群决策问题,如Herrera等[8]考虑了语言评估的一致性,进一步Herrera等[9]利用语言有序加权算子研究了个体语言偏好关系的群决策问题,Xu Zeshui[10]提出了利用语言混合聚合算子解决具有不确定乘性语言偏好关系的群决策问题。但在一些实际问题的评价中,如专家组对某地区的洪涝灾害风险进行评估时,决策者认为该地区的风险“有可能是中等,有可能是高”,此时无法用单一的语言术语来表达他们的评价信息[11]。为此,Liao Huchang等[13]提出了犹豫模糊语言集HS={(xi,MS(xi)xi∈X)},其中MS(xi)是由多个语言术语构成的集合,如MS(xi)={s3,s4}表示xi∈X隶属度有可能是中等,有可能是高。犹豫模糊语言集虽能灵活地反映决策者的犹豫程度,但它没有表示xi∈X语言评价术语的非隶属度,并没有全面反映决策者对评价对象的评价情况。为此,Beg和Rashid[14]提出了犹豫直觉模糊语言集ES={(xi,MS(xi),NS(xi))xi∈X},其中MS(xi),NS(xi)是语言集的子集,分别表示xi∈X语言评价术语的隶属度和非隶属度。
另一方面,基于距离测度的决策方法是多属性决策问题中一种重要的决策方法,它是描述评价集合之间不同性的一种度量。一些学者对语言集、犹豫模糊语言集、犹豫直觉模糊语言集的距离进行了研究,并将它们广泛应用到数据挖掘、模式识别等领域。Xu Zeshui[15]定义了语言术语的偏离度,并将其应用于语言偏好关系的群决策问题,但此距离仅适合两个语言集语言术语个数相同的情况。Liao Huchang等[16]在Xu Zeshui[15]的基础上考虑了当两个犹豫模糊语言集语言术语个数不相同时,根据决策者的风险偏好将两个犹豫模糊语言集的语言术语个数添加至相同,并定义了犹豫模糊语言集的混合Hamming距离和混合Euclidean距离,提出了基于相应距离测度的决策方案排序问题。进一步Beg和Rashid[14]提出了犹豫直觉模糊语言集的包络距离,在这个距离测度中,只用了语言术语隶属度与非隶属度的最大值和最小值,并没有考虑其余的语言术语评价值,这就有可能出现评价信息失真的情况。在文献[14-16]中定义的语言集距离均是用语言变量的下标值计算,这失去了语言术语集本身表达的优势,且没有体现在不同语义环境下语言术语评价值的差别。基于上述研究,本文将运用语言尺度函数,定义基于犹豫直觉模糊语言集均值-标准差偏好的Hamming距离,提出基于犹豫直觉模糊语言集距离测度的TOPSIS和TODIM的多属性群决策方法,并利用这两种方法对评估对象进行排序。
本文的结构是:第二节给出了预备知识;第三节定义了基于犹豫直觉模糊语言集均值-标准差的距离测度,并证明了它的相关性质;第四节给出了基于犹豫直觉模糊语言集均值-标准差距离的TOPSIS和TODIM决策方法;第五节通过实例验证了上述方法的可行性和有效性,并与已有方法进行了比较;第六节对全文进行了总结,并对将要进行的研究做了展望。
2 预备知识
2.1 语言集
定义1[5]设S={s0,s1,…,s2t}是由语言术语组成的集合, 且满足: (1) 逆运算neg(si)=sj,i+j=2t;(2)有序性:si≤sj⟺i≤j,且当sj≥si时,最大算子max(si,sj)=sj;当si≤sj时,最小算子min(si,sj)=si,满足上述条件的集合S称为语言集,2t+1为语言集S中语言术语的个数。
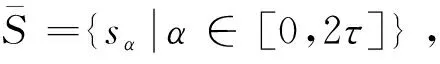
(1)si⊕sj=si+j;(2)λsi=sλi;(3)当j>i时,sj>si。
2.2 犹豫直觉模糊集

2.3 犹豫模糊语言集
定义3[13]设X={x1,x2,…,xn},si∈S,则定义在X上的犹豫模糊语言集HS={(xi,MS(xi)xi∈X)},其中MS(xi)⊂S,MS(xi)中的每个元素表示xi∈X的语言术语评价值隶属度。
2.4 犹豫直觉模糊语言集
定义4[14]定义在X={x1,x2,…,xn}上的犹豫直觉模糊语言集ES={(xi,MS(xi),NS(xi))|xi∈X},其中MS(xi),NS(xi)⊂S,分别表示xi∈X的语言术语评价的隶属度和非隶属度。当X中只有一个元素xi时,简记ES={MS,NS},称其为犹豫直觉模糊语言数。

当人们应用语言信息解决多属性决策问题时, 是利用语言术语下标直接进行计算,在运算过程中可能会造成信息的丢失,为了克服这个问题,Xu Zeshui[19]利用语言术语与其下标之间的严格递增关系,提出了基于语言标度中术语指标的多属性群决策方法,由于在不同语义环境下语言术语对评价对象的表达有一定的差异性,为了刻画这种抽象程度的差异性,可以利用语言尺度函数对不同语义环境下的语言术语赋予确定的数值。语言尺度函数的灵活性以及描述不同语义环境下评价对象的差异性等优点,使它在实际中有着广泛的应用。
定义5[19]设S={s0,s1,…,s2t}为语言集,si∈S,如果存在严格单调的递增映射f:si→θi,
(i=0,1,,…,2t),则称f为语言尺度函数。常用的语言尺度函数有以下三种[20]:
(1)f1(si)=θi=i/2t(i=0,1,…,2t),θi∈[0,1]
(2)f2(si)=θi=
(3)f3(si)=θi=
当语言集S为七值语言集时,此时语言尺度函数f2(si)中a通常取值为1.37,语言尺度函数f3(si)中ξ,η通常取值为0.88[21]。
为对不同的直觉模糊数进行比较,Xu Zeshui[22]基于直觉模糊数的得分函数和精确函数提出了直觉模糊数的比较法则。这种比较方法得到了广泛的推广,在Xu Zeshui[22]的基础上,Faizi等[23]提出了犹豫直觉模糊语言数的得分函数,精确函数以及犹豫直觉度函数。
定义6[23]设S={s0,s1,…,s2t}为语言集,ES={MS,NS}为某一犹豫直觉模糊语言数,其得分函数为S(ES)=s(MS)-s(NS),精确函数为A(ES)=s(MS)+s(NS),犹豫直觉度函数为
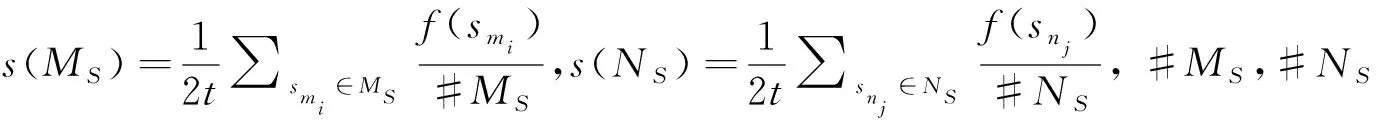
基于犹豫直觉模糊语言数的得分函数和精确函数,Faizi等[23]给出了两个犹豫直觉模糊语言数ES1,ES2的比较法则:
(1)如果S(ES1)>S(ES2),则有ES1≻ES2;
(2)如果S(ES1)=S(ES2)且A(ES1)>A(ES2),则有ES1≻ES2;
(3)如果S(ES1)=S(ES2)且A(ES1)=A(ES2),则有ES1=ES2。
3 基于犹豫直觉模糊语言集均值-标准差的偏好距离
基于距离测度的决策方法是多属性决策问题的一种重要决策方法,常用于分析两个评价对象集合的差异。当两个犹豫直觉模糊语言集的得分函数和精确函数都相等时,此时无法利用Faizi等[23]提出的法则对它们进行比较,但利用距离测度能很好地解决这个问题。有学者对犹豫直觉模糊语言集的距离测度进行了研究,如Beg和Rashid[14]提出了犹豫直觉模糊语言集的包络距离测度:
定义7[14]定义X={x1,x2,…,xn}在上的犹豫直觉模糊语言集A的包络可以表示为:env(A)={(xi;[min(MS(xi)),max(MS(xi))],[min(NS(xi)), max(NS(xi)]xi∈A)},为了方便,将env(A(xi))=[min(MS(xi)),max(MS(xi))],[min(NS(xi)),max(NS(xi)]记为犹豫直觉模糊语言集的包络元素。

例 1 设EA(x),EB(x)和EC(x)为三个犹豫直觉模糊语言数,EA(x)=([s6,s6],[s1,s2]),EB(x)=([s5,s5],[s2,s2]),EC(x)=([s6,s6],[s4,s4]),由Faizi等[23]的比较法则,有EC(x)EB(x)EA(x),则EA(x)与EC(x)的偏差大于EB(x)与EC(x)的偏差。
而由Beg和Rashid[14]定义的距离测度,有d(EA(x),EC(x))=|6-6|+|6-6|+|1-4|+|2-4|=5;d(EB(x),EC(x))=6,即d(EA(x),EC(x)) 这时EA(x)与EC(x)的偏差小于EB(x)与EC(x)的偏差。由Beg等[14]定义的距离来看,显然不满足:当EC(x)⊆EB(x)⊆EA(x)时,d(EA(x),EC(x))≥d(EB(x),EC(x)),d(EA(x),EC(x))≥d(EA(x),EB(x))。 我们可以看到,Beg和Rashid[14]定义的距离测度只考虑了隶属度的最大值和最小值,并没有考虑其它语言术语评价值的信息,同时它也忽略了犹豫模糊集多值评价的显著特点;另一方面,该距离的计算是直接运用语言术语评价值的下标,这不仅失去了语言术语表达实际问题的灵活性,而且也没有考虑不同语义环境下语言术语评价值的差别。 为克服上述距离的不足之处,基于语言尺度函数,我们来定义犹豫直觉模糊语言集均值-标准差偏好的Hamming距离。 定义9设两个犹豫直觉模糊语言数为ES1={MS1,NS1}和ES2={MS2,NS2},基于犹豫直觉模糊语言数均值-标准差偏好的Hamming距离定义为: α,β为非负常数,且α+β=1;Emi,Eni?(i=1,2)分别为xi的隶属度和非隶属度的均值;Smi,Sni(i=1,2)分别为xi的隶属度和非隶属度的标准差;#MS1,#NS1, #MS2,#NS2分别为对应集合中元素的个数,f(·)为语言尺度函数。 定理1设ES1={MS1,NS1},ES2={MS2,NS2}和ES3={MS3,NS3}为犹豫直觉模糊语言数,基于两个犹豫直觉模糊语言数均值-标准差偏好的Hamming距离满足以下性质: (1)0≤d(ES1,ES2)≤1;(2)d(ES1,ES2)=d(ES2,ES1);(3)d(ES1,ES2)≤d(ES1,ES3)+d(ES3,ES2)。 (2)证明: ∵Em1-Em2=Em2-Em1,En1-En2=En2-En1,Sm1-Sm2=Sm2-Sm1,Sn1-Sn2=Sn2-Sn1, ∴d(ES1,ES2)=d(ES2,ES1)。 (3)证明:∵Em1-Em2=Em1-Em3+Em3-Em2≤Em1-Em3+Em3-Em2; 同理En1-En2≤En1-En3+En3-En2, Sm1-Sm2≤Sm1-Sm3+Sm3-Sm2,Sn1-Sn2≤Sn1-Sn3+Sn3-Sn2; (3.1) (3.2) 由(3.1)和(3.2)式可得:d(ES1,ES2)≤d(ES1,ES3)+d(ES3,ES2) 例 2 利用定义9中的距离继续考虑例1。 我们定义基于犹豫直觉模糊语言集均值-标准差偏好的Hamming距离如下: α,β为非负常数,且α+β=1;Emji,Enji(j=1,2)分别为xi的隶属度和非隶属度的均值;Smji,Snji(j=1,2)分别为xi的隶属度和非隶属度的标准差;#MS1i,#NS1i, #MS2i,#NS2i分别为对应集合中元素的个数,f(·)为语言尺度函数。 与定理1的证明方法类似,容易证明d(EA1(x),EA2(x))满足定理1中的三条性质。 下面我们将给出基于犹豫直觉模糊语言集均值-标准差偏好Hamming距离的TOPSIS和TODIM的多属性决策方法。 TOPSIS方法是多属性决策过程中一种经典方法,它利用各方案与正理想解和负理想解的距离来对评价对象进行排序[16,24]。最好的评价方案离“正理想解”距离最近,同时离“负理想解”距离最远,反之为最差。TOPSIS方法的优点是考虑了不同属性的类型,通过综合评价指数来刻画评价方案的优劣,计算简便,可以很快地得到方案的排序结果;该方法的不足之处是依赖于距离测度,使用不同的距离测度可能得到不同的排序结果。基于犹豫直觉模糊语言集均值-标准差偏好Hamming距离测度的TOPSIS方法具体步骤如下: 步骤1.给出犹豫直觉模糊语言决策矩阵ESt(t=1,2,…,k); 步骤2.对k个犹豫直觉模糊语言决策矩阵进行聚合,得ES=(ESij)i=1,2,…,mj=1,2,…,n, 步骤3.确定正理想解ES+和负理想解ES-;对于效益型J1和成本型J2两种属性,正理想解和负理想解分别可以表示为: ES+={maxESi1,maxESi2,…,maxESin},j∈J1,i=1,2,…,m;ES-={minESi1,minESi2,…,minESin},j∈J1,i=1,2,…,m; ES+={minESi1,minESi2,…,minESin},j∈J2,i=1,2,…,m;ES-={maxESi1,maxESi2,…,maxESin},j∈J2,i=1,2,…,m;其中maxESij,minESij(i=1,2,…,m;j=1,2,…,n)由Faizi等[23]的比较法则确定。 步骤5.计算每个方案的综合评价指数Hi=di-/(di++di-); 步骤6.对方案进行排序:综合评价指数越大,相应的方案越优。 TODIM方法是一种基于前景理论的多属性决策方法,是通过建立排序值函数计算备选方案的优势度来对方案进行排序,这种方法可以有效地根据决策者的心理行为处理多属性决策问题中的不确定信息[25]。其优点是根据决策者的风险偏好来调整计算过程中的参数,做出符合决策者心理的决策结果[26],不足之处是参数取值条件的复杂性。对于4.1节中所考虑的决策问题,基于犹豫直觉模糊语言集均值-标准差偏好距离的TODIM方法步骤如下: 步骤1.给出犹豫直觉模糊语言决策矩阵ESt(t=1,2,…,k); 步骤2.对k个犹豫直觉模糊语言决策矩阵ESt进行聚合; 步骤3.对聚合决策矩阵ES标准化,多属性决策问题中,属性有效益型J1和成本型J2,通常可以将决策矩阵ES=(ESij)m×n标准化为 其中neg(MSij,NSij)为语言集的逆算子。 步骤4.计算属性的相对权重,根据参照准则Cl(通常选取属性权重最大的准则作为参照准则),对于给定的每个属性权重ωj,计算它们相对于参照属性Cl的相对权重ωj*=ωj/ωl; 步骤5.计算优势度矩阵,在属性Cj下方案Ai优于Ap的优势度φj(Ai,Ap)为 其中θ表示决策者对损失的敏感程度,θ越小表示决策者对损失的规避程度越高,具体的值可根据实际问题进行选择;q(q≥1)为控制变量,根据决策者的偏好决定其值。 步骤8.对方案进行排序:综合排序值ζ(Ai)越大,方案越优。 为了说明本文提出方法的可行性和有效性,我们采用Faizi等[23]中的实例和数据。 假设某一单位招标建筑商修建办公大楼,他们收到四家不同建筑商A1,A2,A3,A4的方案。为了选择一家合适的建筑商,单位拟从建筑花费C1,建筑材料C2,建筑进程C3,技术风险C4和合约保证C5五个方面来对四家建筑商的方案进行决策。三个专家(D1,D2,D3)构成的评审组对四个方案用七值的语言集S={s0:非常差,s1:差,s2:较差,s3:一般,s4:好,s5:较好,s6:非常好}从五个方面来进行综合评价,选择一家最优的建筑商。五个属性对应的权重为ω=(ω1,ω2,ω3,ω4,ω5)=(0.2,0.4,0.2,0.1,0.1)T。 步骤1.专家的评价既表达了方案Ai在属性Cj下的隶属度,又表达了非隶属度,此时用犹豫直觉模糊语言集表达相关信息更为合适,对应的决策矩阵见(表1~表3): 表1 第一个专家的决策矩阵 表2 第二个专家的决策矩阵 表3 第三个专家的决策矩阵 步骤2.再利用4.1节中的决策步骤,得到四个方案的综合评价指数H1=0.5012,H2=0.3208,H3=0.6677,H4=0.2661;故该单位应选择第三家建筑商修建办公大楼。 类似地,当语言尺度函数为f2si(i=1,2,…,6,t=3,a=1.37),α=0.1,β=0.9,对应方案的排序为A3≻A1≻A2≻A4,此时最优方案为A3;当语言尺度函数为f3(si)(i=1,2,…,6,t=3,ξ=η=0.88,α=0.1,β=0.9),对应方案的排序仍为A3≻A1≻A2≻A4,此时最优方案仍为A3。 步骤1. 与TOPSIS方法类似; 步骤2.利用4.2节中的决策步骤,可得方案Ai的综合排序值:ζ(A1)=0.9568,ζ(A2)=0.1787,ζ(A3)=1,ζ(A4)=0.因此该单位仍应选择建筑商A3修建办公大楼。 类似地,当语言尺度函数为f2si(i=1,2,…,6,t=3,a=1.37),θ=2,q=2时,对应方案的排序为A3≻A1≻A2≻A4,最优方案仍为A3;当语言尺度函数为f3(si)(i=1,2,…,6,t=3,ξ=η=0.88,θ=2,q=2时,对应方案的排序为A3≻A1≻A2≻A4,最优方案与f1(si),f2(si)是一致的。 本文定义距离中的偏好参数α和β分别反映了决策者对语言术语评价值集中性和波动性的不同偏好态度。我们可以根据决策者的偏好态度选择不同的偏好值α(或β)来分析偏好参数的变化对方案排序的影响情况。 在TOPSIS方法中,我们以f1(si)为例,分别令α=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,讨论综合评价指数Hi随α的变化情况,见图1。 图1 TOPSIS方法中Hi随α的变化情况 由图1可以看出,随着α取值的变化,虽然四个方案Hi的大小排序发生了略微变化,但最优方案一直为A3,从一定程度上说明了我们定义距离测度TOPSIS决策方法的稳定性。另一方面风险规避程度越高的决策者α值越大,从图1可以知道,决策者风险规避程度增大时,综合评价指数Hi也增大,但到一定程度Hi将趋于稳定,这也表明了各方案最终的排序结果与偏好参数α的取值无关。 在TODIM方法中,当语言尺度函数为f1(si),α=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,同样我们来讨论综合排序值ζ(Ai)随α的变化情况,见图2。 图2 TODIM方法中ζ(Ai)随α的变化情况 由图2可以看出,随着α取值的变化,四个方案Ai的综合排序值ζ(Ai)的结果并没有发生改变,最优方案一直为A3,说明了α取值变化并不影响方案的最终排序结果,也表明基于均值-标准差偏好距离的TODIM决策方法得到的结果是稳定的。 为了说明基于犹豫直觉模糊语言集均值-标准差偏好距离决策方法的优势,我们与Faizi等[23]中同一实例采用outranking方法所得结果进行比较,见表7。 表7 排序结果的比较 从表中可以看出,Faizi等[20]中采用基于犹豫直觉模糊语言集支撑函数,风险函数和可信度函数的outranking方法所得方案的排序结果与本文基于犹豫直觉模糊语言集均值-标准差偏好距离决策方法所得结果有所不同,主要原因是:outranking方法在评价决策过程中允许使用不完整的评价信息,并且允许偏好之间存在不可比性和非传递性[27-28]。另一方面本文提出的犹豫直觉模糊语言集距离的决策方法是基于均值-标准差进行排序的,明显优于以得分函数和犹豫度函数的outranking决策方法。同时基于犹豫直觉模糊语言集均值-标准差偏好距离的TOPSIS和TODIM决策方法考虑了决策者风险规避的态度,并且两种方法所得的排序结果相同,表明了TOPSIS方法和TODIM方法的可行性和有效性。另一方面,本文定义的距离测度是基于语言尺度函数的,决策者能够根据他们的偏好和实际情况来选择语言尺度函数,这更符合实际情形。 本文定义了犹豫直觉模糊语言集均值-标准差偏好的距离测度,并提出了基于相应距离TOPSIS和TODIM的多属性决策方法来对备选方案进行排序。虽然文中是以实例建筑商招标方案来说明决策方法的可行性,但以犹豫直觉模糊语言集均值-标准差偏好距离的决策方法也能够用于供应商选择、风险投资分析等领域的其它决策问题。同时,我们还会考虑犹豫直觉模糊语言集中每个语言术语评价值出现的频数问题,即我们后面要研究的基于语言尺度函数的概率犹豫模糊语言集和它在实际决策问题的运用。





4 基于犹豫直觉模糊语言集距离测度的多属性决策

4.1 基于犹豫直觉模糊语言集均值-标准差距离测度的TOPSIS方法



4.2 基于犹豫直觉模糊语言集均值-标准差距离测度的TODIM方法

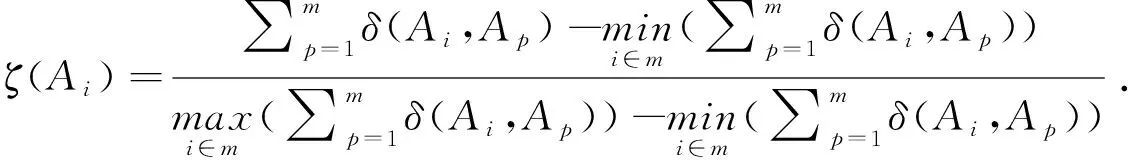
5 数值实例
5.1 基于犹豫直觉模糊语言集均值-标准差偏好距离的TOPSIS方法



5.2 基于犹豫直觉模糊语言集均值-标准差偏好距离的TODIM方法
5.3 偏好参数灵敏度分析

5.4 比较分析

6 结语

