中国股市投资者情绪测度指标的优选研究

刘学文

(烟台大学经济管理学院，山东 烟台 264005)

1 引言

投资者情绪的测度是行为金融学的重点、难点与热点问题[1]之一，各种关于投资者情绪的实证研究都有赖于科学的投资者情绪测度。目前，国内外关于投资者情绪测度的指标可分为单一指标和复合指标。众多学者从各个微观视角，建立了多达上百个各具特色的单一情绪测度指标，“百家争鸣”[1]，丰富了该研究，但这些指标随机零散，良莠不齐，不同的指标可能仅仅反映了投资者情绪的某一方面，往往不适用于测度整个股票市场的情绪。后来，国外的Baker和Wurgler[2]使用封闭式基金折价率、换手率、IPO 数量、IPO 首日收益率、新股发行占比以及红利溢价六个单一代理变量，通过主成分分析法构建了复合型的情绪测度指数(简称BW法)，随后黄德龙等[3]采用了中国三个代理变量，易志高和茅宁[4]采用了中国六个代理变量，都借鉴了BW法来测度情绪，Kim和Ha[5]采用韩国十个代理变量，Liao等[6]采用美国十个代理变量，也沿用了BW法来测度投资者情绪。

可见，BW法已成为目前学术界测度股市整体投资者情绪的主流方法[7-8]。但BW及其追随者们，在用主成分分析法构建投资者情绪指数时所采用的指标各不相同，主观随意性很强，对入选指标并未按照一定的标准进行合理性的甄别，对选用指标的个数也未做出优选，这样仅仅基于主观选择得到的指标构建的综合情绪测度指数，其科学性值得商榷。我们认为，复合投资者情绪指数的构建不应该只采用某几个凭主观分析得到的单一情绪测度指标，而应采用一定的科学方法首先对众多备选的单一情绪测度指标进行优选，去伪存真，去芜存精，然后再基于优选出的情绪测度指标，通过主成分分析法或其他方法来构建反映整体市场情绪的综合情绪指数。而学术界对于如何更为规范性地选取情绪测度指标，尚缺乏科学、统一、标准的方法[9]，这将成为本文研究的主要内容。

本文将基于有限理性的假设对广义投资者情绪的涵义进行理论分析，确定投资者情绪测度指标优选的原则，按照这些原则建立一套系统的指标优选方法——“倒金字塔滤网模型”，对单项情绪代理指标进行层层过滤优选，然后对优选出来的指标进行动态分析，最终基于优选出来的指标采用主成分分析法重新构建中国股市整体的投资者情绪指数，并分析其优越性。以期为投资者情绪综合指数构建前的指标优选提供方法参考，为综合情绪测度指数的构建准备好客观优选出来的指标，这样基于优选后的指标构建的综合情绪指数也可以得到优化，以便更好的解释股市整体投资者的情绪，更好的进行其他与投资者情绪有关的研究与实践。

2 投资者情绪反馈环模型

行为金融学中的投资者情绪的涵义自一开始就基于对标准金融理论的批判而被置于非理性的假设前提之下。实际上，Baker和 Wugrler[2]、Brown和Cliff[10]、Kumar和Lee[11]均认为情绪并非完全等同于非理性，还包含着理性成份，有限理性是理性与非理性交织共存的状态，这一点也得到了Simon[12]、Kahneman[13]两位诺奖得主的理论支持，他们都认为理性和感性相容共存、共同影响着行为人的行动。投资者情绪涵义不仅是指基于非理性假设的狭义界定[10]，也可以是指基于有限理性假设的广义界定。该广义涵义与心理学当中情绪的涵义是吻合的，心理学中的情绪是指人对客观事物的态度体验及相应的行为反应[14]，投资者面对的客观事物既包括经济因素也包括非经济因素。

行为金融理论基于心理学原理，将投资决策过程视为心理情绪过程[15]。行为金融著名学者希勒提出了“股市的反馈环理论”[16]，著名投资大鳄索罗斯提出了“反射性理论”[17]，学术派和实战派的这两位代表所提出的理论也可称作“投资的反馈环理论”，认为股票市场中存在着“客观信息——认识——行为”这样一个连续不断、循环往复的并伴随着羊群行为的环形反馈系统。

基于有限理性假设和投资反馈环理论，我们构建了“投资者情绪反馈环模型”(图1)。该模型囊括了上述文献综述中所提到的学者们创建的各种单项情绪测度指标，凡是与投资者或潜在投资者的投资决策行为有关的任何变量均有可能做为投资者情绪测度的指标。这是本文研究的立足点。

图1 投资者情绪反馈环模型

3 投资者情绪测度指标优选的原则和方法

当前学界比较认可的情绪测度方法是Baker 和Wurgler[2]应用的主成分分析法。该方法所需备选单项指标往往是通过经验来确定，且指标选择范围较为局限，这就使得由该方法构建的综合情绪测度指数缺乏客观性与全面性，故很有必要对更多的情绪测度单项指标进行科学优选。本文拟构建一套投资者情绪测度指标优选的方法，来补充完善这一个缺失的环节。投资者情绪测度指标的优选是指在众多观测指标变量中，按照一套规范的指标优选方法结合定性分析，选择相关指标，剔除冗余，用最少的指标显著表达尽可能全面的投资者情绪信息。

3.1 投资者情绪测度指标优选的原则

影响投资者情绪的指标因素众多，为采用科学的方法选取可做为主成分分析的备选指标，为该方法做好前期的指标准备工作，需遵循以下原则[3]。

(1)开放性原则

任何与投资者或资本市场有关的行为，都有可能会影响到投资者的情绪，情绪测度指标众多，以后或有新的指标出现，指标优选时应该遵循开放性的原则，任何新生指标均可纳入该优选体系被检验选取，以保证投资者情绪测度的全面性和先进性。

(2)相关性原则

该原则有两层含义：第一，任何指标均应与股票市场具有一定的相关性，毫不相关或者相关性很低的指标不应被选取；第二，各类指标中的子指标应该与该类中其他指标具有良好的相关性，以保证这些指标的代表性。

(3)可得性原则

一些曾被认为可反映投资者情绪的单项指标由于各种原因导致数据停止提供或数据不易获得，应予剔除，以保证情绪测度指标可以量化[7]。

(4)替代性原则

在对情绪测度指标进行筛选时，要对完全相关的指标进行无损替代，通过聚类将反映信息相同的指标聚为一类，这样不同类别的指标反映不同的数据特征，保证了从不同类筛选出的指标反应信息不重复，以避免信息的重复冗余。

(5)低信息成本原则

通过上述相关分析剔除不相关的指标、替代完全相关的重复指标，通过聚类、降维减少指标个数，通过主成分分析剔除因子负载小的指标，保证最终优选出的指标对评价结果有显著影响，用尽可能少的指标个数反映尽可能多的原始信息。

(6)兼顾客观性与主观性

通过技术手段更科学的定量优选情绪代理变量，同时加入人为的丰富经验确定最终的指标变量。既可避免过渡依靠纯技术方法的局限性，也可避免仅依靠人为选择的主观性。

3.2 投资者情绪测度指标优选的方法

基于上述理论依据，我们构建了开放式的“倒金字塔滤网模型”这样一套方法系统(如图2所示)，层层过滤，对投资者情绪测度指标进行优选。

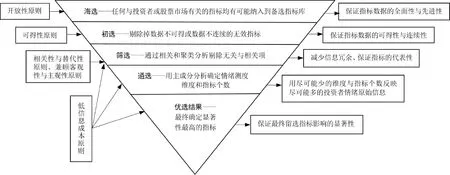
图2 投资者情绪测度指标优选的倒金字塔滤网模型

3.2.1 基础数据准备——海选与初选

由上述投资者情绪反馈环模型及开放性原则可知，凡是与投资者或潜在投资者的投资决策行为有关的任何指标包括各种经济类和非经济类指标，均可纳入备选指标体系。如此，海量备选指标将形成备选指标库，从而保证投资者情绪测度的全面性和先进性。但由于各种原因，备选指标中有些指标的数据无效，如数据不可得或数据不连续，故应先对海选形成的备选指标进行初选，剔除那些数据无效的指标。

经过海选，得到备选指标库Au×n，如式1所示，具有u个维度的备选指标，样本长度为n个。

(1)

然后，Au×n指标库经过初选，剔除了不可得或不连续的指标，得到Bv×n指标库。

3.2.2 剔除无关与相关项——基于相关性与聚类分析的指标筛选

投资者情绪与投资者所投资的股票市场相互关联，因而用于测度投资者情绪的变量应与股票市场相关。可通过相关性分析剔除无关指标，以保证所选指标的相关性、代表性。可以通过计算所有潜在指标与股指或股指收益率的相关系数，以判定其相关性、剔除无关指标。分别将股指和股指收益率与Bv×n指标库中的指标计算相关系数rxy，其计算公式为：

(2)

其中，xi(i=1,2，…,n)为Bv×n指标库中的指标，yij(i=1,2，…,n；j=1,2)为对应时间段内的股指或股指收益率。

相关系数一般都是利用样本数据计算的，因而带有一定的随机性，样本容量越小其可信程度越差。因此，需要计算相关系数的t值及伴随概率检验。t统计量服从n-2个自由度的t分布，并计算其伴随概率。若t值不显著，则认为其与股票市场无关。可以结合t值与相关系数的绝对值大小，留选指标。t值的计算公式为：

(3)

首先考虑t值的界限，在满足5%或1%界限的前提下，若计算得到的相关系数│r│大于所设定的相关系数的阈值│r0│，则此指标可以留选。相关系数阈值r0取值范围为-1到1之间，因而│r0│的取值范围为0到1。│r0│的值越小，留选的指标数目越多，一般取0.3为宜。

经过剔除无关项后，得到CW×n指标库。剔除掉数据不可得不连续、无关指标之后，需要进一步通过聚类分析与相关分析剔除相关项进行降维处理，从而缩减指标数量、减少冗余信息。通过聚类分析(泊松相关系数法)，可以忽略掉数据的单位影响，避免“大数吃小数”的可能性，并能够将一批样本数据按照其在性质上的亲疏程度在无先验知识的情况下自动进行分类而不必事先给出一个分类的标准，保证了降维的客观性。通过聚类分析可以将具有相似特征的变量归为一类，并按照变量的特征区别得到全局变量的分布状态。通过观察聚类分析树状分支图，可以直观的观察到各种变量的亲疏程度。当两个变量高度相关，甚至相关系数为1时，可以认为，这两个变量为同一变量，应予剔除。其目的是简化指标体系、减少系统的冗余信息量。在删除相关系数为1 或者接近于1的指标时，可以人为选择，尽量保留那些数据更易得的指标、原始性更好的指标、直接而非间接指标。具体步骤可借鉴刘学文等[18]的研究。

3.2.3 确定情绪测度维度与指标个数——基于主成分分析的指标遴选

经过上一步的指标筛选，根据聚类分析树状图，能够直观分析各个指标之间的相互关系。此时所有的留选变量都可以作为潜在情绪代理变量，但仍有冗余信息，且不容易确定选择哪几类指标。当前，尚未有学者研究应该选择多少个维度、多少个变量来进行情绪测度。借助于主成分分析，确定留选变量数目，能满足数学上信息精度，以便在尽可能多的信息特征下进一步简化系统的复杂性。主成分分析，是将复杂数据进行降维的一个有力工具，其本质是将高维度数据经过一系列的线性变换最后确定几个综合的变量，而这几个综合变量可以反映原来多个变量的大部分信息。最后所确定的综合变量互不相关，这样保证了综合变量所含的信息互不重叠。通过主成分分析中信息含量的多少与特征根的大小，结合上述聚类分析树状图谱，能够很直观的观测并确定测度维度的个数与其变量集合，能够确知都有哪些变量是在同一个维度来测度情绪，以便进一步剔除同一维度中的相似变量，减少冗余信息。一般情况下，选择信息含量大于85%或者是特征根大于1的主成分个数。此处，我们选择主成分特征根大于1，或者为了使其包含更多的信息，也可以接近于1作为标准。主成分分析的模型为[19]：

Fi=αi1X1+αi2X2+…+αiwXw,i=1,2,…,p

(4)

其中，p为主成分的个数，w为指标个数，CW×n中有w维度的指标，因而XW为第w个指标(w=1,2，…,w)，Fi为第i个主成分(i=1,2，…,p)，且p≤w；αiw为对应第i个特征值的特征向量的第w个分量。

特征根与累计贡献率的计算步骤为：

(1)计算CW×n的相关系数矩阵RCW×W；

(2) 计算矩阵RCW×W的特征值λj(j=1,2，…，w)，λj表示第j个主成分Fj所解释的原始指标数据的总方差，则主成分Fj对原始指标数据的方差贡献率ωj为：

(5)

经过上述主成分分析，可以确定CW×n指标库中情绪的主要维度方向，结合聚类分析图谱，使得指标归类更准确，进而获得重新排序的DW×n指标库与情绪主要维度个数z。

3.2.4 确定情绪测度指标优选结果

上一步确定的各个情绪测度维度中的指标在各个维度上的影响力各不相同，应尽可能多的选择各维度指标集合中最重要的指标，舍弃影响力小的指标，进而优化选择情绪的代理变量。我们只要将在每一维度变量集合中的最优指标进一步确定下来，即可最终完成情绪测度指标的优选。在各维度集合中，优选指标的方法可采用变异系数法。情绪测度指标的变异系数反映该指标在投资者情绪测度中的表征能力。通过变异系数筛选出同一维度中鉴别能力最大、即信息含量最大的指标，保证了筛选出的指标对投资者情绪测度的影响最为显著。变异系数越大，表明该指标在投资者情绪测度中的分布变异性越大、信息含量越大，指标的信息分辨能力越强，影响越大，应予保留；反之，指标的信息分辨能力则越弱，应予以剔除。变异系数的计算公式为[20]：

(6)

(7)

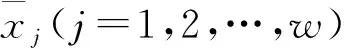
将指标库CW×n通过聚类分析，分成z类维度后得到DW×n，选择各维度中变异系数CV值最大的指标，作为最终留选指标，最终得到Ez×n。

4 实证分析

4.1 指标的海选与初选

图2所示的倒金字塔滤网模型是一个开放的系统，任何指标都可以做为初选指标纳入该体系备选，基于图1的投资者情绪反馈环模型我们将所有投资者情绪指标划分为非交易类和交易类两大类，并做了进一步的分类(如表1所示)，基于该分类我们广泛搜集数据资料海选了62个指标，以保证纳入滤网模型的指标的全面性，考虑到数据的可得性、连续性，同时也考虑到指标的客观性，我们保留了其中数据连续可得且有文献出处的33个指标，基本上涵盖了各大类单项情绪指标。Baker和Wurgler[2]构建综合情绪指数时所用的数据为年度数据，适用于欧美成熟市场，中国的股票市场正处于发展当中，投资者情绪波动相对来说更为明显，故我们所选情绪测度指标的数据均为月度数据[4]，具体指标及其数据来源详见表1。我们选取了尽可能长的2005年1月到2015年12月的时间做为样本区间。

表1数据分类及来源与无关指标删除过程

需要说明的是，许多研究表明[6,27-28]投资者往往会根据过去的股票收益率来预测股票的未来收益，股价指数和股价指数收益率也可做为情绪代理变量之一。对于股指的选取，我们通过计算分析上证综指、深证综指、上证A股、深圳成指之间的相关性可以发现，其相关程度都比较高，并且从归一化数据来看，其走势也大体相同，从中选取哪一个股指当做最终股指都是等价的。本文直接选取投资者关注度较高的上证综指及其收益率做为研究对象。

4.2 基于相关性分析与聚类分析的筛选

经过基础准备工作后，得到了33个变量进入筛选阶段。需要进一步将与股票市场相互作用小的、无关的变量剔除。通过计算各指标与股指和股指收益率的相关系数，可以得到无关程度与显著性检验值，无关指标的删除过程如表1所示。

通过计算可以得到33×2个相关系数和33×2个显著性值。由于海选指标范围非常广泛，指标系统较为复杂，需要更精准的删除无关变量。因此，我们将阈值设定为1%的显著概率，进行严格的筛选。值得说明的是，若想让更多的潜在变量进入下一步的筛选，可以设置更大一些的显著性值概率。通过分析可以发现，在1%显著概率的情形下，相关系数为0.3。得到与上证综指收盘价相关的有19个指标，与上证综指收益率相关的有4个指标，两类指标有重叠，共计22个，有11个无关变量被删除掉。

为了验证所删除的无关变量是否合理，可通过聚类分析得到系统树状图，进一步分析各变量间的分布，明确各变量的亲疏程度。图3为33个情绪测度指标变量的树状分析图谱，后面带“×”的变量为删除的无关变量，共计11个。被删除的变量与上证综指及其收益率不在同一集合内，距离较远，说明不属于一类变量。同时，与上证综指及其收益率距离较近的所有指标都被留选了，表明删除的无关变量是合理的。

图3 33个潜在情绪测度指标的聚类树状图谱

我们将上述22个变量进行聚类分析与相关分析，得到22个变量的树状分析图，并将相关系数最高的几个变量标注在图4中。图4中，22个变量是将无关变量删除以后得到的，可以发现有很多变量聚集在很小的集合中，在这些集合内部他们是高度相关的，其相关系数非常高，甚至完全相关，如换手率与交易量的相关系数为1，类似的完全相关的变量共有6对。事实上，这些相关系数为1的指标高度相关，对情绪的影响是平等的。如交易量与换手率，其本质是一样的，在数学上地位相同，这就需要删除其中的冗余变量，留选时可以根据上文所述原则结合经验主观确定。考虑到保持数据的客观性，此处，我们暂不做删除，留待后面4.4部分根据变异系数删除。

4.3 基于主成分分析的指标遴选

上一步在一定程度上缩减了冗余信息，根据树状分析图谱也能够明确各变量的亲疏状况，但仍有信息冗余，且不知该留选哪些维度的指标、每一维度中应该留选哪几个指标变量。通过主成分分析，可进一步将冗余信息压缩到最小，进而确定测度情绪的内在维度。这里，我们仍将使用22个变量进行分析，以便对上一步的结果进行检验。我们将上述数据进行主成分分析以后，得到结果如表2所示。22个变量经过主成分分析后，可得到22个主成分。主成分的信息含量使用特征根表示，按照降序排列，自上而下，每一主成分的信息含量逐渐减少，累计信息含量逐渐增多，直至100%。例如，当选择第一主成分时，所包含的信息含量为原来的41.594%，当选择前6个主成分时，所包含的信息量为原来的89.419%。

由表2可以发现有22个主成分，说明存在22个情绪测度维度，前16个主成分的累计信息含量为100%，说明只需要16个变量就能无损表达原始信息，其余维度的作用十分微小，甚至为零。因此，存在6个主成分的冗余信息。这里的结果，验证了上一步22个变量中，存在6个完全相关的变量，删除完全相关变量不影响总体信息含量，或者说删除高度相关变量，影响整体信息含量十分微小。根据边际效应原理，随着选取主成分个数的增加，整体信息提取方法：主成分分析。

图4 22个情绪测度指标聚类树状图谱分类、相关系数与变异系数

表2 主成分分析贡献率

主成分特征根方差贡献率(%)累计方差贡献率(%)19.15141.59441.59423.49015.86457.45832.52211.46368.92142.38210.82879.74951.2175.53085.27960.9114.14089.41970.7563.43592.85480.4982.26295.11590.3601.63696.751100.2941.33598.086110.2451.11499.200120.0960.43599.635130.0490.22099.855140.0210.09399.949150.0110.05199.999160.0000.001100.000171.403E-76.376E-7100.000189.902E-104.501E-9100.000195.516E-102.507E-9100.000206.968E-163.167E-15100.000212.193E-169.969E-16100.00022-3.242E-16-1.474E-15100.000

含量逐渐增多，其单个主成分信息含量会逐渐减少。因此，应汰弱留强以确定情绪测度维度。一般情况下，把特征根大于1作为界限标准，当主成分的特征值小于1时，其信息解释度不具有原释能力。谨慎起见，可选择6个主成分，把接近于1的主成分选入，此时的信息含量为89.419%，这意味着存在6个维度测度投资者情绪，包含了89.419%的影响力(原信息量)，由原来的22个指标缩减为6个指标，信息含量仅减少了11%，而单个指标的信息含量却提高为原来的3.3倍。

4.4 优选情绪测度指标

确定情绪测度维度的数量以后，应结合聚类分析树状图谱，剔除同一维度中的相似变量，进一步减少冗余信息。图4中的虚线，将树状分析图分成了6大类，即6个情绪测度维度。每一维度中，又包含多个指标，同一维度中的指标对投资者情绪的影响力是同一方向的。本文采用变异系数法，在每一维度中优选出信息含量最大、最具有代表性的指标，保证优选出的指标对情绪测度具有显著的影响。具体结果如图4所示，其中尾部带“√”的6个指标即新增开户数、上证综指收益率、封闭式基金折价率、IPO流通股数加权的平均收益率、居民消费价格指数、换手率一阶差分，是我们通过倒金字塔滤网模型层层优选后最终得到的优选指标。

5 情绪测度指标优选方法的动态分析

更进一步的，我们通过“移动窗口”滚动计算，对情绪变量进行多次优选，进而证明倒金字塔滤网模型的动态适用性。我们所测度的投资者情绪是整个股票市场关于投资者的中长期的情绪，故我们基于132个时间点以30为时间窗口的宽度，每次移动1个时间点，共计算103次，每次的样本数量为30个时间点，特征根的阈值为1。结果如图5所示，横坐标代表着“移动窗口”计算的次数，共103次，纵坐标对应的是22个变量的名称，小黑点代表着被选中的情绪指标变量，为便于观察，我们将上证综指也叠加放到图5中。

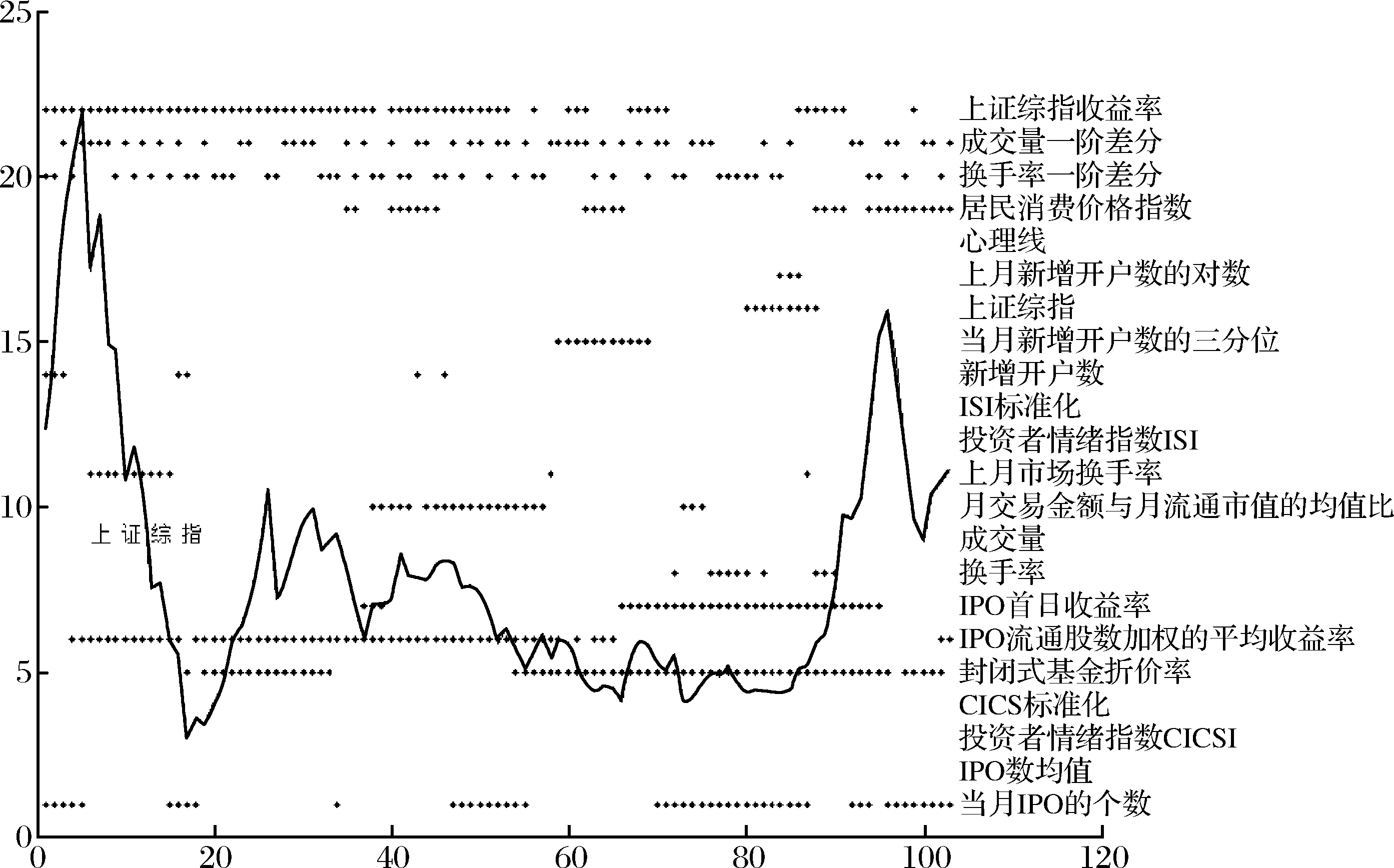
图5 103个移动窗口的投资者情绪测度指标的留选

此处需要说明的是，各变量中存在完全相关的情形，选择完全相关的两个变量是等价的，由于程序计算顺序的原因，会出现随机选择等价变量的情形，因此我们将相关系数为1的变量进行合并统计并置于括号中，得到表3。表3中较稳定的是换手率一阶差分(成交量一阶差分)、上证综指收益率、封闭式基金折价率、IPO流通股数加权的平均收益率、当月IPO的个数(IPO数均值)、IPO首日收益率等几个指标变量，这几个变量既被包含于我们通过倒金字塔滤网模型优选出的六个指标当中，同时除了上证综指收益率之外也被包含于易志高和茅宁[4]在构建复合情绪指数时所选用的六个指标当中。

总之，基于132个时间点的数据采用移动窗口技术进行分析，可以证明倒金字塔滤网模型适用于任何时段的指标优选，情绪测度指标的优选是一个动态的过程，不同时段的情绪测度指标具有多样性，不同的时段应优选出不同的指标来综合测度整个市场投资者的情绪。其中一些指标具有稳定性，一些指标具有非稳定性，他们与股票市场之间的规律性关系尚待进一步探究。

表3 移动窗口内情绪测度指标累计留选次数

6 基于优选指标的优化投资者情绪指数(OISI)的构建

易志高和茅宁[4]进行主成分融合，在出现第一主成分信息含量较低的情况时，为了使得方差解释率达到85%，采用了对多个主成分加权平均的做法。事实上，经过主成分分析之后，n个指标会出现n个主成分，这n个主成分相互垂直互不相关，若进行加权平均处理，会降低第一主成分的占比。一般情况下，只有第一主成分才具有综合评价功能。因此，我们只选择第一主成分来测度情绪，也只有第一主成分才是6个指标对情绪的共同描述，包含了对投资者情绪最多的影响信息。

我们通过荷载矩阵，计算出用上述最终优选出的6个指标所计算的6个主成分融合数值，并计算n个(n=1、2、3、4、5、6)累计主成分数值的和，其中第一主成分与前一个累计主成分数值相同。同时也分别计算了12个变量与上证综指的相关系数，如表4、图6和图7所示，图中所有带星号的加粗折线图均为上证综指。不难发现，单个主成分与股指的相关系数都小于第一主成分；同样，累计主成分的相关系数也小于第一主成分的相关系数。因此，我们选择第一主成分来测度投资者情绪是正确的，这种方法比累计贡献率达到一定数值后更为精准，而只选择第一主成分同样也是Baker和Wurgler[2]的主张。

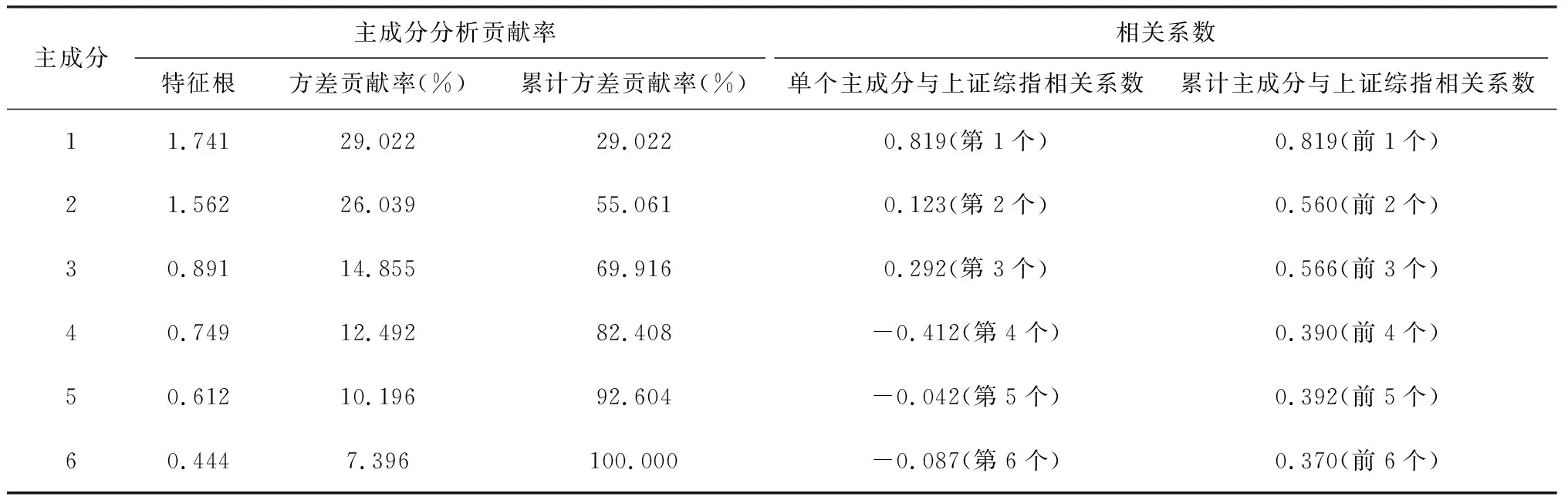
表4 主成分分析贡献率及相关系数

图6 单个主成分与上证综指关系图

图7 累计主成分与上证综指关系图

我们将所选变量通过主成分分析提取第一主成分，再计算对应时间窗口与股指的相关系数绝对值，如图8所示，相关系数的均值为0.6025，在大部分时间窗口是大于均值的，甚至完全相关。这进一步证明了选取第一主成分是可靠的。

图8 移动窗口内的股指与所选情绪测度指标的第一主成分相关系数绝对值

由于本文是对市场整体的长期投资者情绪进行测度，篇幅所限，我们暂不对投资者综合情绪测度指数进行动态分析，就用上述实证分析优选出的6个指标即新增开户数、上证综指收益率、封闭式基金折价率、IPO流通股数加权的平均收益率、居民消费价格指数、换手率一阶差分等做为构建复合情绪指数的基础指标，基于此按第一主成分构建的投资者情绪指数计算公式如下：

OISI=0.72NA-0.163DCLOSE+0.451DCEF+0.76IPOR+0.662CPI-0.51TUR

(8)

图9中我们采用经倒金字塔滤网模型优选出来的指标构建的优化投资者情绪指数OISI(Optimized Investor Sentiment Index)，与图10中应用同样方法但采用未经优选的指标构建的投资者情绪综合测度指数CICSI相比，有两个明显的差异：第一，OISI与上证综指的相关系数为0.8186；CICSI与上证综指的相关系数为0.6435，我们采用优选后的指标构建的综合情绪指数与上证综指的相关系数更高，与股票市场的关系更密切，一定程度上可以说明我们用优选后指标构建的情绪指数更优；第二，CICSI指数在2009年9月份与2010年4月份附近的两个峰值高于2007年7月份附近的峰值，说明2009、2010年这两个时点附近的投资者情绪比2007年7月份附近的还要高涨，而我们构建的指数OISI在这两个时点附近的峰值远低于2007年7月附近的峰值，恰好相反。事实是，2007年7月份处于中国股市上涨异常猛烈的一次大牛市的高峰区域，此时股市整体的投资者情绪异常高涨，这一点尽人皆知。而2009年9月份和2010年4月份处于2008年中国股市下跌速度和幅度都异常巨大的大熊市后的反弹期，反弹的高度有限，股市历经暴跌后，投资者亏损累累，投资信心遭受了严重的打击，即便股市反弹，投资者信心的恢复也是一个缓慢艰难的过程，此时的投资者情绪显然不可能比2007年7月份的“疯牛”行情中的投资者情绪还要高涨。可见，我们采用优选后的指标构建的综合情绪指数OISI显然更符合股票市场投资者情绪的实际情况。

图9 OISI与上证综指关系图

图10 CICSI与上证综指关系图

7 结语

本文通过文献梳理发现投资者情绪的单项测度指标众多、良莠不齐，Baker和Wurgler[2]构建情绪综合测度指数所需单项指标在选用时也具有主观随意性，在运用主成分分析法构建综合投资者情绪测度指数之前，缺失的一环是关于情绪测度指标的规范、科学选取。因此我们构建了一套开放式的指标优选方法系统即倒金字塔滤网模型，首先对海选到的指标进行初选，剔除数据不可得不连续的指标，再通过相关性分析剔除无关项、通过聚类分析剔除高度相关项，然后通过主成分分析确定情绪测度维度及其指标个数，最终通过变异系数法确定留选出最为显著的情绪测度指标，这些指标具有全面性、客观性、显著性、代表性、低信息成本的优势特征。基于这些优选出的指标，我们应用主成分分析法构建了投资者情绪综合测度指数，其结果优于应用同样方法但采用未经优选的指标变量建立的综合情绪指数，用优选后的指标构建的优化投资者情绪指数可以更好的解释中国股市的投资者情绪，也更有利于进行其他与投资者情绪有关的研究与实践。

本文的主要贡献在于，构建了倒金字塔滤网模型进行投资者情绪测度指标的优选，弥补了运用主成分分析法构建投资者情绪综合测度指数之前的指标优选这一环节，可普遍应用于投资者情绪测度指标的优选。我们采用主成分分析法确定了投资者情绪测度的维度及每个维度内的指标个数，并用变异系数法最终优选出各个维度内的最终留选指标，为投资者情绪综合测度指数的构建奠定了基础。同时，我们也发现投资者情绪测度指标的优选是一个动态过程，不同的时段应优选出不同的指标来测度投资者情绪，我们提供的倒金字塔滤网模型适用于任何时段的指标优选。不同时段的优选指标结果与股市之间的规律性关系尚待进一步探究。