基于相对财富效用的多阶段投资组合博弈模型

周忠宝， 任甜甜， 肖和录，吴士健，LIU Wenbin

(1.湖南大学工商管理学院，湖南 长沙 410082；2.湖南师范大学商学院，湖南 长沙 410082；3.山东科技大学经济管理学院，山东 青岛 266510；4.Business School, University of Kent, England Kent CT2 7PE)

1 引言

投资组合理论一直是现代金融研究的重要方向之一，旨在有效地配置金融资产，以实现资产组合收益最大化与风险最小化之间的均衡，其具有重要的理论与现实意义。从投资者的分类来说，金融市场中主要包括个体投资者和机构投资者。对于不同的投资者类型，在理论建模上也会存在较大的差异。一般而言，对于个体投资者的研究多数假定投资者在制定决策只与自身风险偏好和市场条件有关，此类问题的建模主要是基于Markowitz的投资组合理论。尽管Markowitz[1]的均值-方差理论为现代投资组合优化奠定了基石，但是从本质上来讲，该理论是一个静态的投资决策问题，然而在实际金融市场中，投资大多是多阶段或动态的过程。到目前为止，关于个体投资者的多阶段投资组合优化研究已经比较广泛，而关于机构投资者的理论建模则没有统一的标准。

不难发现，上述多阶段投资组合优化问题的研究都是基于单个投资者的投资行为，并未考虑投资者之间的影响关系。然而，对于机构投资者(如基金和保险公司)而言，投资者之间相互独立的假定往往是不符合市场实际的。随着我国金融市场的发展，机构投资者力量不断增强。面对行业中众多势均力敌的竞争者，机构投资者在制定策略时需要充分考虑其对手的投资行为，来权衡投资收益与风险。在现实金融市场中，机构投资者不仅关注自身绩效，往往还趋向于比较自身与同行业竞争者绩效之间的差距。以基金管理为例，基金投资者往往会选择排名靠前的基金来进行购买，这就要求基金经理的投资目标不仅是实现自身基金终端财富最大化，同时还要尽可能拉大与同行业中其他竞争者之间的财富差距，使自身绩效表现更为突出，以吸引更多的基金投资者。因此，将机构投资者之间的相互影响考虑到多阶段投资组合优化中具有较强的现实意义，同时这也是本文的主要研究动机。

许多学者根据投资者与其竞争对手的关系，将投资者与其竞争对手的投资行为抽象为博弈问题进行研究。如Browne[22]首先在连续时间模型中研究了两个相关投资者间的零和随机微分博弈。Bensoussan和Frehse[23]使用动态规划方法来解决了非零和随机微分博弈问题，并证明了纳什均衡解的存在性。张卫国等[24]建立了风险投资者和企业的多阶段双方博弈模型，讨论了在最优状态下的融资合约机制选择。Basu和Ghos[25]研究了多种模式下零和随机微分博弈，并将其应用于投资组合优化问题。曹国华和耿朝刚[26]考虑了竞争机制条件下的风险投资机构决策之间的影响关系，并建立了博弈模型，得出纳什均衡解。Leong和Huang[27]运用非零和随机微分博弈理论来分析投资者的资产分配问题。此外，对于市场中存在竞争关系的投资者而言，各自的投资目标不仅仅是投资者自身终端财富最大化，同时也希望扩大自身与其竞争者的财富差距。与传统的投资组合博弈模型不同，Espinosa和Touzi[28]首次运用相对财富效用(所谓的相对财富效用主要是指投资者自身相对财富所带来的期望效用，其中相对财富为投资者自身财富和自身财富与竞争者财富差距的加权平均)来描述此类博弈关系，在连续时间框架下，利用非零和随机微分博弈形式来解决多个相互作用的投资者最优投资决策问题，证明了在指数效用函数框架下投资者之间的纳什均衡解的存在性。基于Espinosa和Touzi[28]的研究思路，Bensoussan等[29]考虑了两个保险公司的相互影响，建立了非零和博弈模型，并给出基于投资-再保险策略的纳什均衡解。之后，许多学者在Espinosa和Touzi[28]在基础进行了各种拓展，其相关文献如：Meng Hui等[30]，Chi等[31]，Guan Guohui和Liang Zongxia[32]，Yan Ming等[33]以及Deng Chao等[34]。

由上述研究不难发现，已有的关于投资组合博弈问题的大部分文献都局限于连续时间优化问题，离散时间的多阶段投资组合博弈的研究甚少。然而在现实的金融市场中，投资者的决策过程和所能观测到的金融数据往往都是离散的，离散时间的投资组合模型能够更加有效地刻画实际投资过程、提供可供操作的投资建议。本文基于Espinosa和Touzi[28]提出的相对财富效用的概念，在离散时间框架下考虑投资者之间的博弈关系，以实现每个投资者相对终端财富期望效用最大化为投资目标，构建多阶段投资组合博弈模型，利用动态规划方法求出最优纳什均衡投资策略的解析解和均衡值函数。最后，本文的仿真分析部分选取了累计经验分布函数和确定性等价两个主要指标来评价策略的绩效[21,35]，分别比较了不同风险厌恶系数、反应敏感系数以及投资阶段变动时的纳什均衡策略和传统策略投资绩效的差异，结果表明纳什均衡策略优于传统策略。该研究拓展了多阶段投资组合博弈理论，对投资者的决策也有一定的指导作用。

2 多阶段投资组合博弈模型的构建

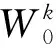
ERt=[E(Rt1),E(Rt2),…,E(Rti)…,

E(Rtm)]′

第i个风险资产在第t阶段的超额收益率Pti=Rti-rt，超额收益率的期望值和协方差矩阵分别记为EPt和Cov(Pt)。

投资者k的效用函数记为Uk，其中k=1,2。基于Espinosa和Touzi[28]以及Bensoussan等[29]提出的相对财富效用的思想，假定投资者的目标是最大化自身相对终端财富，即自身终端财富相对于其他投资者终端财富差距的加权平均。在效用理论框架下，投资者k会选择证券投资决策uk来最大化终端相对财富水平带来的期望效用，则相对财富期望效用可以表示为如下形式：

(1)

(2)

由于投资者在制定策略时考虑竞争对手的表现，据此，用自身财富和自身财富与竞争者财富差距的加权平均值来定义相对财富，其动态转移过程可表示为：

(3)

其中，t=0,1,…,T-1，m≠k∈{1,2}，αk∈[0,1)。

基于如下假设[18]：

1)投资者所处的市场是无摩擦的，并且无买空卖空限制；

2)风险资产收益率服从正态分布，且各阶段相互独立；

3)投资者只在投资初期投入一定财富，而在其后任意投资阶段都不增加资金投入，也不会进行消费。

投资者1的最优策略应满足：

(4)

投资者2的最优策略应满足：

(5)

上述问题的纳什均衡π*=(u1*,u2*)应满足如下条件[36]：

(6)

3 纳什均衡投资策略的求解

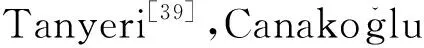
(7)

其中，t=0,1,…,T-1，k∈{1,2}，C>0，1/βk>0，表示投资者k的风险厌恶水平。

定理：假设投资者k的效用函数为负指数型，且在t(t=0,1,…,T-1)阶段，风险资产收益率服从正态分布Ν(μt,Σt)，无风险资产收益率为常数rt。则在给定竞争对手的投资策略时，投资者k的最优值函数及最优投资决策分别为：

t=0,1,…,T-1

(8)

t=0,1,…,T-1

(9)

其中

证明：首先用数学归纳法证明定理对投资者1成立。

1)在第T-1阶段，投资者1的最优值函数可表示为:

(10)

投资者1的最优决策应满足

(11)

则投资者1在第T-1阶段的最优决策与最优值函数分别为:

(12)

(13)

其中

因而，定理在t=T-1时成立。

2)假设定理对于t=j成立，则在第j-1阶段的最优值函数可表示为:

(14)

在资产满足联合正态分布的假设下，投资者1在t=j-1时的最优策略满足如下条件:

(15)

即

(16)

相应的最优值函数为:

(17)

其中

Cj-1

因而定理对t=j-1也成立。

由数学归纳法可知定理对投资者1成立。同理可证定理对投资者2成立。

根据定理以及纳什均衡解的定义，联立下述方程组:

(18)

可得如下推论。

推论：假设投资者k(k=1,2)的效用函数为负指数型，且在t(t=0,1,…,T-1)阶段，风险资产收益率服从正态分布Ν(μt,Σt)，无风险资产收益率为常数rt。则投资者纳什均衡投资策略和纳什均衡值函数分别为：

t=0,1,…,T-1

(19)

t=0,1,…,T-1

(20)

这里

不难发现，当考虑竞争者的投资行为时，投资者的投资策略制定不仅依赖于自身的风险厌恶水平与标的资产的统计特征，同时还依赖于其竞争者的风险态度以及两者对于财富差距的敏感系数。

4 仿真分析

本文仿真分析采用的数据为2001-2015年的四只风险资产年收率和无风险资产年收益率，投资者的初始财富为W0=1，无风险资产收益率rt=1.0400，风险资产在各阶段的均值和协方差矩阵分别为：

E(et)=[1.2567,1.3938,1.2739,1.3989],

其中，t=1,2,…,T。

接下来将比较本文得到的多阶段投资组合纳什均衡策略和传统策略(基于指数效用的多阶段投资组合优化模型对应的最优投资策略)。首先利用蒙特卡洛方法，随机产生105组相互独立且服从正态分布的风险资产收益率，进而比较同一投资者在上述两种优化模型下的投资绩效。本文采用投资者终端财富的累积经验分布函数(ECDF)和Balduzzi和Lynch[35]提出的如下确定性等价(Certainty Equivalent)[21]作为评价指标：

U(CE)=E[U(WT)]⟹CE

以投资者1为例，两种投资策略下投资者1的终端财富累积经验函数分布比较如图1～图5所示(图中Double表示纳什均衡策略，Single表示传统策略)。

图1 投资者1风险厌恶系数变动时的终端财富累积经验分布比较

由图1～图5可知，在不同情况下，纳什均衡策略对应的终端财富累积经验分布均位于传统策略对应的终端财富累积经验分布的右方。这说明对于任一给定的终端财富水平，纳什均衡策略的投资收益超过该水平的概率大于传统策略。此外，如果定义投资者的终端财富值小于零为发生破产。很显然，投资者采用两种策略导致的破产概率非常接近。这就表明，投资者在纳什均衡策略下能够获取较高的收益，而投资者的破产概率并不会明显增加。综合考虑投资收益与风险，不难发现纳什均衡策略优于传统策略。其原因主要在于，当投资者能够观测到竞争对手的特征、战略组合或支付水平等相关信息，投资者对自身的投资行为更为自信，使得自身对风险的偏好程度发生某种程度的改变，更有把握构造高收益资产组合策略，进而实现自身收益最大化和与竞争对手收益差距最大化的投资目标。

接下来本文分两种情况比较两种策略的确定性等价。

(1)1/β1∈{0.2,0.8,2}，1/β2=1，α1=0.2，α2=0.4，T∈{45,…,80}；

(2)1/β1=0.5，1/β2=1，α1∈{0.1,0.5,0.8}，α2=0.4，T∈{45,…,80}。

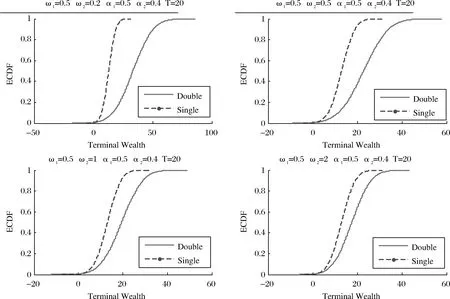
图2 投资者2风险厌恶系数变动时的终端财富累积经验分布比较

图3 投资者1反应敏感系数变动时的终端财富累积经验分布比较

在两种情况下，两模型对应的财富终值对应的CE值如表1和表2所示。

由表1和表2可知，纳什均衡策略对应的CE值高于传统策略对应的CE值，这说明纳什均衡策略在不同情况下的表现均优于传统策略，且随着投资阶段的增加，两种策略的CE值的差距逐渐增大，这也表明纳什均衡策略对于长期投资更有效。其主要原因在于，投资者在每一期都能够运用当前及往期博弈对手的信息，进而调整自身投资策略，且相比于传统策略，纳什均衡策略在每期都能获得较高的收益。因此，投资阶段的增加会导致这种财富差距得到了进一步拉大。

图4 投资者2反应敏感系数变动时的终端财富累积经验分布比较

图5 不同投资阶段的终端财富累积经验分布比较

表1 不同风险厌恶系数和投资阶段下的终端财富CE值比较

表2 不同反应敏感系数和投资阶段下的终端财富CE值比较

5 结语

本文考虑了投资者之间的相互影响，以每个投资者相对终端财富水平的期望效用值最大化为目标，构建多阶段投资组合博弈模型，得到了多阶段投资组合博弈模型的纳什均衡的解析解和均衡值函数。最后通过仿真分析，比较了不同风险厌恶系数、反应敏感系数和投资阶段变动时的纳什均衡策略和传统策略的累积经验概率分布和确定性等价，结果表明纳什均衡策略优于传统策略，从而说明本文所构建的多阶段投资组合博弈模型的合理性和纳什均衡投资组合策略的优越性。本文的研究不仅拓展了现有的多阶段投资组合优化理论，而且对于投资者在金融市场中的决策活动具有一定的参考价值。