已实现波动GAS-HEAVY模型及其实证研究
沈根祥,邹欣悦
(1.上海财经大学经济学院,上海 200433;2.上海财经大学数理经济学教育部重点实验室,上海 200433)
1 引言
波动(volatility)在投资组合选择、风险价值计算等投资决策和管理中具有重要的作用,波动的建模和预测一直是金融计量经济学研究的重点和热点。金融理论和实践中常采用资产价格的方差或者条件方差作为波动计量。自回归条件异方差(ARCH)模型和随机波动(SV)模型是最为常见的波动模型,用于日交易频率或者更低交易频率风险资产价格的建模和预测。随着资产价格日内高频交易数据的获取,已实现波动RV(realized volatility)作为日波动的无偏和一致估计得到广泛应用[1-2]。为利用日内高频数据信息提高波动预测的准确性,Hansen等[3]将RV引入GARCH模型提出已实现GARCH模型(Realized GARCH),Hansen和Huang Zhuo[4]将RV引入EGARCH模型得出已实现EGARCH模型,Shepherd和Sheppard[5]提出基于高频数据的波动预测模型,简称HEAVY(High-frEquency-bAsed VolatilitY)模型。
波动模型设定包括收益模型(也称为一阶矩模型)设定和波动模型(也称为二阶矩模型)设定。尽管在二阶矩模型中加入RV比传统GARCH模型具有更好的波动预测效果,已实现GARCH模型(包括已实现EGARCH模型)和HEAVY模型存在两个不足:一是将一阶矩模型中收益分布设定为正态分布,将二阶矩模型中已实现波动设定为对数正态分布,不能充分刻画收益分布和已实现波动的厚尾性;二是在波动模型中引入RV的方式较为随意(ad hoc),缺乏准则和理论基础。Opschoor等[6]在研究多资产波动模型时,采用向量t分布作为收益的联合分布,矩阵F分布作为已实现方差-协方差矩阵的联合分布,充分捕获资产收益和波动中的厚尾特征,以观测驱动模型设定方法给出波动模型的具体形式,提出一种新HEAVY波动模型。
由于不可观测性,作为波动代理变量的方差可以看作时变参数。Cox将时变参数模型的设定分为观测驱动(observation-driven)和参数驱动(parameter-driven)。观测驱动模型将t期的参数值表示为自回归项和t-1期变量可测函数的和,参数驱动模型则用一阶自回归模型描述参数的动态变化。Creal等[7]在研究观测驱动模型设定时,提出采用观测变量密度函数关于时变参数得分函数形成的鞅差序列构造时变参数模型,称为广义自回归得分(Generalized Autoregressive Score)模型,简称GAS模型,也称为得分驱动(score-driven)模型。Blasques等[8]以Kullback-Leibler距离(简称K-L距离)为准则,从信息理论的角度证明,观测驱动模型中只有GAS模型得出的条件密度函数才能减少和实际条件密度函数之间的K-L距离,即使模型设定错误的情况下仍然如此。Koopman等[9]对文献中常用的两类时变参数模型的预测效果进行比较,发现GAS模型与参数驱动模型的均方误差仅相差不到1%,而由于包含隐变量需要采用数值积分计算似然函数,参数驱动模型估计中的计算困难和计算量远远大于观测驱动模型。
本文对已实现GARCH模型和HEAVY模型进行改进,提出广义自回归得分HEAVY波动模型,简记为GAS-HEAVY模型。收益和已实现波动分布的设定借鉴Opschoor等[6],用波动对收益进行尺度调整得出调整t分布(rescaled t-distribution)作为资产收益分布,更为灵活地捕获收益分布厚尾性和波动时变性,用波动对RV进行尺度调整得出调整F分布作为已实现波动的分布。F分布具有两个自由度,与单自由度分布(如χ2分布)相比,对RV分布的厚尾性和非对称性刻画更为充分,同时F分布的支撑(support)是(0,),满足RV只取正值的限制条件。波动模型的设定采用GAS模型。在给出平稳性条件以及非负性条件后,本文分析了GAS-HEAVY波动模型的性质,并与已实现波动GARCH模型、HEAVY模型和t-GARCH模型进行比较以说明其优越性。蒙特卡罗模拟试验表明,无论数据生成过程是非随机时变波动模型还是随机波动模型,GAS-HEAVY模型的得分驱动设定使其对波动变化的反映更为灵敏,对样本数据的拟合效果显著优于其它模型。
近几年来,国内对采用高频数据建立波动预测模型进行了大量研究。杨科和陈浪南[10]构建自适应非对称HAR-D-FIGARCH模型对上证综指已实现波动进行预测,取得了很好的效果。杨科等[11]将跳跃因素引入模型,构造AHAR-RV-CJ波动预测模型,研究结果表明跳跃对模型预测效果有显著影响。翟慧等[12]以沪深300指数高频数据为样本,比较了HAR模型和GARCH模型的波动预测能力,认为对数形式的HAR-RV-CJ模型对短期、中期、长期波动率的样本外预测都具有最高的精度。吴恒煜等[13]在HAR-RV模型中引入跳跃和结构转换,认为短期内连续波动和跳跃波动对未来波动影响具有显著差异,负向跳跃波动对未来波动的影响更大。吴鑫育等[14]研究了门限已实现随机波动模型,认为加入门限的已实现随机波动模型具有更好的拟合效果。
本文研究的创新之处体现在波动模型的设定上,以具有两个自由度的F分布作为已实现波动的分布,对RV分布特征的捕捉更具灵活性,以得分驱动方法设定波动模型更新项的具体形式,使其对真实波动的拟合更为有效。选取上海证券交易所证综合指数(上证综指)、深证证券交易所成分指数(深证成指)和沪深300指数日收益数据和日内1分钟收益高频数据的实证研究表明,以Hansen的模型预测能力SPA(Superior Predictive Ability)指标为评价标准[15],GAS-HEAVY模型在不同损失函数下的预测能力均明显优于其它模型。本文研究结果为风险资产波动的拟合和预测提供了更为有效的新模型。
2 模型设定

2.1 rt的时变方差厚尾分布
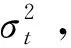
(1)
设d0>2以保证εt存在方差。据此得出给定σt下rt的条件密度为
(2)
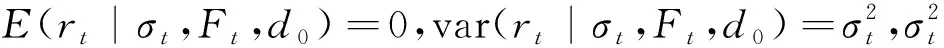
2.2 RVt的时变期望厚尾分布
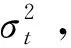
(3)
据此得出RVt的密度函数为
(4)

2.3 波动动态模型设定

观测驱动模型中鞅差序列st的设定十分关键。Creal等[7]将st取作t处观测变量似然函数关于时变参数的得分函数,得出广义自回归得分模型(GAS:Generalized Autoregressive Score):



得分函数为

经计算得出
(5)

St=Sr,t+SRV,t
SRV,t=
(6)
收益模型(1)、已实现波动模型(3)和波动模型(6)构成波动模型
(7)
本文称之为基于高频数据的得分驱动厚尾分布模型,简记为GAS-HEAVY波动模型。
3 GAS-HEAVY波动模型的性质
3.1 平稳性和遍历性


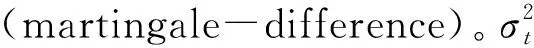


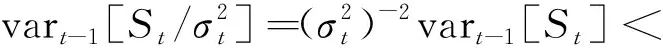
由此得出vart-1[St]<,再由var(St)=E(vart-1(St))得出St方差有限。将St表达式代入合并同类项可以看出,当且0<φ2<φ1时
3.2 与同类波动模型的比较
3.2.1 与t-GARCH模型的比较
GARCH模型中收益rt的分布取作t分布时得到的模型就是t-GARCH模型。由于更能有效捕获分布厚尾性,t-GARCH模型被广泛采用。t-GARCH模型中的波动方程仍然采用标准的GARCH形式,即
(8)
为了比较,不考虑GAS-HEAVY模型中的RVt提供的信息。(7)中St只有收益更新项Sr,t,对应的波动方程为
(9)
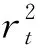
3.2.2 与HEAVY模型的比较
Shephard和Sheppard[5]将已实现波动引入日收益波动模型,提出基于高频数据波动(HEAVY)模型,具体形式为
RVt=(γ/λ)μtξt,ξt~Γ(γ,λ),γ>0
μt+1=ω0+ω1RVt+ω2μt,ω0,ω1,ω2>0,ω1+ω2∈[0,1)


3.2.3 与已实现GARCH模型的比较
Hansen等[3]将已实现波动引入GARCH模型,提出已实现GARCH模型(Realized GARCH),具体形式为
rt=exp(ht/2)εt,εt~N(0,1)
ht=φ0+φ1ht-1+φ2logRVt-1
4 蒙特卡罗模拟实验
通过模拟实验对GAS-HEAVY模型参数极大似然估计性质和模型的波动预测能力进行分析评价。
模拟的第一部分以GAS-HEAVY模型为数据生成过程(DGP:data generating process)生成模拟样本,对模型参数进行极大似然估计,分析模型参数估计效果。给定模型参数值通过(7)式产生模拟样本,然后采用模拟样本对模型参数进行极大似然估计。根据文献和实证研究的有关结果,选取三组参数值进行模拟,第一组参数取值为φ1=0.9、φ2=0.8、d0=7、d1=7、d2=5,第二组参数取值为φ1=0.8、φ2=0.6、d0=6、d1=5、d2=6,第三组参数取值为φ1=0.96、φ2=0.8、d0=12、d1=50、d2=15。模拟的样本量T=1000,按日交易数据计算大体相等于4年的长度。
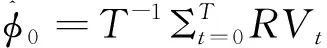
表1中的数据表明,极大似然方法可以较为精确地估计出GAS-HEAVY模型的参数值,波动模型参数φ1、φ2和分布自由度参数d0、d1和d2的估计值都十分接近实际值,且具有很高的显著性。


表1 采用模拟样本的极大似然估计

表2给出了四种不同模型对DGP过程拟合的RMSE及其标准误。

表2 波动模型对模拟样本拟合的均方误差
从表2看出,GAS-HEAVY模型数据拟合的RMSE均值和标准误都远远小于其它模型,拟合效果和稳定性具有明显优势。没有采用RV数据的tGARCH模型拟合效果最差,表明RV对波动模型估计具有信息含量。

图1 模拟数据和不同模型拟合数据时序图
图1给出模拟数据和四种模型拟合数据的时序图。tGARCH与其它模型不具可比性,不再画出。图1表明,已实现GARCH模型和HEAVY模型不能捕捉收益数据的动态变化,原因之一是两类模型中波动模型设定的随意性,对DGP的动态近似效果差。另外一个原因是两类模型中rt和RVt都设定为正态分布或者对数正态分布,不能很好拟合服从t分布和F分布的DGP数据。GAS-NlogN模型中的波动模型采用了GAS模型,对DGP具有较好的动态拟合效果,但由于收益和RV都没有采用厚尾分布,不能很好捕捉数据的厚尾特性,导致其与实际数据具有较大偏差。GAS-HEAVY模型对收益数据动态变化具有较强的捕捉能力,其波动模式与DGP最为接近,收益的t分布和RV的F分布设定充分反映了数据厚尾特征,得分驱动得出的波动模型对DGP模型逼近效果好,同时三个自由度参数也提高了波动模型的灵活性和数据拟合能力。
5 实证分析
为验证GAS-HEAVY模型对实际数据的拟合和预测能力,采用上证综指(000001),深证成指(399001),沪深300(000300)2013年1月至2017年4月共1037个交易日的1分钟高频交易数据和日收盘数据进行实证分析,样本区间包含2015年的股市巨幅波动。采用Barndorff-Nielsen等[18]提出的Realized Kernel方法计算已实现波动率,以消除和减轻市场微观结构噪音和价格跳跃的影响。计算结果表明,样本区间内三大指数的RV峰度都远大于3,体现出明显的尖峰厚尾分布特征。选择χ2分布和F分布作为候选分布对RV进行Kolmogorov-Smirnov(K-S)分布检验。原假设为χ2分布的假设下,三大指数已实现波动K-S检验的p值均为0.00,显著拒绝原假设,原假设为F分布的假设下,三大指数已实现波动K-S检验的p值均为0.06、0.92和0.44,都不能拒绝原假设,表明在RV分布的选择上,F分布比χ2分布更符合实际情况。实证检验结果支持GAS-HEAVY模型对RV分布的设定。
5.1 参数估计
采用三大指数时间序列数据对GAS-HEAVY、HEAVY、R-GARCH和GAS-NlogN(简记为M1、M2、M3和M4)模型实施极大似然估计,并对其拟合和预测效果进行评价。tGARCH模型不作为比较的候选模型。GAS-NlogN(M4)模型采用正态分布和对数正态分布,不再有自由度参数。表3给出模型参数估计值及其标准误(小括号内)。

表3 模型参数估计值及其标准误
注:M4中对应d1的值是RV对数正态分布的方差参数估计值。
从波动模型系数看,GAS-HEAVY模型和HEAVY模型的自回归系数(φ1)高于已实现GARCH模型,三个指数模型的估计结果均体现出这一特征,其原因在于前两个模型对收益和波动都采用了厚尾分布,不时出现的异常观测值被看作来自分布尾部而不是波动水平发生了变化,厚尾分布对波动分布尾部性的控制,凸显了波动的持续性。GAS-HEAVY模型的自回归系数高于NlogN模型,进一步说明厚尾分布的重要性。另一个特征是GAS-HEAVY波动中的更新项系数(φ2)也显著大于HEAVY模型,体现出采用得分驱动设定的波动更新项对收益数据和已实现波动率观测值的利用更加有效,包含了更多影响未来波动的信息。GAS-NlogN模型的更新系数也大于HEAVY模型,进一步说明得分驱动设定波动模型更新项的优势。从三个指数模型的差别看,最为明显的是沪深300指数(000300)GAS-HEAVY波动模型更新项系数(φ2=0.220)明显小于上证综指(0.994)和深证成指(0.996),表明大盘样本股形成的沪深300指数波动更新小于上证综指和深证成指,波动变化更为平稳。

5.2 预测能力比较
预测能力是评价波动模型的常用标准。发现Kupiec的VaR回测检验(backtesting)方法的诸多缺陷后,Hansen[15]提出评价波动模型预测效果的SPA(Superior Predictive Ability)统计量,被广泛采用[12,16]。设模型M0为基准模型,M1…MK为其他K个模型,各个模型样本外预测值计算的损失函数值为Lt,k,t=0,1…,T,定义dt,k≡Lt,0-Lt,k,t=1…T为基准模型与其他模型损失函数之差。dt,k为负表明基准模型预测能力更强。SPA检验统计量定义为:



表4 SPA检验结果
从检验结果看,无论采用哪种损失函数,以GAS-HEAVY为基准模型HEAVY、R-GARCH和GAS-NlogN为对比模型的SPA检验的p值都远远大于5%,尤其是针对沪综指的检验,p值更是高达0.95以上,充分表明GAS-HEAVY模型的波动预测能力强于其它两个模型。以HEAVY模型为基准模型,GAS-HEAVY、R-GARCH和GAS-NlogN为对比模型的检验p值都接近0,拒绝原假设,表明HEAVY模型的预测能力并不比GAS-HEAVY或者R-GARCH模型更强。以R-GARCH模型、GAS-NlogN为基准模型的检验结果与HEAVY为基准模型的检验具有完全相同的结论。SPA检验表明,GAS-HEAVY模型比HEAVY模型、R-GARCH模型和GAS-NlogN模型具有更强的波动预测能力。
6 结语
本文提出一种综合利用日数据和日内高频数据预测风险资产价格波动的模型,分别采用t分布和F分布作为日收益和已实现波动的分布,以期更为充分和灵活地捕捉分布厚尾性;波动模型设定采用观测驱动方法中的得分驱动方法,有效提高了模型对数据生成过程的逼近效率。蒙特卡洛模拟实验显示,本文提出的GAS-HEAVY即使在模型误设的情况下,对数据的拟合效果明显好于同类模型。基于沪综指、深成指和沪深300指数2013.1至2017.4数据的实证分析表明,在两种不同损失函数的SPA检验下GAS-HEAVY模型的波动预测能力显著强于其它同类模型。实证分析中模型参数估计结果表明,以大盘股为样本的沪深300指数波动稳定性和持续性比沪综指和深成指更强,GAS-HEAVY模型设定的合理性,使其对指数波动动态变化的描述和刻画更接近实际。本文提出的波动模型,以其更好的样本内拟合能力和更强的样本外预测能力,为有关理论研究和市场应用提供了新的工具。

