代表点一致性约束的多视角模糊聚类算法∗

张远鹏,周 洁,邓赵红,钟富礼,蒋亦樟,杭文龙,王士同,

1(江南大学 数字媒体学院,江苏 无锡 214122)

2(南通大学 医学信息学系,江苏 南通 226019)

3(Department of Computing,Hong Kong Polytechnic University,Hong Kong 999077,China)

目前,在各个领域,如模式识别、生物信息学、自然语言处理以及社交网络挖掘等,经常会出现同源异构数据,即数据来源(采样对象)是相同的,但是采样的角度(样本特征空间)存在一定的差异,然而又存在一定的关联,这类数据又被称为多视角数据.例如,对人体的血液样本进行采样分析时,检测肝功能的指标特征可以看成一个视角,检测肾功能的指标特征可以看成另外一个视角;又如,在分析银行客户数据集时,人口学信息、账户关联信息以及客户消费行为信息都可以被当成不同的视角.对于多视角数据而言,虽然目前一些学习算法能够从单个视角学习到较为丰富和满意的簇结构信息,但却人为地割裂了各个视角之间的相关性,而这种相关性如果能够加以合理利用,则可以在一定程度上提高算法学习的效率.因此在这种情况下,多视角协同学习技术崭露头角,并且被应用到了领域自适应(domain adaption)[1,2]、迁移学习(transfer learning)[3,4]、主动学习(active learning)[5]、多核学习(multi-kernel learning)[6,7]、多视角分类(multi-view classification)[8]、多视角聚类(multi-view clustering)[9-18]等各个领域.

Cleuziou等人[10]在2009年提出的Co-FKM算法是以经典的FCM框架为基础的多视角协同聚类算法.该算法通过引入协调各视角间空间划分的隶属度约束项,从而使得各个视角的空间划分在算法收敛时最大程度的趋于一致,达到协同学习的目的.实践结果表明,Co-FKM算法具有一定的有效性和扩展性.能够被利用的多视角协同学习的机制有很多,通过调研相关文献,基本上可以分为以下几类.

(1)视角加权机制.视角加权策略在多视角聚类中的应用比较广泛,文献[12,13]中,Jiang等人和Deng等人为了降低某一视角较差的样本分布对算法优化迭代时的干扰,在目标函数中引入香农熵,通过极大熵原理,使得视角的权重偏向于具有较好簇结构边界的视角,从而获取更好的全局划分;Tzortzis等人[14]在CMMs算法[15]的基础上引入视角权重因子πv,并将其视为混合模型下视角的先验概率,然后通过在约束条件下优化一个对数似然函数问题自适应获得视角权重因子值;Chen等人[16]在k-means算法的基础上提出了 TW-k-means算法.该算法利用香农熵进行自适应双层加权,除了对视角加权外,还对每个视角中的样本进行加权.

(2)约束传播机制.该机制的基本原理是:在已知的约束(must-link或 cannot-link)下,通过各个视角不断学习,产生新的约束,并通过映射函数传播至其他视角以进行协同学习.其代表算法是 Eaton等人[17]在Co-EM学习框架下提出的基于不完全约束传播机制的多视角聚类算法.

(3)特征向量一致性约束机制.在基于谱聚类的多视角算法中,这一策略常被采用.最具代表性的是Kumar等人[18,19]提出的基于co-training和co-regularization技术的两种多视角谱聚类算法.两种算法均认为,同一个样本在不同的视角下会被划分到同一个簇中,因此在迭代过程中,通过不同视角下特征向量的一致性约束来使各个视角的划分趋于一致.

这 3种协同学习的机制在不同的应用场景下有着各自的优势.在第(3)种机制中,求解每个视角样本特征向量的过程可被看成是一种降维过程,特征向量从某种意义上来说反映出簇的结构,特征向量一致性约束机制实质上是在多视角协同学习过程中,寻求不同视角下簇结构的一致性.

受此启发,本文提出一种基于代表点一致性约束的多视角模糊聚类算法(multi-view fuzzy clustering with a medoidinvariant constraint,简称MFCMddI).在该算法中,簇的结构通过多个代表点(multi-medoid)来进行刻画,利用视角间代表点一致性来约束协同学习过程,具体来说,

(1)为了获取较为丰富的视角内簇结构信息,采用了基于多代表点的簇结构表示策略,即引入样本权重系数来刻画每个样本成为代表点的可能性.

(2)为了在多视角间协同学习过程中代表点能保持一致性,我们认为,同一样本在不同视角下代表簇的权重系数的差异性最小.基于此,我们首先提出了多视角聚类模型.该模型的目标函数由2项组成:第1项用于产生高质量的视角内划分,该项的优化目标是使得所有样本之间的距离之和达到最小;聚类模型的第 2项用于保持视角间代表点的一致性.为了使整种算法模型易于求解,我们采用视角间两两约束的方式(pair-wise constraint),即所有样本在相邻两个视角下的权重系数的乘积之和达到最大,即代表点差异性最小.

(3)在多视角聚类模型的基础上构建了 MFCMddI算法,并给出了算法的流程和时间复杂度分析.MFCMddI算法可被当作约束优化问题,通过引入拉格朗日乘子和KKT条件,利用求极值的方法得到各个视角下模糊隶属度和样本权重系数的迭代规则,通过迭代寻求各个视角最优的簇结构,并利用集成策略,得到全局划分.

本文的贡献可以概括为以下几个方面.

(1)提出了一种新的多视角聚类模型,该模型综合考虑了视角内的划分质量以及视角间代表点一致性,利用代表点一致性约束进行多视角间协同学习.

(2)在人工集和真实数据集上进行系列实验,实验结果表明,所提出的多视角聚类算法相对于其他算法而言具有一定的优势.

1 多视角聚类模型

1.1 问题描述

1.2 模型构建

基于模糊聚类的思想,所提出的多视角聚类模型的目标是为了获取每个视角的模糊隶属度矩阵Ψm,然后再利用集成策略得到全局的隶属度矩阵Ψ.在学习Ψm的过程中,并非独立进行,还要考虑第 1.1节所陈述的两个问题.因此,我们提出了如下的多视角聚类模型:

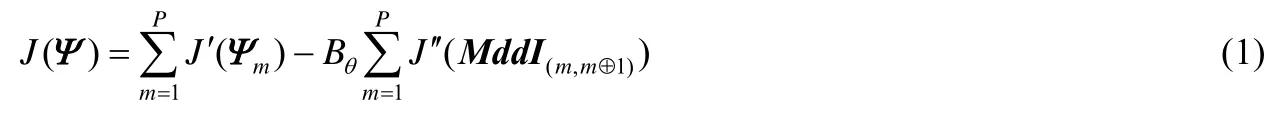
其中,P表示视角数.从公式(1)可以看出,该模型由两部分组成.

对于该模型,我们的优化目标是通过寻找合适的Ψm使得J(Ψ)达到最小.接下来,将对该模型进行进一步的细化.

1.2.1 视角内划分质量

文献[20]指出,用单代表点(one-medoid)来表示一个簇往往不足以刻画簇的结构特征,而基于多代表点(multi-medoid)簇结构表示策略可以获取更多的簇结构信息.为了使这种多代表点策略更加一般化,可以认为数据集中的每个样本都有可能成为簇的代表点,而这种可能性可以量化成[0,1]区间的权重系数,样本的权重值越大,该样本代表其所在簇的可能性越强.因此,为了获取高质量的视角内划分,在最小化样本之间的距离时,还要考虑样本的模糊隶属度和样本权重系数.视角内划分的方法可以通过优化如下的目标函数来获得.

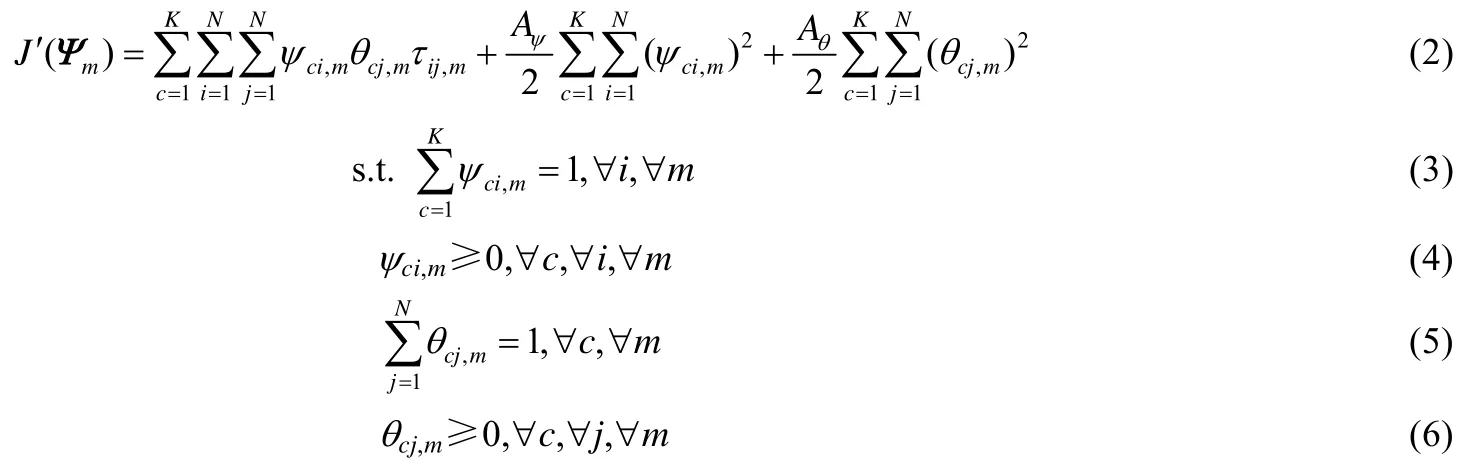
其中,θcj,m表示在视角m下,样本xj代表簇c的程度(即样本权重系数);ψci,m表示在视角m下,样本xj属于簇c的模糊隶属度.从公式(2)中可以看出,J′(Ψm)由3项构成:第1项表示视角m下,所有样本的距离之和;第2项和第3项为ψci,m和θcj,m的二次约束项,目的是提高其泛化能力.Aψ和Aθ为两个大于0的参数,用于保持第1项和第2项、第3项之间的平衡,即控制第2项、第3项对于整个目标函数的贡献.Aψ值越大,样本属于不同簇的隶属度越平滑;同样地,Aθ越大,簇中样本权重系数分布越均匀.

1.2.2 视角间代表点一致性(或差异性)

为了定量表示代表点之间的差异性(medoid invariant,简称MddI),对于簇c中任意的代表点xj,其在视角m和视角m⊕1下的一致性度量标准定义如公式(7)所示.

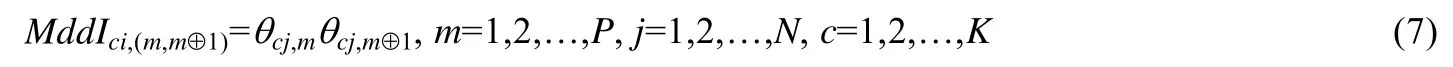
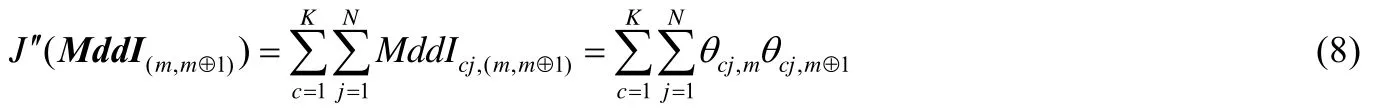
接下来,从理论上探讨最大化视角间代表点一致性(或最小化视角间代表点差异性)可以降低聚类模型在视角上的聚类误差.为了使论证过程简单化且易于理解,我们假设K=2.另外,由于公式(8)和ψci,m无关,可假设不同视角下的对应样本获得相同的聚类标签,每个簇选择一个代表点.我们用Y=〈y1,y2〉表示一个簇在不同视角下的真实代表点标签,用概率P(ml≠ml⊕1)表示视角l和视角l⊕1之间代表点的差异性,其中,y1,y2∈{1,2},1≤l≤P.由于所提出的聚类模型在每个视角下采用的是一种多代表点表示策略,即将所有样本都当成潜在的代表点,通过为每个样本分配权重系数来表示代表性大小.如此,视角内簇结构本质上可由代表点权重系数来刻画[20],因此,P(ml≠ml⊕1)实际上反映的是视角l和视角l⊕1的簇结构差异性.

定义1(有效聚类模型).如果存在一个聚类模型,在视角l上满足条件或,则该模型被称为视角l上的有效(non-invalid)聚类模型.

定义2(非完美聚类模型).如果存在一个聚类模型,在视角l上并没有完成100%的代表点识别率,则称该模型为非完美(non-perfect)聚类模型.

定义3(条件独立聚类模型).对于视角l的聚类模型ml和视角l⊕1的聚类模型ml⊕1,如果满足以下条件:

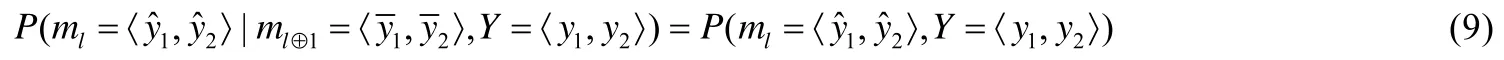
则称ml和ml⊕1是两个条件独立的聚类模型.其中,.这里需要注意的是,我们使用代表点识别率来表示一个聚类模型在某一个视角上的聚类结果.这是因为在基于代表点的聚类模型中,无论是基于单代表点,还是多代表点,如果代表点或代表点的权重系数确定,那么数据的最终划分(标签)也能确定.通过上述 3个定义,我们给出定理1及其证明.

定理 1.如果条件独立的假设能够满足,那么代表点差异性P(ml≠ml⊕1)是有效聚类模型和非完美聚类模型在视角l上代表点识别误差的严格上限.

证明:聚类模型ml的代表点识别误差可以表示为

聚类模型ml和ml⊕1之间的代表点差异性P(ml≠ml⊕1)可以表示为

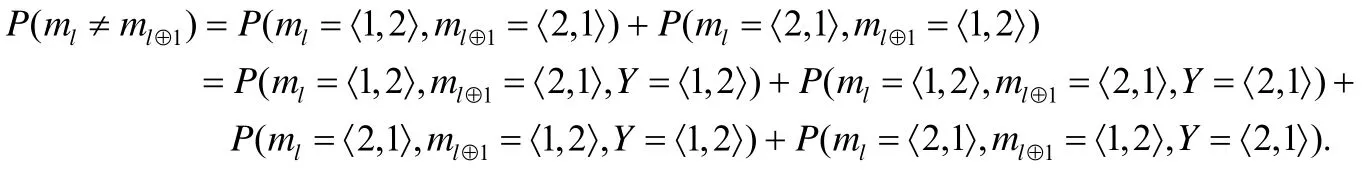
因此,为了证明P(ml≠Y)＜P(ml≠ml⊕1),我们只需证明公式(10)所示的不等式成立即可.

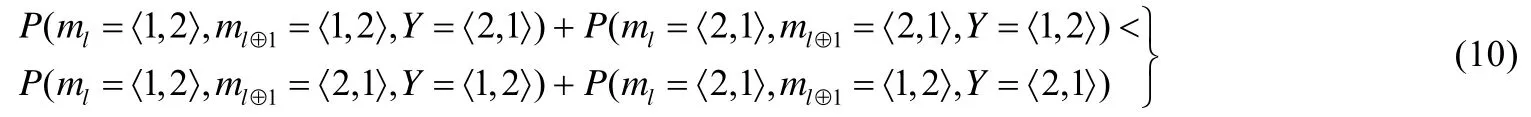
根据定义3和贝叶斯原理,公式(10)可以改写成公式(11)所呈现的形式:

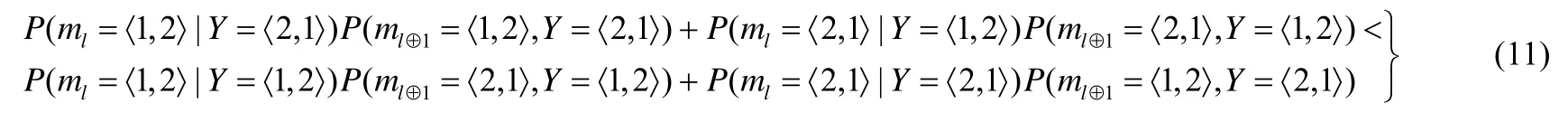
根据定义1和定义2可知:

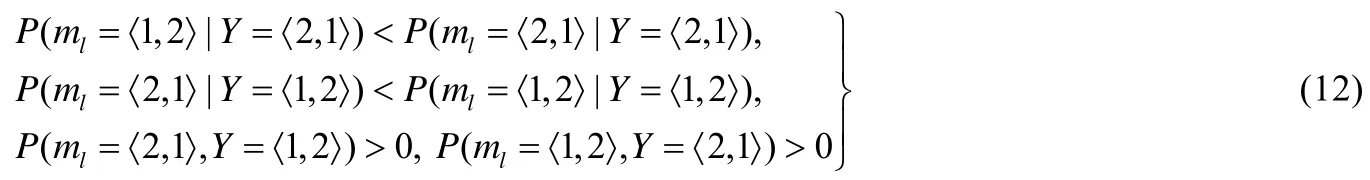
对于任一样本xj,其在视角l下,在簇c中的权重系数为θcj,l,因此,可以采用进行度量,即.换言之,可以反映.因此,根据定理 1,公式(8)所描述的最大化视角间代表点一致性可以降低聚类模型在视角上的聚类误差.

2 MFCMddI算法

2.1 目标函数及其优化策略

将公式(2)和公式(8)带入公式(1),即可得到 MFCMddI算法的目标函数,如公式(13)所示,其约束条件和公式(2)的约束条件相同:

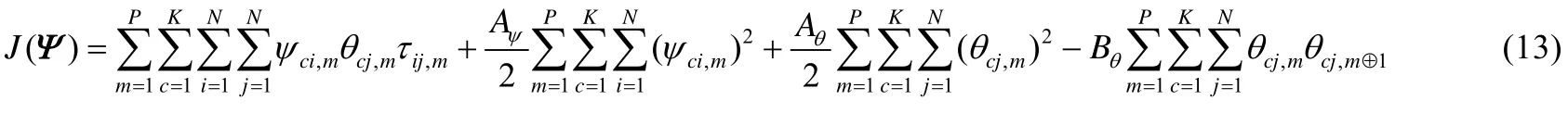
优化公式(13)所示的目标函数可以看成求解一个约束优化问题,通过引入拉格朗日乘子和 KKT条件,可以得到公式(14)所表示的优化目标函数:

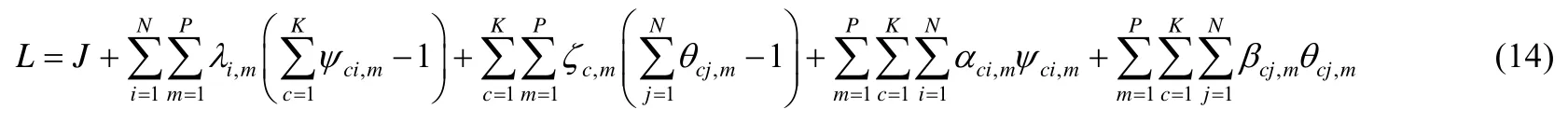
定理2.在给定视角m下的样本权重系数矩阵Θm,公式(14)所呈现的优化目标函数取得极值时需要满足的必要条件为

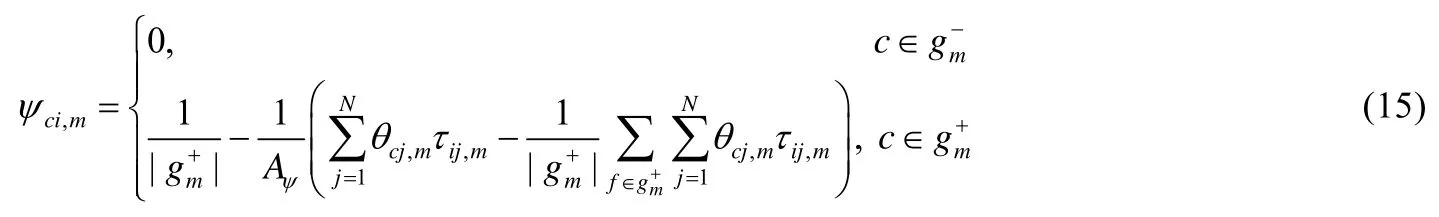
证明:KKT条件如公式(17)～公式(19)所示.

将公式(17)和公式(3)所示的约束条件联合,可以求出:

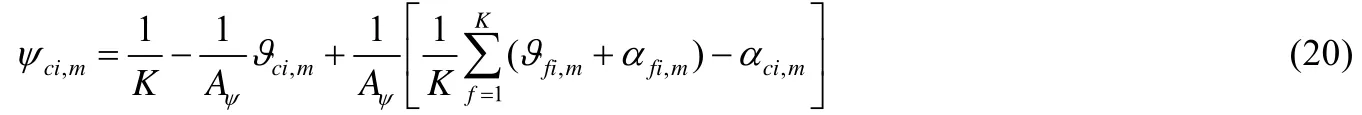
其中,

对于公式(18),可以从以下两个方面进行考虑.

(i)当αci,m=0时,公式(20)可以化简为

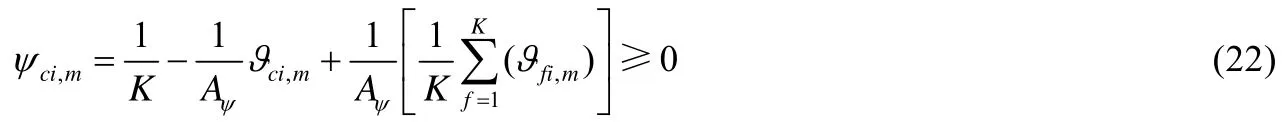
(ii)根据公式(19)所示的 KKT 条件,当αci,m＞0 时,ψci,m=0;当ψci,m＞0 时,αci,m=0.因此,根据约束条件(4),可将簇集合分成两个子集,如公式(16)所示.故对于;当时,,此时αci,m=0.因此,公式(20)可以重写为

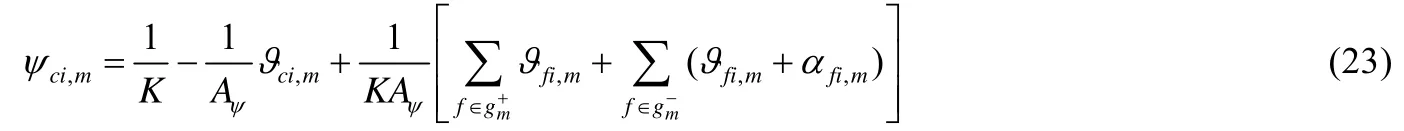
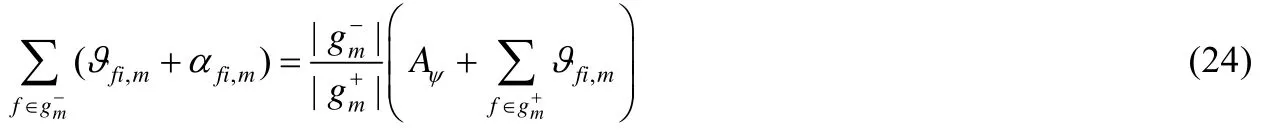
定理3.在给定视角m下的样本模糊隶属度矩阵Ψm,公式(14)所呈现的优化目标函数取得极值时需要满足的必要条件为

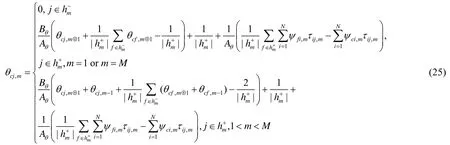
证明:定理3的证明方法与定理2基本相同,需要值得注意的是:公式(14)在对θcj,m求偏导数时,要分m=1和m≠1两种情况分别讨论,证明过程略. □

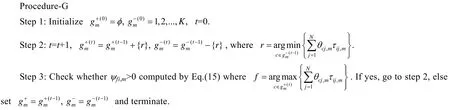
2.2 算法流程和复杂度分析

MFCMddI算法采用ψci,m和θcj,m相互迭代的方式来优化目标函数,即固定一个变量,求解另外一个.这里,我们先初始化ψci,m,然后求解θcj,m.另外,各个视角间存在协同学习(从公式(25)亦可看出,在求解θcj,m时,依赖其他视角的代表点权重系数),因此在算法执行之前,除了需要对ψci,m初始化之外,还需要对θcj,m进行初始化.在文献[22]中,为了避免目标函数陷于局部最优,所采用的初始化策略能够使得簇中代表点在样本空间的分布比较均匀.具体来说,第 1个簇中代表点选自距离其他样本距离之和最小的样本,剩下的簇中代表点选自距离已选代表点最远的样本.因此,MFCMddI算法借鉴这种初始化策略,首先对第 1个视角的ψci,m和θcj,m(m=1)进行初始化,如果在视角1下簇c的中心是xi,则ψci,m=1;否则,ψci,m=0.同样地,如果在视角 1下簇c的中心是xj,则θcj,m=1;否则,θcj,m=0.对于多视角数据而言,由于不同视角之间样本的对应关系是已知的,故在第 1个视角初始化完成之后,其他视角直接采用第 1个视角的结果.这样做的目的是使得在多视角协同聚类过程中,同一个簇在不同的视角下保持一致的标签编号.当算法收敛时,可以获取到每个视角下的模糊划分矩阵.一般来说,可以通过计算其几何均值来获取全局的模糊划分,本文亦采取同样的集成策略,即

其中,Ψm表示视角m的模糊划分矩阵,Ψ表示全局模糊划分矩阵.初始化算法和MFCMddI算法描述如算法1和算法2所示.

算法1.Initialization.

输入:第1个视角样本的距离矩阵Γ1、簇个数K、视角数P.

输出:每个视角的初始模糊隶属度矩阵Ψm和代表点权重系数矩阵Θm;m=1,2,3,…,P.

过程:

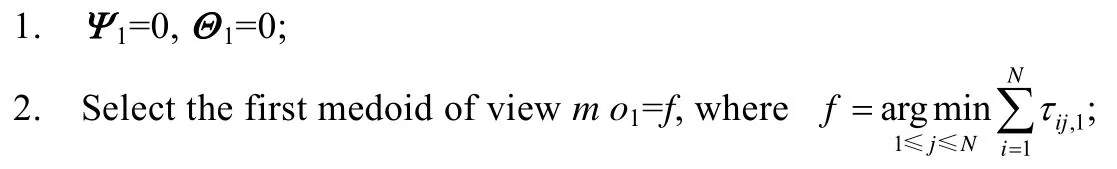
算法2.MFCMddI.

输入:每个视角的距离矩阵Γm(m=1,2,3,…,P);簇个数K;视角数P;平衡参数Aψ,Aθ,Bθ;迭代停止误差ε;m=1,2,3,…,P;初始化得到的各个视角初始的Ψm和Θm.

输出:全局模糊隶属度矩阵Ψ.

过程:

在MFCMddI算法执行之前,需要设置不同的参数,K和ε可由用户按照样本的特征设定,Aψ和Aθ用于控制目标函数中两个泛化项的贡献,Bθ用于控制视角间代表点一致性约束的贡献.为了使各项之间趋于平衡,在Aψ已知的情况下,我们给出另外两个平衡参数的取值指导规则:Aθ=AψN/K,Bθ=Aθ/2.

从算法2的描述中可以看出,MFCMddI算法的时间复杂度由两部分构成,分别为计算每个视角下样本之间的距离所消耗的时间以及迭代过程所消耗的时间.计算样本之间距离的时间复杂度为O(N2P),迭代过程的时间复杂度为O(PNK),因此,整种算法的时间复杂度为O(N2P+PNK),其中,P表示视角数,N表示样本数,K表示簇个数.

3 实验与分析

3.1 实验设置

为了评价 MFCMddI算法在多视角数据集上的聚类效果,本节将在不同类型的数据集上进行实验,包括:(1)人造数据集;(2)真实数据集.另外,还将所提出的算法应用到脑磁共振图像组织分割的场景中.为了突出所提算法的优势,选择相关的单视角聚类算法 FCMdd[22]和多视角聚类算法 MVFCMddV[23]、TW-k-means[16]、CoTrainSpec[11]、Co-FKM[10]、WV-Co-FCM[12]、MFCMdd-RWG-P[24]作为对比算法,并利用指标 NMI(normalized mutual information)[25]和ARI(adjusted rand index)[26]进行聚类效果的评价,其中,NMI基于信息论,ARI基于样本对计数,二者的定义如下.

假设某一数据集包含N个样本,Nij表示由聚类算法产生的第i个簇与真实的第j个簇的契合程度,Ni和Nj分别表示所述第i个簇与第j个簇的样本数,则

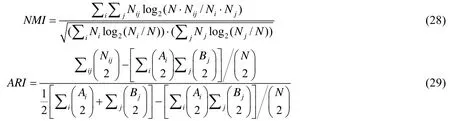
在对脑磁共振图像进行组织分割时,我们采用DC(dice coefficient)和JS(jaccard similarity)来评价分割的效果[27].假设Ai和Bi分别表示算法分割的第i个簇和真实第i个簇,则DC和JS的定义如下:

其中,C表示簇个数,|·|表示集合中元素的个数.DC和JS的取值区间均为[0,1],值越大,表示聚类效果越好.

在实验部分,MFCMddI算法与对比算法的可调参数设置,采用网格搜索策略,并结合评价指标,进行参数寻优,各算法的寻优范围和设置策略见表1.

Table 1 Parameters setup for MFCMddI and comparison approaches表1 MFCMddI和对比算法的参数设置

对于所有的算法实验,分别记录50次独立实验结果的各评价指标的平均值和标准差用于算法性能评价.实验运行的平台为Windows 7,CPU为I5-4950,4核心,内存为8G,MATLAB版本为R2012b.

3.2 人造数据集实验

为了验证MFCMddI算法在视角内的划分质量以及视角间代表点一致性约束的效果,首先构建如图1所示的人工数据集DS1.DS1包含2个视角,每个视角均包含共11个样本,其中,样本1～样本4属于同一簇,其余样本属于另外一簇.由第1.2节所提出的聚类模型可知,当Bθ=0时,MFCMddI退化成基于多代表点的单视角算法.因此,为了验证MFCMddI在视角内刻画簇结构上的优势,选择视角-1,并引入单代表点单视角聚类算法FCMdd,与其在视角内进行聚类效果比较.表2给出了FCMdd和MFCMddI在视角-1上的聚类结果.

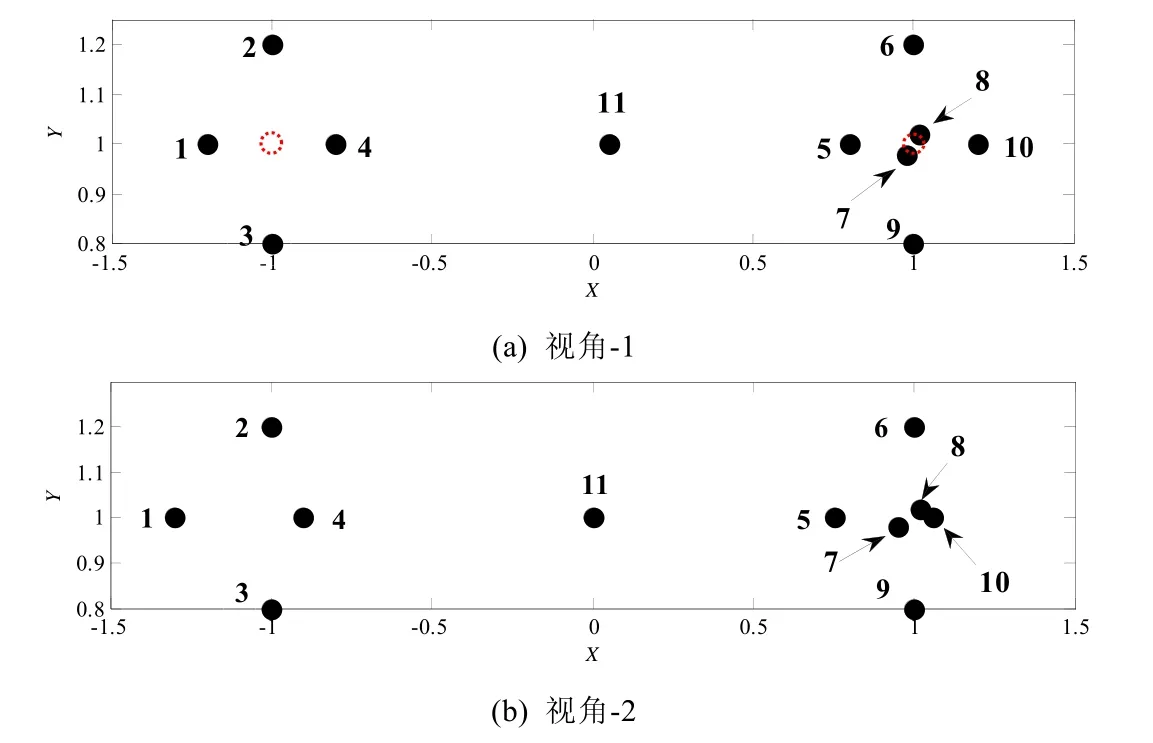
Fig.1 Sample distribution of DS1图1 DS1的样本分布

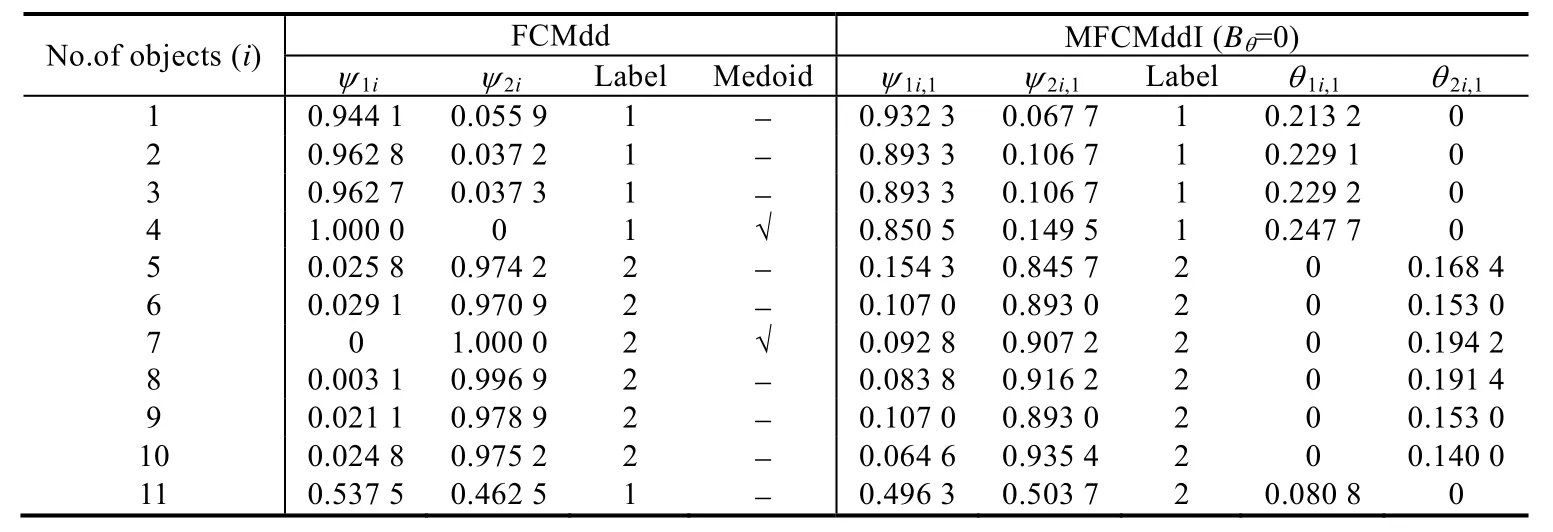
Table 2 Clustering results for FCMdd and MFCMddI on view-1表2 FCMdd和MFCMddI在视角-1上的聚类结果

从表2中可以看出,FCMdd将样本1～样本4、样本11划分为一类,标记成簇1;其余样本划分为另一类,标记成簇2;且算法识别出簇1的代表点为样本4(代表点用“√”标记,非代表点用“-”标记),簇2的代表点为样本7.另外,通过仔细观察亦可发现,在 FCMdd中,代表点隶属于其所代表簇的程度为 1,即ψ24=1.这种现象在MFCMddI中并不存在,在MFCMddI中,并不要求具有最大θ的样本同样具有最大的ψ,例如在簇1中,样本4代表簇1的程度最高,然而其属于簇1的程度低于样本1～样本3.上述现象出现的原因可以归结为如下几点.

1)在FCMdd中,代表点距离自身的距离总为0,按照FCMdd中模糊隶属度的计算方法,其模糊隶属度显然为1.换言之,在FCMdd中,若一个样本被选为一个簇的代表点,那么它不可能再属于其他簇.

2)与FCMdd不同,在MFCMddI进行视角内划分时,不再单独地选择某一个样本作为簇的代表点,而是将所有的样本都当成潜在的代表点,为每一个样本分配不同的权重系数来反映其在簇中的重要程度,从而实现共同刻画簇结构.在某一簇中权重系数高的样本有可能属于另外一个簇.

通过观察样本11的划分情况,亦能发现单代表点和多代表点的区别.在图1(a)中,虚线标识的空心圆代表簇1和簇2的理想簇中心(并非实际样本),从图中可以看出,样本11离右边的簇中心更近,但是从FCMdd划分的结果来看,样本11被划分至左边的簇,因为样本11离代表点4更近,按照FCMdd中模糊隶属度的计算方法,样本11属于簇1的模糊隶属度大于属于簇2的模糊隶属度.这说明,单代表点在刻画簇结构时存在一定的缺陷,尤其是像簇1中无样本靠近理想簇中心时,这种单代表点策略的问题暴露的越明显.但是在MFCMddI,样本11被正确地划分到簇1,这说明多代表点策略比单代表点策略更能刻画簇的结构.

另外,为了观察MFCMddI算法在利用视角间代表点一致性约束进行多视角协同聚类与独立聚类之间的差异,在DS1上分别以Bθ=0以及Bθ≠0两种情况来执行MFCMddI算法,聚类结果见表3.

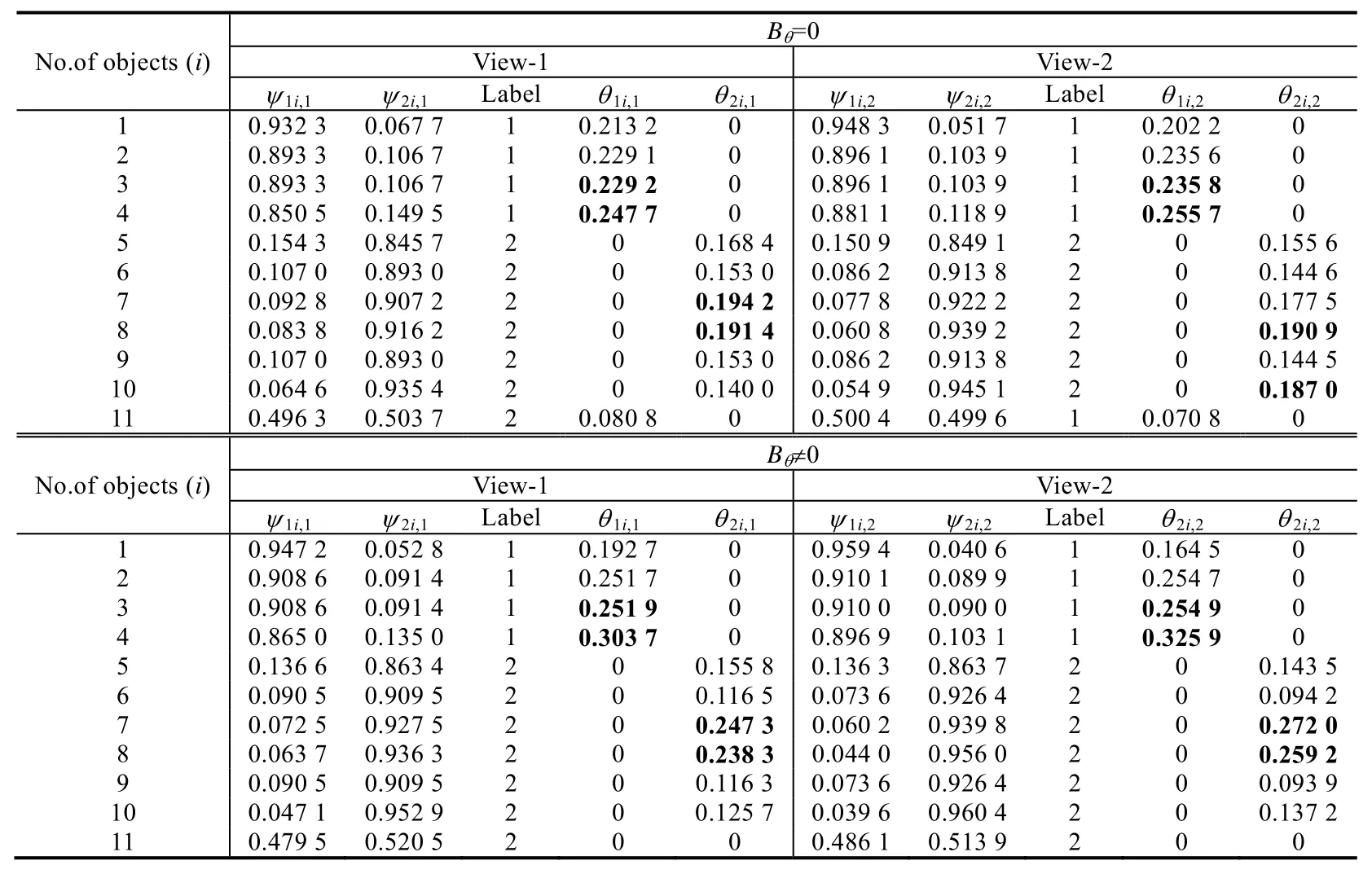
Table 3 Independent and cooperative clustering results for MFCMddI on DS1表3 MFCMddI在DS1上的独立聚类和协同聚类结果

在表3中,加粗的权重系数表示簇中最具代表性的两个样本.从实验结果可以看出,当Bθ=0时,视角-1中簇2的两个最具代表性的样本依次是 7,8,而视角-2中簇 2的两个最具代表性的样本依次是 8,10,即在视角-1与视角-2间,簇2的代表点不完全一致.另外,在视角-2中,样本11被错误地划分至簇1中.当Bθ≠0时,两个视角进行协同聚类,协同的目标是使得视角间对应样本的权重系数乘积之和达到最大,即保持视角间簇中样本的代表性保持不变.从表3的实验结果可以看出,视角-1中簇2的两个最具代表性的样本依次为7,8,视角-2中簇2的两个最具代表性的样本同样依次为7,8.这说明相对于独立聚类而言,MFCMddI算法利用视角间代表点一致性约束,调整了两个视角中样本的权重系数,使得视角间簇中对应样本的代表性保持一致.这一调整使得视角-2中簇 2中样本的代表性变得更为合理,从而使得样本11被正确地划分至簇2中.

为了更进一步地突出MFCMddI算法的多视角协同聚类效果,构建DS2,并引入其他多视角聚类算法进行聚类效果的比较.DS2数据集包含3个视角,由3维空间样本通过向3个2维空间(x-y,y-z,x-z)投影得到,每个视角均包含3个簇共600个样本,如图2所示.

MFCMddI算法以及所引入的对比算法的聚类结果见表4.对于MFCMddI,分别给出在Bθ=0和Bθ≠0时每个视角的聚类结果,当Bθ≠0时,global表示利用公式(27)而得到的全局聚类结果.从表4中评价指标反映的情况来看,在视角-y-z上,相对于独立聚类,协同聚类使得该视角的划分质量有了明显的提升.这一优势可通过图3进一步说明.

Fig.2 Distribution of DS2图2 DS2的样本分布

Table 4 Clustering results in terms of NMI and ARI of different approaches on DS2表4 不同算法在DS2上以NMI和ARI为指标的聚类结果

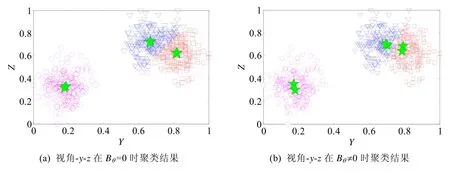
Fig.3 Clustering results of view-y-zwithBθ=0 andBθ≠0图3 视角-y-z在Bθ=0与Bθ≠0时的聚类结果

图3展示了视角-y-z在Bθ=0以及Bθ≠0时的聚类结果.在该图中,按照样本权重系数大小,每个簇中标记了两个最具代表性的点,并用“五角星”表示.对比图3(b)和图3(a)可以看出,在簇中代表点一致性约束的作用下,“▽”表示的簇的两个代表点发生了较为明显的漂移,结合图2(c),我们可以看出,这种漂移是朝着真实簇中心方向,从而使得图3(b)的划分结果更接近真实情况.

对于引入的多视角对比算法,WV-Co-FCM、MFCMdd-RWG-P、TW-k-means和CoRegSpec在DS2数据集上均达到了完美划分,MVFCMddV和Co-FKM表现略差.其原因可以归结为以下几个方面.

1)WV-Co-FCM和TW-k-means算法通过引入香农熵来自适应协同学习不同视角的权重,而对于DS2数据集,视角-x-y具有非常清晰的簇结构边界,因此,这两种算法能够在该视角上学习到较高的权重,使得整个数据集的划分结果极大地偏向于视角-x-y,故取得了表4所示的完美结果.

2)在 MFCMdd-RWG-P算法中,用户可以自定义每个簇中代表点的个数,且强制每个簇在不同的视角下代表点必须一致,同时为每个视角分配权重,权重可以通过与模糊隶属度不断交替迭代,使得目标函数值最小的方式而自适应获得.与WV-Co-FCM和TW-k-means类似,在DS2数据上,由于视角-x-y的易分性,该算法达到完美划分.

3)在CoRegSpec算法中,Kumar等人将半监督学习中的协同正则化(co-regularization)技术移植至无监督学习中来解决多视角聚类问题,并以此构建了多视角谱聚类的学习框架.在该架构中,协同正则化项引入的基础是认为同一样本在不同视角下应该属于同一个簇;另外,对于每个正则化项,可由用户设定正则化参数来控制其贡献;同时,该参数也反映视角的重要程度.因此在 DS2中,由于视角-x-y的易分性,可以通过为该视角分配较大的正则化参数来保证整个数据集的聚类效果.

4)MVFCMddV事实上是FCMdd算法的多视角版本,MVFCMddV针对每个视角,构建样本到簇中心距离矩阵,同时自适应学习每个簇在每个视角下的权重,然后通过加权求和的方式合并各个视角下的距离矩阵,使得目标函数的形式和FCMdd统一.然而,MVFCMddV算法并没有像WV-Co-FCM和TW-kmeans那样考虑视角本身的权重,因而在DS2数据上,视角-x-y易分性所带来的好处并没有得到很好的体现.

5)Co-FKM算法是在FCM的框架下,通过引入模糊隶属度约束项,使得各个视角之间的划分尽量趋于一致.这种协同学习的方式会使得最终的划分结果趋于一种均衡状态,例如,对于 DS2数据集来说会降低视角-x-y的划分质量,但是会提高视角-y-z的划分质量.因此,对于多视角数据集而言,若某个视角存在清晰的簇结构边界,Co-FKM算法并非首选,基于视角加权的算法更加合适.然而对于本文所提出的MFCMddI算法而言,和Co-FKM一样,并没有考虑视角的权重;但是与Co-FKM不同的是,簇中代表点的一致性约束对于原本有着较好簇结构边界的视角(模糊隶属度矩阵偏“硬(crisp)”)不会造成很大的影响,因此在利用公式(27)进行模糊隶属度矩阵合成时,最终的结果会偏向具有较好簇结构边界的视角.这也是MFCMddI算法在未考虑视角权重的情况下,在DS2上取得完美划分的原因.

3.3 真实数据集

为了更进一步地验证MFCMddI算法在真实数据集上的表现,我们从BSDS300中选择一幅大小为121×81的彩色图像(DS3)进行图像分割实验[29],分别将其RBG颜色空间的3个分量当成3个视角,该图像如图4所示,图4(a)为原图像;图4(b)为人工分割结果,作为评价依据;图4(c)为视角-R;图4(d)为视角-G;图4(e)为视角-B.

MFCMddI算法以及所选对比算法在NMI和ARI上的评价结果见表5.另外,图5也给出了从视觉角度的划分结果.从定量评价的结果以及分割视角效果来看,MFCMddI相对于所选的对比算法而言具有一定的优势.

除了DS3之外,我们还使用CMU PIE数据集来测试算法的性能.该数据集包含41 368幅64×64人脸图像,这些图像分别由68人在不同的光照、姿势和表情下获得[30].图6给出了C05和C27组中的示例样本,其中,C05和C07为Deng等人[31]公开的在不同角度和光照条件下拍摄的照片.我们从C05和C27中各抽取100幅图像,构建2视角数据集DS4来进行算法测试,实验结果见表6.

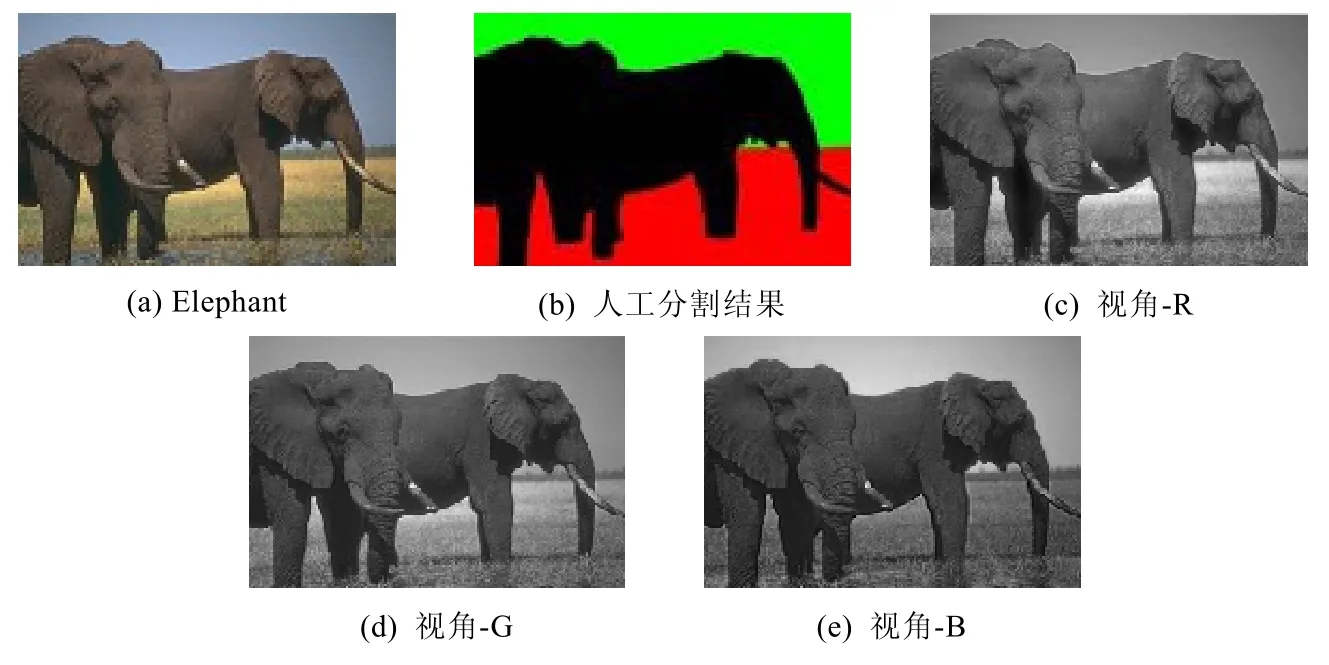
Fig.4 Image elephant,manual partition result and its three views图4 Elephant、人工分割结果及其3个视角

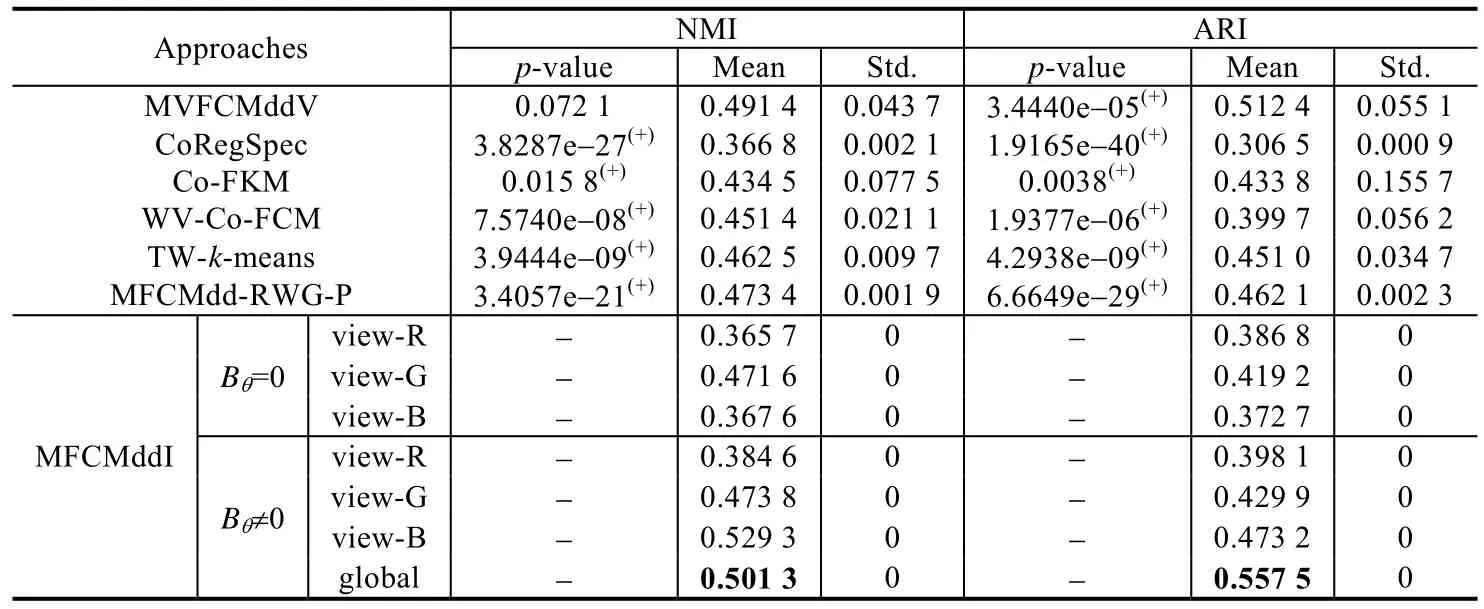
Table 5 Clustering results in terms of NMI and ARI of different approaches on DS3表5 不同算法在DS3上以NMI和ARI为指标的聚类结果

Fig.5 Segmentation results of different approaches on DS3图5 不同算法在DS3上的分割结果

Fig.6 Samples from CMU PIE face dataset图6 CMU PIE人脸数据库中的示例样本

Table 6 Clustering results in terms of NMI and ARI of different approaches on DS4表6 不同算法在DS4上以NMI和ARI为指标的聚类结果

从表6中可以看出,相对于所引入的对比算法,MFCMddI在评价指标NMI和ARI上取得了最佳的表现效果.相对于对比算法中表现最好的WV-Co-FCM,NMI指标提升了6.69%,ARI指标提升了9.83%.相对于表现最差的MFCMdd-RWG-P,NMI指标提升了18.54%,ARI指标提升了32.2%.另外,图7给出了在协同状态以及非协同状态下,MFCMddI算法在 DS4上的可视化聚类结果以及代表点选择情况(每个簇标注了两个最具代表性样本,且标注中的数字表示样本在原始数据集中的编号).

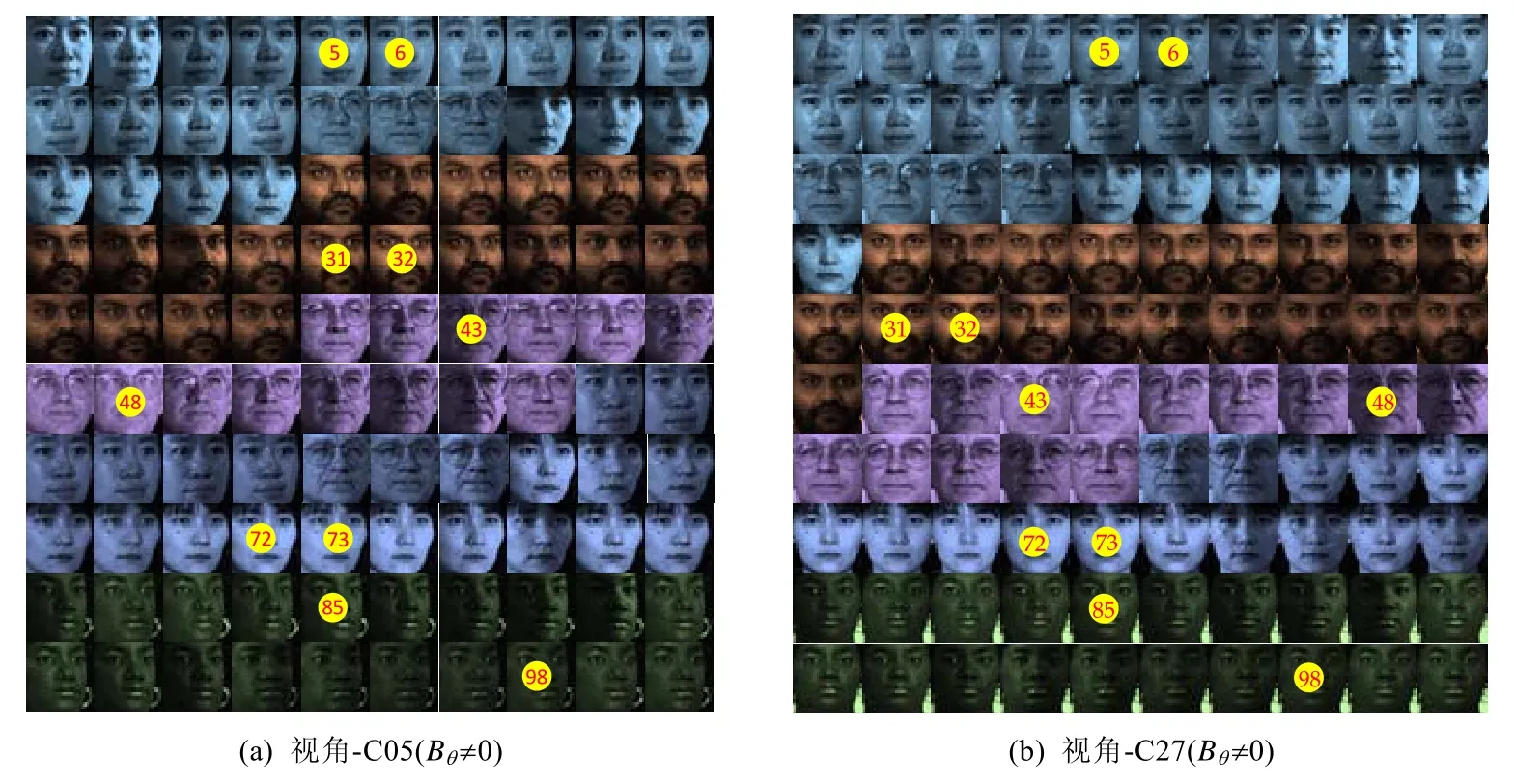
Fig.7 Clustering results of MFCMddI on each view of DS4 withBθ≠0 andBθ=0 respectively图7 在Bθ≠0和Bθ=0时MFCMddI算法在DS4上各个视角聚类结果

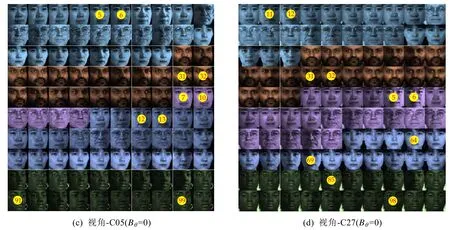
Fig.7 Clustering results of MFCMddI on each view of DS4 withBθ≠0 andBθ=0 respectively(Continued)图7 在Bθ≠0和Bθ=0时MFCMddI算法在DS4上各个视角聚类结果(续)

从图7中可以看出,在非协同状态,视角-C05与视角-C27所标记的代表样本在大多数情况下并不相同.然而在DS4中,两个视角的样本是同一个志愿者在不同角度和光照条件下获得,故在DS4中,往往存在这样的一个事实:在视角C05中具有代表性的样本在视角C27中仍然具有代表性.所以,利用这样的事实作为约束条件进行视角间协同聚类,能够改善非协同聚类的性能.而从表6的定量分析以及从图7所呈现的视觉效果来说,确实如此.

从在DS3和DS4这两个真实数据集的实验结果来看,基于视角加权策略协同聚类的算法,如WV-Co-FCM、TW-k-means、MFCMdd-RWG-S并未像在DS2上一样取得最佳的划分结果.这是因为在DS3和DS4上,任一视角上都不具备存在明显的簇结构边界的优势,这使得这类聚类算法所学习的权重的差异不够显著.然后,这两个数据集在各个视角上却能保持如前所述的事实,即样本的重要程度在各个视角间差异很小,这样的事实却是有利于所提出MFCMddI算法的学习,因而在两个数据集上取得了具有一定竞争力的划分结果.

3.4 应用案例

从脑部磁共振图像(magnetic resonance images,简称 MRIs)中分离出脑组织,包括灰质(gray matter,简称GM)、白质(white matter,简称WM)和脑脊液(cerebrospinal fluid,简称CSF)对于临床诊断和辅助决策有着非常重要的作用[32-34].我们从McGill大学MN(McConnel brain imaging center of the montreal neurological institute)协会提供的BrainWeb模拟数据库[35]中选择5幅脑部磁共振图像,相关属性见表7.

Table 7 Properties of selected MRIs表7 所选脑部核磁共振图像的相关属性

ID为1的MRI及其解剖学上的分割结果(作为金标准)如图8所示.对于所选的5幅MRI,分别利用Gabor滤波器抽[36]取不同的特征构建3个不同的特征视角,然后在所构建的多视角数据集上执行MFCMddI算法和对比算法,并利用JS和DC指标进行评价.表8给出了所有算法在5幅MRI上运行的均值和标准差(每幅图像独立执行 50次,获得均值和标准差,然后再取每幅图像的均值的平均值和标准差的平均值).对于 MFCMddI,仅给出集成后的全局划分结果.从表8的结果来看,TW-k-means和MFCMddI均取得了较好的分割效果.

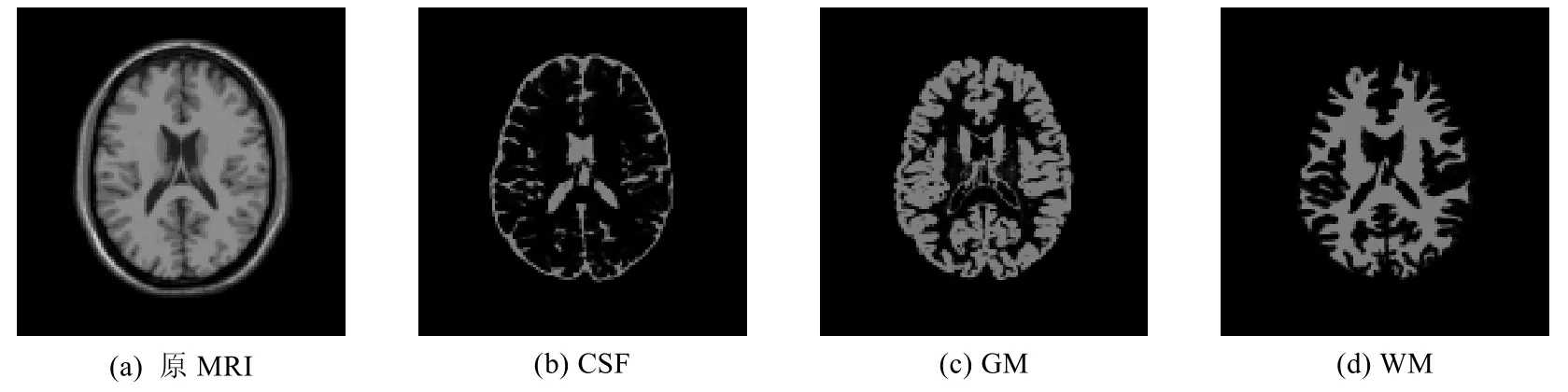
Fig.8 Illustration sample of MRI and anatomical segmentation resutls图8 MRI示例样本和解剖学分割结果

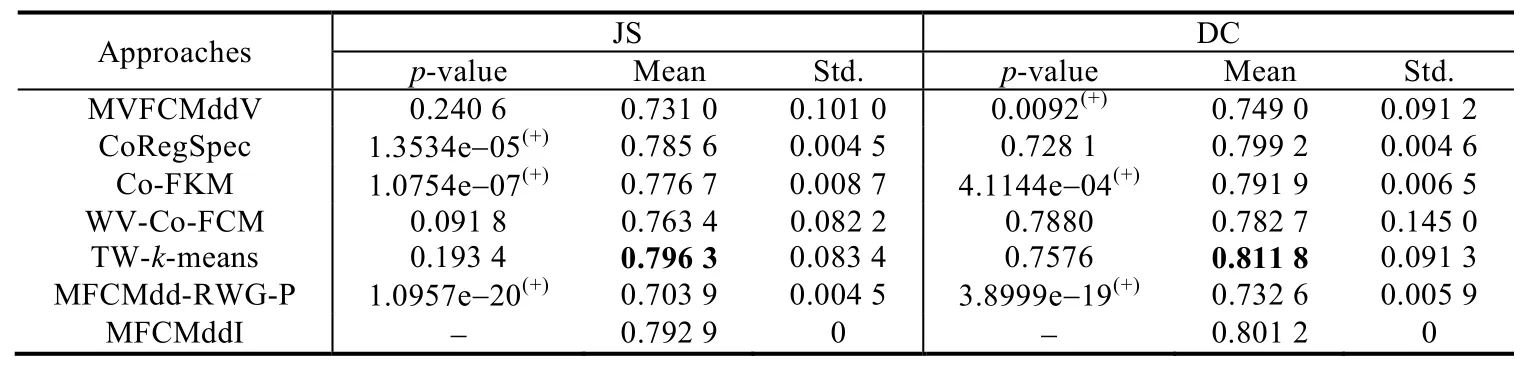
Table 8 Clustering results in terms of JS and DC of different approaches on MRIs表8 不同算法在MRI上以JS和DC为指标的聚类结果

3.5 参数分析

MFCMddI算法中,需要分析的主要参数有Aψ,Aθ,Bθ,其中,Aθ与Bθ可按照前文所述的指导规则设定.故只需分析Aψ在不同取值下对MFCMddI算法聚类效果的影响.我们从0.001～3这个区间中,为Aψ设定14个不同的值,分别为0.001,0.005,0.01,0.06,0.09,0.14,0.20,0.25,0.3,0.7,1,1.5,2和3,然后从NMI和ARI中选择一个评价指标(这里选择NMI,ARI类似),在DS2、DS3和DS4上评价MFCMddI算法在不同Aψ下的聚类效果,从而分析算法对参数Aψ的敏感性.图9给出了MFCMddI算法在所选3个数据集上,评价指标NMI随Aψ变化的曲线.

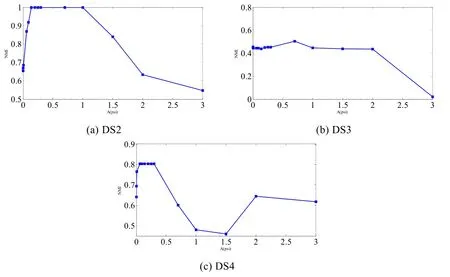
Fig.9 Clustering results on DS2,DS3 and DS4 in terms of NMI for the proposed MFCMddI with different parameterAψ图9 MFCMddI算法在DS2、DS3和DS4上NMI随参数Aψ的变化关系

从图9中可以看出,参数Aψ对MFCMddI算法的聚类效果有着较大的影响,较大或者较小的取值都会降低算法的性能,在实践中,可以在[0.001,0.8]中进行参数寻优.

4 结 论

传统的单视角聚类算法在应用于多视角聚类任务时缺乏有效的协同学习方法.针对此问题,本文首先提出了一种多视角聚类模型.该模型的目标函数由两项构成:第1项反映视角内划分质量;第2项为约束项,反映视角间的协同学习机制.在此基础上,提出了一种基于多代表点一致性约束的多视角模糊聚类算法.该算法通过采用簇结构多代表点表示策略来保障视角内的划分质量;同时,认为簇内代表点在不同的视角下能够保持其代表性,进而在算法的目标函数中,通过最大化两两相邻视角下代表点权重系数的乘积之和的方式进行协同学习.理论分析表明,该协同学习机制确实能够保证聚类效果的提升.最后,在人工数据集以及真实数据集上,通过实验验证了该算法在多视角数据集上的聚类效果,并通过与同类算法的对比,突出该算法的优势.

尽管 MFCMddI算法在多视角数据集上具有不错的聚类效果,然而在后续的研究过程中,仍然存在进一步拓展的空间,例如,如何解决不同视角下样本数量不一致问题、如何差异化地对待不同的视角问题等.这些问题也将成为我们后续研究的重要目标.