基于改进的动态Kriging模型的结构可靠度算法

魏娟， 张建国,*， 邱涛

(1. 北京航空航天大学 可靠性与系统工程学院, 北京 100083；2. 北京航空航天大学 可靠性与环境工程技术重点实验室, 北京 100083)

当现有的可靠性分析方法应用于复杂的工程结构时，往往面临巨大的挑战[1]，功能函数通常是高度非线性甚至是隐式的，而且需要借助有限元分析(Finite Element Analysis，FEA)进行评估，计算量大，计算时间长[2-3]。一阶可靠度算法(First Order Reliability Methodology，FORM)、二阶可靠度算法(Second Order Reliability Methodology,SORM)已被广泛用于估算结构系统失效的概率[4]，但是只能适用于功能函数表达式已知的情况。蒙特卡罗模拟(Monte Carlo Simulation,MCS)方法是结构可靠性分析中最简单也是最广泛使用的方法，计算精度高，适用于结构可靠性的隐式问题。但由于工程结构的失效概率通常较小，MCS须生成大量样本以确保准确性，所带来的计算成本可能会变得非常高，从而极大地限制了MCS在工程中的应用。

为了降低可靠性分析的计算成本，代理模型越来越多地被用来实现结构可靠性。代理模型作为一个近似模型可以找到输入和输出之间的潜在关系。如果与功能函数足够接近，则代理模型可以完全表示功能函数，以准确评估性能函数的值。常用的方法有响应面方法(Response Surface Methodology，RSM)[5]、支持向量机[6]、神经网络[7]、Kriging 模型[8]。其中，Kriging模型是一种方差估计最小的无偏估计的随机过程算法，由于其对非线性函数的良好近似能力和独特的误差估计功能[9]，越来越多地用于可靠度的求解过程。Zhang等[10]运用Kriging模型进行结构可靠度分析，Liu等[11]运用Kriging模型和MCS方法进行齿轮接触可靠性的分析。刘瞻[12]和陈志英[13]等将人工智能优化算法融入到Kriging模型的构造中，进一步提高了预测精度。为了降低复杂结构的可靠性分析的计算成本并实现快速可靠性分析，尽可能减少样本数量，Ma等[14]在采样过程中应用学习函数，从而构造Kriging模型，Li等[15]提出一种基于最可能失效点(Most Probable Point,MPP)的局部抽样方法，提高了Kriging的精度。Echard等[16]提出动态Kriging联合MCS的可靠度计算方法。Xia等[17]提出了一种基于自适应动态泰勒Kriging的高效可靠性优化算法。通过二元粒子群算法优化选择基函数，并确定具有期望拟合误差的最小数量的采样数据。

由于初始训练的高质量样本总是难以获得，本文在训练小样本的基础上，采用修改代理模型拟合误差的动态更新机制。针对复杂结构隐式功能函数的可靠性分析问题，本文将混合粒子群-模拟退火(Particle Swarm Optimization-Simulated Annealing,PSOSA)算法应用到动态Kriging模型中相关参数的寻优过程，并将改进的Kriging模型应用于可靠度的分析计算问题。该方法运用PSOSA算法高效求解最优相关参数，构造Kriging模型；同时基于动态更新机制，逐步加入最佳样本点，从而不断修正 Kriging 模型的精度，并结合一次二阶矩法进行可靠度计算。

1 动态Kriging模型

1.1 Kriging模型

近年来,Kriging模型作为一种新型的响应面模型技术在航天等工程优化领域中得到了广泛应用。对于k个n维样本点及其对应的响应值Y=[G(x1),G(x2),…,G(xk)]T，Kriging模型采用高斯随机过程模型，其插值结果定义为已知样本函数响应值的线性加权[9]，即

(1)

式中：x=[x1,x2,…,xk]T；f(x)=[f1(x),f2(x),…,fp(x)]T为回归多项式基函数向量，p为回归多项式的数量；β=[β1,β2,…,βp]T为多项式参数向量；z(x)为服从正态分布N(0,σ2)的随机过程，σ为标准差，协方差方程为

cov(z(xi),z(xj))=σ2R(xi,xj)

i,j=1,2,…,k

(2)

式中：R(xi,xj)为样本点中任意2个输入向量xi和xj的空间相关方程，通常采用高斯相关方程，其形式为

(3)

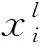
(4)

式中：R为相关矩阵，其中元素Rij=R(xi,xj)(i,j=1,2,…,k)，相关参数直接控制着Kriging模型的输入输出特性。

基于给定的样本点，多项式参数向量β与随机过程方差σ2的估计值计算式分别为

(5)

(6)

式中：F为由回归多项式函数值组成的回归矩阵[18]。

(7)

u=FTR-1r0-f

(8)

(9)

式中：r0=[R(x0,x1),R(x0,x2),…,R(x0,xk)]T。

1.2 动态更新机制

为了提高可靠性分析的效率，动态代理模型应符合以下条件：①初始样本数量小；②用于小样本学习的替代模型拟合；③每迭代一次，对FEA进行一次调用，以修正代理模型。

本文选择动态Kriging模型来减少调用FEA的次数。代理模型的计算精度主要取决于对极限状态面的逼近程度。一般来说，使用一些预设的训练样本很难构建具有高拟合精度的响应曲面，而响应曲面的动态更新可用于校正拟合误差。动态Kriging可靠度具体算法流程如下：

步骤1建立初始的样本集。通过拉丁超立方抽样生成初始样本点，并调用FEA计算其响应值。

步骤2构造动态Kriging。首先，通过优化技术寻找最优相关参数；然后，设置最优基函数，并构造代理模型来近似目标函数。

步骤3利用DACE工具箱可求出模型对各个变量的梯度，结合FORM法计算MPP[12]。判断MPP是否收敛。若是，求解可靠度等指标。若否，进入步骤4。

步骤4上述MPP作为新的样本点加入初始样本集，继续迭代。

上述过程实现了可靠度计算过程中，Kriging模型在实际极限状态响应面附近拟合误差的自适应修正。减少了FEA的调用次数，这使计算成本大大降低，有利于减少模型对样本的依赖程度，加快了收敛速度。

2 改进的动态Kriging模型

2.1 优化算法

2.1.1 PSO算法

(10)

(11)

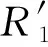
本文中系数w由式(12)确定：

(12)

式中：C=c1+c2。

PSO的工作原理如下：首先，粒子群由搜索区域内随机分布的粒子组成，然后，PSO通过更新粒子的速度和位置来迭代寻找最优解。当满足收敛标准时，循环终止。但是，运用公式Pb和Pg来搜索最优解，收敛速度快。然而所有粒子有移向最优经验点的趋势，并在局部区域内搜索，所以可能会导致收敛过早的问题。因此，尽管PSO比其他方法收敛速度快，但结果可能精度不高。

2.1.2 SA算法

模拟退火算法起源于固体退火原理，模拟了高温金属降温的热力学过程。在搜索过程中具有概率突跳的能力，能够有效地避免搜索过程中陷入局部极小解。试验点从xi到xi+1的接受概率为

(13)

式中：y为目标函数，Δy=y(xi+1)-y(xi)和T为控制参数，可类比为温度，温度的降低实际上控制了接受概率。

设φj为每个变量接受的移动次数与试验次数的比值，则扰动可写为

Xtrial=Xcurrent+R′(-1,1)V

(14)

式中：R′(-1,1)为-1～1之间的随机数；V为步长向量。Vbi是变量上下界之差的一半，可表示为

(15)

式中：Vi为V中的元素。

理论上证明，当采用非常缓慢的温度下降率时，找到全局最小值的概率可以接近1。

最常见的温度下降规律为

Ti+1=RTTi

(16)

式中：T0为初始温度；RT为0.8～0.999 9之间的常数。

2.1.3 混合PSOSA算法

在混合PSOSA算法中，搜索最优解时，速度矢量控制粒子在搜索空间内的移动方式。速度矢量有3部分组成：

本文PSOSA算法的主要思想是通过更新群体的群体最佳位置来改善群体的社会行为。当PSO循环中最优解没有改进时，旧的群体最佳位置将被替换为使用SA算法计算的新位置。新的最佳位置实际上向群体的社会领导者(即前一个全局最优解所属的粒子)发出信号，用于更新其方向。PSOSA算法充分结合了PSO算法全局搜索能力和SA算法的局部搜索能力，能达到很好的收敛结果。算法示意图如图1所示,具体算法如下：

步骤1初始化。m为粒子群粒子的数；imax为允许最大迭代次数；w为权重因子；c1和c2为学习因子；vmax为速度阈值，T0为初始温度；RT为温度降低参数。

步骤2粒子的位置。可行域均匀分布m个粒子；确定每个粒子的适应度值。

步骤4更新每个粒子的速度和位置：

步骤6判断最优解是否有所改进。如果第i+1次迭代的Pg没有优于第i次迭代的Pg，则进入步骤7；否则，更新温度Ti+1=TiRT，返回步骤4。

步骤8重复整个过程直到收敛。

该算法主要有以下几个特点：

1) 通过改进速度矢量的组成促使群体向整体最优位置所在的搜索空间移动，这加快了收敛过程。

2) PSO算法和SA算法的结合提高了整个寻优机制的质量和稳定性。

3)在SA迭代中PSO速度公式中的认知成分得到了保留。

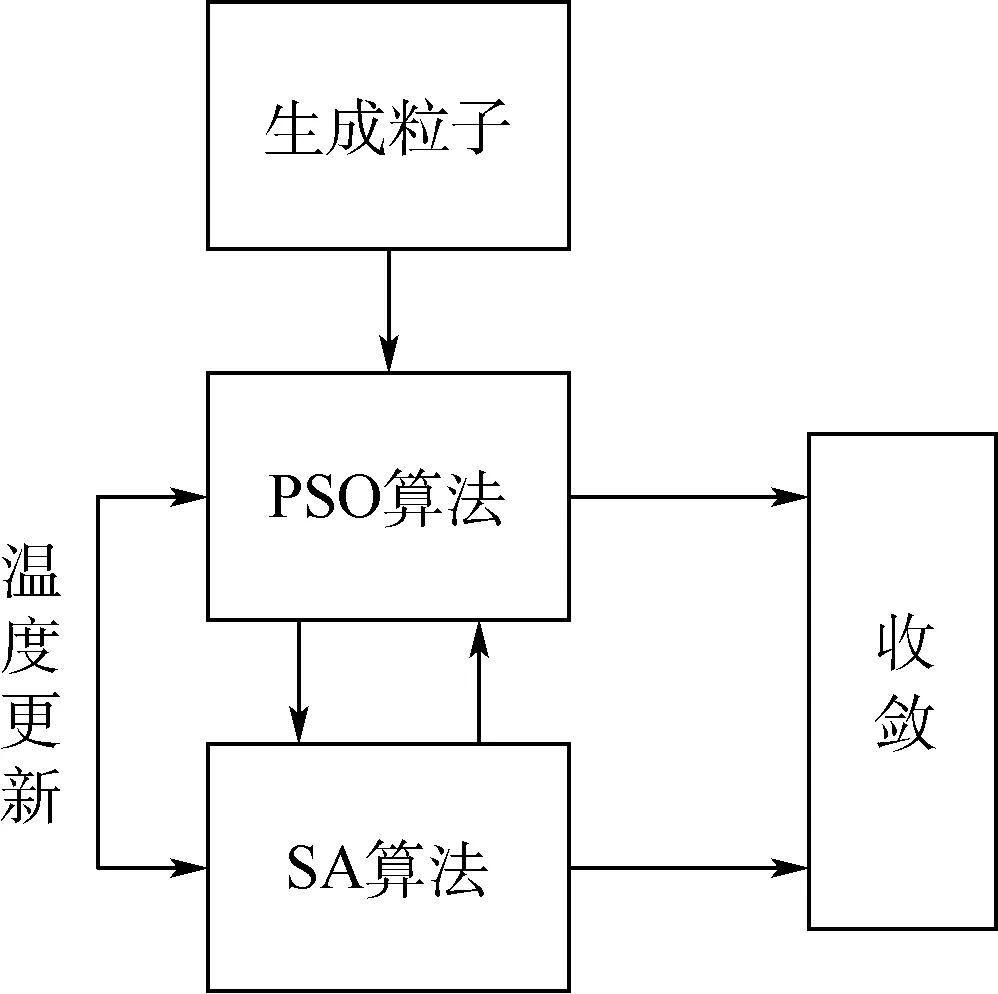
图1 PSOSA算法示意图Fig.1 Sketch map of PSOSA algorithm

2.2 Kriging建模流程

目前Kriging 建模过程普遍采用的模式搜索法对初始点十分敏感，容易造成求解θ*无法收敛，Kriging 预测精度很低。主要原因是模式搜索所采用的单点序列搜索方式决定了它只能从一个指定的起点出发，并收敛于一个距起点较近的局部最优解。为了寻找最优θ*，只能将起点接近于θ*，然而这很难确定。不仅如此，模式搜索法搜索路径单一，不能根据似然函数的变化而变化，因此即使根据经验信息，使起点接近θ*，搜索路径也有可能偏离导致无法收敛[13]。

本文一方面运用PSOSA算法进行搜索，种群中各粒子在搜索最优解的过程中实现信息共享，每个粒子不断根据个体极值与群体极值的变化情况动态调整着自己的搜索方向，另外，当PSO循环没有改善，原来全局最优位置被通过SA计算得到的新位置代替，从而在缺乏先验信息的前提下，也能搜索到最优解θ*。另一方面,通过自适应动态更新机制减少调用FEA的次数，从而提高计算效率。

其中，运用PSOSA算法搜索极大似然意义下的最优相关参数时：

1) 似然函数作为适应度函数。

2) 为转化为无约束优化，粒子采用对数形式。

综上所述，本文的总体计算流程如图2所示。

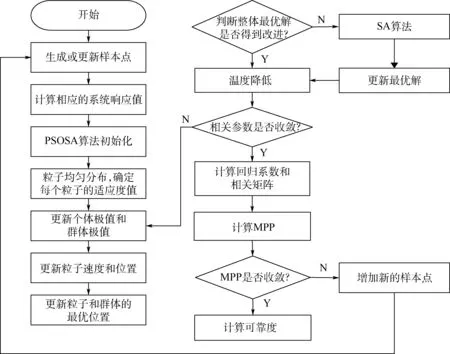
图2 改进的动态Kriging模型流程图Fig.2 Flowchart of improved dynamic Kriging model

3 案例分析

3.1 数值算例1

假设某结构的极限状态函数[12]为

G(x)=x1x2-1500

(19)

式中：x1和x2的分布类型为正态分布，x1～N(38,3.8)，x2～N(54,2.7)，并且x1和x2相互独立，具体分布参数见表1。本案例中，c1=1.5，c2=1.5，RT=0.8，w=2。

表1中，βr为可靠度系数，βr越大，可靠度越大。

对比MCS、RSM、经典Kriging和PSO-Kriging[13]方法，由表1结果可知，MCS方法选取样本点108，计算失效概率结果为6.3×10-3；RSM方法处理非线性问题有一定的局限性，计算结果误差较大；经典Kriging方法、PSO-Kriging方法与本文算法选取同样数量的样本数量，失效概率与MCS方法接近，但是经典Kriging方法与MCS方法相比，误差为4.76%，PSO-Kriging方法误差为4.13%，本文算法误差为1.58%。由此看出本文算法精度相比于其他2种方法有所提高。

将式(19)转化为标准正态分布变量空间下的功能函数，即

G(u1,u2)=Gx(σx1u1+ux1,σx2u2+ux2)=

(σx1u1+μx1)(σx2u2+ux2)-1 500

(20)

式中：u1和u2相互独立，均服从标准正态分布。转换后的极限状态函数G(u1,u2)=0为一曲线，G(u1,u2)>0一侧为安全域，G(u1,u2)<0一侧为失效域，如图3所示。根据本文所提算法，首先在给定随机变量空间内，生成初始设计点，建立Kriging模型，并通过后续的动态更新机制逐渐增加样本点。初始设计点和拟合过程的样本点如图4所示。由图可知，通过更新机制可以有效选择功能函数附近的样本点，可以充分利用少量样本点的信息拟合待求功能函数。

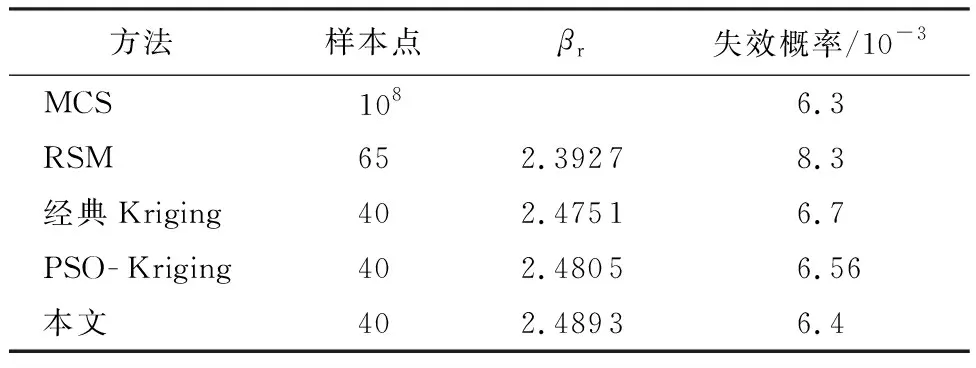
表1 不同方法结果对比(算例1)Table 1 Comparison of results of different methods (Example 1)

图3 极限状态函数Fig.3 Limit state function

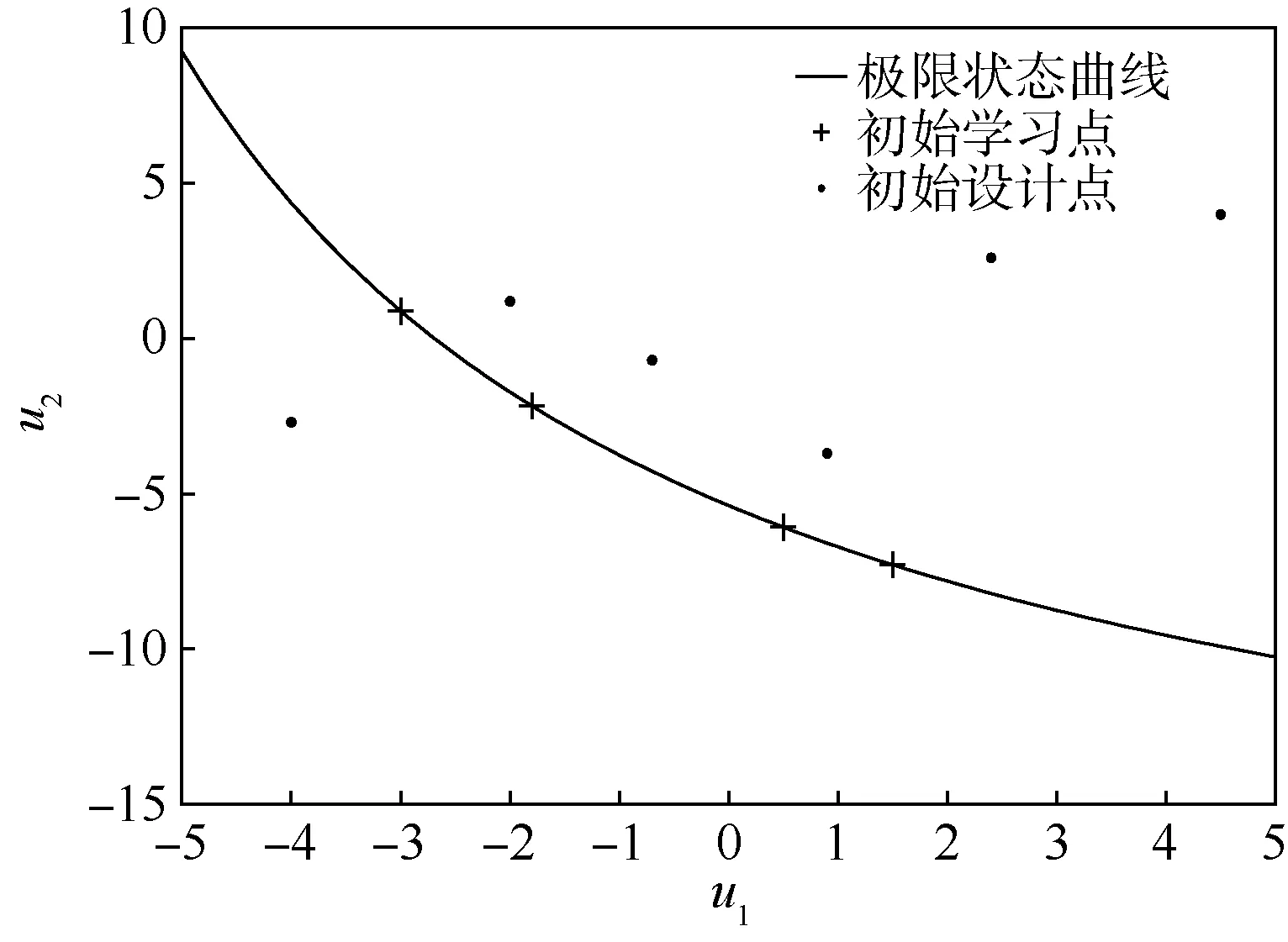
图4 算法说明图Fig.4 Illustration of algorithm

3.2 数值算例2

将本文计算结果与其他方法进行对比，结果如表2所示。表2说明RSM在处理高度非线性问题时无法准确收敛和获得正确结果。与其他方法相比，本文算法的结果与MCS结果最接近。其中MCS计算时间长达60.68 s，本文算法需时12.18 s。

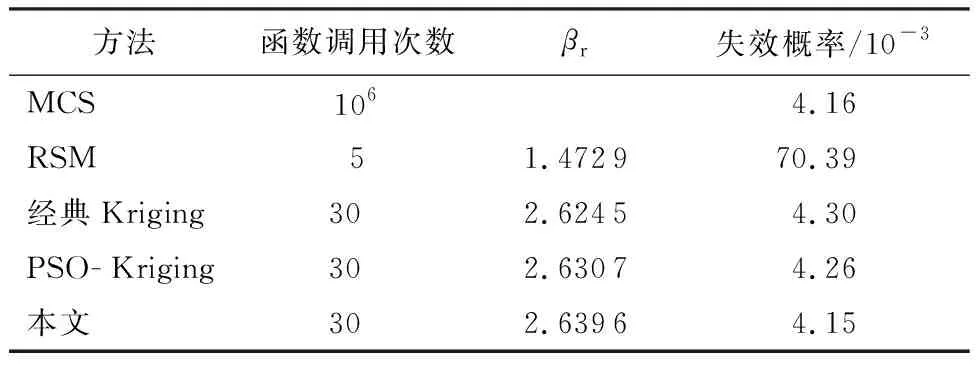
表2 不同方法结果对比(算例2)Table 2 Comparison of results of different methods (Example 2)

3.3 工程案例

涡轮盘是现代航空发动机的核心部件，它在发动机燃烧室内受到高温燃气的推动，将燃气的热能转化为机械能，驱动发动机的运转。其可靠性水平的高低直接影响发动机的技术水平。

本文选择某航空发动机涡轮盘为例，盘上销钉沿周向均匀分布。参数不确定性的主要来源主要包括载荷、材料的随机性。本文取转速均值为9 550 r/min，销轴的材料为3Cr13，轮盘的材料为TC11，叶片的载荷施加在销轴上，合力均值为24 925 N。具体参数信息见表3。

涡轮盘的可靠性水平的高低主要取决于结构危险点处的应力应变分布。由于结构形状、载荷为完全对称的，本文选取轮盘的1/37为研究模型。首先以各变量的均值为设置参数，借助ANSYS 18.1 进行仿真计算，得到结果如图5所示，轮盘与销轴交界处应力应变水平最高，是结构的危险点，其中最大应力为0.834 GPa，最大应变为0.010 17。

当危险点的最大应力超过允许值Rmax=0.97 GPa，则结构发生失效，相应的功能函数可表示为

G=Rmax-S(ω,E1,ε1,ρ1,E2,ε2,ρ2,P)

(21)

上述功能函数为隐式函数。

采用本文所提算法进行可靠度计算，首先建立Kriging模型，其中相关参数θ*的迭代过程见图6。

由图6可以看出，随着迭代次数的增加，本文所提算法在第15次迭代时基本寻得最优相关参数θ*。

利用本文算法与ANSYS 18.1、 Isight进行联合仿真计算，最终求得可靠度。为了验证本文算法的有效性和工程实用性，将其与MCS方法进行对比，结果如表4所示。

表3 涡轮盘参数Table 3 Parameters of turbine disk

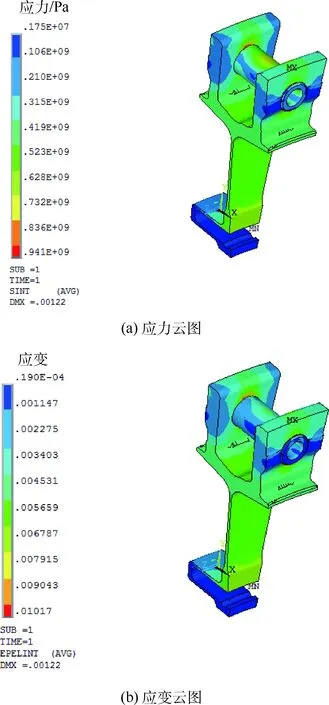
图5 应力和应变计算结果Fig.5 Calculation results of stress and strain

图6 θ*的迭代过程Fig.6 Iteration process of θ*

表4 计算结果对比Table 4 Comparison of calculation results

方法函数调用次数样本点失效概率/10-3MCS方法1053.300本文算法15403.352

由表4可知，本文算法的结果与MCS结果十分接近，误差仅为1.576%，验证了本文算法的有效性以及准确性，并适用于工程实践。

4 结 论

1) 将PSOSA算法引入Kriging的构造过程，PSO算法的全局搜索能力及SA算法跳出局部极小值的能力相结合，克服了经典Kriging过程的局限性和对初始样本点的依赖，保证了极大似然意义下的最优相关参数的求解精度，使寻优过程更加高效和精确，从而有效保证了Kriging模型的预测精度。

2) 本文同时通过动态更新机制，尽可能地减少样本点和调用有限元等数值计算的次数，能够较好地解决功能函数隐式和高度非线性的问题，通过数值案例分析，相比于其他可靠度算法，能够有效提高可靠度计算的效率和精度。通过工程案例分析，本文所提算法可应用于工程实际问题，尤其是功能函数隐式且复杂的问题。有一定的工程实用价值。