弹性高速飞行器的状态/参数滚动时域估计

陈尔康， 荆武兴， 高长生

(哈尔滨工业大学 航天学院, 哈尔滨 150001)

高速飞行器指高速飞行的有翼或无翼飞行器[1]，具有强非线性、不确定性、强耦合等特点[2]。此外由于大量使用轻质材料，其结构的固有频率较低，机体弹性形变对其控制有较大影响[3]，控制系统需要对弹性进行抑制以保证稳定性[1]。现有研究多将弹性振动看作干扰并在控制回路中加以抑制[4]，这样虽然能够保证飞行器的稳定，但难以提高响应速度和控制精度等性能。要实现弹性高速飞行器的精细姿态控制[3]，需要使用动态面控制、模型预测控制等先进控制方法，这势必需要引入难以直接测量的弹性状态的反馈，因此对弹性振动状态进行估计十分重要。除弹性振动状态外，弹性振动的相关参数如弹性模态固有频率等也十分重要，能够用于飞行器的故障诊断等。固有频率与飞行器状态相关，在飞行过程中并非常数，因此对其进行估计是十分必要的。综上，需要研究弹性高速飞行器的状态/参数联合估计方法[5]。

作为一种基于模型的递归滤波器，扩展卡尔曼滤波(EKF)利用一阶线性化的方法对卡尔曼滤波(KF)进行扩展，是当前较为成熟和使用广泛的状态/参数估计方法[5]。虽然EKF可以通过将参数扩展为状态量的方式对参数进行估计，但受限于噪声模型难以估计时变参数；此外，EKF也无法处理状态量的约束[6]。而滚动时域估计(MHE) 方法则从最优控制问题的角度出发[7]，并引入滚动时域策略[8]，通过求解优化问题实现对状态/参数的估计；因此滚动时域估计能够较好地处理带约束的估计问题和状态/参数联合估计问题[5]，近年来得到越来越广泛的应用。文献[9]建立了滚动时域估计渐近稳定和有界稳定的充分条件，并给出了一种算法实现。文献[10]在化学工程问题中利用滚动时域估计进行状态/参数联合估计。文献[11]将滚动时域估计用于航天器的姿态估计和传感器参数校正。文献[12]则研究了机器人的多速率采样滚动时域估计问题。

对滚动时域估计的研究可分为两大类：到达代价的计算和优化问题的求解。到达代价的计算直接关系到滚动时域估计的准确性和稳定性。文献[7]推导了滚动时域估计稳定的充分条件，提出利用估计的协方差矩阵计算到达代价，这也是目前计算到达代价的主流思路。基于文献[7]的研究成果，文献[13]采用卡尔曼滤波的误差协方差矩阵计算到达代价，文献[14-15]利用EKF计算到达代价，文献[16]则利用无迹卡尔曼滤波(UKF)计算到达代价。

这些方法都是从概率与统计的角度出发，且并未利用滚动时域估计的结果，因此是一类开环的到达代价计算方法，不利于进一步提高估计精度。针对这一问题，本文从动态规划原理出发，将到达代价的计算转化为最小二乘问题，并利用QR分解给出计算方法。该方法在到达代价的计算过程中使用了最新估计值，因而形成了反馈机制，有利于提高估计精度与速度。

1 弹性高速飞行器数学模型

本文主要研究弹性高速飞行器的纵向状态/参数估计问题，因此使用如下纵向动力学模型[17]：

(1)

本文考虑2种传感器布置方案。方案1采用常规的传感器输出：角速度信号ωm和过载信号nm。

(2)

式中:φi(x)为第i阶弹性模态的振型；xs为传感器的轴向坐标；nz为刚体模态产生的过载。

一般地，弹性高速飞行器仅一阶弹性模态与刚体运动及控制系统频带耦合[17-18]，因此本文仅考虑一阶模态。忽略长周期模态，且考虑弹性模态固有频率的变化，令

(3)

式中:δ为飞行器的舵偏角。

方案2采用分别安装在弹体前半部(距头部xs1)和后半部(距头部xs2)的2套陀螺[4]：

(4)

分别将上述信号作差，可得到与刚体运动无关的角速度信号分量ωe和受到弹性振动信号扰动的角速度信号分量ωr：

(5)

同样可令

(6)

综上，弹性高速飞行器的数学模型如下：

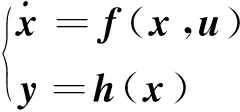
(7)

2 基于QR分解的滚动时域估计

2.1 问题描述

对于式(7)所示的连续系统，可利用差分、多重打靶等方法转化为式(8)所示的离散系统：

(8)

式中：wk和vk分别为系统噪声序列和量测噪声序列，通常情况下假设二者服从零均值高斯分布：

(9)

其中:Q和R分别为系统噪声和量测噪声的协方差矩阵。

系统式(8)的状态估计问题可转化为如下优化问题：

(10)

式中：

(11)

优化问题式(10)利用了全部的测量数据，因此称全信息估计。全信息估计的计算量会随T的增长而迅速增大到无法接受的地步，因此引入滚动时域策略以限制全信息估计的维数，形成滚动时域估计方法。滚动时域估计方法的目标函数ΦT变为

ΦT(xT-N,{wk})=CT-N(xT-N)+

(12)

式中：CT-N(xT-N)为到达代价，根据前向动态规划原理，其定义如下：

s.t.x(T,x0,{wk})=z

(13)

其中:x(τ,x0,{wk})表示在初值为x0且受到噪声序列{wk}的情况下τ时刻状态量的取值。

由式(13)可知，到达代价是一个表达式非常复杂的函数[19]。因此，一般用如下二次函数近似表示到达代价：

(14)

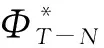
2.2 基于QR分解的到达代价计算方法

在T+1时刻，有

ΦT+1(xT-N+1,{wk})=CT-N+1(xT-N+1)+

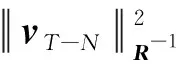
(15)

因此，利用式(14)所示函数估计到达代价，根据前向动态规划原理可得

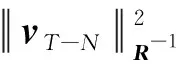
(16)

对权重矩阵PT-N、R-1和Q-1作Cholesky分解，有

(17)

利用式(17)，式(16)可写为

CT-N+1(xT-N+1)=

(18)

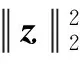
(19)

式中：

(20)

同理可得

(21)

式中：

(22)

将式(19)和式(21)代入式(18)可得

(23)

令

(24)

式(23)所示的到达代价计算问题转换为如下所示的最小二乘问题：

(25)

为求解式(25)所示的最小二乘问题，对A作QR分解。

(26)

式中:L为正交矩阵；R1和R2为上三角矩阵；R12为矩阵。

此外为表示方便，设

(27)

将式(26)和式(27)代入式(25)可得

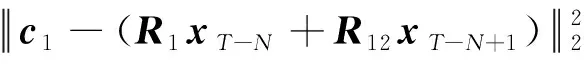
(28)

式(28)中的变量仅有xT-N，因此该最小二乘问题的解为

(29)

将式(29)代入式(28)可得

(30)

与式(14)比较即可得到到达代价的更新方程:

(31)

综上，到达代价的更新计算方法如下：

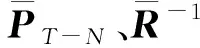
步骤2线性化函数F和H。

步骤3构造矩阵A和b。

步骤4对A进行QR分解。

并计算

即完成对到达代价的更新。

2.3 滚动时域估计问题的求解

由2.1节和2.2节可知，弹性高速飞行器的状态估计问题转化为固定维数的优化问题。但这需要对系统状态和输入进行采样，因此对于弹性高速飞行器这一连续系统，需要选用合适方法完成系统方程的离散。

考虑到系统非线性较强且采样速率恒定，因此选用离散节点间距恒定且精度较高的多重打靶法。多重打靶法在等间距的离散节点上对状态量和控制量进行离散，认为相邻节点间控制量恒定，并加入节点处状态量相等的约束，从而实现连续系统的离散化，最终将状态估计问题转化为式(32)所示的非线性规划问题。

(32)

本文采用较为成熟的序列二次规划方法求解非线性规划问题式(32)。

综上，滚动时域估计方法的步骤如下：

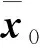
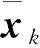
步骤3当k≥N时，利用序列二次规划方法求解非线性规划问题式(32)。

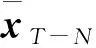
3 仿真分析

设窗口长度N=15，采样周期Δt=15 s，量测噪声协方差矩阵为R=diag([2.5×10-52.5×10-5])，系统噪声协方差矩阵为Q=diag([1×10-61×10-21×10-62.5×10-30.36])。系统输入信号如图1所示，为了验证不同输入下方法的性能，在前25 s为正弦信号，后25 s无输入。此外，为了验证滚动时域估计方法对参数的估计性能，对一阶弹性模态固有频率加入了正弦扰动信号。

在量测数据和估计初值相同的情况下，分别采用EKF、EKF更新到达代价的滚动时域估计(MHE-EKF)和QR分解更新到达代价的滚动时域估计(MHE-QR)对弹性高速飞行器的状态和一阶弹性模态的固有频率进行估计。

在传感器按照方案1布置的情况下，分别对上述3种方法进行100次Monte Carlo仿真。估计结果的均方根误差(Root Mean Square Error, RMSE)如图2所示。

图1 输入信号Fig.1 Input signal

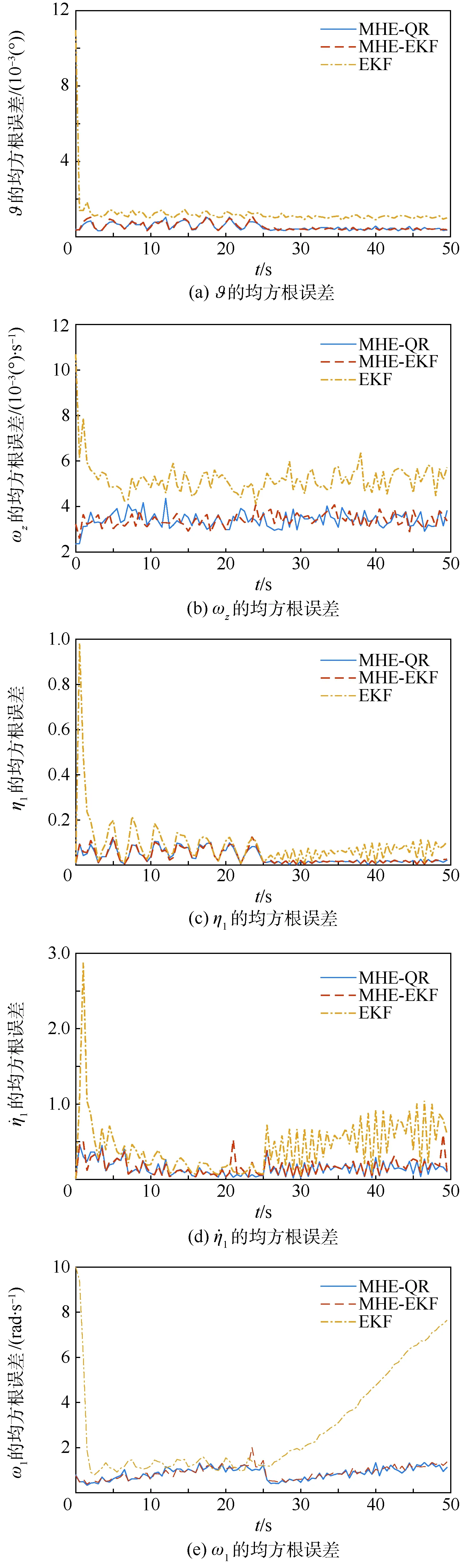
图2 EKF、MHE-EKF和MHE-QR方法估计结果的均方根误差Fig.2 RMSE of estimation results of EKF, MHE-EKF and MHE-QR methods

利用MHE-QR方法分别在传感器布置方案1(MHE-QR1)和传感器布置方案2(MHE-QR2)下进行100次Monte Carlo仿真，估计结果的均方根误差如图3所示。

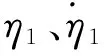
表1为上述方法的均方根误差均值。为验证估计弹性模态频率的必要性，表1还显示了只估计状态量的滚动时域估计方法(MHE-S)和EKF(EKF-S)的均方根误差均值。

由表1可知，MHE-QR和MHE-EKF的精度明显高于EKF。且MHE-QR对ω1的估计精度最高，MHE-EKF的估计误差大于MHE-QR，而EKF对ω1的估计出现了较大的误差。这是由于在滚动时域估计中，ω1只是一个优化变量，而噪声项只是提供了改变ω1取值的手段，对ω1的估计并不依赖具体的模型；而EKF将ω1看作状态量，对其的估计精度依赖于模型的准确度，但这类参数的变化并不存在具体的模型，因此EKF很难准确估计时变的参数。此外，只估计状态量的MHE-S和EKF-S的误差均明显大于其他3种同时估计参数和状态量的方法，说明对变化的参数进行估计是十分必要的。

表2显示了3种方法的计算耗时，仿真在Windows 10系统(CPU为i5-7400，主频为3.00 GHz)中MATLAB R2017a环境下完成。EKF的耗时明显短于MHE-QR和MHE-EKF。MHE-QR的平均计算耗时短于MHE-EKF，且MHE-QR的最大计算耗时低于采样周期，具备应用潜力；而MHE-EKF虽然平均计算耗时低于采样周期，但最大计算耗时高于采样周期，表明EKF更新到达代价在计算效率上不如QR分解。

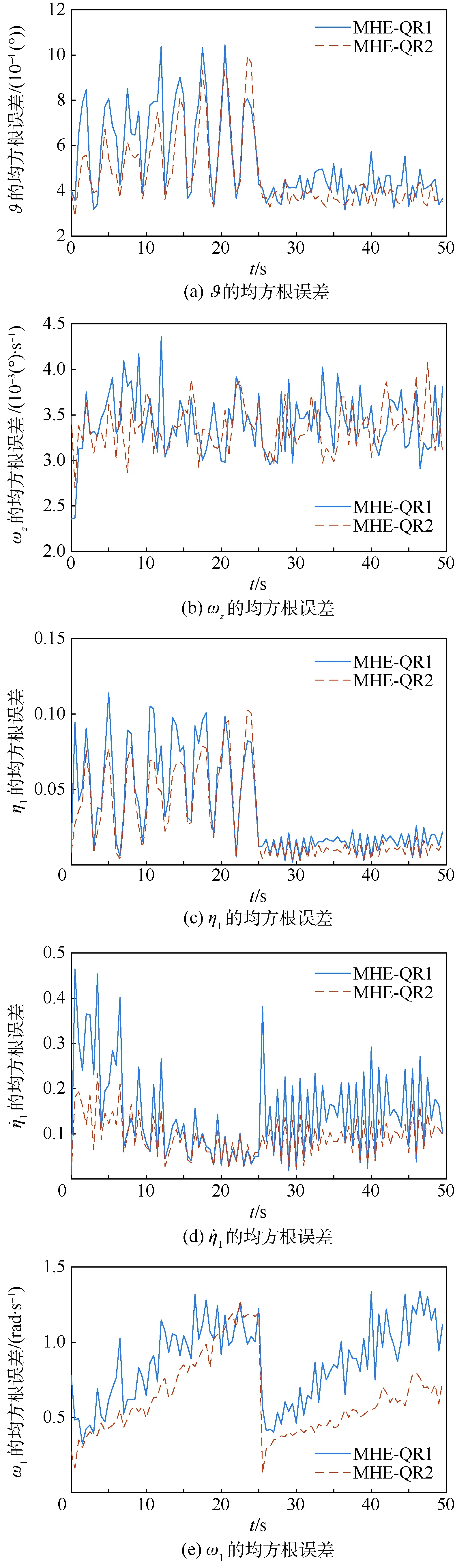
图3 不同方案时MHE-QR方法估计结果的均方根误差Fig.3 RMSE of estimation results of different schemes using MHE-QR method

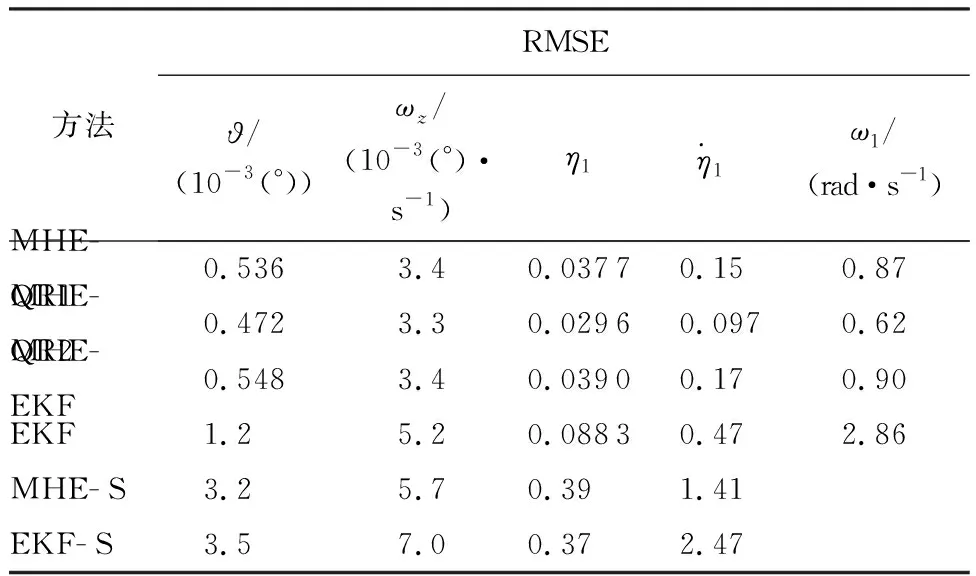
表1 不同方法估计结果的均方根误差均值Table 1 Average RMSE mean values of estimation results of different methods

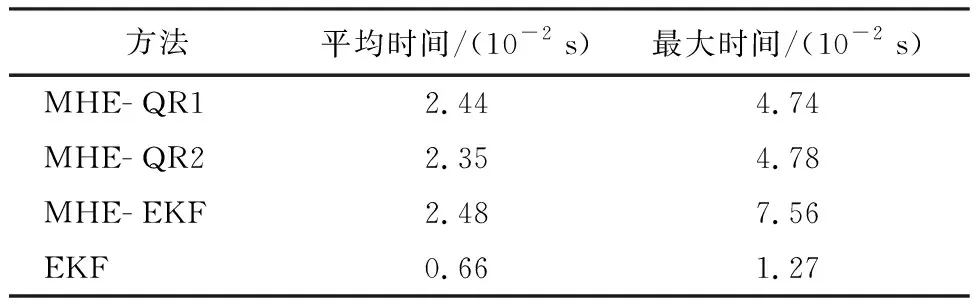
表2 不同方法的计算耗时Table 2 Run time of different methods

4 结 论

本文提出了一种基于QR分解的到达代价更新方法，并将其用于弹性高速飞行器的滚动时域估计中，实现了状态/参数联合估计。

1) 状态/参数联合估计方法的精度远高于只估计状态的方法。由于弹性高速飞行器弹性模态的固有频率并非常数，会随飞行器状态变化而变化，因此对其进行在线估计是非常必要的，能够有效提高状态估计的精度。

2) 滚动时域估计的精度明显高于EKF。相较于传统的EKF更新方法，QR分解更新到达代价在精度类似的同时，具有更快的计算速度(最大计算耗时优于EKF)。这得益于QR分解更新到达代价的策略利用了滚动时域估计的结果，形成了反馈机制，并通过直接求解优化问题更新到达代价。

3) 传感器采用布置方案2时的滚动时域估计结果好于布置方案1。这是由于方案2通过引入有效信息预估而进一步提升了估计效果。

4) QR分解更新到达代价的滚动时域估计方法的最长计算耗时低于采样速率，具有实际应用的潜力，后续应继续研究更快的优化算法，提高计算速度。