一种考虑过滤的短纤维增强复合材料RVE建模方法
刘丰睿, 骈瑢, 赵丽滨, 张建宇
(1. 北京航空航天大学 宇航学院, 北京 100083; 2. 重庆大学 航空航天学院, 重庆 400044)
短纤维增强复合材料具有比强度高、比刚度高和可设计性强等特点,在航空航天[1-2]、建筑[3]、汽车[4]、医疗[5]、船舶[6]等领域应用广泛。其弹性模量的预测是重要的研究内容,主要的预测方法有均匀化法[7]、代表性体积单元(Representative Volume Element,RVE)法[8-10]等。其中,RVE法考虑因素多,能全面预测材料特性,是常用的预测方法。高效地建立RVE是进行材料性能预测的第一步,也是研究难点。
目前建立短纤维增强复合材料RVE的方法有:随机顺序吸附(Random Sequential Adsorption, RSA)方法[10-12]、基于RSA的纤维生长法[13]、分子动力学方法[14]、粒子群优化算法[15]、蒙特卡罗方法[16]和图像重建技术[17]等。其中,RSA方法凭借其操作简单、计算量小的优点被广泛应用。该方法的核心是每次在RVE区域内生成位置随机、取向按给定函数随机分布的一根纤维后,判断新纤维与已存在纤维是否相交,仅当不相交时认为新纤维可以存在于RVE中,循环此过程直到纤维体积分数达到规定值为止[10]。纤维相交与否关系的判断通常通过几何方法实现[18]。考虑到几何方法计算复杂且计算量大,Liu等[19]采用布尔运算方法判断纤维是否相交,进而提出了基于布尔运算的随机顺序吸附(Boolean Operation based Random Sequential Adsorption,BORSA)方法。但是,布尔运算判断法耗时也较长,并且对一些非常容易判断位置关系的纤维进行布尔运算判断影响了RVE的建立效率。
本文对Liu等[19]的方法进行了改进,在对纤维进行布尔运算判断前,加入了新纤维与已存在纤维的形心距计算,当形心距小于规定距离时不进行布尔运算,直接重新随机生成纤维位置,这相当于过滤掉了部分随机生成的新纤维,进而提出了考虑过滤的随机顺序吸附(Filter based Random Sequential Adsorption,FRSA)方法。然后,采用RVE生成算例验证了方法的先进性。
1 BORSA方法

1) 生成第1根纤维fi(i=1)。随机生成符合均布函数的纤维形心位置参数(x1,y1,z1),随机生成符合相应函数的取向参数(θ,φ),并在模型中生成纤维。

3) 随机生成纤维fi的参数(xi,yi,zi,θi,φi)。设定布尔运算次数T=0。
4)T=T+1,将纤维fi向(±L,0,0),(0,±W,0),(0,0,±H),(±L,±W,0),(0,±W,±H),(±L,0,±H),(±L,±W,±H)共26个方向复制。然后执行布尔运算:用27个新纤维fi减现有的i-1根纤维,当i-1根纤维的剩余体积小于(i-1)Vf时,表明纤维间有相交关系,进行步骤5);当i-1根纤维的剩余体积等于(i-1)Vf时,认为纤维fi与纤维fj(j=1,2,…,i-1)均不相交,进行步骤6)。
5) 当T 6) 保存纤维fi的信息,返回步骤2)。 由上述过程可见,每生成一根纤维或对纤维进行一次平移,均需进行一次布尔运算。由于纤维位置是随机生成的,其中必然存在新生成的纤维形心位置与现有纤维形心非常接近的情况,比如小于纤维直径,此时的新纤维必然与现有纤维相交。如果通过设置过滤函数使得对这部分新纤维不需要进行布尔运算,则可以提高RVE生成速度。 为了实现纤维过滤,定义新生成纤维与现有纤维形心距最小值di为 di=min(dij) (1) 式中:dij为纤维fi和fj的形心距离,定义为 (2) 并在进行布尔运算前判断di是否小于一个常数dc(dc为临界距离)。当di 空间中2个纤维的距离dij存在2个特殊情况: 1) 当dij=D时,以fi形心为球心的纤维内切球体与以fj形心为球心的纤维内切球体相外切,如图1所示。 根据上述2种情况可以将纤维之间的相交关系分为必然相交、必然不相交和可能相交3种情况: 1) 当0≤dij 则dc的取值会导致4种过滤状态: 1) 当0 图1 fi内切球体与fj内切球体相外切Fig.1 Circumscribed inner spheres of fi and fj 图2 fi外切球体与fj外切球体相外切Fig.2 Circumscribed outer spheres of fi and fj 2) 当dc=D时,过滤掉的fi是一定与fj相交的,并且一定与fj相交的fi均被过滤掉。 由上述分析可知,如果dc FRSA方法将生成RVE的步骤4)改为:计算fi与fj(j=1,2,…,i-1)形心距的最小值di。当di 需要指出的是,为了避免降低计算效率,上述方法中计算di时没有对跨边界纤维进行特别处理。 考虑到过滤法是通过减少布尔运算次数提高建模效率的,图3给出采用BORSA方法和FRSA方法,各生成1个RVE模型时,生成每根纤维的布尔运算次数。 采用2种方法各生成10个RVE。计算生成一个RVE的总布尔运算次数,并对10个RVE取平均值,可知BORSA方法和FRSA方法生成一个RVE的平均布尔运算次数分别为87.5和61.8次,改进后FRSA方法布尔运算次数降为BORSA方法的70.6%。 建模效率的最好指标是建模时间。比较2种方法各生成10个算例的总时间,发现BORSA方法耗时1 079 s,改进后FRSA方法耗时921 s,可见建模时间降为原方法的85.4%,明显提高了RVE的建模效率。 采用FRSA方法生成的一个RVE如图4所示,可以用来进行后续的材料性能分析。 图3 改进前后2种方法在一个RVE算例中每根纤维的布尔运算次数Fig.3 Number of Boolean operation times per fiber in one RVE example with two methods before and after improvement 图4 FRSA方法生成的RVEFig.4 RVE generated with FRSA method 表1 不同情况下的RVE建模效率对比Table 1 Comparison of RVE modeling efficiency for 3.2.2dc对建模效率的影响 分别计算2种方法生成一个RVE所需时间的比值t′/t″,并对10次模拟数据取平均值,结果如表2所示。 3.2.3AR对建模效率的影响 取AR=4、6和8 3种情况分别进行RVE生成模拟,以验证FRSA方法在不同AR取值下的改进效果。RVE建模所需时间的比值的10次模拟平均值如表3所示。 结合表1、表2和表3,AR=4、6和8 3种情况下结果可见,FRSA方法生成RVE的用时比BORSA方法均有所减少,验证了FRSA方法在不同AR取值下均具有先进性。并且,相同的dc取值条件下,AR取值越小,建模时间减少越明显,建模效率提高的程度越大。AR取值越大,建模效率改进效果降低,是因为在相同dc取值条件下,当AR取值增大时,临界距离dc与纤维外切球直径的比值减小,导致过滤程度降低,从而导致了方法改进效果的下降。 表2 不同dc情况下的RVE建模时间比Table 2 Ratios of RVE modeling time for various dc 表3 不同AR情况下的RVE建模时间比Table 3 Ratios of RVE modeling time for various AR 本文通过在BORSA方法进行布尔运算前引入纤维形心距判断,过滤掉大量可能与已存在纤维相交的新纤维,提出了FRSA方法。在不同RVE参数和方法参数下对比了2种方法的纤维布尔运算次数和建模时间,证明了FRSA方法的先进性。主要结论如下: 1) 依据形心距可将纤维位置关系分为必然相交、必然不相交和可能相交3种情况。 2) 可通过纤维形心距判断,过滤掉所有必然相交和部分可能相交的纤维。 3) FRSA方法能够提高RVE的建模效率,且效率提高程度随纤维体积分数增大而增加,随纤维长径比增大而减少。 4) 增大临界形心距可以增加改进效果,但是更易出现纤维拥塞现象。2 FRSA方法
2.1 FRSA方法原理
2.2 临界距离dc对FRSA方法的影响



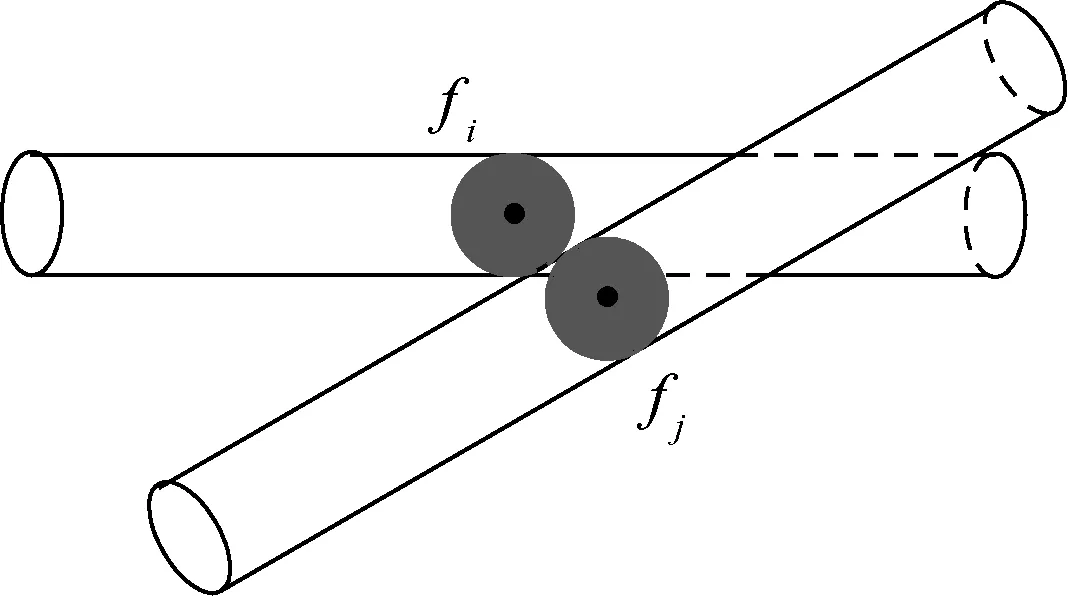

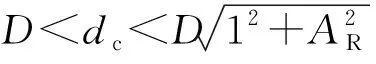
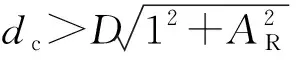
2.3 FRSA方法步骤
3 FRSA方法先进性验证
3.1 典型参数下的FRSA方法先进性验证

3.2 RVE参数和方法参数对FRSA方法先进性的影响

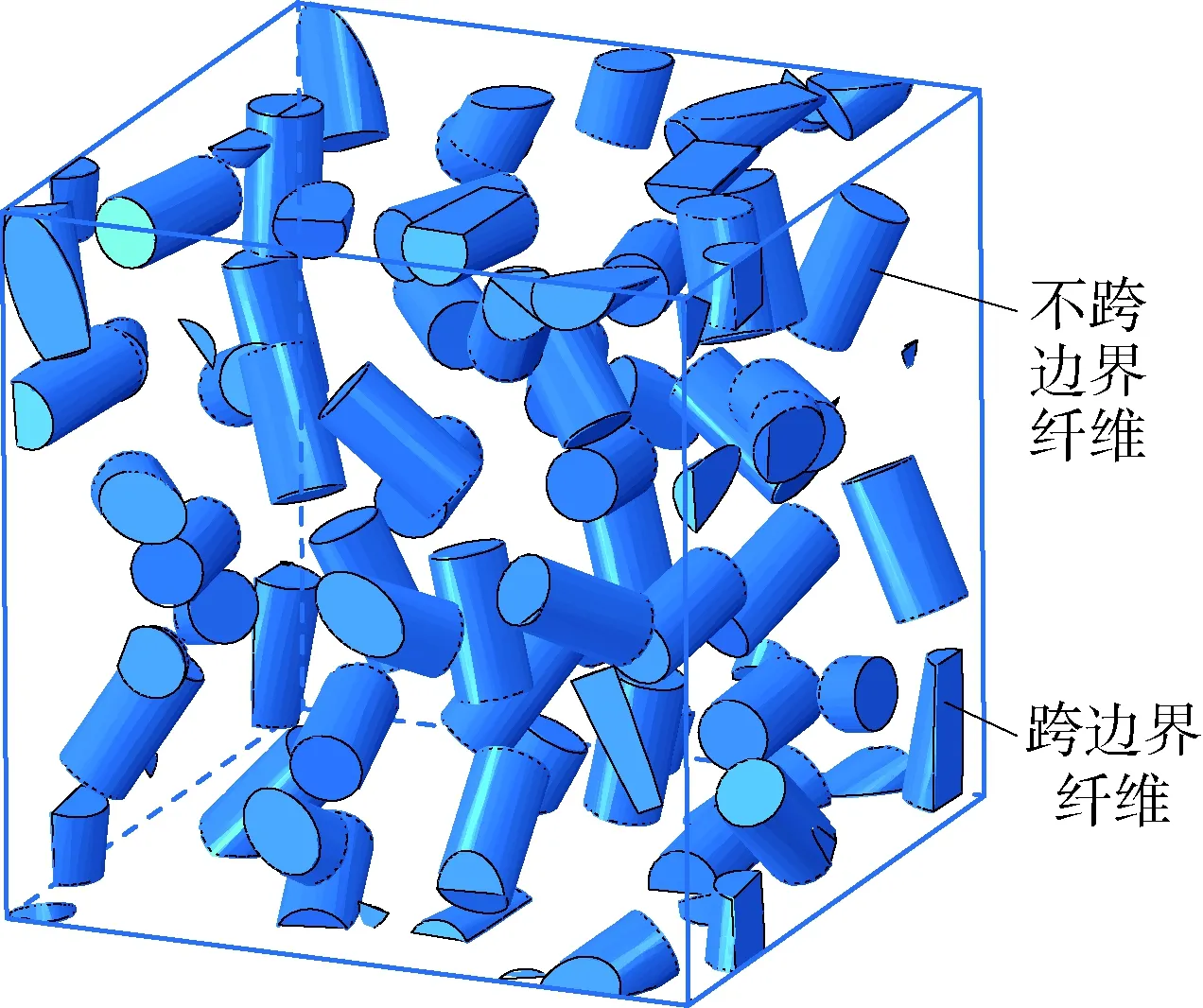



4 结 论

