基于混沌粒子群优化的北斗/GPS组合导航选星算法

王尔申， 贾超颖， 曲萍萍， 黄煜峰， 庞涛， 别玉霞， 姜毅

(1. 沈阳航空航天大学 电子信息工程学院， 沈阳 110136； 2. 北京航空航天大学 电子信息工程学院， 北京 100083; 3. 沈阳航空航天大学 辽宁省通用航空重点实验室， 沈阳 110136；4. 大连海事大学 水上智能交通行业重点实验室， 大连 116026)

随着全球卫星导航系统(Global Navigation Satellite System, GNSS)的不断建设和完善，由多个系统支持的组合导航成为了可能。组合导航使得可见卫星数大大增加，获得远比单一星座更优的卫星几何结构和更多的导航冗余信号，同时也加大了接收机的信号处理负担[1-2]。此外，导航信号在传播过程中还会受到电离层延迟、对流层延迟、建筑物遮挡、电磁波干扰等因素的影响，接收机很难接收到全部可见卫星。为此，根据导航需求，在定位之前粗略判别接收机所在位置的可见卫星分布，从中选择一个卫星子集进行定位解算。通过最小化几何精度因子(Geometric Dilution of Precision, GDOP)来获得最佳卫星子集的算法称为最优选星算法；以使接收机与可见卫星构成空间体积尽可能大，选择卫星子集最佳的算法称为最大体积算法。对于单一系统，由于定位和时钟偏差，定位所需的卫星最小数目为4颗[3]，而对于组合导航，由于不同系统的时钟偏差有所差异，用于定位的卫星数目最少为5颗[4]。因而，对于组合导航选星算法通常选择超过5颗卫星来尽可能提高定位精度。

现有的快速选星算法主要集中在2个方面：①从所有可见卫星中选择最佳卫星几何分布的某些可见卫星。研究者根据最优选星方案的卫星分布特点，利用卫星高度角和方位角信息实现卫星的区域划分，并对如何分配高仰角和低仰角的选星数目展开讨论[5-6]。②GDOP的计算。GDOP通常可看作是接收机测量误差与定位误差之间的放大倍数，是用来衡量从m颗可见卫星(m>n)中选择出的n颗卫星子集是否具有较好的空间几何分布的重要指标。GDOP的计算存在矩阵相乘和求逆过程，明显增加了选星的计算量。若实现快速选星，可通过求逆引理等方法简化求解GDOP的计算公式[7]，也可以采用优化算法尽可能减少GDOP的计算次数[8-10]，二者都能在一定程度上缩减选星耗时。2010年，Mosavi和Divband[8]提出用遗传算法(GA)实现选星，通过GA的快速寻优能力减少GDOP的计算次数。然而GA选星存在易陷入局部最优的问题，研究者又对算法进行大量改进，提高了算法选星结果的准确性[9-10]。但由于GA的计算过程需要调节的参数过多，所以在保证选星准确性的条件下，GA选星速度也会随着可见卫星数目的增加而减慢。

与GA类似，粒子群优化(Particle Swarm Optimization, PSO)算法是一种随机寻优算法。目前该算法已经在目标跟踪、图像处理等诸多领域得到应用[11-12]，但在多星座选星方面少有文献提及。本文针对PSO算法在组合导航选星上的应用进行研究，建立了PSO选星算法模型；引入混沌序列改进算法，提高选星有效性；通过实际的导航数据进行仿真实验，验证所提算法的性能。

1 混沌粒子群优化模型

在多星座组合卫星导航系统中，为了降低接收机的运算量，需要从可见的所有卫星中选出空间结构较优的一组用于定位。精度因子(DOP)常用来衡量卫星空间几何分布情况，其计算公式中存在矩阵相乘和求逆，是选星中比较耗时的运算。而PSO算法能够通过有限次迭代，从全部解空间中快速搜索到符合条件的目标解。因此，运用PSO算法的快速寻优能力，从全部可见卫星组合中快速选取空间几何分布较好的卫星组合，能够减少DOP的计算次数，从而减少选星的耗时。

PSO算法是Eberhart和Kennedy通过模仿鸟类的觅食行为而产生的[13]，搜索空间的个体通过比较自身所经过的最优位置和种群中其他粒子最优位置，不断调整自身速度，使其向最优解靠拢。个体被称为“粒子”，每个粒子为d维空间的一个点，第i个粒子可以表示为xi=[xi1,xi2,…,xid]，粒子在运动过程中，会根据自身经验产生个体极值pbest=[pi1,pi2,…,pid]，同时在种群中会产生全局极值gbest，粒子通过2个“极值”不断调整自身位置，位置更新如式(1)所示，使其不断趋近全局最优值。第i个粒子的位置变化速度被表示为vi=[vi1,vi2,…,vid]。

vid(t+1)=ωvid(t)+c1r1(pbest-xid(t))+

c2r2(gbest-xid(t))

(1)

xid(t+1)=xid(t)+vid(t+1)i=1,2,…,N

(2)

式中：t为当前迭代次数；N为种群中粒子的总数；ω为惯性权重；c1和c2为加速常数，分别调节向pbest和gbest方向的运动速度；r1和r2为0～1之间均匀分布的随机数。另外，通过设置微粒的速度范围[vmin,vmax]和位置范围[xmin,xmax]，可以对粒子运动的步长进行适当的限定。

惯性权重ω对全局和局部搜索的平衡起到了重要作用，其值通常是从0.9～0.4线性递减的[14]。在迭代过程中，表达式为ω=ωmax-(ωmax-ωmin)t/tmax，ωmax和ωmin分别为最大和最小惯性权重，tmax为总的迭代次数。

PSO算法的结果容易陷入局部最优，为此引入混沌理论，提高结果的有效性。混沌搜索，即对于给定的优化函数，将变量从混沌空间映射到解空间，然后利用混沌变量进行搜索[15]，可避免搜索结果陷入“局部最优”。

Logistic映射是较为常见的混沌序列产生方法，其表达式为

zi+1=f(zi)=μzi(1-zi)i=0,1,…

(3)

式中：zi∈(0,1)。当z0∉{0,0.25,0.5,0.75,1}、μ=4时，Logistic映射产生混沌序列。利用Logistic映射初始化均匀分布的初始粒子，能够增强PSO算法的稳定性[16]。

首先生成(0,1)的随机数zi，根据式(3)更新zi，然后根据公式xi=ximin+zi(ximax-ximin)，将混沌空间映射到待优化的解空间。

2 北斗/GPS组合导航选星算法

2.1 混沌粒子群优化适应度函数

适应度函数又称为目标函数，是用来评价粒子优劣的重要衡量标准，适应度函数的选取直接影响算法结果的有效性。本文采用的适应度函数是各可见卫星组合的GDOP值，用于评价所选卫星组合的空间几何结构性能。

选星算法主要以用户与可见卫星组合的空间几何分布为衡量标准。针对用户与可见卫星组合的空间几何分布特性的表征，DOP是应用最广泛的参数，按照DOP进行选星可以保证定位精度[1]。卫星导航定位系统的DOP可用GDOP与用户等效测距误差(User Equivalent Range Error，UERE)的乘积来表示，即

σp=GDOP·σUERE

(4)

式中：σp为导航定位位置/时间解的精度；σUERE为伪距测量值的标准差；GDOP与用户到卫星的几何结构有关。从式(4)可知，当σUERE确定时，GDOP越小，定位精度越高。

GDOP可定义为协方差矩阵的迹的平方根，即

(5)

式中：trace(·)表示矩阵的迹；H为观测矩阵。假设北斗/GPS组合导航接收机能接收到m颗GPS卫星、k颗北斗卫星，即可产生m+k个观测量，构成的观测矩阵为

(6)

式中：(ei,ni,ui)为接收机近似位置指向第i颗卫星单位矢量的方向余弦，下标G代表GPS星座，可见星数目为1，2,…，m,下标B代表北斗星座，可见星数目为1，2,…，k。

2.2 混沌粒子群优化选星算法设计

假设某时刻接收机接收到可见卫星总数为n颗，从中选取m颗，使其GDOP值尽可能小。在混沌粒子群优化(CPSO)算法选星中，每个粒子代表一种可见卫星组合，粒子的位置由m个元素决定，每个元素代表一颗可见卫星，CPSO选星算法具体步骤如下：

第二，重新评估开放获取中采取的部分措施和手段。过去科学工作者出版时一般不需要考虑钱的问题，而向开放获取期刊投稿时需要自筹出版处理费，这样不仅加重了科学工作者的负担，而且将以付费为基础的学术传播作为一种模式固化下来。出版商在开放获取中形成的混合开放获取模式，虽然增加了开放获取资源的范围和数量，但并没有起到实质性的作用。

步骤1可见卫星提取。根据导航电文，提取当前时刻仰角大于遮蔽角的卫星(本文中的遮蔽角取值为5°)，得到该时刻的可见卫星总数。

步骤2编码。对当前时刻接收机观测到的所有可见卫星进行随机排列，然后将可见卫星从1,2,…,n依次连续编码，编码与可见卫星一一对应。

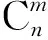
步骤4适应度的计算。本文采用的适应度函数是编码所对应的可见卫星组合的GDOP，记为粒子的目标值fti=GDOPi，下标“t”为粒子经过t次迭代。将初始种群中的粒子依次代入适应度函数中，得出各粒子的适应度值(即GDOP)。将种群中GDOP最小的粒子设置为初始种群最优位置gbest，每个粒子当前的位置gt,i为初始个体最优位置pbest。

步骤5更新。对于每个粒子，根据式(1)和式(2)不断修正种群中粒子的位置xti和速度vti，分别计算新位置对应的目标值fti，并更新粒子所经过的最优位置pbest和种群最优位置gbest。直到达到最大迭代次数，终止迭代。

将CPSO算法应用到选星过程中，需要明确3个量：初始化粒子种群、选取适应度函数和速度位置的更新，其基本步骤流程如图1所示。

在算法流程中，粒子更新时需注意2个关键点：①可见卫星编号为整数，因此更新过程中必须

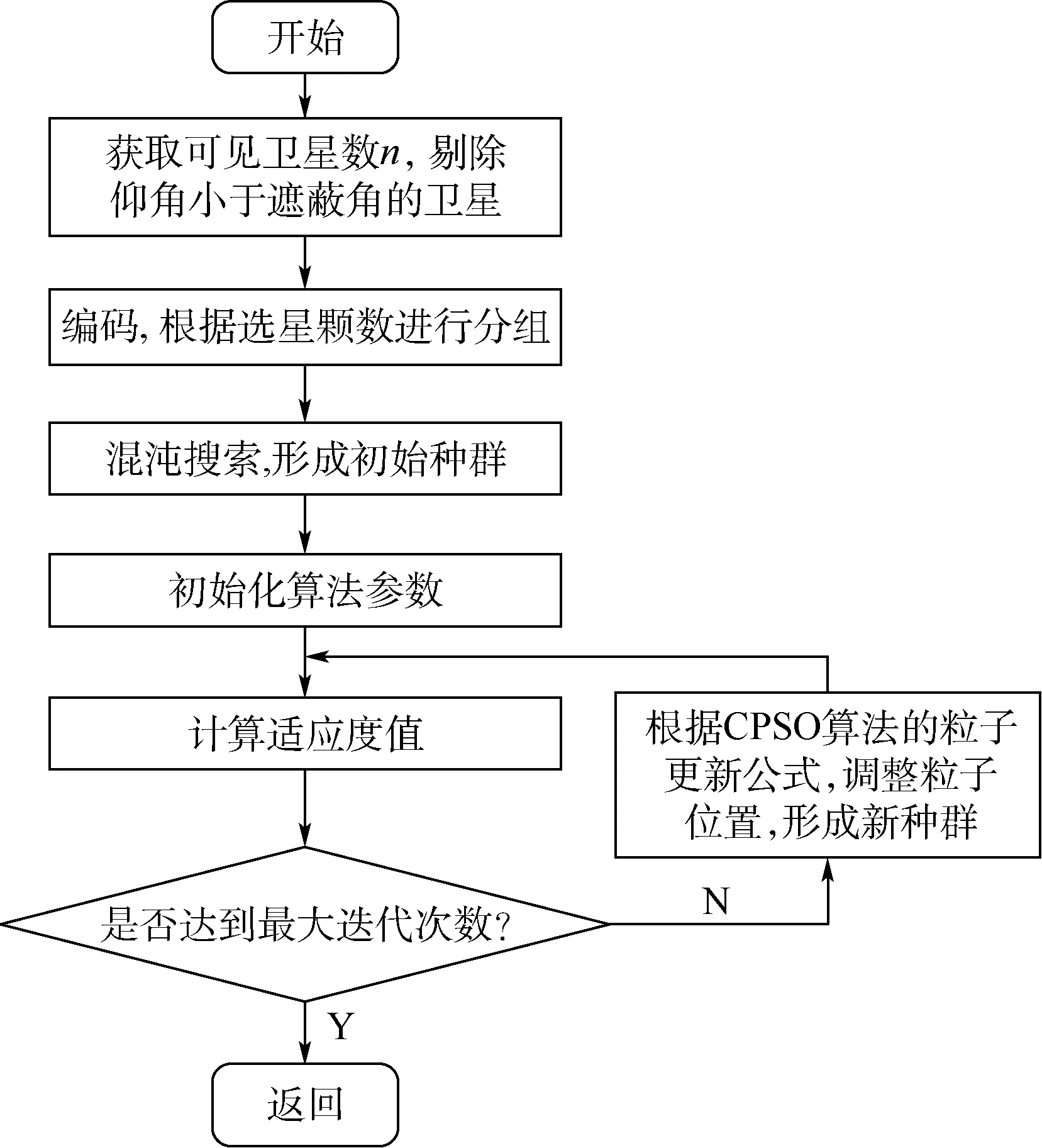
图1 CPSO选星算法流程Fig.1 Flowchart of CPSO satellite selection algorithm

保证粒子位置中的每个元素都为整数，否则将找不到与编码对应的可见星；②选星颗数为m颗，如果粒子位置中的元素有相同的，选星颗数就会少于m颗。为了保证选星数目，每次更新都必须判断更新后的粒子位置中是否有相同元素。本文给出的解决办法是在粒子进入迭代循环后，首先判断每个粒子中是否存在相同的元素。如果存在相同元素，则对粒子中元素从小到大排序，找出相同元素的个数及位置，在与之重复的第k个元素值上加k，然后返回重新判断是否有重复元素，直到该粒子中无相同元素为止。

3 仿真验证与结果分析

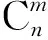
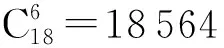
按照PSO选星步骤，设定算法参数：迭代次数MaxIt=50，种群大小M=100，惯性权重ω=0.729 8，加速常数c1=c2=1.496 2，vmax=2。选取某一时刻进行GDOP值的计算，随着迭代次数的增加GDOP值的变化如图3所示。

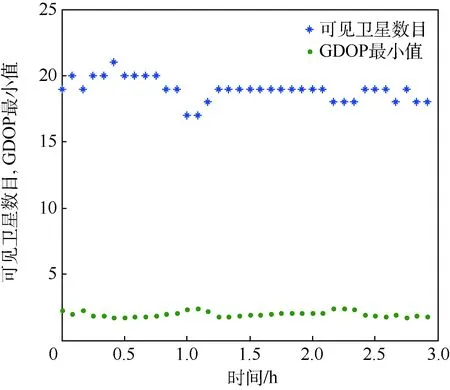
图2 北斗/GPS可见卫星数及对应的GDOP最小值Fig.2 Number of BDS/GPS visible satellite and their minimum GDOP

通过遍历法得出该时刻的GDOP最小值为2.25。图3中的结果显示，PSO算法的收敛速度很快，迭代次数在小于15次时就稳定在2.34附近，且在后续迭代过程中保持不变。很明显，PSO算法出现“早熟”现象，即陷入局部最优解。

采用CPSO算法对同一时刻进行仿真实验，结果如图4所示。

从图4中可以看出，CPSO算法同样在迭代次数低于15次时收敛，并有效改善了PSO选星算法易陷入局部最优的缺点。在迭代次数为50次时，耗时约为1.5 s左右，如果按需求适当减少迭代次数，选星耗时也会有所减少。

遍历法、PSO和CPSO选星算法在相同历元的选星耗时及其对应的选星结果(最后一列数字代表卫星号)如表1所示。

从表1中数据得知，基于PSO和CPSO的选星算法在单次选星所用时间约为遍历法选星的37.5%，但选星结果仍有偏差。为了充分验证算法性能，下面将给出仿真时长为3 h的PSO和CPSO选星GDOP计算误差，其误差定义为新算法所得到的GDOP值与遍历法选星所得到GDOP值的差值，结果如图5所示。

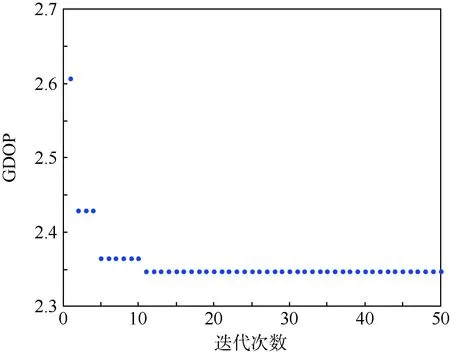
图3 PSO选星时GDOP值随迭代次数的变化Fig.3 Change of GDOP with iteration numbers of PSO satellite selection

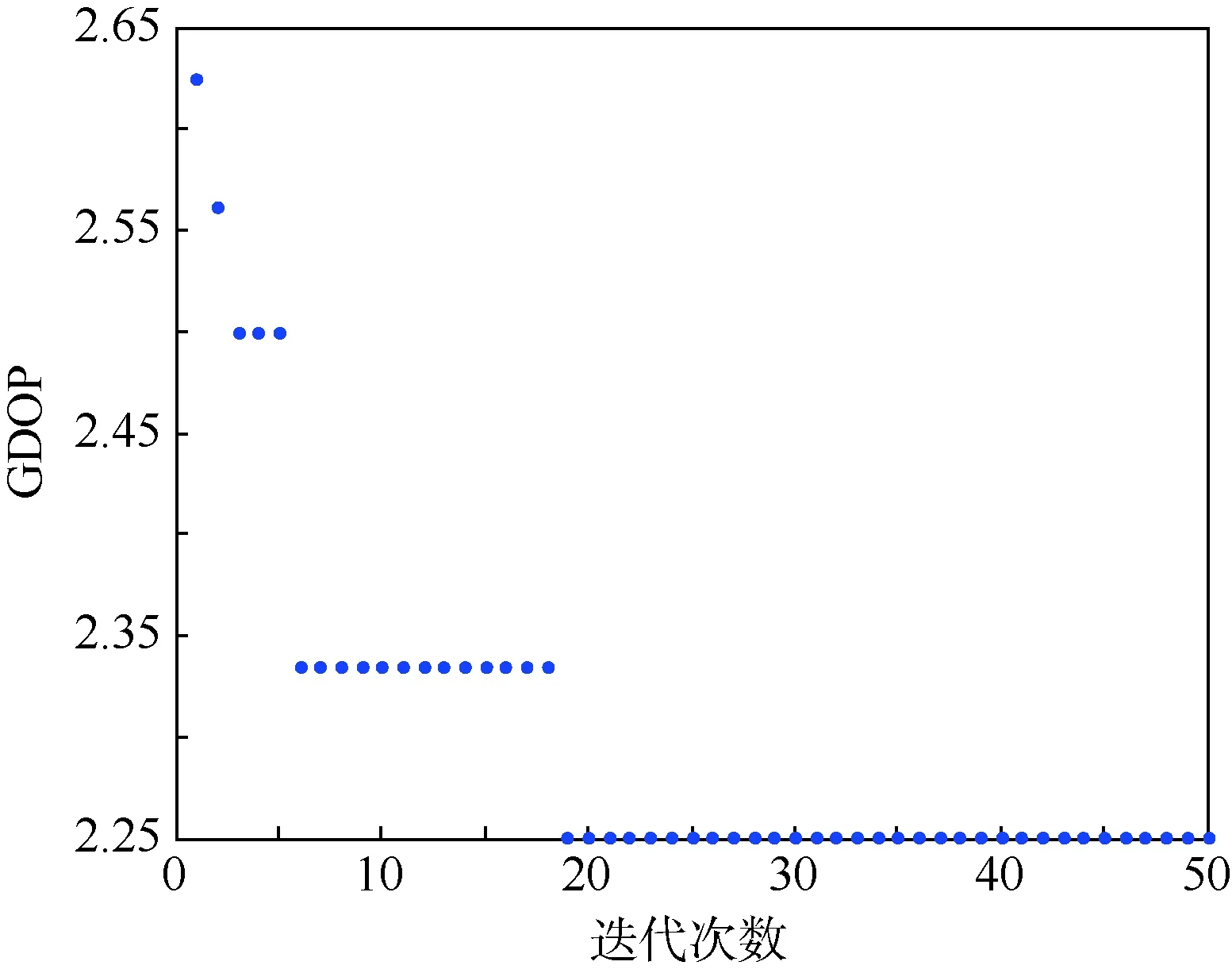
图4 CPSO选星时GDOP值随迭代次数的变化Fig.4 Change of GDOP with iteration numbers of CPSO satellite selection

从图5中可知，PSO和CPSO选星算法的GDOP计算误差均小于等于0.6。对所得数据进行统计，CPSO选星的GDOP计算误差平均值为0.260 9，方差为0.042 4；PSO选星的GDOP计算误差平均值为0.263 2，方差为0.043 0。

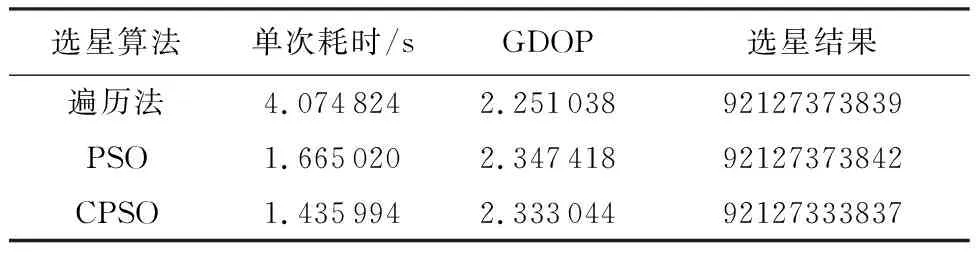
表1 三种选星算法性能对比Table 1 Performance comparison of three satellite selection algorithms

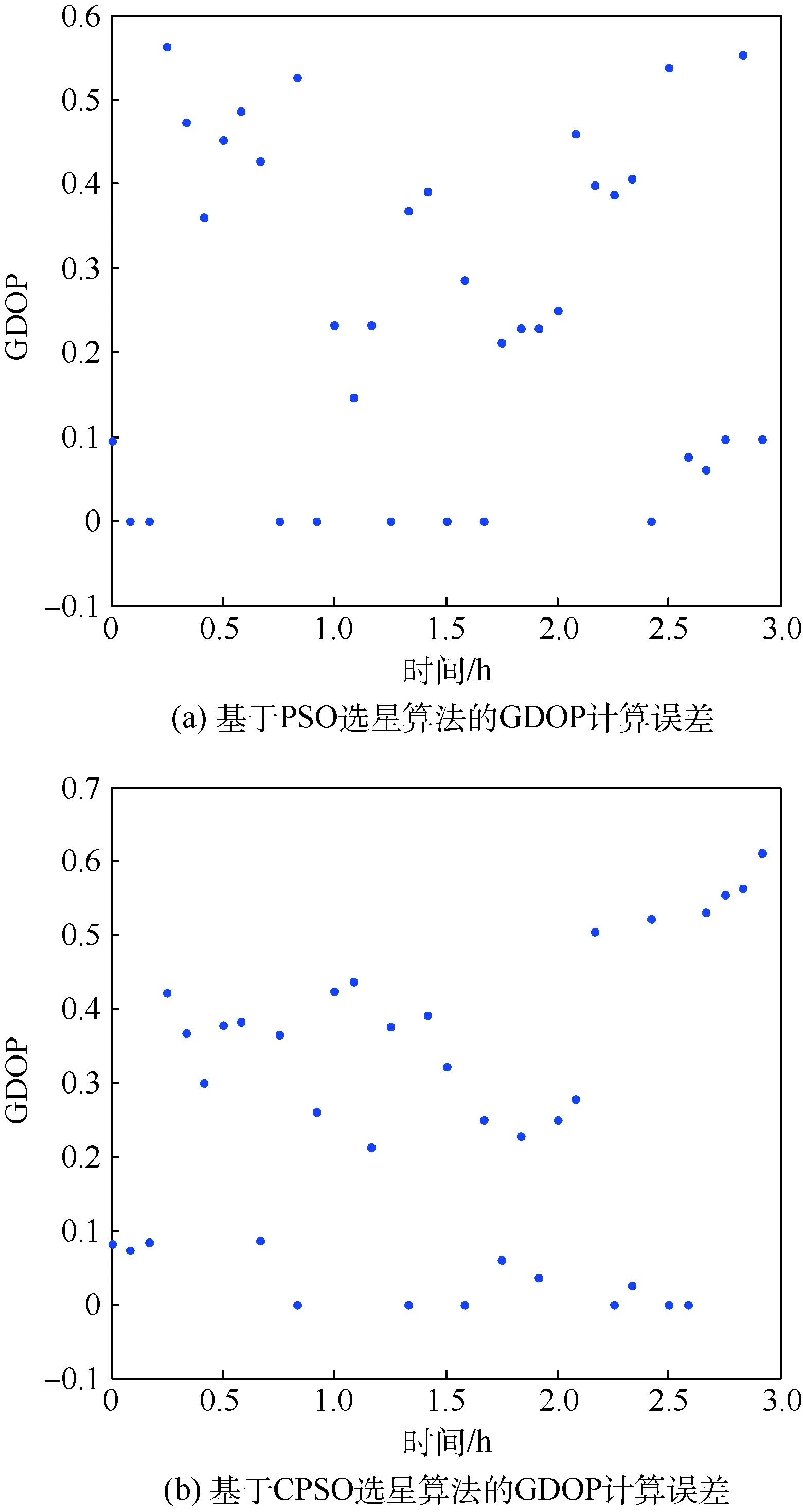
图5 PSO和CPSO选星的结果误差Fig.5 Result error of satellite selection by PSO and CPSO

4 结 论

本文提出了一种基于CPSO的北斗/GPS组合导航选星算法，利用CPSO算法的快速寻优能力，减少GDOP的计算次数，从而实现了北斗/GPS组合导航快速选星，通过对算法进行仿真验证，得到以下结果：

1) 在北斗/GPS组合导航下，选星颗数为6时，算法能够实现快速选星。该算法的单次选星时间约为1.5 s，约为遍历法选星的37.5%。

2) 利用混沌方程初始化种群粒子能够提高选星结果的准确性。

3) PSO和CPSO选星算法的GDOP计算误差均小于等于0.6，二者的平均计算误差约为0.26。

本文将CPSO算法应用于组合卫星导航选星过程中，为多星座组合导航快速选星问题提供了新的解决方法。