湿法脱硫浆液pH值优化控制的设计及应用

董庆武，郑国强

（福建龙净环保股份有限公司，福建 龙岩 364000）

1 背景

在石灰石-石膏湿法烟气脱硫工艺中，吸收塔浆液pH值的控制是影响脱硫效率和脱硫设备稳定运行的关键因素。pH值太大，有利于对烟气中SO2的吸收，但不利于CaCO3溶解及CaSO3·1/2H2O的氧化，且易造成结垢。反之pH值太小，有利于CaCO3溶解及CaSO3·1/2H2O的氧化成CaSO4·2H2O，但不利于对烟气中SO2的吸收[1]。

由于脱硫浆液pH值反应滞后时间长，非线性、扰动因素多等特点，同时难以用经典或现代控制理论建立精确的数学模型，因此，采用常规PID控制不能及时跟踪系统的变化，也无法保证系统稳态的控制精度。当燃煤电厂根据需要变更燃煤含硫量、锅炉负荷等系统参数时，易引起控制系统运行的不稳定，需人工干预进行调整控制参数。

2 常规pH值控制

吸收塔石灰石浆液的供给由石灰石浆液箱底部引出管道，经供浆泵输出后分为两路，其中一路经吸收塔的供浆调节阀实现供浆及供浆流量的调节，另一路则通过回流返回石灰石浆液箱，如图1所示。

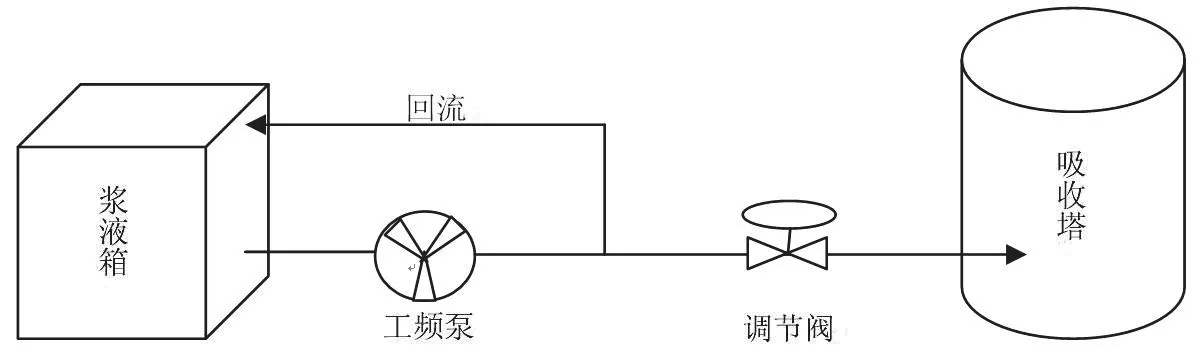
图1 吸收塔供浆管路

这种供浆方案的控制策略通常采用前馈-串级控制，如图2所示。串级反馈包括外环和内环两个PID控制。外环PID根据浆液pH测量值与设定值的偏差经PID控制器运算后的输出值叠加前馈输出得到石灰石浆液流量给定值。内环PID根据石灰石浆液流量给定值与流量测量值的偏差经PID控制器运算后输出控制调节阀的开度，完成石灰石浆液pH值控制。锅炉负荷前馈在一定程度上克服浆液pH值控制的滞后性，但在锅炉工况发生变化时，串级控制无法及时快速跟踪，易发生超调退出自动控制。

3 自优化模糊串级控制的pH值控制

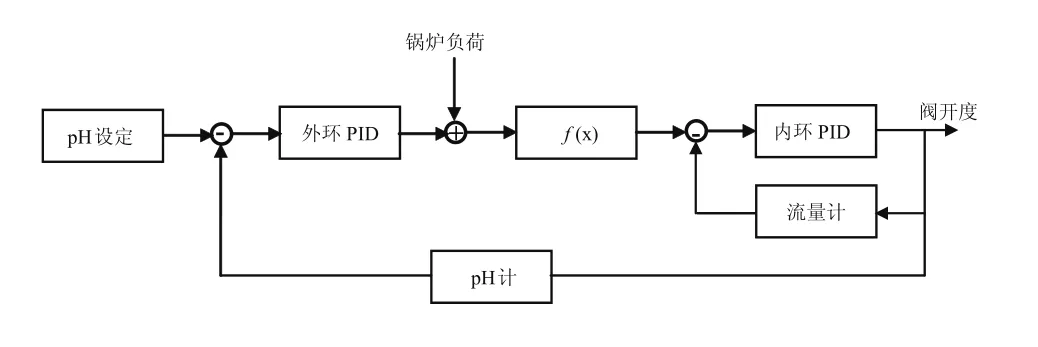
图2 常规前馈-串级控制原理图

针对浆液pH控制这种时变、非线性、大时滞的复杂系统，常规控制器往往无法实现较为理想的动态特性，但是若由具有丰富经验的操作人员控制时，则比较容易实现。这是因为现场操作人员通过实践操作，可以得到大量的以定性表述的经验数据，凭借操作经验，可采取适当的对策进行控制参数调整。针对这种现象，通常利用具有智能化的模糊控制器，将操作人员的控制经验描述成一组条件语句，再通过模糊集合理论将其定量化，使控制器能够接受人的操作经验，并模仿人的操作[3]。

为了减小调试过程中的工作量，以及在机组负荷发生变化时，吸收塔浆液pH值具有较好的动态稳定以及较高稳态精度，将采取自优化模糊串级控制策略，如图3所示。采用梯度下降优化算法，实时采集满足条件的现场样本在线优化前馈参数，实现在锅炉的不同工况下，仍能够得到高精度的前馈量，采用模糊控制器替代外环PID控制器，并将前馈量作为模糊控制器输出量的尺度变换因子，得到供浆流量设定值，实现pH值的稳定、可靠。

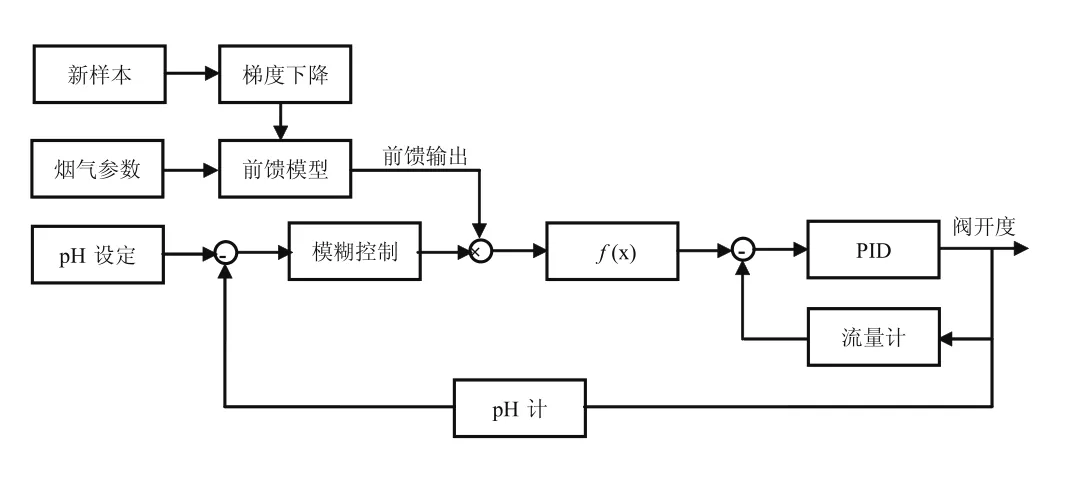
图3 自优化前馈-模糊串级控制

（1）梯度下降优化算法前馈的设计

梯度下降法是最常用、简单的最优算法，其利用当前位置的负导数方向作为搜索方向，该方向为当前位置的最快下降方向。当参数越接近目标值时，下降幅度越小，能够较准确找到模型的最优值。在获得多种机组工况下的样本后，通过梯度下降法优化算法获得最优的前馈模型参数，从而提高前馈输出的精度。梯度下降优化算法如下。

采集吸收塔浆液pH值的n个影响因素（如石灰石浆液密度、原烟气SO2浓度、原烟气流量等）及供浆流量，并记第j个影响因素的第i组数值为xij，供浆流量结合其量程换算成对应的供浆流量系数记为yi。

用m表示采集到的样本组数，利用梯度下降优化算法在线优化前馈模型的参数θ1，…，θn（θj指浆液pH值的第j个影响因素对应的前馈模型参数）。

前馈模型：

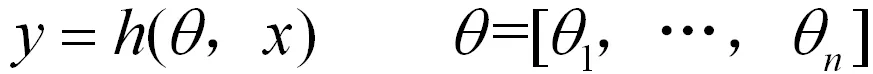
以供浆流量系数的值与前馈模型预测值之差的平方和作为损失函数：

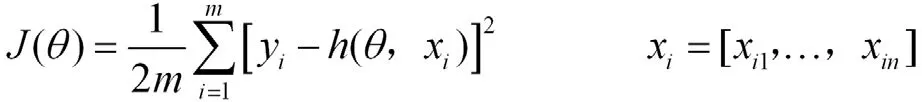
损失函数J(θ)对θ求导，即可得到下降最快的方向：

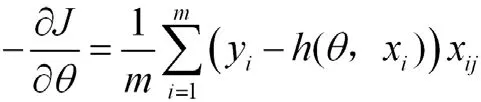
前馈模型参数θ沿下降最快方向的进行更新：

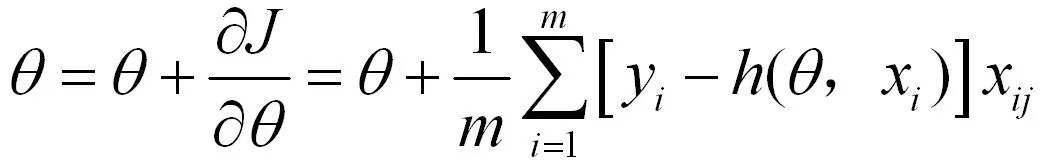
在线优化设定条件：若迭代次数大于100，则停止迭代计算；当迭代次数小于100时，若损失函数J(θ)存在最小值，且小于更新前损失函数J(θ)时，则将优化后的参数更新前馈模型。

（2）模糊控制器的设计

模糊控制是指利用模糊数学知识模仿人脑的思维对模糊的现象进行识别和判断，获得精确地控制量，实现自动控制。依据操作人员的经验，归纳出一套控制规则，根据系统运行过程的检测量，经过模糊化、模糊推理、解模糊等运算求出控制量，实现对被控对象的控制。

模糊控制依赖于操作人员经验获得的模糊规则，而无需建立过程数学模型，因此适用于非线性、强耦合时变、大滞后等特点的复杂控制系统。模糊控制器结构如图4所示。

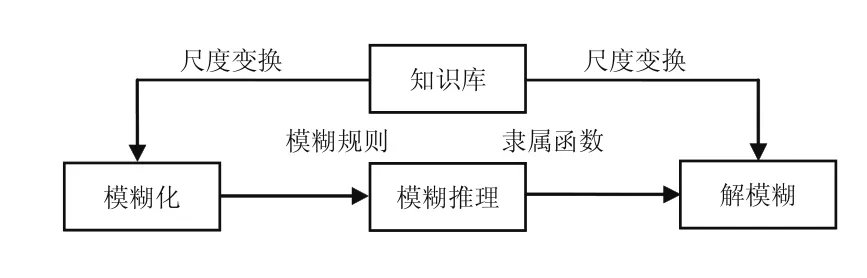
图4 模糊控制器的结构

1）模糊化是指将输入、输出的精确量转换为模糊量。具体过程如下：

确定模糊控制的两个输入量（一般为误差及误差变化率）及其值的变化范围，模糊控制器的输出量及其变化范围。记：

定义两个输入量和输出量的模糊论域如下所示，可以根据需要更改论域范围。

将以上的三个变量的论域分档，并定义其对应的模糊词集。

所有论域分7档：[-3 -2 -1 0 1 2 3]

所对应的模糊词集：{负大 负中 负小 零 正小 正中 正大}

符号表示模糊词集：{NB NM NS ZO PS PM PB}

2）知识库包括数据库和规则库两部分，其中数据库提供处理模糊数据的相关定义，如尺度变换因素、隶属函数等，而规则库则由一群语言控制规则描述的控制目标和策略，其可用模糊规则表来表示。

通常可根据输入或输出变量精确值的变化范围以及其对应的论域确定尺度变换因子。

隶属函数表达论域范围内的数值隶属于各模糊集的程度，应用最广泛的隶属函数为三角函数，如图5所示。

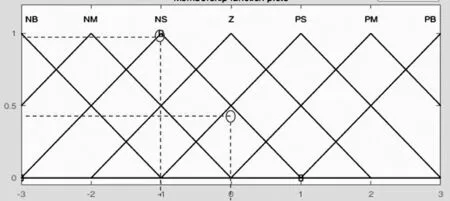
图5 隶属函数-三角函数

图5中NS的曲线图表示论域[-3，3]中各个值属于模糊集NS的程度，如值0属于模糊集NS的程度为0.5，值-1属于NS的隶属度为1。

模糊规则应体现操作人员的实践经验，通常模糊规则的制定依据以下两个原则，采用“if E and EC then U”形式的表述，由此便可得到模糊控制规则表，如表1所示。

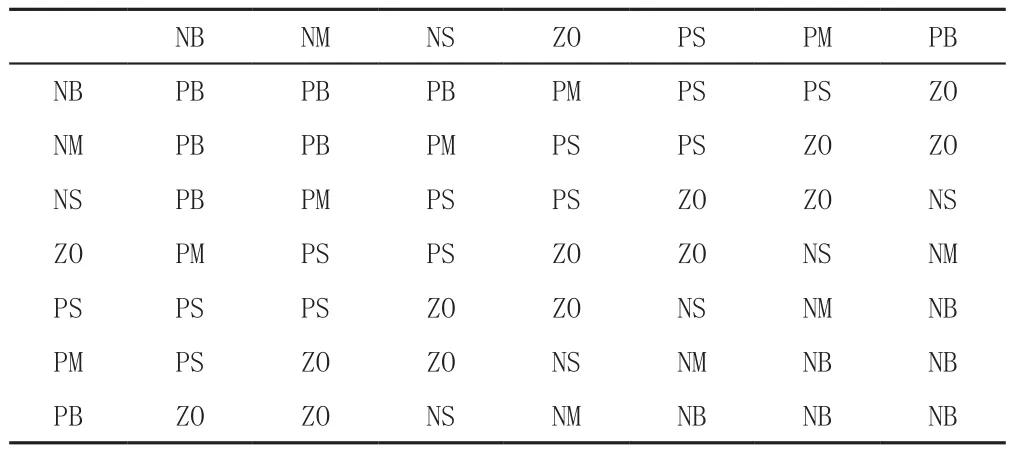
表1 模糊规则表

原则1：当误差大时，选择控制量以尽快消除误差为主。

原则2：当误差小时，选择控制量要注意防止超调，以系统的稳定性为主要出发点。

3）模糊推理是指由输入E和EC的值根据模糊规则表以及隶属函数计算获得模糊输出U的过程。由于现场对计算时间有较高的要求，因此采用模糊查询表的形式，如表2所示。表中为了兼顾模糊控制器的精度和反应速度，将模糊查询表中输入量的论域细分成12区域，得到的模糊查询表如下所示，若现场可以根据需要对论域进行重新划分，但最好不要少于6个区域。

4） 解模糊是指将模糊推理得到的输出量U，通过输出量的尺度变换因子转换为精确量，从而控制系统对象。

4 仿真及应用

4.1 模糊控制器的仿真

为了验证模糊控制器对于非线性、大滞后系统具有较好的控制效果，通过Matlab Simulink搭建系统进行仿真，并与PID控制器结果对比分析，如图6所示。吸收塔浆液pH值是具有滞后的被控对象，采用一阶惯性环节加一个滞后环节来描述[4]控制对象。

仿真系统中的模糊控制器控制规则采用表1，隶属函数为三角函数，选择增量型输出，以便更好地消除稳态误差。模糊控制器的尺度变换因子Ke=0.044、Kec=2、Ku=0.11、PID控制器的参数通过Matlab自整定得到，KP=0.1835、KI=0.0165、KD=-2.1081。系统的单位阶跃响应如图7所示。

表2 模糊查询表

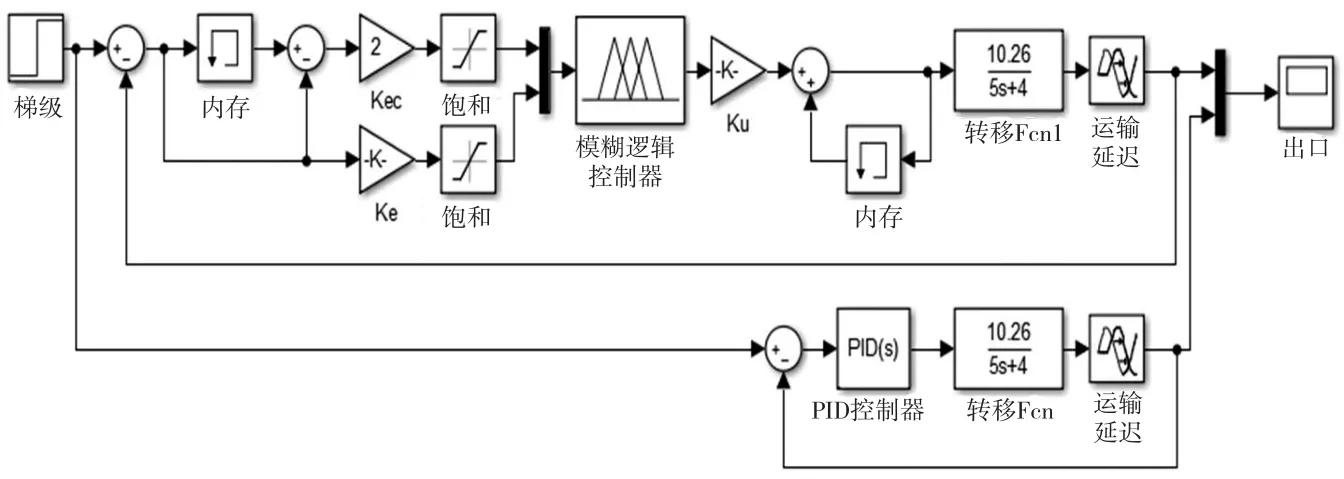
图6 模糊控制器与PID控制器的仿真框图

图7 模糊控制器与PID控制器的控制效果对比

由图7可知，增量型模糊控制器比常规的PID控制器具有较快的响应速度，较小的调节时间且无超调现象，验证了模糊控制器具有良好的控制效果。

4.2 模糊控制器参数的确定

模糊控制器的误差输入取吸收塔浆液pH设定值（取5.6）与测量值的差，并以吸收塔供浆流量设定值作为模糊控制器的输出。供浆流量调节阀仍采用PID控制器。根据现场测试，确定模糊控制器的参数见表3和表4。

4.3 工程应用

将现场调试确定的模糊控制器参数输入DCS控制系统，并应用于某电厂的脱硫吸收塔浆液pH值控制。该控制将原烟气SO2浓度、锅炉负荷、原烟气流量、石灰石浆液密度作为前馈预测主要影响因素、模糊控制器作为pH值控制器、常规PID进行供浆阀门的开度调节。它与常规前馈-串级控制运行效果对比如图8和图9所示。

图中机组负荷参量表示为烟气量、原烟气SO2浓度等相关的参数。从两图分析可知，采用常规前馈-串级控制时，随着机组负荷的变化，浆液pH值发生了较大的波动；采用自优化前馈模型结合具有专家经验的模糊串级控制的方案，在负荷变化时，仍然能够保持浆液pH值的稳定，并且随着前馈参数的持续优化，由负荷变化带来的波动将逐渐减小。

表3 PID控制器参数

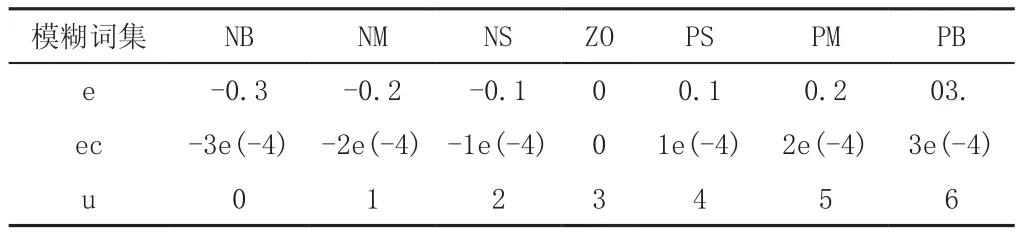
表4 模糊控制器参数

图8 常规前馈-串级控制效果

图9 自优化模糊串级控制效果

5 结语

通过实时采集的前馈数据样本，采用梯度下降优化算法在线优化前馈模型系数，使前馈模型具有较高预测精度，减少了调试工作量。经过仿真及工程应用验证，自优化模糊串级控制策略应用于大时滞、时变、非线性的pH值控制具有较小的超调量，能够提高pH值控制的稳定性，增强系统的鲁棒性和适应性。