桩板结构路基沉降计算方法及对既有桩基侧摩阻力的影响

，，

(1.中南大学 土木工程学院，湖南 长沙 410083；2.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081)

桩板结构可以提高路基的刚度和承载力，减少路基沉降，降低对既有桩基的影响，因此常常用于下穿既有高速铁路桥梁结构。有众多学者对桩板结构路基沉降进行了研究。在路基沉降方面，杨斌[1]研究了桩板结构技术在高速铁路施工中的应用，并现场观测桩板结构路基沉降，取得了较好的施工效果。沈宇鹏等[2]研究了桩板结构复合地基沉降特征，发现设置褥垫层可以提高桩间土固结度，减小沉降。荆志东等[3]通过离心试验研究了新型桩板结构路基沉降，发现钢筋混凝土承载板能有效减小路基沉降，使整体沉降更加均匀。Wang等[4]通过现场测试手段，研究了郑州—西安高速铁路桩板结构路基轨道板应力应变特征。李传宝等[5]通过物理模型试验研究了采空巷道上桩板结构路基沉降，发现桩基侧摩阻力沿深度减小，整体沉降量较小。Chen等[6]利用分层计算法和数值模拟法研究了软土地基桩板结构加固效果，发现桩板结构施工可以有效控制路基沉降。在桩板结构路基对既有桩基影响方面，代汉超等[7]通过有限元分析发现新建铁路桩板结构下穿既有京沪高速铁路对桥墩变形的影响较小。杨红春[8]通过数值模拟的方法，对比分析了桩板结构施工和普通路基结构施工对既有高速铁路桥墩变形的影响，发现桩板结构施工对既有高速铁路桥墩影响更小。

综上可见，对桩板结构路基沉降变形已开展了较多的数值模拟计算和试验研究工作，但是在沉降机理剖析和其对既有桩基侧摩阻力影响方面的研究相对匮乏。因此，本文根据Boussinesq理论提出桩板路基沉降计算解析解，并基于佐藤悟双折线模型得出桩板结构路基形式下既有桩基荷载传递曲线，结合工程案例进行验证。

1 桩板结构路基沉降计算方法

1.1 路基沉降组成

桩板结构路基由钢筋混凝土桩基、路基本体、钢筋混凝土承载板3部分组成，如图1所示。

图1 桩板结构路基示意

1.2 理论推导

在弹性半无限空间体内(见图2)，当其表面承受法向集中荷载F时，根据Boussinesq解可知极坐标下空间内任一点(ρ,R,z)的沉降量sz，即

(1)

式中：sz为z深度对应的沉降量；μ为泊松比；E为弹性模量；ρ为影响半径。

图2 弹性半无限空间

根据Boussinesq解对桩板结构路基沉降s1和s2分别进行计算。当桩基长度AB为L时，求得s1和s2分别为

(2)

桩板结构路基总沉降s(z)为

s(z)=s1+s2

(3)

2 既有桩基侧摩阻力分析

2.1 荷载传递函数

(4)

图3 双折线函数模型

根据佐藤悟荷载传递函数对桩板结构路基建立微分方程如下

(5)

式中：sp为桩身轴力；U为桩截面周长；A为桩截面面积；Ep为桩弹性模量。

将式(4)代入式(5)，求得微分方程的解为

(6)

式中：α2=Ucs/EpA；c1,c2均为待定系数。

根据文献[9]的求解方法，可求得式(6)中的待定系数c1,c2。

2.2 侧摩阻力分析

将式(3)代入式(6)可以求出sp沿深度方向z的分布spi。对桩单元受力分析(见图4)可以得到桩板结构路基沉降引起的既有桩基侧摩阻力公式，即

(7)

式中：d为桩的直径；Li为桩身分段长度；spi+1和spi分别为每段桩身顶部轴力和底部轴力。

图4 桩单元受力示意

3 算例分析

考虑桩板结构路基下穿高速铁路桥梁的工程背景，本文设计了3组算例，分别采用理论方法和数值计算方法计算桩板结构路基的沉降变形和既有桥梁桩基侧摩阻力，并将解析解与数值计算结果进行对比分析。

3.1 数值试验

图5 数值模型(单位：m)

表1 计算土体参数

注：γ2,c,φ分别为土体的密度、黏聚力、内摩擦角。

表2 既有桩基参数

注：Lp1,D1,γp1,Ep1,μp1,F分别为既有桩的长度、直径、密度、弹性模量、泊松比、桩顶荷载。

表3 不同工况下桩板结构路基参数

注：Lp2,D2,γp2,Ep2,μp2分别为桩板结构路基中桩的长度、直径、密度、弹性模量、泊松比；P为路基荷载。

图6 桩板结构中桩长对路基沉降的影响

3.2 沉降计算分析

桩板结构中桩长对路基沉降的影响如图6所示。可知，采用桩板结构施工可以降低路基整体沉降量，尤其可减小浅层路基土压缩沉降，且影响深度随着桩长的增加而增大，具体计算结果见表4。对比理论计算曲线和数值模拟曲线，可以将曲线分为3个区域：①桩板结构影响区域；②理论计算的路基沉降量偏小(绝对值)区域；③数值模拟的路基沉降量偏小区域。区域1中，理论计算曲线和数值模拟曲线基本吻合，说明理论计算和数值模拟均可以较好地反映桩板结构施工对路基沉降的影响。区域2中，理论计算的路基沉降量偏小，原因是理论计算时假设土体为弹性体，而弹性体在变形过程中没有能量损耗，因而不容易发生较大变形。但随着桩板结构中桩长的增加，理论计算和数值模拟计算的偏差逐渐减小，说明桩板结构施工可以增加浅层土体的弹性变形，弥补2种计算方法的偏差。区域3中，数值模拟的路基沉降量偏小，原因是本文模拟中z=0界面为位移边界，限制其进一步变形。

表4 既有桩基参数计算结果

3.3 既有桩基桩侧摩阻力分析

桩板结构中桩长对既有桩基桩身轴力和桩侧摩阻力的影响分别如图7和图8所示。

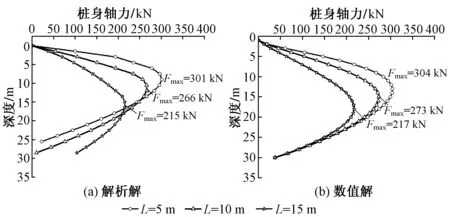
图7 桩板结构中桩长对既有桩基桩身轴力的影响

图8 桩板结构中桩长对既有桩基桩侧摩阻力的影响

由图7可知，桩板结构中桩体长度越大，既有桩基最大桩身轴力越小，且上部桩身轴力逐渐传递至桩中部和下部。由图8可知，随着桩板结构中桩体长度增加，既有桩基侧负摩阻力减小。这说明桩板结构路基可以减小对既有桩基的影响，且随着桩板结构中桩体长度的增加这种影响越明显。

图8对比了解析解和数值解，两者整体上吻合较好，但在浅层土体中两者有一定偏差。具体表现为：在浅层土体，理论计算求得的桩侧负摩阻力(绝对值)偏大。主要原因是靠近地表区域，在附加堆荷载作用下桩周土体主要受拉应力而下沉破坏，而理论计算时假设土体为弹性体，即抗拉强度和抗压强度相等，放大了土体的抗拉强度，造成理论计算求得的桩侧负摩阻力偏大。另外，与数值计算结果相比，理论计算求得的中性点位置较浅，见表5。主要原因是理论计算求得的浅层土体桩侧负摩阻力偏大，使得中性点往上浮。

表5 中性点位置

注：z1,z2分别为理论计算和数值模拟的中性点位置。

4 结论

1)基于Boussinesq沉降计算解，推导出桩板结构路基沉降计算解析解。结合佐藤悟双折线模型推导出桩板结构路基施工下既有桩基侧摩阻力计算公式。

2)排除边界效应的影响，利用桩板结构路基沉降计算解析解求得的路基沉降曲线，以及用桩基侧摩阻力计算公式求得的既有桩侧摩阻力变化曲线，与利用数值模拟求得的两类曲线基本吻合，且吻合度随着桩板结构中桩长的增加而增加。

3)理论计算和数值模拟结果均表明，桩板结构路基可以有效地将地表荷载传入地基深部，减小路基表面沉降，减小既有桩基桩侧负摩阻力。