一种基于关键度评估的地铁信号设备维护方法

莫志刚， 骆汉宾

(华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

地铁信号系统的维护模式分为计划修、状态修、事后修，前两种模式属于预防性维护，如图1所示。根据设备的重要性与故障率，计划修又分日巡视，日检、双周检、月检等不同的等级，如何将繁多复杂的信号系统设备分类，并使之与设备的维护模式相适应，本节提出基于信号设备综合关键度的分类方法。

图1 地铁信号系统维护作业模式

评价地铁信号系统设备的综合关键度主要从三个维度出发，一是设备故障后影响行车安全风险的关键度；二是设备故障后影响行车服务可靠性的关键度；三是影响系统维护费用的关键度。信号CBTC(Communication Based Train Control)系统的DCS(Data Communication System)子系统、ATS(Automatic Train Operation)子系统的设备故障后仅仅存在影响行车服务度、维护费用的风险，CBI(Computer Based Interlocking)子系统的设备故障后可能同时影响行车安全、服务可靠性与维护费用的风险。

通过分析信号CBI子系统设备对行车的安全风险影响度及列车服务可靠性、其本身的故障概率、故障检测难度、故障定位难度、故障维护难度、维护恢复时间、维护价值8个方面三个维度及设备本身可维护性的影响，综合评估设备的关键度。为信号系统设备运营维护模式的分类提供了一种新的思路。

1 基于模糊层次分析法(AHP)评估模型的构建

层次分析法(Analytic Hierarchy Process，AHP)是一种综合评估方法，结合问题的定性分析、定量分析方法[1～3]，综合人的主观经验和客观数据，建立有序的递阶结构，通过层层分解得到的各级影响问题的因素，解决目标层复杂决策问题。

常规层次分析法常为3层结构，一般由目标层、准则层和元素层，各层之间的关系可用框图及连线表示。目标层是层次结构模型需要实现的最终目标，中间层是为实现最终目标采取的某种方法、原理等，中间层可以根据需要添加到多层；与准则层对应的多项因素元素层是解决问题的最基本单元。建立AHP层次结构模型，关键在于如何通过判断矩阵得到各指标的排序权重，确定同一层各元素的相互重要性的比较。采用Saaty设计的九级标度判别法表征同一层两个元素之间的重要程度，判断矩阵一致性计算用于检验判断矩阵是否合理[4,5]。

传统分析方法存在以下问题：

(1)信息采集来源复杂，受测评专家意见的主观性影响；

(2)公式CR=CI/RI，CI(Coincidence Indicator)为一致性指标，CR(Consistency Ratio)为一致性比率，RI(Average Random Consistency Index)为平均随机一致性指标)计算判断矩阵的一致性，且当CR≤0.1时，判断矩阵一致性合理，但随着中间层次的增加与底层元素的增多，判断矩阵的一致性计算变得非常复杂，检验难度也随之增大，需要重新调研、收集及分析数据，导致多次重复构造判断矩阵；

(3)判断矩阵一致性检验可以检查专家对同1个元素前后判断的一致性，但无法确保专家打分与实际情况是否相同。

下面为基于模糊理论的评估专家打分改进方法及示例：

构建1个论域U，γ，δ为论域U上的两个对象集。γ，δ在U上的划分分别为α={α1,α2,…,αm}和β={β1,β2,…,βn}，α为指标因素属性集，β为状态属性集。

根据香农信息论熵的定义[6]，H(γ)可表示为：

(1)

式中：p(·)为条件概率。

结论属性集β相对于因素属性集α的信息关联程度可以用一个条件概率H(β/α)表示。依据香农信息论中熵的概念[7]，可用以下公式确定：

(2)

H(β/α)表征因果关系的两者之间信息关联程度影响修正因子，引入到层次分析法中底层元素影响准则层关键度的公式表达中。轨道交通行车指挥系统中信号系统分布在车载、轨旁、车辆段、车站及指挥中心，子系统繁杂且相互关联，引起信号CBTC失效的故障信息类型多，组合形式复杂，采集的数据具有随机性和模糊性，与传统的层次分析数选用评估指标体系不同，因组件的故障对CBTC失效影响程度不一致，仅仅分析故障率不足以评估组件关键度。

从安全性影响度、可维护性、维护成本、维护时间、故障率、列车服务可靠度、故障检测难度等8个方面综合评估影响CBTC几大子系统，专家根据组件的故障监测数据、维护记录及评分等级表分类对应信息对CBI子系统的关键组件及8个底层因素权值进行打分，专家打分乘以权值及信息修正因子H(β/α)，计算关键子系统重要度。由于各项指标的标度类型和量纲都不同，为便于不同类型与量纲数据之间的比较，需要对评估指标进行规一化、规范化处理，先根据信号系统构架构建评估对象的指标体系，对指标数据预处理。

提出运用数据粗糙集理论知识对专家对权值的打分进行预处理，结合模糊数学理论计算各元素指标的重要性与权重系数，减少测评专家的主观性影响，确保通过判断矩阵的一致性检验[8,9]。基于粗糙集的关键组件评估流程如图2所示。

图2 基于粗糙集的关键组件评估流程

采用统计粗糙集理论属性重要性方法确定各指标的重要性及权重因子[10]，对8大评价指标模糊化处理，将其分为5个等级分别为：[0.00，0.20)，[0.20，0.40)，[0.40，0.60)，[0.60，0.80)，[0.80，1.00]，对应0.1，0.3，0.5，0.7，0.9。条件属性集设置为α={α1,α2,…,αm}，状态属性集设置为β={β1,β2,…,βn}。

在层次分析法中，因最底层的各因素相关倒数第2层组件的影响不完全一致，而且每位专家对同1个组件对应的底层各因素(故障率、安全影响度、服务可靠度、维护成本、维护时间、维护价值、维护影响度、故障检测难度)的影响认知度也不完全相同。如由第i个专家针对CBI中的转辙机的底层各元素打分，再进行模糊化(见表1)，得到底层元素的权值ωi，总共有多个专家参与打分，依次可以计算各位专家的打分得到底层元素的权值(ω1,ω2,…,ωi…,ωj,…)，如所有专家的判断矩阵都能通过一致性检验，通过求平均数得出底层元素的权值ω。

表1 一致性校验指标

第i位专家的判断矩阵为：

根据Matlab仿真计算得到矩阵的最大特征根为λmax=8.1403。对应的特征向量归一化计算得：ωi=[0.1523, 0.0971, 0.1937, 0.0555, 0.2445, 0.1615, 0.0263, 0.0691]。根据CI =(λmax-n)/(n-1)，CR=CI/RI及表1中对应的RI值得：CI=0.0200，CR=0.0142。模糊化后第i位专家的判断矩阵为：

根据Matlab仿真计算得到矩阵的最大特征根为λmax=8.0090。对应的特征向量为归一化计算得：ωi=[0.1363, 0.1363, 0.2273, 0.0455, 0.2273, 0.1363, 0.0455, 0.0455]。根据CI =(λmax-n)/(n-1)，CR=CI/RI及表1中对应的RI值得：CI=0.0013，CR=0.0009<0.1。

由此可看出，模糊化后的判断矩阵更容易通过一致性检测，专家的判断更科学合理。

2 基于粗糙集理论属性联锁组件关键度的计算

因影响功能部件关键度打分的评价因子有定量与定性两类，为使评价因子可计算，需要将评价因子的各类指标量化。参考行业相关标准，可将量化水平指标L(Level)分为5级(L1～L5)，每级评价指标对应定量数据或不同程度的定性描述。

专家根据故障、维护、运营服务延时等记录对CBI系统中的8个主要功能部件进行评价等级评估打分(表2)，CBI的8个主要功能部件的关键度计算公式如式3。

C=Si评价因子Wi权值H(β/α)

(3)

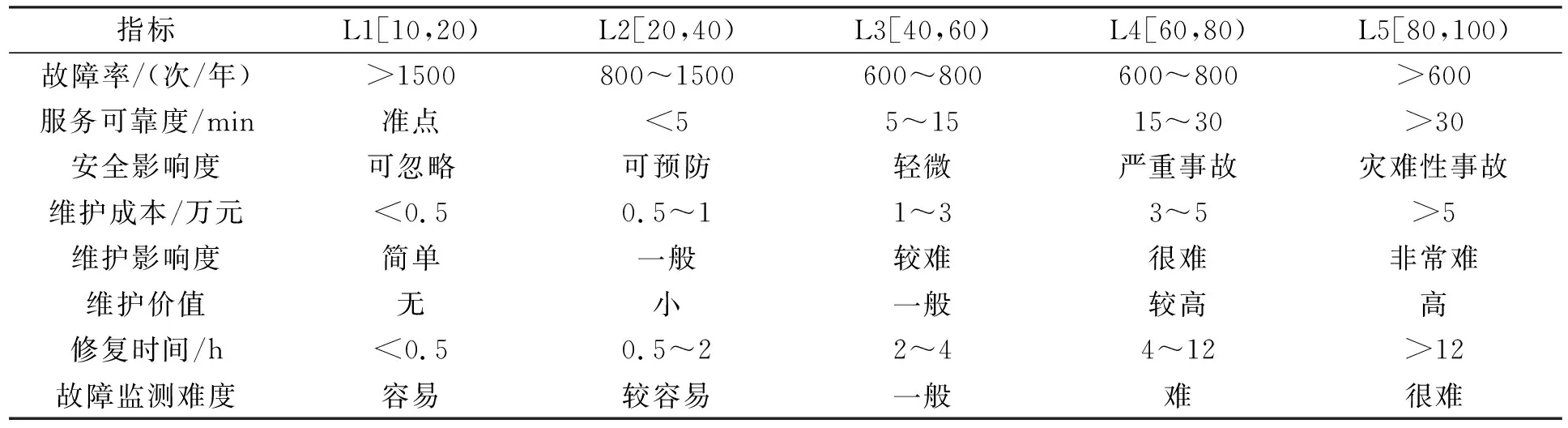
表2 评估等级打分表

CBI组件关键度评分见表3，CBI子系统中组件的关键度排序为：转辙机>道岔>信号机>电缆>计轴>接地装置>站台门。同理，可计算信号其他子系统设备的关键度。综合关键度可以按一定的数字范围划分等级，每个等级对应不同的设备维护模式。参照以可靠性为目标的设备主动维护模式RCM规则，运营维护人员可按一定的规则与综合关键度数值大小划分综合关键度等级，信号设备组件的维护模式与设备组件综合关键度等级相对应。

表3 CBI组件关键度评分

3 结 语

本文研究的综合关键度划分设备维护模式为地铁信号设备维护管理提供了一个定性的分析方法。从信号系统可维护角度，构建模糊层次分析法模型计算信号联锁子系统部分组件的关键度，判断矩阵通过了一致性检验，验证了模型构建的合理性，排序结果表明，设备组件的关键度排序与其故障率大小并不存在一一对应关系，还应结合考虑信号设备对行车的安全性影响度及列车服务可靠度、维护价值、维护成本、维护时间、故障检测难度等因素。此结论对信号设备日常保养维护方法有一定的参考意义。