斜向往复荷载作用下方钢管混凝土柱的抗震性能及损伤分析

周 理， 苏益声， 江 兰

(1. 广西大学 土木建筑工程学院， 广西 南宁 530004； 2. 贵州大学 建筑与城市规划学院， 贵州 贵阳 550003)

方钢管混凝土是在钢管中填充混凝土而形成的一类组合构件，它具有承载力高、塑性及韧性好、施工便利及耐火性能较好等诸多优点，因此在高层建筑及桥梁工程中具有广泛应用[1]。目前，针对方钢管混凝土柱的抗震性能研究已较为深入。Sakino与Tomii[2]对径厚比(D/t)在24～34之间的方钢管混凝土柱进行拟静力试验研究，结果表明：在管内混凝土压馈后，钢管壁出现局部屈曲，并对构件的承载力产生不利影响；Inai等[3]对20根方钢管混凝土柱进行往复荷载试验研究，分析了宽厚比、材料强度、轴压力类型和加载方向对构件承载力及滞回性能的影响。国内对方钢管混凝土柱抗震性能的研究起步较晚，吕西林等[4]进行了12根方钢管混凝土柱的低周往复荷载试验，对轴压比、宽厚比及内填混凝土强度等影响参数进行了较为详尽的研究，结果表明方钢管混凝土柱具有良好的抗震性能；徐培蓁等[5,6]对6根足尺比例的方钢管混凝土柱进行抗震性能试验研究，分析了含钢率、长细比及轴压比等参数的影响；此外，文献[7,8]也报道了方钢管混凝土柱的抗震性能试验研究成果。

上述有关方钢管混凝土柱抗震性能的研究成果主要基于地震作用方向与构件截面的轴对称方向一致，但在实际工程中，地震作用于建筑物的方向是随机的，纵使设计时在规定地震作用方向下，也往往会由于斜交的结构布置方案、刚度不对称等因素造成构件的实际运动方向与截面轴对称方向不同。针对斜向荷载作用下普通钢筋混凝土柱的研究成果表明：当作用力方向改变时，构件的承载能力、破坏模式及抗震性能均会出现不同程度的变化[9]。鉴于以上原因，本文对斜向荷载作用下的方钢管混凝土柱进行研究，分析构件的抗震性能及损伤状况，研究成果可为实际工程应用提供参考。

1 本构模型的建立与验证

采用有限元程序ABAQUS建立数值分析模型，方钢管及核心区混凝土均采用C3D8R三维实体单元，钢管与混凝土界面的黏结滑移力学行为采用基于库伦理论的切向力模型，界面摩擦系数根据文献[10]的建议取为0.5。

1.1 钢材本构关系

钢材的应力-应变关系采用文献[1]所建议的双折线模型，如图1(图中：fy，fu分别为钢材的屈服强度及极限强度；εy，εu分别为钢材的屈服应变及极限应变)所示，即包括弹性阶段与强化阶段，其中强化阶段的变形模量取为：

Ep=0.01Es

(1)

式中：Ep为方钢管强化阶段的变形模量；Es为方钢管的弹性模量。本文数值分析时弹性模量取为2.06×105N/mm2，泊松比取0.3。采用Mises屈服准则及相关联流动法则来描述钢材的塑性变形。

图1 钢材的应力-应变关系

1.2 核心区混凝土本构关系

方钢管核心区混凝土的受压应力-应变关系采用文献[1]所建议的模型，其曲线方程表述为：

(2)

(3)

(4)

(5)

(6)

(7)

式中：fc为混凝土轴心抗压强度；fy为钢材屈服强度；Ac，As分别为混凝土及钢管的截面面积；ξ为套箍系数。

混凝土的受拉本构关系采用文献[11]所建议的本构方程，其表达式为：

(8)

式中：x=ε/εt；y=σ/ft；ft为混凝土轴心抗拉强度；εt为与ft相对应的应变；α为曲线下降段参数。

1.3 本构模型验证

选取课题组前期试验所得的方钢管混凝土柱数据，其中方钢管的截面尺寸为120.1 mm×5.52 mm，钢材的屈服强度为360.29 MPa，极限强度为486.99 MPa，弹性模量为2.36×105MPa，泊松比为0.28；混凝土材料的轴心抗压强度为32.26 N/mm2，轴心抗拉强度为2.6 N/mm2；试件长度为860 mm。图2为该试件的试验滞回曲线及有限元分析滞回曲线对比，表1为重要特征参数的有限元计算与试验测试对比分析结果。由图2及表1可见，试验与有限元模拟所得到的滞回曲线及相关特征参数吻合较好，表明数值模拟所选用的本构模型是合理的。

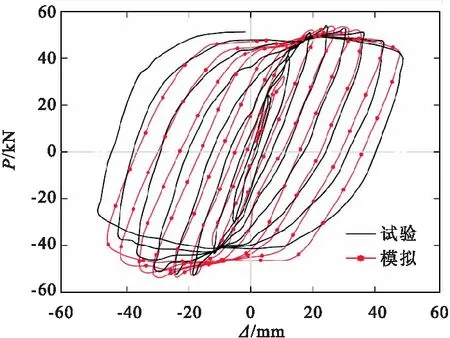
图2 滞回曲线对比

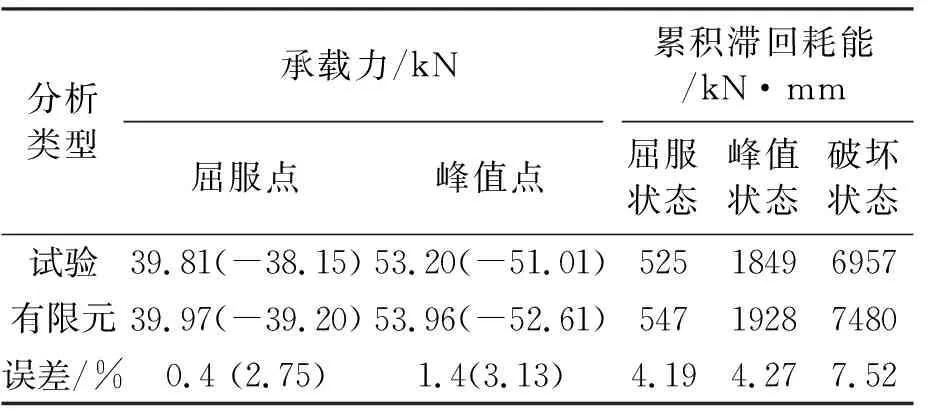
分析类型承载力/kN累积滞回耗能/kN·mm屈服点峰值点屈服状态峰值状态破坏状态试验39.81(-38.15)53.20(-51.01)52518496957有限元39.97(-39.20)53.96(-52.61)54719287480误差/%0.4 (2.75)1.4(3.13)4.194.277.52

注：括号内的数字为负向承载力

2 数值分析模型

考虑套箍系数、轴压比、加载方向三个变量参数，共设计了12个数值分析模型。方钢管采用120 mm×3 mm及120 mm×5 mm两种规格，材质为Q345级，其屈服强度为345 MPa，极限强度为470 MPa，弹性模量为2.06×105MPa；所有模型混凝土均采用C40级，其轴心抗压强度为26.8 N/mm2，轴心抗拉强度为2.39 N/mm2，弹性模量为3.25×104MPa。各模型水平加载点距支座距离为480 mm，如图3a所示；水平加载角度分别取0°，15°，30°，45°，如图3b所示。各模型的设计参数详见表2 ，表2中套箍系数按式(9)进行计算，轴压比按式(10)进行计算。

ξ=fyAs/fckAc

(9)

(10)

式中：fy为钢材的屈服强度；fck为混凝土的轴心抗压强度；N为施加于各模型上的轴压力。模型轴压比分别取0.3，0.6，在考虑荷载分项系数及材料强度分项系数后，相当于特一级框架柱与四级框架柱的轴压比限值要求。

所有模型均采用位移控制的加载制度。经分析，各模型的屈服位移接近5 mm，为便于比较，统一将Δy=5 mm定为各试件的屈服位移，模型屈服前，分别以0.2Δy，0.4Δy，0.6Δy，0.8Δy的位移控制水平各循环加载一次；模型屈服后，以Δy的倍数为位移控制水平，每级循环加载一次直至试件破坏。

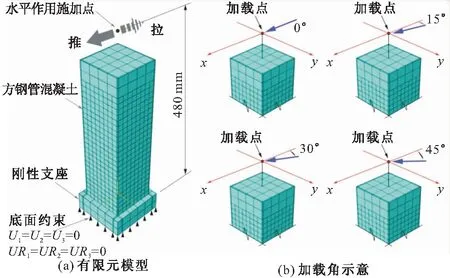
图3 模型加载示意

模型编号方钢管b×t/mm×mm套箍系数ξ轴压比n加载角度θ/(°)120×3-0.3-0120×31.390.30120×3-0.3-15120×31.390.315120×3-0.3-30120×31.390.330120×3-0.3-45120×31.390.345120×5-0.3-0120×52.450.30120×5-0.3-15120×52.450.315120×5-0.3-30120×52.450.330120×5-0.3-45120×52.450.345120×3-0.6-0120×31.390.60120×3-0.6-15120×31.390.615120×3-0.6-30120×31.390.630120×3-0.6-45120×31.390.645

注：模型编号的前2位数字为方钢管的边长与壁厚，第3位数字为轴压比，第4位数字为加载角度

3 抗震性能分析

3.1 滞回曲线

所有模型的滞回曲线如图4所示。由图可见：(1)所有模型的滞回曲线均较饱满，呈纺锤形，表明构件具有良好的延性及耗能能力；(2)对同条件(同轴压比及套箍系数)的构件来说，滞回曲线随着加载角度的增加其捏拢效应会更加明显，表明构件的耗能能力会因加载角度的增加而降低；(3)在不同轴压条件下，构件的滞回曲线差异明显，说明轴压比是影响构件滞回曲线的核心因素之一。

图4 滞回曲线

3.2 骨架曲线

图5给出了构件从屈服点到破坏点之间的骨架曲线。从图中可以看出，当加载角度增加时，屈服点、极限点及破坏点的承载力均有不同程度的降低。对于套箍系数为1.39，轴压比为0.3的试件，当加载角度为45°时，其正向极限承载能力相比0°加载的构件降低了9.2%，负向极限承载能力降低了6.1%。维持轴压比0.3不变，而构件套箍系数提高至2.45时，改变加载角度，构件的最大正向与负向极限承载能力分别降低了10.7%与10.4%。保持套箍系数1.39不变，提高轴压比至0.6，此时改变加载角度，构件的最大正向与负向极限承载能力分别降低了9.7%与12.5%。图6给出了极限承载力随加载角度改变的降低比。从图中可以看出，承载力降低值并非随加载角度的改变而呈线性变化。为方便实际工程应用，可按加载角度每增加10°，承载力降低2.333%来近似考虑。

图5 骨架曲线

图6 极限承载力降低量-加载角度关系

3.3 延性系数

延性性能是结构抗震的重要指标，其反应构件从屈服到破坏状态的变形能力，通常采用延性系数来表征这一特性。将试件破坏时的柱顶极限位移Δu与屈服位移Δy之比定义为位移延性系数μ。图7给出了正负向平均位移延性系数μ随加载角度改变的变化图。从图中可以看出，加载角度对位移延性系数的影响并不明显，套箍系数的影响略大，而轴压比的大小则是影响构件位移延性系数的核心因素。

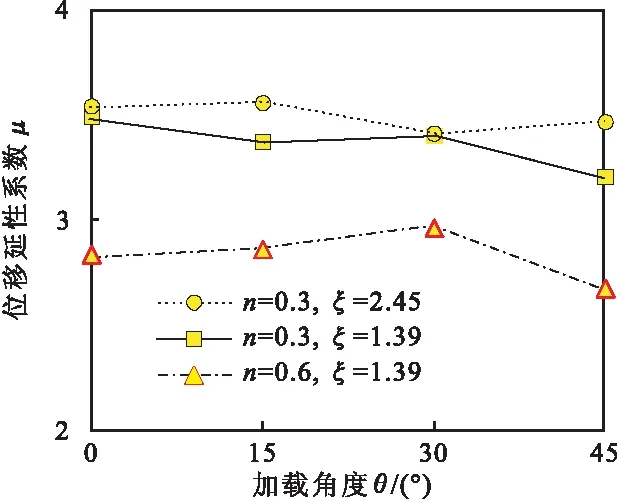
图7 延性系数-加载角度关系

3.4 耗能能力

用累积滞回耗能来反应构件的能量耗散能力。图8反应了同轴压比、同套箍系数的各类构件当加载角度不同时的能量耗散情况。由图可知：(1)同条件的各类构件(同轴压比、同套箍系数)，当加载角度增大时，构件的累积滞回耗能均有不同程度的降低。如n=0.3，ξ=1.39时，45°加载构件在破坏状态时的累积滞回耗能只有0°加载构件的81.4%；当n=0.3，ξ=2.45时，此值约为80.3%；对于n=0.6，ξ=1.39的构件，此值仅为75.9%。以上分析表明，加载角度对构件耗能能力影响明显。(2)构件在达到极限承载力以前，加载角度对累积滞回耗能影响不大，超过极限承载力后，加载角度对构件滞回耗能的影响明显增大，而且随着水平位移值的增加，这种影响所带来的差异越显著。

图8 累积滞回耗能

3.5 应力分析

当n=0.3，ξ=1.39时，钢管与核心区混凝土在峰值状态下的应力云图如图9所示，峰值状态下钢管的纵向应力值如图10所示。从图中可以看出：方钢管与混凝土的截面中和轴基本保持一致，表明在峰值状态下，方钢管与混凝土协同工作良好；截面中和轴与荷载加载方向基本保持垂直，并未因加载方向改变而产生变化；方钢管角部应力值略小于垂直边应力值，表明钢管角部变形受混凝土约束较高，峰值状态下，受压边与受拉边的钢管应力值大小基本相等，均已超过材料屈服强度，约为材料屈服强度的1.1倍。

图9 峰值状态下的应力云图

图10 极限状态下钢管的竖向应力值/MPa

3.6 破坏模式

以轴压比为0.3、套箍系数为1.39的方钢管混凝土柱为例，分析不同加载角度下构件的破坏全过程。图11(y为屈服点，p为极限点，u为破坏点)为各模型特征点的累积塑性应变，图12为各模型累积塑性应变的变化趋势。从图中可以看出：(1)不同加载角度对方钢管混凝土柱的塑性铰长度影响不大，均约为1倍截面边长；(2)不同加载角度下，各模型的破坏形态均为局部压屈破坏，但钢管鼓曲的程度不同，加载角度越大，鼓曲越显著；(3)累积塑性应变随加载角度的增加而增加，当加载角超过30°后，累积塑性应变基本趋于稳定。

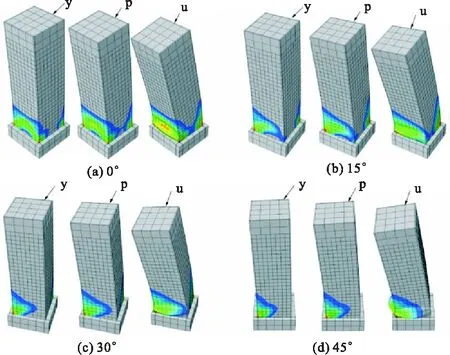
图11 各特征点的累积塑性应变

图12 累积塑性应变变化趋势

4 损伤评估

构件在地震作用下的损伤程度反应了结构的抗震性能，合理地评估地震作用下结构的损伤程度是结构性能设计的重要依据。Park-Ang模型能够同时考虑构件最大变形与结构滞回耗能两方面的影响，被广泛用于地震损伤评价[12]。Park-Ang模型的震害指数表述如下：

(11)

β=(-0.447+0.073λ+0.24n+0.314ρl)0.7ρv

(12)

式中：λ为构件剪跨比；n为轴压比；ρl为纵向钢筋配筋率；ρv为构件体积配箍率。

根据文献[1,13]给定的钢管约束混凝土本构模型，钢管的环向及纵向应力可根据式(13)～(16)进行计算，由此可分解出钢管纵向及环向的等效作用效应用于换算ρl及ρv。

(13)

(14)

(15)

(16)

式中：b，t分别为钢管的边长及壁厚；fyl，fyv分别为钢管的纵向及环向应力；fr为混凝土侧压力。通过作用效应等效，ρl及ρv可按以下公式进行计算。

(17)

(18)

利用Park-Ang模型进行构件损伤指数计算，结果如图13所示。从图中可以得出以下结论：(1)加载方向对方钢管混凝土的地震损伤指数影响不明显；(2)轴压比及套箍系数对构件损伤指数影响较大，这反应出轴压比及套箍系数是影响方钢管混凝土柱抗震性能的核心因素；(3)轴压比为0.6时，构件破坏状态下的损伤指数在1.1～1.3之间，超出了震害指数的原始定义限值，表明模型的收敛性还有待进一步改进。

图13 模型损伤指数

5 结 论

本文通过有限元数值模拟，分析了不同轴压比及套箍系数条件下，加载角度对方钢管混凝土柱抗震性能的影响，并利用Park-Ang模型计算了地震损伤指数。根据分析得出以下主要结论：

(1)加载角度对构件滞回曲线有一定程度影响。随着加载角度的增加，滞回曲线捏拢效应会更加明显，表明构件的耗能能力在降低，累积滞回耗能分析结果显示：当加载角度增加至45°时，构件的累积滞回耗能降低约20%。

(2)加载角度对构件的极限承载力有影响，但不显著。当加载角度增加至45°时，极限承载能力降低约10%。经拟合，可大致按加载角度每增加10°，极限承载力降低2.333%进行近似考虑。

(3)不同加载角度下，方钢管混凝土柱的塑性铰长度基本一致，均为1倍截面边长；各模型破坏形式均为局部压屈破坏，但加载角越大，钢管鼓曲越显著。

(4)利用Park-Ang模型计算方钢管混凝土柱的地震损伤指数，结果表明加载角度不是影响损伤指数的关键因素，轴压比及套箍系数对损伤指数影响较大，这反应出轴压比及套箍系数是影响方钢管混凝土柱抗震性能的核心因素。