无蒙皮复合材料网格结构设计与分析
提亚峰 刘利明 陈献平 季宝锋 黄 诚
(北京宇航系统工程研究所,北京 100076)
0 引言
复合材料网格结构以其优异的力学承载性能及诸多工艺生产方面的优点在航空航天领域得到了越来越广泛的应用。无蒙皮复合材料网格结构在继承复合材料网格结构自稳定性高、抗屈曲能力强、可优化性强、初始缺陷敏感性低、应力分布均匀、可有效分配载荷、便于检测修补、可自动化制造、制造成本低、生产效率高等诸多优点[1]的同时,还有自身独特的优点:计算及试验均表明复合材料网格结构中网格筋条承载效率远高于蒙皮[2-3];无蒙皮复合材料网格结构通过成型网格筋条的方法,实现结构轻质化。网格结构网格筋条与蒙皮间的粘接界面是薄弱界面,无蒙皮复合材料网格结构自然克服了这一缺点,提高结构承载能力。由于无蒙皮复合材料网格结构无法通过蒙皮传递剪切力,有些网格形式不适合设计成无蒙皮复合材料网格结构,要有针对性地进行网格形式选择。同时由于没有蒙皮,网格筋条相交的节点处成型及网格筋条与端框的连接均更为困难。目前国内尚无自主设计生产的无蒙皮复合材料网格结构应用于工程实践。
本文以工程应用为目的,通过适当的设计成型方法克服无蒙皮复合材料网格结构设计成型等困难,以代替金属杆系结构,实现结构低成本、轻质化。
1 无蒙皮复合材料网格结构设计思路
无蒙皮复合材料网格结构可优化性强,其优化变量包括网格螺旋筋的螺旋角角度和螺旋筋数目、纵筋和环筋的数目、筋的截面尺寸如筋条高度和宽度等。在结构外形尺寸及载荷一定的条件下,对设计变量进行优化,可得到质量最轻的结构。但在结构可优化性强的同时,也加大了结构优化难度。为使结构均匀承载,要求螺旋筋数等分圆周且对称、筋条高度是单层丝束厚度的倍数。即这两个变量是离散变量。筋条宽度由丝束宽度决定,可任意调整,即此变量是连续变量。能够在火箭结构中得到工程应用的无蒙皮复合材料网格结构,其承载要求高且承载形式复杂。承载能力计算涉及非线性。因此无蒙皮复合材料网格结构优化是多变量(包括连续和离散混合变量)、多约束、多工况和非线性优化。由于复合材料结构设计-材料-工艺三者密不可分,其工艺特点是零件制造和材料成型同时完成,工艺成型质量决定结构承载能力,同时筋宽、筋高比也受到工艺限制。结构设计及优化必须考虑工艺可行性和简便性。以工程应用为目的,考虑工艺成型问题,定性与定量分析相结合,分级优化,最终达到设计、计算、优化、工艺等各方面综合最优的效果;而不是仅追求理论计算承载最高、结构质量最轻。根据这一设计思路,应先进行无蒙皮复合材料网格结构网格形式选择;再对此网格形式中的几个典型结构进行计算及选择;以工程上可行的参数组合为基础进行有限元优化计算;确定工程方案并进行设计生产试验验证,在确保满足工程应用的前提下为进一步优化创造条件。
2 无蒙皮复合材料网格结构网格形式选择
无蒙皮复合材料网格结构主要有菱形(含斜置正交)、长方形(正置正交)、六边形、三角形、三角形与六边形相间构型(混合三角形)、米字形等网格形式可供选择,如图1所示。
菱形、长方形复合材料网格结构为双向筋条结构。长方形复合材料网格结构没有斜向螺旋筋条,抗扭能力差;菱形复合材料网格结构没有环向筋条,环向刚度差。这两种网格形式均不适合设计成无蒙皮结构。六边形、三角形、三角形与六边形相间构型复合材料网格结构为三向筋条结构。六边形构型各向筋条均不连续,承载能力差且工艺上不易成型。三角形网格结构是一种很好的结构形式,其环筋、纵筋和斜筋(螺旋筋),三向筋条构成柱面三角形框架,是一种较为稳定的结构。合理设计的三角形网格结构具有自稳定性。此特点对于提高无蒙皮结构承载能力尤其重要。同时三角网格结构环筋、螺旋筋缠绕成型工艺性好,生产效率高[3]。但三角形网格结构在任何一节点上都有三条筋相互交叉,存在架空现象[1]。此工艺困难对无蒙皮复合材料网格结构尤为难以克服。因此三角形网格不适合设计成无蒙皮结构。三角形与六边形相间构型复合材料网格结构拥有三角形网格结构的优点,同时由于其任意节点都是两向筋条向交叉,克服了三角网格的工艺成型困难,因此适合设计成无蒙皮结构。

图1 无蒙皮复合材料网格结构网格Fig.1 Grid forms of composite materials
米字形复合材料网格结构为四向筋条结构,是在三角网格的基础上增加了轴向承载效率最高的纵向筋条,能承受轴、弯、剪、扭等各种载荷,是最为稳定的无蒙皮网格结构。但四条筋相互交叉,架空现象更为严重,因此也不适合设计成无蒙皮结构。
综上所述,三角形与六边形相间构型是无蒙皮复合材料网格结构优选构型。
3 无蒙皮复合材料网格结构设计、计算及优化
3.1 轴压承载能力计算公式
无蒙皮复合材料网格结构的设计计算,可参照复合材料网格结构的设计计算方法,不计及蒙皮承载能力即可,相关公式如下[4]:
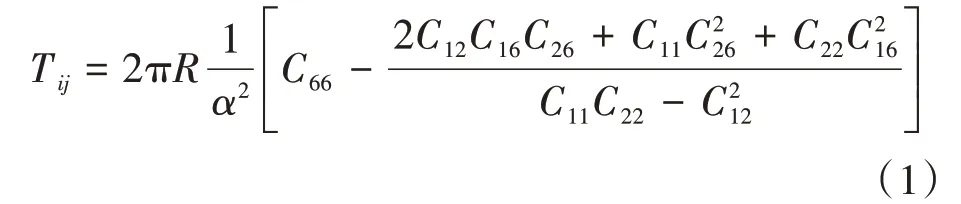
式中,Tlj为临界轴压承载能力。


式中,l1为网格加筋壳长度,R 为网格加筋壳半径,m为加筋壳失稳后的纵向半波数,n为加筋壳失稳后的环向波数;Aij为拉伸刚度,Bij为拉-弯耦合刚度,Dij为弯曲刚度。

规定筒壳轴线x正向到层坯主方向1的夹角θ为层坯的主方向,则层坯在壳体结构主方向上的应力-应变关系为:

式中,Q11,...,Q66为在层坯主方向坐标系里的刚度元素。
设单向纤维正交各向异性层坯在其主方向的性能为E1、E2、ν12、G12。正交异性各向层坯在其主方向上的应力-应变关系为:

对于筋条部分,设某一方向的筋条宽度为b、高度为h、间距为s,顺纤维方向的弹性模量为E,则这同一方向的筋条构成一当量正交异性层。其当量正交异性层的方向角为筋条的方向角θ,此正交各向异性层的弹性常数变为

3.2 典型结构的计算
圆柱形、三角形与六边形相间的无蒙皮复合材料网格结构在确定直径D 和长度L 后,共有6 个参数(图2)需要确定:筋条高度h;螺旋筋的螺旋角φ(θ);螺旋筋宽度δh(b 螺旋);环筋宽度δc(b 环);螺旋筋间距ah(展开尺寸s螺旋);环筋的间距ac(s环)。ah与同高度两相临螺旋筋节点间周向弧长a之间的关系为:ah= a cos φ,a 可表示为度数,如6°即表示占圆周的1/60。ac= akcsc φ/2,即当螺旋角φ 及螺旋筋的间距ah确定后,环筋的间距ac随之确定。即共有5个参数供优化。先确定a,再通过a 与ah及ac与ah之间的关系式确定ah及ac,如此便于螺旋筋等分圆周。3.1 节的公式中含有以上复合材料网格结构的重要结构参数,可对结构参数进行调整计算。选择图3中7 种典型网格结构进行参数调整计算[4]。

图2 无蒙皮复合材料网格结构参数Fig.2 Structural parameters of composite materials

图3 典型无蒙皮复合材料网格结构展开图Fig.3 Sketch maps of typical composites without skin
为缠绕成型方便,将纵筋环筋和螺旋筋的筋宽设置为等宽。壳体半径1 400 mm,壳体高度550 mm,筋条高度为9 mm,筋条宽度为4 mm。E1=120 GPa。计算结果见表1。
经过参数调整计算,可迅速找到工程上可行的参数组合,作为优化计算的输入,从而减小优化计算的工作量。

表1 典型网格结构参数计算结果Tab.1 Calculation results of typical grid structure
3.3 网格参数优化方法
经参数调整计算选取的网格参数不一定是最优的。模具上一旦加工出网格筋槽,再改变网格尺寸,会导致整个阳模的返修或报废。根据试验结果不断修正结构从而达到结构优化的办法,对于无蒙皮复合材料网格结构成本过高、周期过长,可应用有限元方法进行结构优化。其设计载荷、壳体的长度和半径以及筋条的材料常数均为已知量,可取筋条间距、筋条高度、筋条宽度为设计变量。其中筋条宽度是连续变量,筋条间距可由筋条数量决定,筋条高度可定义为单层厚度乘以某一整数。通过优化计算,最终得到结构质量轻、承载能力高的优化结构。可以通过提取单胞,利用单胞的复制、移动和旋转等操作来建立整个结构。
3.3.1 单胞建立
如图4所示,图中坐标值以单胞周向长度(L)、单胞轴向长度(H)和蒙皮端部长度(He)来表示,并有如下关系式:

式中,R1表示圆柱中面半径;Bn表示斜向筋条数;Ba表示筋条之间的夹角,此夹角取不同值时即可实现不同网格形式单胞的建立。He的意义是:圆筒总长度是一定的,沿轴向划分的单胞结构将不可能恰好整分圆筒轴向长度,于是圆筒蒙皮两端将会多出一段,将其定义为蒙皮端部长度。
按照图4中所示坐标创建节点node1、node2、node3和node 4,在需要加筋条的边上创建梁单元,用梁单元模拟筋条,在建模的同时自动完成网格划分工作。

图4 单胞示意图Fig.4 Schematic diagram of single-cell
3.3.2 结构成型
创建单胞后,通过对单胞进行一系列的变换得到整个结构的有限元模型。
首先将单胞进行轴向平移,然后运用与创建单胞类似的方法将两端的端部(即不够一个整单胞的部分)补全,再对网格进行细化,得到大单胞,如图5左图所示。此时的大单胞是一个平面图形。
利用场函数将平面图形映射到空间的圆柱面上,得到如图5右图所示的结果。

图5 大单胞及映射后的示意图Fig.5 Large signal-cell and mapping of diagram
将5 右图所示的结构绕x 轴复制一周得到所要建立的圆柱。若端框的高度不为零,则需要再添加端框,这个功能通过扫描来实现。最后去除模型中的重复节点和重复单元。到此复合材料网格结构有限元模型建立完毕,所建立的圆柱模型如图6所示。

图6 复合材料网格结构圆柱壳有限元模型Fig.6 Finite element model of composit material grid structure
由此可实现快速建模,结合遗传算法可对结构进行优化计算,从而得到最优结构参数组合。对于无蒙皮复合材料网格结构,仅对筋条进行建模及划分单元即可,其过程比有蒙皮复合材料网格结构简单。以表1中所列结果为初始输入,以上述方法快速建模对结构进行优化。优化结果为:筋条高度8.9 mm,筋条宽度4.2 mm,斜筋螺旋角22°,斜筋间距5.8°。
3.4 结构方案的确定及精确模型有限元计算
优化结果经圆整,与3.2 所述方案7 相同。根据工艺建议,降低筋条高度,加大筋条宽度。筋条高度接近优化尺寸,确定为8.5 mm。筋条宽度加大至12.75 mm。根据工程需要,结构上有一处240×250的开口,会降低结构的承载能力。对开口进行补强。补强后的承载效率可达原承载的90%以上。结构三维模型见图7。

图7 结构三维模型Fig.7 3D model of structure
建立精确的有限元计算模型,进行有限元计算。根据工程应用的实际情况,边界条件设置为半固支。结构应变图见图8。

图8 结构应变图Fig.8 Strain diagram of the structure
根据复合材料网格结构[2,4]试验情况,结构会在应变达到7 000 με 左右时失稳。考虑到无蒙皮复合材料网格结构各向筋条没有蒙皮支撑,其失稳应变定为6 000 με。经计算,不考虑开口边角处的应力集中,结构承载能力为1 510 kN,远大于轴压设计载荷333 kN。如图9所示。

图9 载荷-位移曲线Fig.9 Curve of load-displacement
4 无蒙皮复合材料网格结构的生产及试验
无蒙皮复合材料网格结构的成型装置可参照复合材料网格结构的成型装置[5]。由于结构无蒙皮,筋条缠绕时高度不易控制,太高则筋条高出阳模的部分成型质量及尺寸不好控制;太低则阴模无法压实筋条。可加深阳模筋槽,并制备与筋条同宽的硅橡胶条,在筋条完成缠绕后,将硅橡胶条置于阳模筋槽内,用于压实筋条。碳纤维选择性能稳定的国产碳纤维,其生产批量大、性能偏差小;同时大幅度降低生产成本。如图10~12所示。

图10 被替代的金属杆系结构Fig.10 The replaced metal rod structure

图11 试验件的安装及加载Fig.11 Installation and loading of test structure
试验表明,无蒙皮复合材料网格结构在满足设计要求的情况下质量为28 kg,较金属杆系结构减轻41%。结构的轴压承载能力为806 kN,虽然超过设计,但低于计算结果。试验过程中,测量得到的应变与有限元计算所得应变趋势相同,但结构没有在应变最大的开口处破坏(应变4 000 με),而是在网格节点产生破坏(应变3 600 με),这说明节点成型质量还有提高余地。根据工艺要求加大筋条宽度以减小筋条节点处的应力是低效率的加强方式,是受节点成型质量限制而采用的措施。只要提高节点质量,可将筋条高度加高到计算最优值、将筋条宽度减小一半而结构承载能力不会有明显下降。由此可进一步减重,同时试验破坏载荷将与计算值更为接近。

图12 破坏形式及位置Fig.12 The form and position of destruction
5 结论
采用无蒙皮复合材料网格结构可取得很好的减重效果。将设计生产出的无蒙皮复合材料网格结构应用于工程实践,满足了工程研制需要,同时实现了低成本、轻质化的目标,可广泛应用于级间段、卫星支架等结构。今后可将最优结构参数组合与自动化缠绕工艺、固化罐成型工艺等最优工艺方法结合起来,设计并生产出最优结构。

