Si3N4结合SiC耐火陶瓷高温抗疲劳断裂设计

袁 虎 杨自春 赵 爽 孙文彩

（海军工程大学舰船高温结构复合材料研究室，武汉 430033）

文 摘 为探究高温氧化条件下材料抗疲劳断裂的相关改进措施，在分析材料高温疲劳断裂过程的基础上，将有效场-子域模型和热-损伤断裂强度模型相结合，对高温氧化条件下Si3N4结合SiC 耐火陶瓷的微裂纹尺寸与强度和密度与强度的关系进行了模拟。结果表明：此类材料在高温氧化环境中微裂纹尺寸在（0 mm，0.5 mm］和密度至少为（0 m-2，104 m-2］的可行性范围内能抗疲劳断裂。这个结果对延长材料的使用寿命和确保设备运行的安全稳定性具有的指导意义。

0 引言

Si3N4结合SiC 耐火陶瓷在实际运行工况中往往受到高温氧化行为的影响。此类材料在外加负荷作用下的表面热应力为［1］：

式中，σ为材料的表面热应力，α为线胀系数，ΔT为热应力产生时的温差，E 为弹性模量，φ 为热应力衰减系数，其随着温度变化速率的降低而减小，在温度变化无限快的极端情况下趋近于1；ν为泊松比，其随温度的变化情况可忽略不计。

结合材料的断裂判据不难看出，一旦材料表面热应力产生的应力因子强度超出其断裂韧度，将使材料发生断裂失效行为。同时伴随着微裂纹的扩展与连通，并萌生出宏观裂纹。因此，寻求合适的密度和尺寸范围来制约微裂纹的扩展和连通，有利于提高此类材料的高温疲劳断裂强度，从而延长材料的使役寿命，提高设备运行的经济性与安全性［2-3］。

李卫国等［4-5］研究了综合温度对试件热物理性能和损伤在使用中的影响，提供了改进陶瓷材料高温抗疲劳断裂的热冲击模型，在数值模拟的基础上分析了热流率、冷却速率、热冲击起始温度和外部约束条件对超高温陶瓷材料抗热震性能的影响；CEMIAL［6］通过对比分析陶瓷材料晶粒尺度与各抗热冲击因子之间的关系，得出了当材料粗晶尺寸为22 μm时抗热冲击性能最好的结论；RASIM和CEMAIL［7］研究发现，Zr2O颗粒或者气孔会阻碍表面裂纹的扩展，从而改善材料的抗高温疲劳断裂性；李定玉［8］和王如转［9］则分别对升降温条件下陶瓷材料的热冲击损伤表征及其氧化行为进行了研究，从不同角度提出了改善陶瓷热防护材料高温抗疲劳断裂性能的措施。本文在上述研究的基础上，将结合耐火陶瓷自身的结构与其在设备中的运行工况，对材料高温断裂行为及其微裂纹在高温氧化条件下的演化过程进行研究。

1 高温疲劳断裂过程分析

1.1 升、降温过程中材料的热应力表征

通常情况下，将材料在热环境中所能承受的最大温差ΔTc作为其抗热冲击性能的表征。材料迅速冷却时，所受热拉应力可转变为第一个抗热冲击阻力参数来表征，此时的热应力衰减系数为1，该应力将导致裂纹失稳扩展，甚至断裂失效。而材料在一般冷却速率下的热拉应力常常结合热导率与第二个抗热冲击阻力参数来进行表征。对应的热冲击断裂临界温差为［8］：

材料在升温过程中，伴随着微裂纹的作用所产生的热压应力变化趋势缓慢，只结合第二个抗热冲击阻力参数来表征即可。对应的热冲击断裂临界温差为［8］：

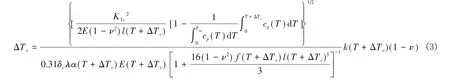
以上各式中，K1c为材料的断裂韧度，cp（T）为T温度下的定压比热容，ΔTc为导致材料断裂的临界温差，δc为陶瓷薄板的厚度，λ 为试件的表面热导率，E（T-ΔTc），α（T-ΔTc），k（T-ΔTc）分别为在T-ΔTc温度下材料的弹性模量、线胀系数和热导率，E（T+ΔTc），α（T+ΔTc），k（T+ΔTc）分别为在T+ΔTc温度下材料的弹性模量、线胀系数和热导率，l（T）=l0（T/T0）b和f（T）=f0（T/T0）a分别为微裂纹长度随温度的变化关系和单位内的微裂纹数目与温度的关系，它们可通过测取一定时间间隔下的微裂纹在不同初始温度T0和设定温度T的微裂纹长度和单位内的微裂纹数目来表征。

1.2 升、降温过程中材料的氧化行为表征

Si3N4结合SiC 耐火陶瓷在船舶锅炉的实际使用工况中，主要发生被动氧化机制。结合Pilling-Bedworth 定 义，SiO2在SiC 耗 尽 层 中 的 体 积 分数为［8-12］：

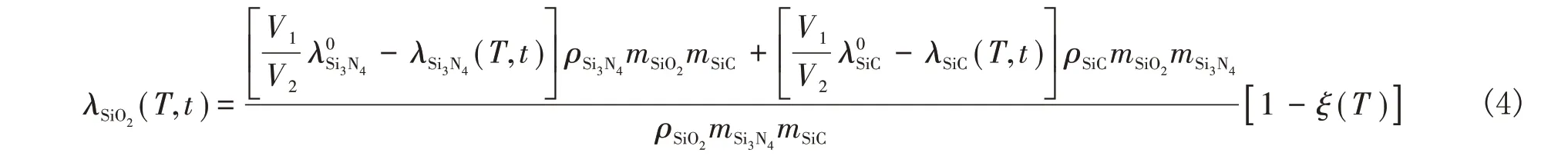
氧化生成孔隙的体积分数为：

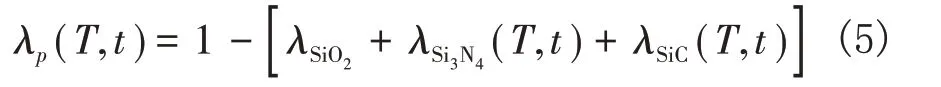
若孔隙在Si3N4基体中无限制的扩展，将最终导致微裂纹相互连通扩展，甚至生成孔洞造成试件断裂失效。结合等应变准则，SiC 耗尽层的弹性模量E如下［8］：

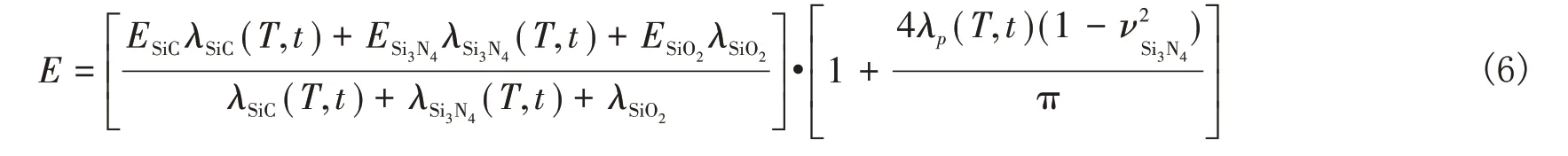
以上各式中，V1、V2分别为反应前后的固体体积，λ和λ0分别为物质反应过程中和t=0时的体积分数，ρ为物质的密度，m 为各相的指前因子和摩尔质量，ξ（T）为SiO2在不同温度下的迁移系数。

1.3 升、降温过程中材料的断裂强度表征

从上述热应力与氧化行为表征可看出，材料SiC耗尽层的强度作为材料自身强度的一个重要指标，其受微裂纹的尺寸和密度等参数的影响。结合图1所示的工程实际中的断口形貌，同时考虑热冲击下高温氧化行为对SiC 耗尽的影响，可将Si3N4结合SiC耐火陶瓷的高温疲劳断裂行为等价为材料在温度和氧化环境的共同作用下微裂纹的演化过程，如图2所。

图1 Si3N4结合SiC耐火陶瓷裂纹形貌Fig.1 Crack morphology of Si3N4 bonded SiC refractory ceramics

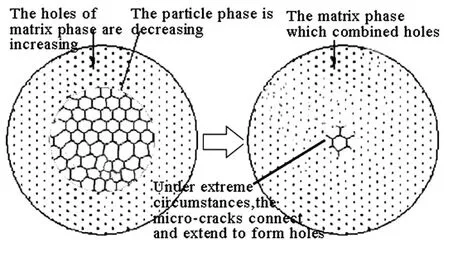
图2 耐火陶瓷疲劳断裂简化过程Fig.2 Simplified process of refractory ceramic fatigue

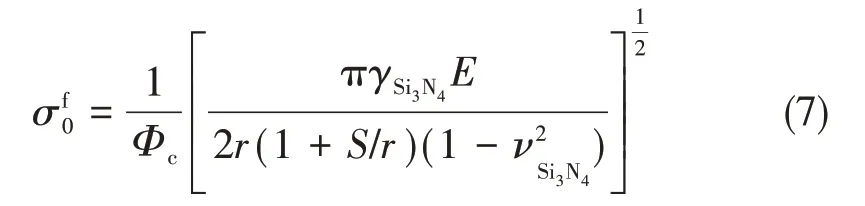
式中，γSi3N4为Si3N4的断裂表面能，r为SiC晶粒尺寸，S为缺陷尺寸，它们同时也共同决定着系数Φc的大小：

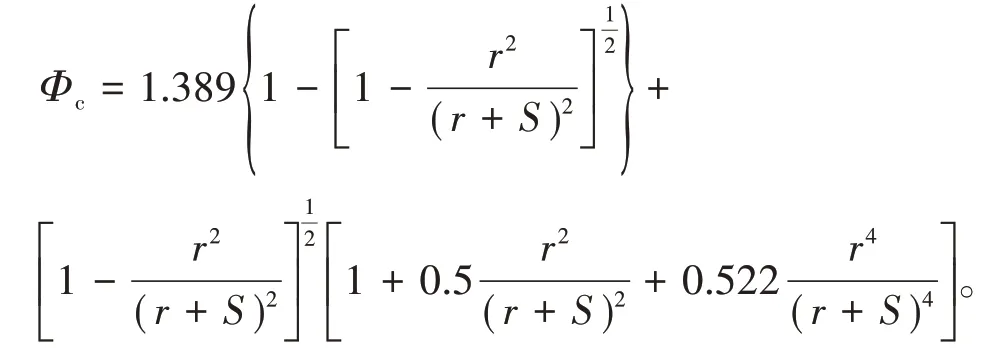
2 高温抗疲劳断裂设计

2.1 设计的适用范围

考虑高温环境下试件氧化行为和温度对微裂纹的共同作用，为提高对材料损伤行为表征的准确性，对设计的适用范围特作以下几点限定：（1）材料中的SiC 呈球形颗粒状均匀分布于Si3N4基质中；（2）各相同性的基体中微裂纹完全随机分布，所受外加载荷未受任何扰动；（3）材料在高温下能按氧化反应式充分完全反应，且循环载荷作用下晶粒的位错与滑移不可逆；（4）高温环境中，材料的泊松比和线胀系数受温度的影响不大，可忽略不计。

2.2 相关模型的建立

针对SiC 耗尽层的变化，选取有效场-子域模型模拟Si3N4结合SiC 耐火陶瓷微裂纹密度和尺寸在正常运行工况下的可行性范围。选取热-损伤断裂强度模型，模拟预防材料因过度高温氧化而生成孔隙的可行性条件。

2.2.1 有效场-子域模型

在远场均布载荷σ→∞的作用下，选取图3（a）中第a 条微裂纹周围半径R 为0.64 μm 的圆形区域作为子域Γ，区域外的微裂纹体作为有效场，可构建出有效场-子域模型。

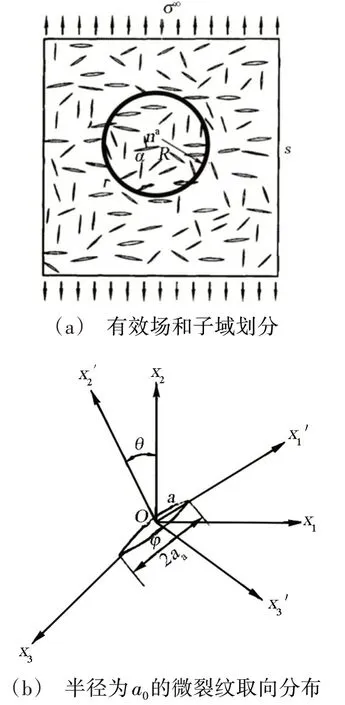
图3 有效场-子域模型图Fig.3 Figure of effective field-subdomain model

子域内微裂纹的相互作用可通过细观力学来直接求解，外部微裂纹体对该条微裂纹的影响则通过修正远场应力来实现。同时，建立整体坐标系（Ox1x2x3）和局部对应坐标系后，子域内半径为a0的微裂纹的取向分布如图3（b）所示。其中x2′轴与微裂纹的法线na相平行，x1轴与其的夹角与x2′轴和x2轴间的夹角θ 相等，x3与微裂纹长轴相平行，与x1′的夹角为φ［13］。根据微裂纹的相互作用和半径为a0的微裂纹的取向分布得到模型的相关表征式［13］。

2.2.1.1 有效场

在应力边界条件下：

在位移边界条件下：

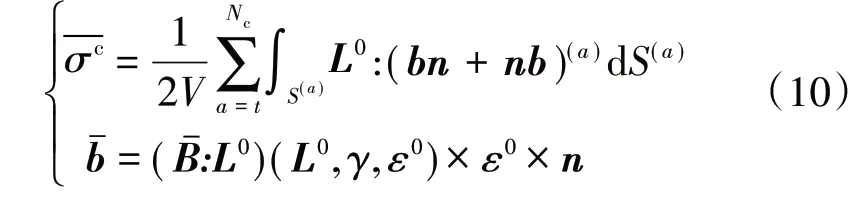
在远场应力作用下：

上述各式中，σ0为远场应力，s0为有效介质的柔度，ξ和η为修正系数，f为微裂纹密度因子，Nc为微裂纹总数，S（a）和P（a）分别为第a 个微裂纹的面积和前缘周长，和分别为总体平均应变和应力分别为基体的平均应变和应力和分别为微裂纹引起的平均应变的增加和平均应力的减少，L为材料刚度张量，V为代表体积单元，b（a）和n（a）分别为裂纹张开位移不连续矢量和法向单位矢量，-b 和-B 分别为张开位移和位移张量的平均，γ为裂纹的几何形状。

2.2.1.2 子域

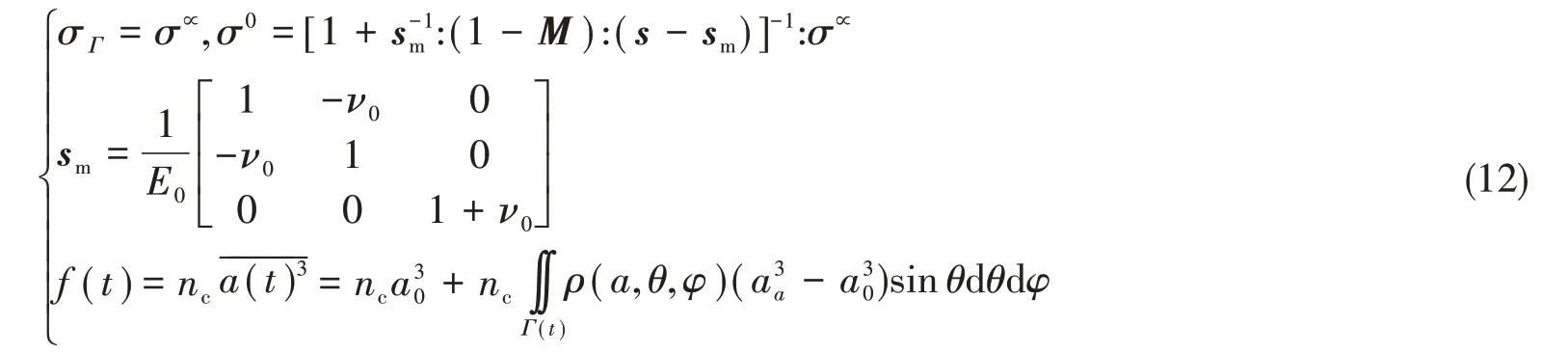
式中，σΓ为子域内的平均应力，sm和s分别为基体和夹杂Γ的弹性柔度张量，M为Eshelby张量，E0和ν0分别为基体弹性模量和泊松比，f（t）为子域内微裂纹密度，nc为每平米单位子域内的微裂纹数目，a（t）、a0和aa分别对应t时刻、扩展前和一次稳定扩展后的裂纹半径，ρ（a，θ，φ）为子域内微裂纹的取向概率密度函数：

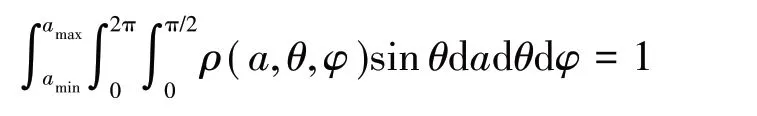
材料在受热损伤过程中，可视为取向均匀分布的二维平板，此时ρ（a，θ，φ）=1/2π，结合有效场和子域内的柔度和刚度对材料应力应变场的影响，在大量微裂纹作用下，其有效模量与微裂纹数目和尺寸的关系如下所示［13］：

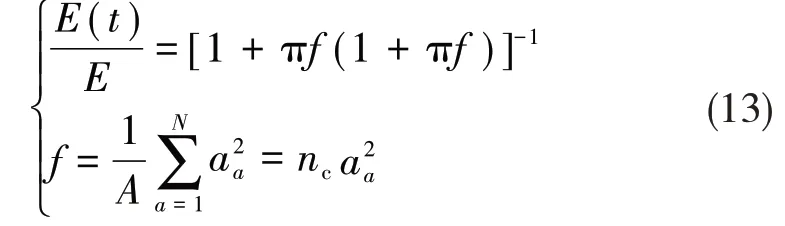
式中，E（t）为材料在t时刻的有效弹性模量，A 为子域Γ的面积，N为子域中的微裂纹总数，aa为第a条微裂纹的半长。

2.2.2 热-损伤断裂强度模型

结合式（7），Si3N4结合SiC 耐火陶瓷SiC 耗尽层热-损伤断裂强度模型的建立如下［9］：

式中，σt（hT，r，S，t）为计及氧化温度、微孔隙相变、裂纹尺寸和时间等机制影响下耗尽层断裂强度，σt（hT）为材料在初始损伤状态下与温度相关的断裂强度，为在参考温度下考虑损伤作用的断裂强度，σ0th为在统一参照温度和初始状态下的断裂强度，由此，σf0/为常温下的损伤项对材料断裂强度的部分作用，cp（T）为在压力p 和温度T 下Si3N4的比热容，ESi3N4(T)和ESi3N4分别为Si3N4在T温度下和在初始温度下的弹性模量，νSi3N4为Si3N4的泊松比，ΔHM和Tm分别为Si3N4的熔化热和熔点。

将式（13）代入式（14），材料SiC 耗尽层的断裂强度与微裂纹各参数的关系即为：

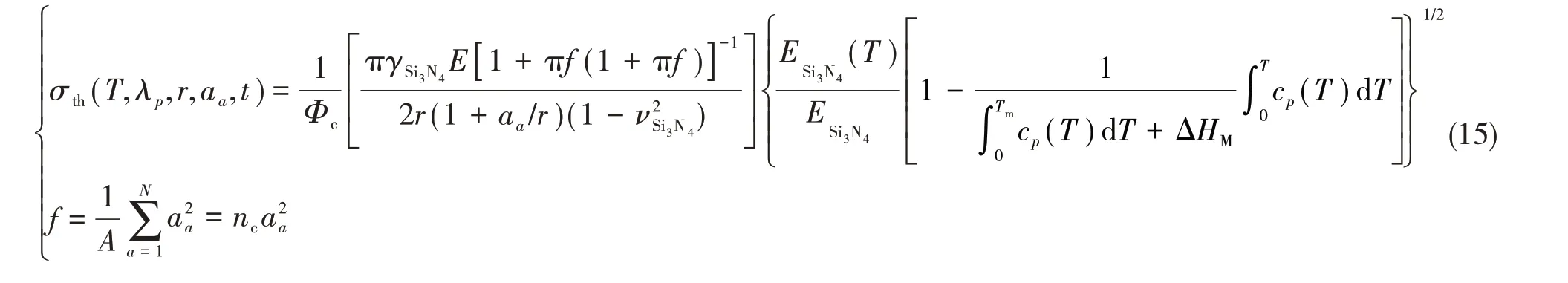
2.3 设计过程探究

Si3N4结合SiC 耐火陶瓷相关物性参数如表1所示［14-15］。通过文献［16］可知，Si3N4结合SiC耐火陶瓷在1 546 ℃下的受拉损伤最严重。

表1 Si3N4结合SiC耐火陶瓷物性参数Tab.1 Physical parameters of Si3N4-SiC refractory ceramic

为满足工程实际，假设SiC 颗粒尺寸为0.5 mm的材料在氧气充足、温度为1 546 ℃的条件下以形核方式演化。此时，可计算得cp（T）≈363.15 J/mol，ΔHM≈129.27 kJ/mol，式（15）即可简化为材料SiC 耗尽层的断裂强度与微裂纹尺寸和密度的关系式：

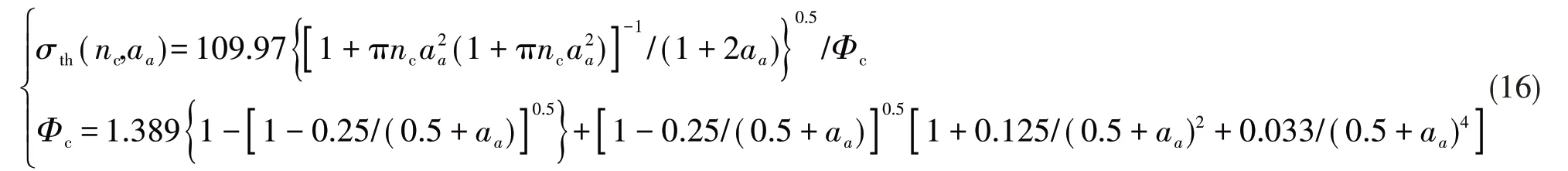
在给定每平米单位子域内的不同微裂纹数目nc时，材料SiC 耗尽层的断裂强度与微裂纹尺寸的关系如图4所示。

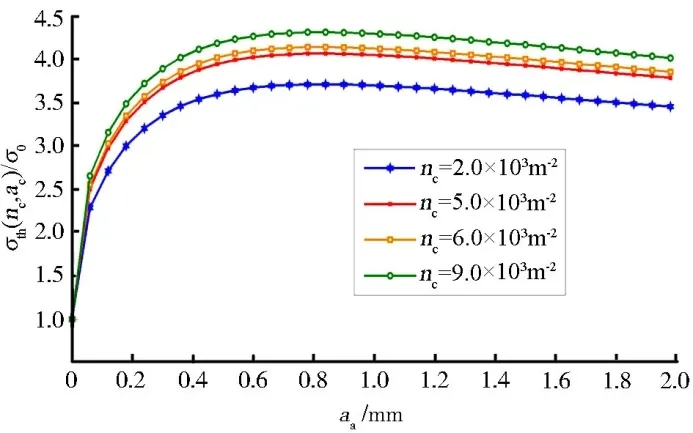
图4 强度与微裂纹尺寸的关系Fig.4 Relationship between strength and micro-crack size

从图4中可看出，在子域内微裂纹数目相同的情况下，材料SiC 耗尽层强度随微裂纹尺寸的增加先迅速增加，后缓慢增加，最后呈下降趋势，可看出，尺寸在（0 mm，0.5 mm］内，增韧效果最佳。在相同尺寸下，SiC 耗尽层强度随子域内微裂纹数目的增加，其增加趋势逐渐变缓。

为进一步探究不同微裂纹尺寸下，材料SiC 耗尽层强度随子域内微裂纹数目的变化关系，模拟了当微裂纹尺寸为0.1、0.2、0.5 和0.8 mm 时的情况，如图5所示。从图5可看出，随着单位子域内微裂纹数目的增加，SiC 耗尽层的强度先增加后平缓。当微裂纹尺寸＜0.5 mm 时，子域内相同数目的微裂纹的耗尽层强度也在相同尺寸幅值上的增加大于当微裂纹尺寸＞0.5 mm 时，这也间接证明了前述分析的准确性。同时可看出，每平米单位子域内微裂纹的条数在（0 m-2，104m-2］内，也能达到很好的增韧效果。

SiC 耗尽层强度的增加也在一定程度上增加了材料的强度［9］。因此，综合上述分析可得出，当材料引入的微裂纹条件在允许范围内时，均能达到高温抗疲劳断裂的目的。由此，针对材料抗高温疲劳断裂的方案，可作如下设计：在氧气充分，氧化温度满足T≤1 650 ℃的条件下，适当引入上述条件限制下的微裂纹。若超出这一范围，材料的SiC 氧化保护层将不再稳定，产生大量孔隙导致微裂纹连通，甚至生成孔洞致使材料的强度下降。

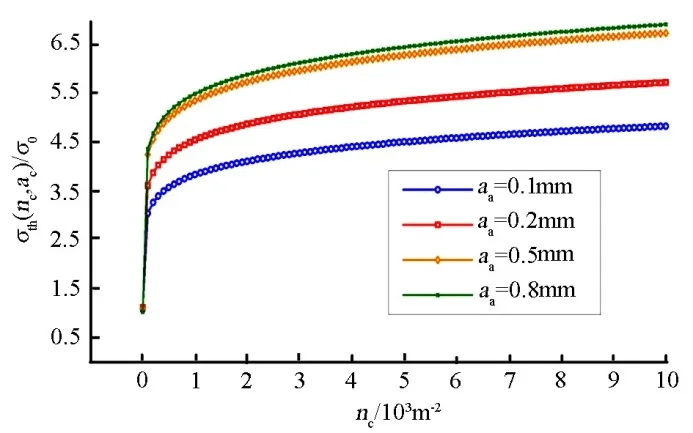
图5 强度与微裂纹密度的关系Fig.5 Relationship between strength and micro-crack density

3 设计的评估

材料在高温氧化条件下的受热冲击环境中，一定参数范围的微裂纹，可显著提高材料的断裂强度。联系工程实际，将材料的有效弹性模量代入式（1），可通过表面热应力与微裂纹的关系对上述设计方案的可行性进行评估。代入后的表达式为：材料在1 545 ℃的高温氧化受热冲击环境中，ν约为0.18，α约为4.5×10-6/K，假设温差ΔT为40 ℃，根据前文降温过程中的热应力表征情况，此时的热应力衰减系数φ=1。

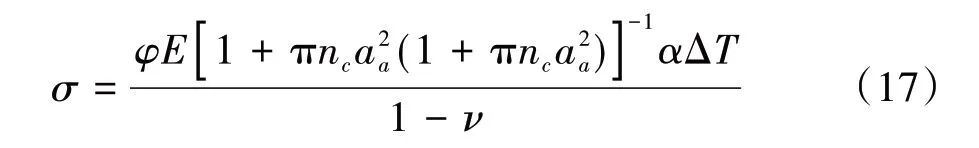
当单位子域内微裂纹数目分别为2.0×103、5.0×103和8.0×103m-2时，选取微裂纹尺寸对材料强度作用较小的区间范围［0.5 mm，1 mm］对上述方案进行验证，区间内所受热应力随微裂纹尺寸的变化关系如图6所示。从图6可看出，在该尺寸区间内，材料所受热应力随微裂纹尺寸的增加，下降幅度逐渐变缓，最后趋于平缓。这说明微裂纹对热应力的影响是随其尺寸的增加而减弱的。同时在子域内微裂纹数目增值相同的情况下，在同一微裂纹尺寸下材料所受热应力的下降幅度也明显变小，这说明微裂纹密度对热应力的影响也是逐渐变缓的。

图6 热应力与微裂纹尺寸的关系Fig.6 Relationship between thermal stress and micro-crack size

为进一步验证上述材料所受热应力与微裂纹密度之间的规律，选取微裂纹尺寸为0.2、0.5 和0.8 mm 的情况，在单位子域内微裂纹数目为［0.9×103m-2，104m-2］内对热应力随子域内微裂纹数目的变化关系进行如图7所示的模拟。从图7中可看出与图6相同的变化规律。即在该区间范围内，材料所受热应力随区域内微裂纹数目的增加，下降幅度逐渐变缓，最后趋于平缓。同时在微裂纹尺寸增值相同的情况下，在单位子域内同一微裂纹数目下材料所受热应力的下降幅度也明显变小。

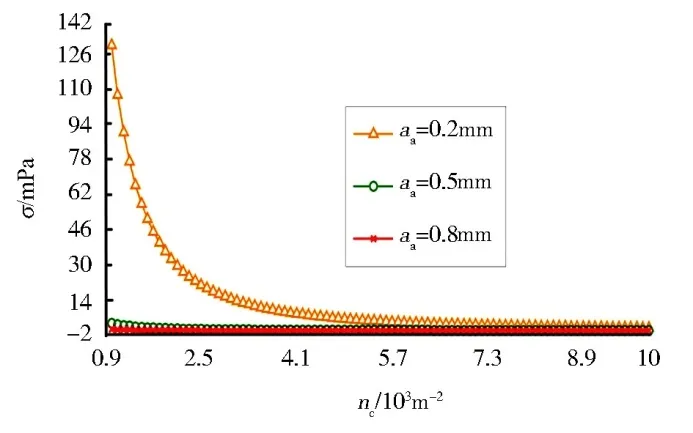
图7 热应力与微裂纹密度的关系Fig.7 Relationship between strength and micro-crack density

综合上述热应力与微裂纹尺寸和密度的对应关系，进一步验证了高温抗疲劳设计方案的合理性。即通过预制合理尺寸和密度范围内的微裂纹，可在一定范围内增强材料的强度。

4 结论

Si3N4结合SiC 耐火陶瓷在受热冲击的过程中，往往伴随着系列的氧化行为。在对材料高温疲劳行为进行分析的基础上，对实际工况下微裂纹的相关性能进行了分析和验证。发现在给定温度条件下，微裂纹尺寸和密度控制在合理范围内，材料强度均能有所提高。据此，得出如下结论：

（1）当微裂纹尺寸在（0 mm，0.5 mm］内，单位子域内微裂纹条数控制在至少为（0 m-2，104m-2］内时，材料将通过形核方式释放部分残余应力，对所受的外部载荷起到有利的屏蔽作用，同时也削弱了材料中储存的弹性应变能，减少了材料的受热损伤；

（2）一旦微裂纹的尺寸和密度超出上述可行性范围时，大量的微裂纹将会扩展连通，甚至形成孔洞，在材料内侧裂纹尖端起着对外加应力的放大作用。