基于二次回归正交试验的汽轮机排汽缸加装导流板的研究

曹丽华，周凯，司和勇



基于二次回归正交试验的汽轮机排汽缸加装导流板的研究

曹丽华1，周凯2，司和勇1

（1．东北电力大学能源与动力工程学院，吉林省 吉林市 132012；2．哈尔滨汽轮机厂有限责任公司，黑龙江省 哈尔滨市 150040）

以某600MW汽轮机为研究对象，应用计算流体力学软件CFX对低压缸末级和排汽缸的耦合模型进行了数值模拟，基于二次回归正交试验，在排汽缸上端安装导流板来削弱通道涡对排汽缸气动性能的影响，得到了导流板安装参数与静压恢复系数之间的回归方程。方程呈现非线性关系，显著不失拟，且三因素之间互不影响。求解回归方程的最优解，得出最佳的导流板安装方案。安装导流板后，通道涡被破碎，排汽缸的气动性能得到了明显的改善。排汽缸出口的静压恢复系数提高3.008%，总压损失系数降低5.789%，出口截面标准偏差降低了3.043。并且，不同负荷下优化后排汽缸出口的静压恢复系数均大于优化前。

汽轮机；排汽缸；导流板；二次回归正交试验；气动性能

0 引言

排汽缸是连接汽轮机低压缸末级和凝汽器的重要部件，其内结构复杂，主要由扩压器、蜗壳、辅助结构构成，排汽缸内部的蒸汽呈复杂的三维流动。由于蜗壳上端空间较为狭小，排汽在蜗壳上端形成了一个较大的漩涡(即通道涡)，而后分别从两侧向下分流，形成2个略小的通道涡，扩压器两侧的汽流经过翻转后汇入通道涡使其不断壮大，一直延伸到排汽缸出口，严重影响了排汽缸的气动性能[1]。因此，从破坏通道涡的结构入手，在排汽缸内加装导流板，成为改善排汽缸气动性能一种有效手段。

目前，已经有很多对排汽缸进行改造的文献。刘晖明[2]通过对300 MW汽轮机排汽通道进行模型吹风实验，对加装导流板前后流场对比并通过数值模拟分析，发现加装导流板能够改善流场的不均匀性，减小凝汽器的汽阻，进一步减小凝汽器的传热端差，提高凝汽器的经济性和安全性。文献[3-5]的研究发现：在排汽通道内加装导流装置可以提高排汽缸静压恢复系数和改善出口流场的均匀性。文献[6-8]对导流环型线进行优化设计，说明了优化后的导流环可以改善扩压管内的流动状态及低压排汽缸内气动性能。

虽然单纯的依靠数值计算可以进行导流环的优化设计，但周期太长。回归正交试验结合了回归分析和正交试验的优势，通过合理设计试验方案，减少试验次数，选择适当的试验点，对试验指标和因素之间的数据整理、回归方程的建立以及回归方程显著性检验的统一考虑，解决试验因素筛选及试验优化问题[9]。而二次回归正交组合设计是在一次回归正交试验设计的基础上再增加一些特定的试验点，通过适当的组合形成试验方案，提高整个回归空间内的拟合度。鉴于利用正交试验对结构参数进行优化已在导流环、汽封和机床上得到应用[10-12]。因此，本文以某600MW汽轮机为研究对象，耦合末级叶片和排汽缸，采用三因素二次回归正交试验设计方法安排数值模拟，目的是寻求排汽缸静压恢复能力最佳时的导流板的参数。建立回归方程，旨在研究静压恢复系数与导流板参数之间的关系。通过显著不失拟的回归方程及约束条件求解出最优值，最终得到优化设计的导流板参数，并分析安装导流板前后的排汽缸气动性能的变化。

1 二次回归正交实验

1.1 正交实验设计

导流板参数设计：分别选取两板的间距1、导流板的高度2以及导流板的长度3作为回归正交实验的三因素，如图1所示。取值范围结合某600MW汽轮机组：1=300~500mm、2=530~ 870mm、3=400~1200mm。

本文采用三因素二次回归正交试验设计方法安排数值计算，得出回归方程，根据函数最优化问题，得出指标静压恢复系数最大时的导流板参数，同时各因素水平z(=1, 2, 3)变化时静压恢复系数的变化趋势也显而易见。设定因素水平编码如表1所示。

图1 导流板安装参数示意图

表1 三因素水平编码表

1.2 试验实施方案

根据正交表，设计14个常规方案进行数值模拟；设计3个零水平正交试验方案，用以对回归方程的失拟性进行检验，共计17个试验方案。得到与z(=1,2,3)之间非线性关系的三元二次回归方程：

将式(1)转化为求解非线性一般约束最优化问题，如方程组(2)所示，优化问题的最优解就是安装导流板的最佳方案。

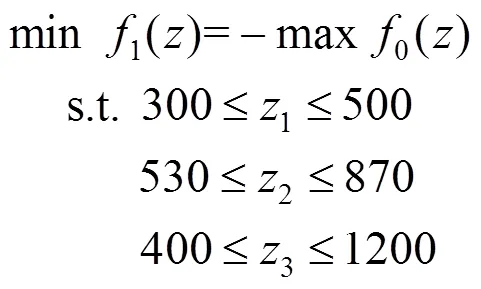
根据式(2)求得最优解，得到最佳的导流板安装方案为：两板间距1为429mm、导流板高度2为700mm、导流板宽度3为969mm。

1.3 数值模型

采用结构化网格和非结构化网格相结合的方法，排汽缸应用ICEM划分网格，为非结构网格，末级采用Turbo-Grid划分网格，为结构网格。为了能够更加真实的地反映末级叶片出口与排汽缸进口之间交界面流动参数的传递，对排汽缸进口环形面的网格进行加密；同时考虑到边界层流动对整个流场的影响，末级流域和排汽缸的近壁面处进行网格加密，如图2所示。

图2 安装导流板的排汽缸网格

利用CFD数值计算软件CFX14.0平台，基于压力和速度耦合关系的SIM2PLEC算法，结合均匀介质多相模型和水蒸气平衡相变模型，采用有限元的有限体积法求解三维可压缩稳态雷诺时均N-S方程，选用-湍流模型，近壁面流动区域采用salable壁面函数法，对流项采用高阶迎风精度格式，数值残差收敛标准为RMS低于10-4。工质选用IAPWS-IF97工质库中“steam3vl”平衡态湿蒸汽模型，参数为汽轮机热耗率验收工况(THA)下运行数据。末级动、静叶叶栅之间的交界面与动叶叶栅、排汽缸之间的交接面处理均采用“Frozen Rotor”模型。进口边界条件采用“Mass-flow-inlet”边界，100%THA工况时质量流率为74.736kg×s-1，排汽缸出口延伸段压力为给定值，平均静压为6000Pa。

1.4 评价指标

为了更好的描述排汽缸的性能，引入3个特性参数，静压恢复系数pr、总压损失系数tpl和标准偏差V。

静压恢复系数：

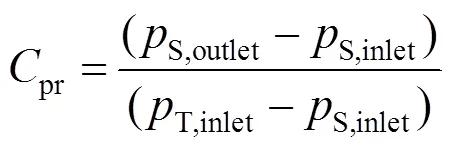
总压损失系数：

标准偏差：

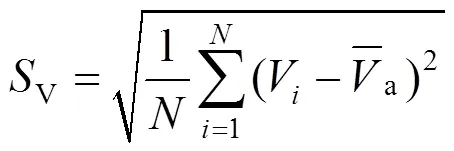
由式(3)—(5)可知，pr越大，扩压器的导流扩压作用对排汽缸回收动能的能力越强；tpl越小，汽流在扩压器中由动能转化为压力能而引起的压损越小，排汽缸性能越好；V越小，排汽缸出口的速度场分布越均匀。

2 安装导流板后排汽缸的气动性能综合评价

2.1 安装导流板后排汽缸流场分析

图3为优化前和优化后的排汽缸内三维流线图。可以直观看出，安装导流板后，末级排汽向上翻转后被导流板挡住向两边分开，原本在排汽缸上端的大通道涡被缩小，两端的小通道涡也随之缩小，速度逐渐趋于均匀。

图3 优化前后排汽缸内三维流线图

图4为优化前和优化后的排汽缸子午面的流线分布图。优化前，排汽缸顶部的通道涡向两侧分离成2个涡向下延伸，从图中子午面流线可以看出，优化前排汽缸两端为2个较大的通道涡，优化后其中一边被分离成2个较小的涡，而且导流环根部内弧区的涡也消失了。这说明其中一端的通道涡被破碎了，导流板起到了有效作用。

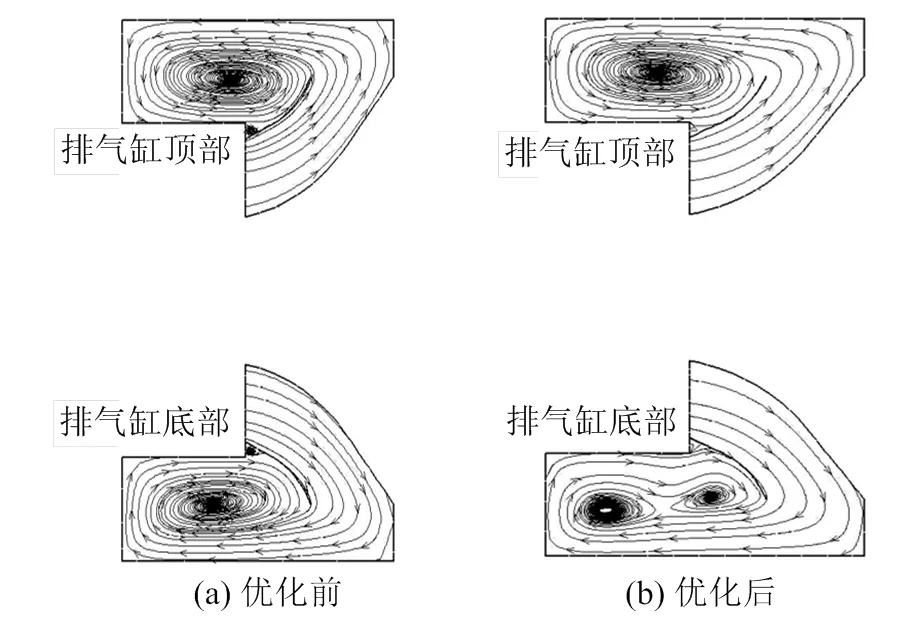
图4 优化前后排汽缸子午面流线图

图5为优化前和优化后排汽缸出口的速度分布云图。从图5可知，优化前排汽缸两端通道涡延伸到排汽缸底部，形成了2个低速区，优化后其中一端的通道涡已被破碎，极低速区消失，另一端的低速区也明显缩小，而中间的高速区也减少，出口截面速度分布的均匀性明显提高。

2.2 安装导流板后排汽缸性能分析

优化前后各指标如表2所示。由表2可知，优化后排汽缸总压损失系数降低了5.789%，静压恢复系数提高了3.008%，出口截面标准偏差降低了3.043，这表明安装导流板后排汽缸的能量损失减小，出口流场的均匀性得到了改善

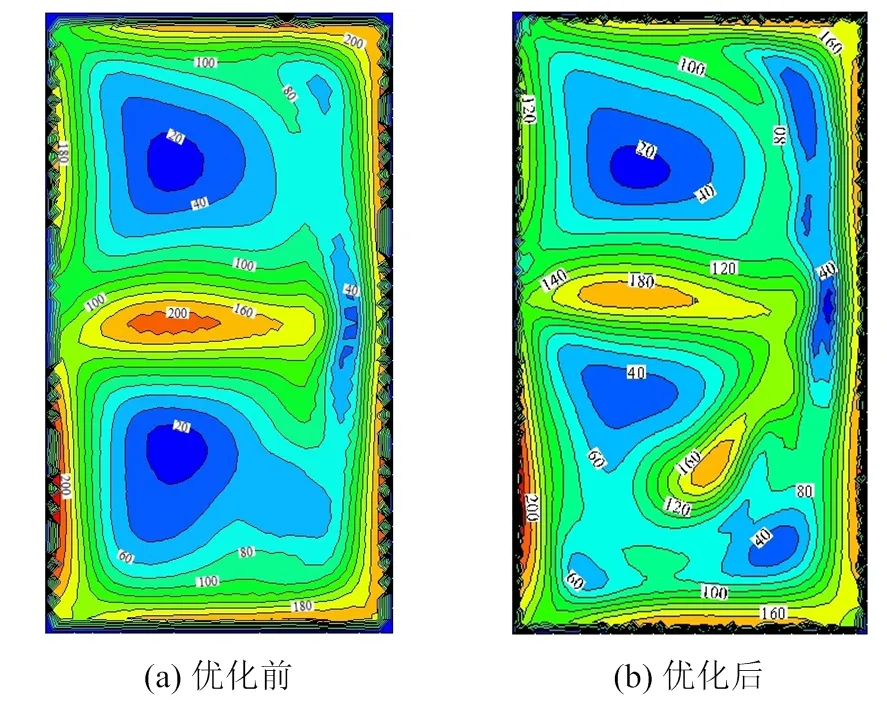
图5 优化前后排汽缸出口速度流场分布(m/s)

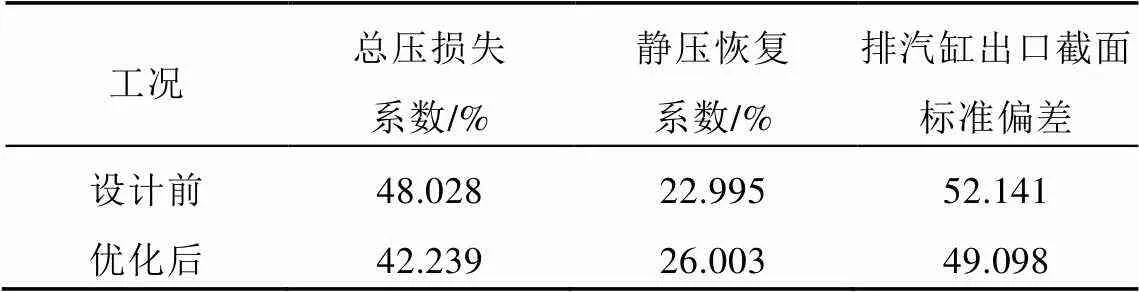
表2 导流板设计前后的性能评价指标对比一览表

图6为不同THA工况下优化前后排汽缸气动性能指标。可以看出，优化前，随着负荷的降低，排汽缸出口的静压恢复系数逐渐降低，50%THA工况时达到了负值；而优化后不同负荷下排汽缸出口的静压恢复系数均大于优化前；优化后不同负荷的总压降均小于优化前，即优化后总压损失降低。这表明安装导流板的优化设计在低负荷下也是可行的。

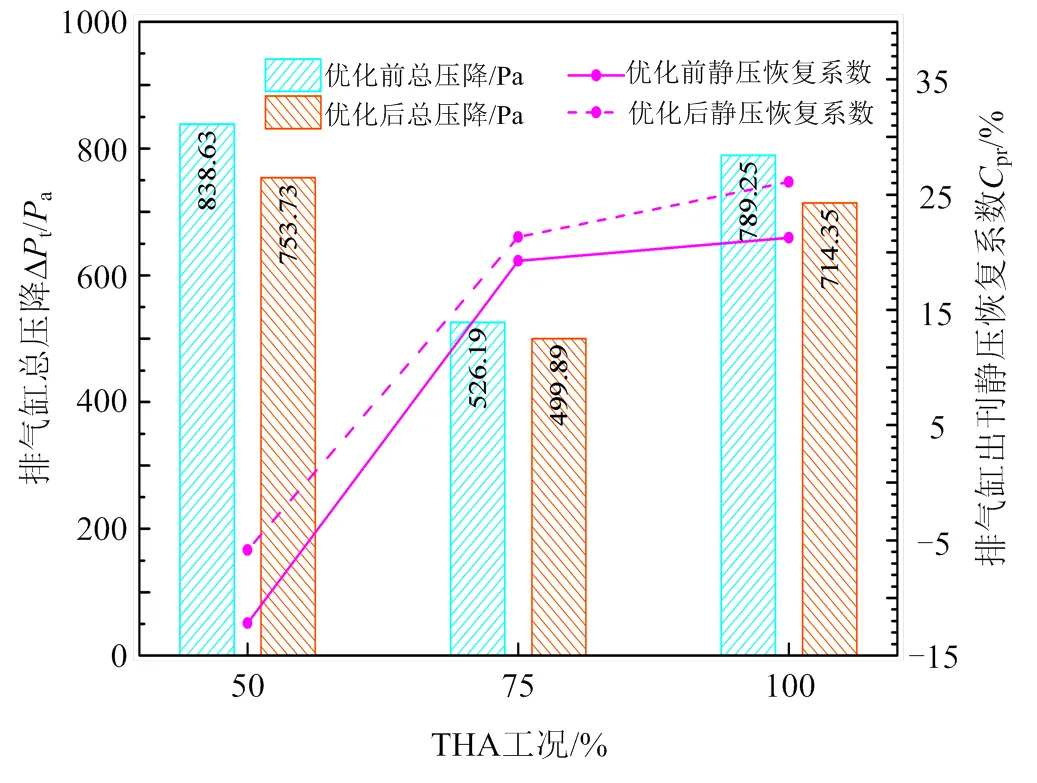
图6 不同THA工况下排汽缸气动性能指标

3 结论

采用三因素二次回归正交试验对某 600MW汽轮机低压排汽缸进行了优化设计，并分析优化前后排汽缸内气动性能的变化情况。得出以下结论：

1）在排汽缸上端安装导流板，通道涡被破碎，削弱了通道涡对排汽缸气动性能的影响，这种改善排汽缸气动性能的方法是可行的。

2）基于二次回归正交试验，可得到导流板安装参数与静压恢复系数之间的回归方程。求解回归方程的最优解，可得到最佳的导流板安装方案。

3）安装导流板后，排汽缸出口的静压恢复系数提高了3.008%，总压损失系数降低了5.789%，出口截面标准偏差降低了3.043。并且安装导流板的优化设计在低负荷下也可以改善排汽缸的气动性能。

[1] 徐旭，康顺，蒋洪德．低压蒸汽透平排汽缸内能量损失的数值研究[J]．北京航空航天大学学报，2002，28(6)：52-55．

[2] 刘晖明．300MW机组汽轮机排汽通道安装导流装置设计研究[J]．电力科学与工程，2012，28(3)：75-78．

[3] 谢伟亮，王红涛，竺晓程，等．汽轮机低压排汽缸内导流挡板对其性能影响的分析[J]．动力工程学报，2011，31(5)：347-351．

[4] 魏春枝，杨新健，陈顺宝．排汽缸内置挡板对扩压管出口下游漩涡的影响[J]．汽轮机技术，2014，56(3)：203-205．

[5] 付文锋，杨新建，周兰欣，等．某600MW汽轮机低压末级排汽通道耦合流动三维数值模拟及其结构优化[J]．中国电机工程学报，2014，34(14)：2267-2273．

[6] 陈川，付经伦，刘建军．汽轮机排汽通道优化设计与性能分析[J]．工程热物理学报，2009，30(8)：1295-1298．

[7] Yoon S，Stanislaus F，Mokulys T，et al．A three-dimensional diffuser design for the retrofit of a low pressure turbine using in-house exhaust design system[C]// ASME of Turbomachinery．Vancouver，Canada，2011．

[8] Musch C，Stuer H，Hermle G．Optimization strategy for a coupled design of the last stage and the successive diffuser in a low pressure steam turbine[C]//ASME of Turbomachinery，Vancouver，Canada，2013．

[9] 任露泉．试验优化设计[M]．北京：机械工业出版社，1987：1-4．

[10] 曹丽华，林阿强，张岩，等．基于二次回归正交试验的排汽缸导流环优化设计[J]．机械工程学报，2016，52(14)：157-164．

[11] 张勃，吉洪湖，杜发青，等．基于正交法的直通篦齿封严齿形几何参数对换热特性影响的试验研究[J]．机械工程学报，2013，49(4)：134-139．

[12] 邓聪颖，殷国富，方辉，等．基于正交试验的机床结合部动刚度优化配置[J]．机械工程学报，2015，51(19)：146-153．

Study on Installing Deflector in Exhaust Hood of Steam Turbine Based on Quadratic Regressive Orthogonal Experiment

CAO Lihua1, ZHOU Kai2, SI Heyong1

(1. School of Energy and Power Engineering, Northeast Electric Power University, Jilin 132012, Jilin Province, China; 2. Harbin Turbine Company Limited, Harbin 150040, Heilongjiang Province, China)

A combined numerical simulation is conducted to couple fluid flow between exhaust hood and last-stage blades of a 600MW steam turbine using the computational fluid dynamics software CFX. Based on quadratic orthogonal regression design, the flow guide device at the top of the exhaust hood is installed. The regression orthogonal equation between the installation parameters of the guide plate and the coefficient of static pressure recovery is obtained. The equation is remarkably unlost with nonlinear relation and there is no influence among the three factors. The optimal solution of the regression equation is solved. The channel vortex is broken Project Supported by the National Key R&D Plan (2017YFB0 902100). and the aerodynamic performance of the exhaust hood is improved obviously after the diversion plate is installed. The static pressure recovery coefficient of exhaust hood outlet is increased by 3.008%, the total pressure loss coefficient is reduced by 5.789% and the standard deviation of the outlet is reduced by 3.043. The static pressure recovery coefficient of exhaust hood outlet under different loads after the optimization is always higher than that before the optimization.

steam turbine; exhaust hood; flow guide device; quadratic regressive orthogonal experiment; aerodynamic performance

10.12096/j.2096-4528.pgt.18222

2018-11-05。

曹丽华(1973)，女，博士，教授，研究方向为汽轮机经济性分析与优化运行，clh320@126.com。

曹丽华

国家重点研发计划项目(2017YFB0902100)。

Project Supported by the National Key R&D Plan (2017YFB0 902100).

(责任编辑 车德竞)