电动汽车参与风电场输出功率波动平抑方法研究

陈宇，彭潇，丁婧，王亚洲，邵敬平



电动汽车参与风电场输出功率波动平抑方法研究

陈宇1，彭潇2，丁婧3，王亚洲1，邵敬平1

（1．湖北华电西塞山发电有限公司，湖北省 黄石市 435001； 2．国网湖北省电力有限公司荆州市荆州区供电公司，湖北省 荆州市 434100； 3．国网湖北省电力有限公司鄂州市鄂城区供电公司，湖北省 鄂州市 436000）

由于风电固有的随机性与间歇性，使得风电场输出功率往往具有较大的波动。然而考虑到储能装置的昂贵成本，单独为风电场配置储能装置不利于其经济运行。为此，文中针对考虑电动汽车参与的风电场输出功率波动平抑方法进行了研究。根据国家标准中风电“有功功率变化”的要求，通过爬坡率概念来描述风电场输出功率变化率。采用鲁棒优化的方法处理风电出力的不确定性，建立风电机组和电动汽车协调控制的双层优化模型：上层模型决策者是风电场，以风电场售电收益最大化为目标函数；下层模型决策者是电动汽车车主，以电动汽车电费支出成本最小化为目标函数。通过线性规划对偶定理和Karush-KuhnTucker(KKT)最优性条件将此鲁棒优化模型转化为混合整数线性规划问题进行求解。最后，通过仿真结果验证了所提模型和方法的有效性。

风电场；电动汽车；功率波动；鲁棒优化；双层优化

0 引言

随着全球环境问题日益严重，世界各国对清洁能源、可再生能源发电的关注度日益提高。在各种可再生能源领域中，风能作为清洁能源储量极为丰富[1-2]。然而，风能随天气条件的变化很大，具有随机性与间歇性，由于这种不确定性和波动性，使得风电场的输出功率往往具有很大的波动，严重影响电网的安全性与稳定性[3-4]。因此，平滑风电输出功率曲线是风电发展道路上一个必须解决的问题。

电池储能系统(battery energy storage system，BESS)具有快速响应特性，能有效平抑风电场输出功率的波动，是缓解电力系统调频压力的有效措施。储能在可再生能源并网中扮演了一个很重要的角色，如提高电能质量、限制电压波动、减少系统运行成本[5-6]。文献[7]提出一种储能容量最优配置的方法，该方法以平滑时间常数-合成输出标准变差特性作为风电功率波动平抑效果的评价指标，进而通过成本性能比计算出风电场的最优储能配置。文献[8]基于双层电容器和铅酸电池储能的等效电路进行数学建模，解决分布式可再生能源中风电引起的功率波动问题。文献[9]提出一种储能最优运行策略方法，该方法基于频谱分析确定混合储能系统(hybrid energy storage system，HESS)容量的方法，充分利用了超级电容和蓄电池的优势互补，建立以利润最大为目标的机会约束规划储能运行策略，结合蒙特卡罗算法进行求解，确定储能的最优运行。文献[10-11]提出蓄电池充放电控制策略，从而提高储能设备的使用寿命，同时解决分布式可再生能源中风电引起的功率波动问题。文献[12-13]通过构建钒电池的数学模型，分析钒电池的能量状态与端电压的变化特征，提出了相应的充放电策略，仿真结果表明改策略能有效地改善风电功率波动问题。文献[14]提出量化风电功率输出要求的风电功率波动特性指标，构建立了电池和超级电容相结合的复合储能系统双层优化配置模型。

在风电功率输出要求和复合储能成本的约束条件下进行求解，所得优化配置结果使储能系统投资成本最小。考虑到储能价格昂贵，储能装置的接入会影响系统运行的经济性，可利用风电场内部已有的储能装置参与风电场输出系统功率调节。

随着V2G(Vehicle-to-grid)技术的不断发展[15-16]，电动汽车在实现其行驶功能的基础上，可通过控制其充放电功率，平抑风电场输出功率波动，达到单独配备储能装置的效果。

1 风电场输出功率波动问题描述

在电力系统中，频率是表征电能质量的重要指标之一，保证频率符合要求是电力系统运行调度的一项重要任务。风电出力具有较强的随机性、波动性和反调峰性等特征。随着风电渗透率不断增加，风电出力变化率已成为影响电力系统频率稳定的关键因素，因此，风电并网发电功率变化应当满足电力系统安全稳定运行要求。根据《GB/T 19963—2011风电接入电力系统技术规定》对风电并网运行时输出功率变化量的规定，建立风电场输出功率变化率表达式[17]，如式(1)所示：

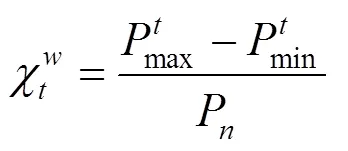
2 基于鲁棒优化的风电机组与电动汽车联合调度模型

2.1 风电出力不确定性集合

鲁棒优化模型中常用盒式不确定集形式描述不确定性变量的波动范围，但盒式决策空间过于保守，所以本文选择解的保守度可控制的多面体不确定集合代替盒式不确定集合。为了计算方便，通常要求不确定性集合为闭凸集，一种常用的多面体不确定性集合构造方法[18]，如式(2)所示：

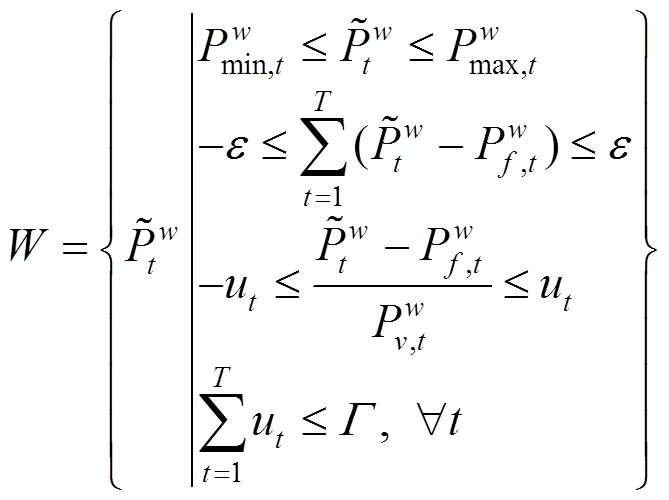
2.2 鲁棒优化调度模型

以含电动汽车的风电场为研究对象，充分利用电动汽车的充放电功能应对风电输出功率波动。以风电场售电利润最大化和内部电动汽车用户电费支出最小化为目标函数，建立了风电机组和电动汽车协调控制的双层优化模型，上层模型决策者是风电场，下层模型决策者是电动汽车车主。双层优化结构如图1所示。

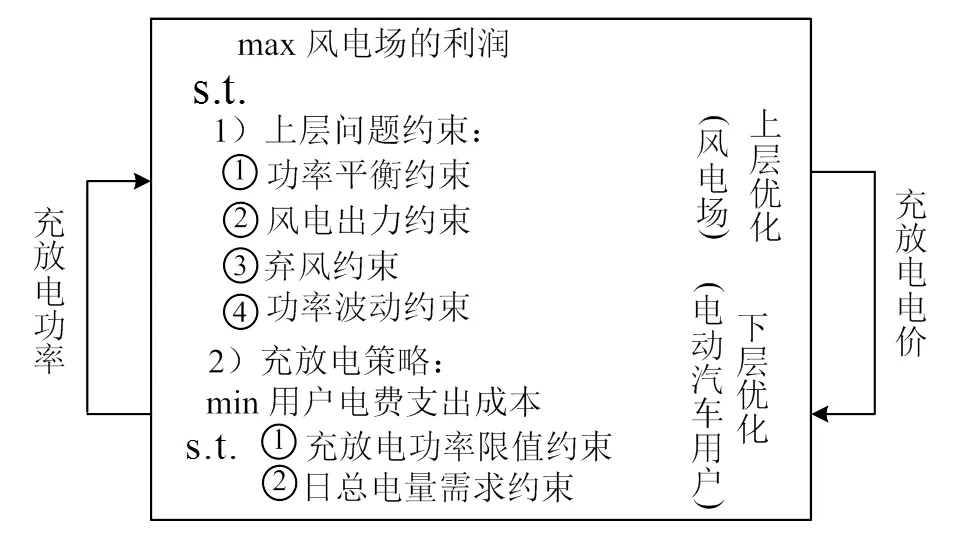
图1 双层优化结构示意图

1）上层优化模型。

风电场的输出功率优化问题如下：

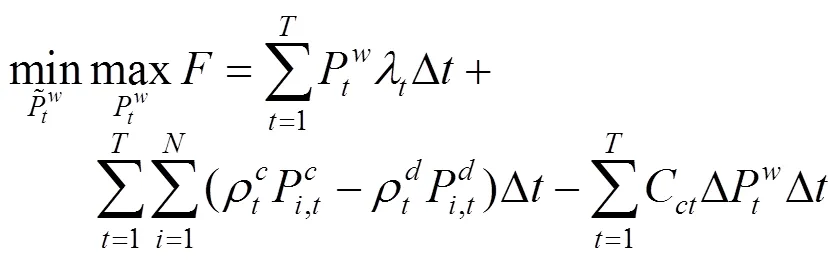
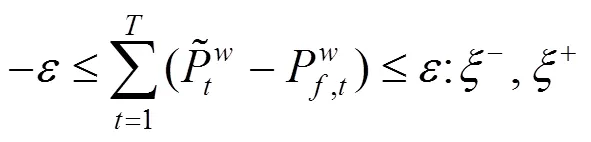
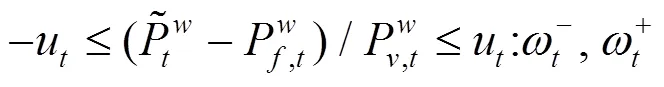
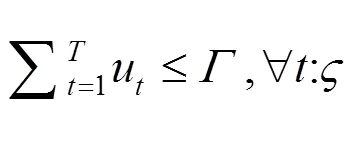
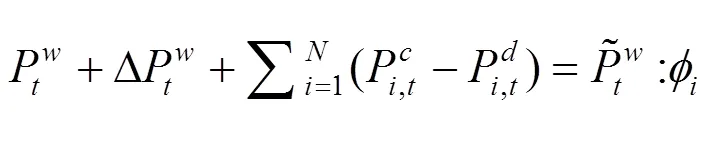
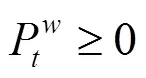
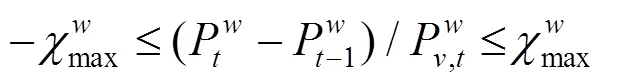
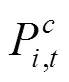
上述公式(3)—(10)中，目标函数式(3)极小化极大化风电场的收益，即考虑在最差情况下收益最大化的决策。风电场的收益由3部分组成，其中第1项代表向批发市场出售风电的收入；第2项为电动汽车用户支付给风电场的电费收入，包括充电成本和放电补偿费用；第3项为风电场的弃风成本。式(8)是有功率平衡约束。式(9)是风电运场日前投标出力上下限约束，表明风电场在日前市场的投标出力必须大于或等于0，投标为0表明该时段不参与市场发电。式(10)为风电场输出功率波动上下限约束。

2）下层优化模型。

下层决策者电动汽车的充放电功率优化问题如下：

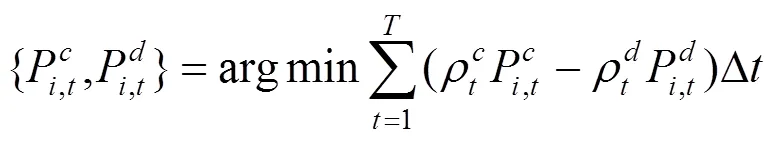
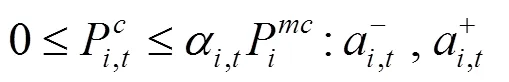
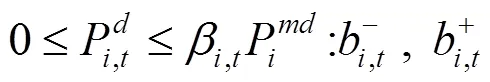
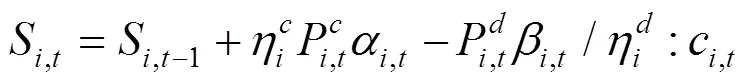
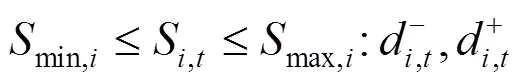
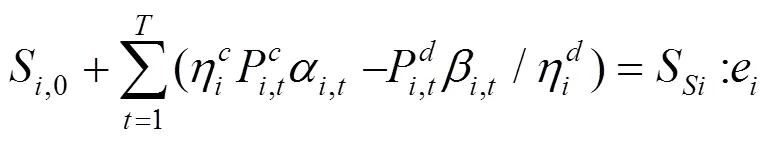
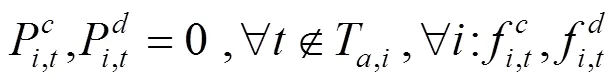
上述公式(11)—(17)中，目标函数式(11)表示在风电场给出的充放电价格下极小化自身电费支出成本；式(12)、(13)表示各辆电动汽车充放电功率上下限；式(14)、(15)为荷电状态约束，为了减小充放电对车载电池寿命的影响，需对电池的荷电状态加以约束；式(16)表示电动汽车用户出行需求约束，即电动汽车作为用户出行交通工具，在对其进行充放电控制的时候首先要考虑满足用户的出行需求；式(17)是电动汽车用户充放电状态约束，风电场只在T,i时段内对电动汽车进行充放电控制。

风电场优化问题式(3)—(10)和所有电动汽车优化问题式(11)—(17)构成了主双层优化模型，该模型最初由Stackelberg在文献[19]中提出，并在文献[20]中给出了上下层模型均为线性时的求解方法。下文基于对偶理论和Karush-KuhnTucker (KKT)条件将式(3)—(10)、(11)—(17)转化为混合整数线性规划，从而可以采用高效商业求解器CPLEX 12.2对模求出全局最优解，即上下优化问题的均衡点。

3 鲁棒优化模型的转换及其求解

3.1 上层优化模型的对偶转换

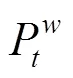
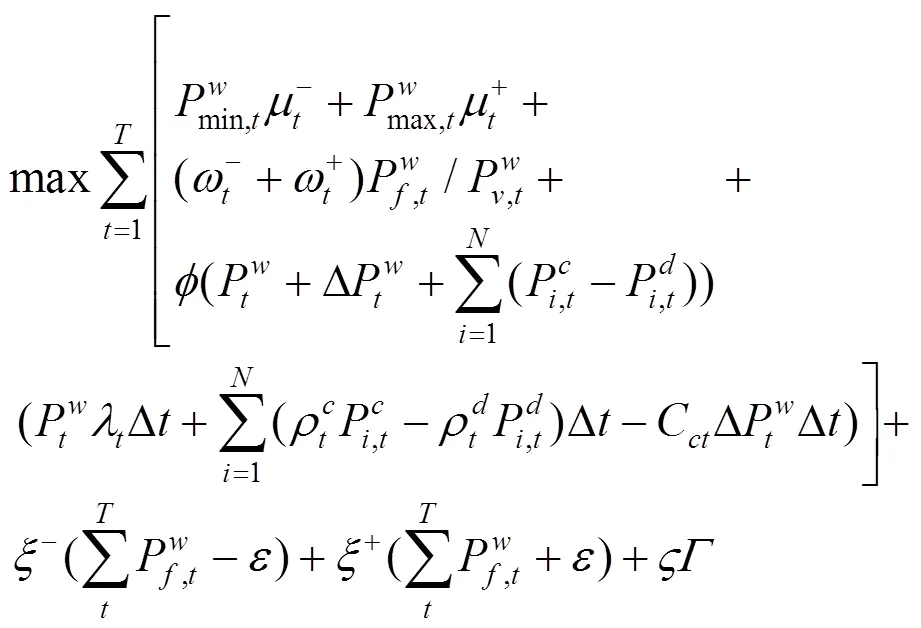
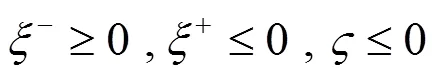
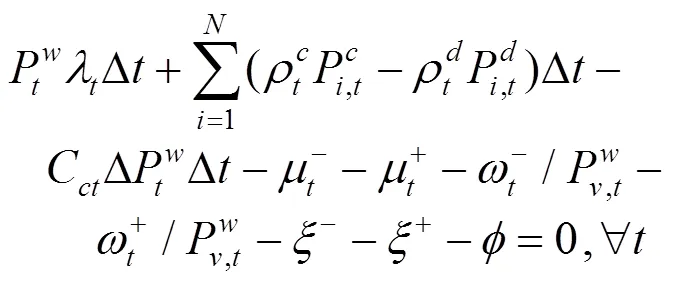
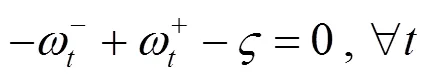
约束条件同公式(9)、(10)。

由式(18)—(22)可以看出，原上层模型经对偶转换后变成一个线性规划问题，从而简化了模型的求解。

3.2 下层优化模型的KKT转换

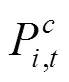
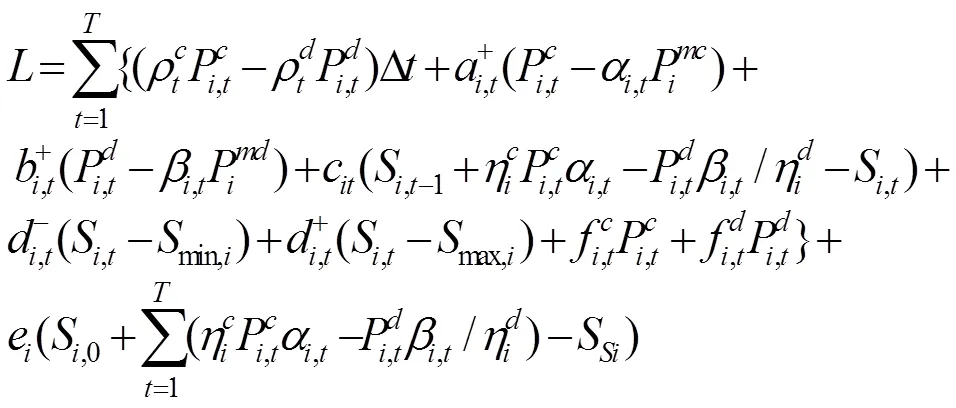
通过KKT条件将下层优化模型转化为下列约束条件：

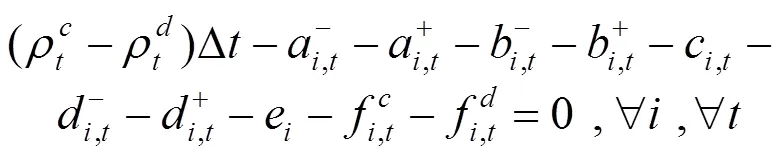
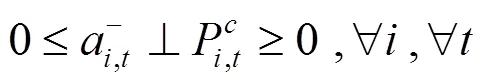
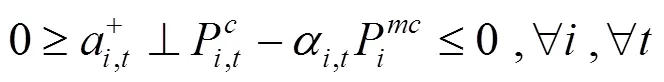
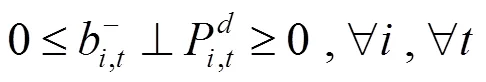
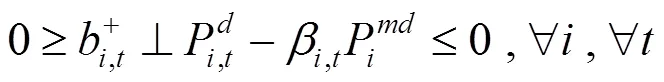
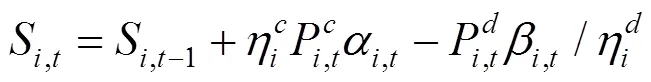
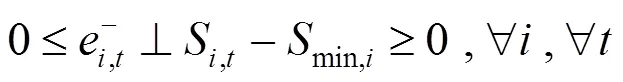
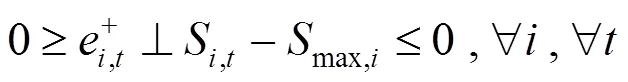
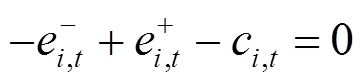
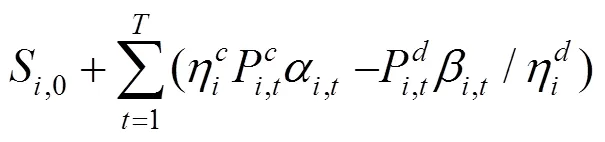
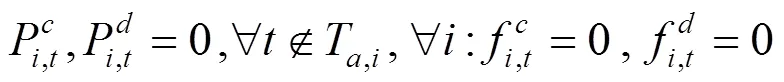
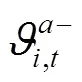
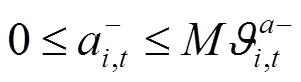
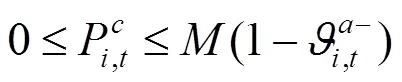
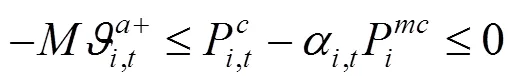
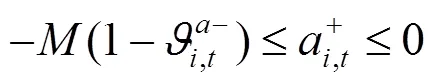
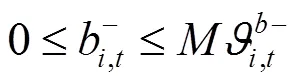
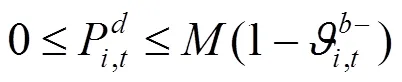
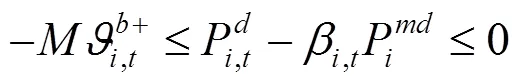
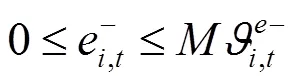
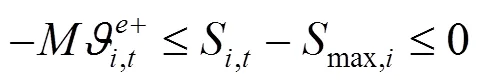
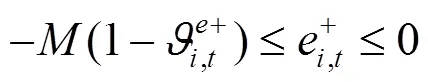
综上所述，风电场优化调度模型可转化为如下混合整数线性规划：

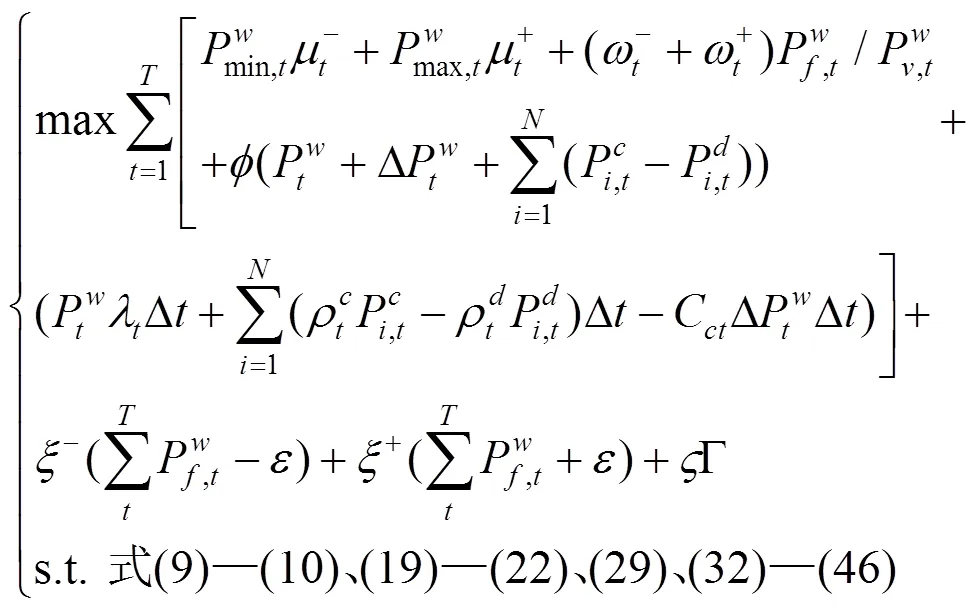
4 算例分析

4.1 上参数设置

本文研究的风电场主要包括：8台额定功率为2 MW的风电机组，300辆电动汽车。假设风机出力服从形状参数为2.15，尺度参数为14.99的Weibull分布，采用蒙特卡洛抽样的方法对风电出力的随机性进行模拟，抽样次数为5000次，图2给出了风电出力均值波动曲线图。为了方便显示计算结果，假设等值聚类后电动汽车可分为3组[22]，各组有=[90,140,70]辆电动汽车，各组电动汽车最小荷电容量均为9 kW×h，离网荷电容量均为35 kW×h，最大充放电功率均为4.5 kW，充放电效率取0.9。各组电动汽车并网充放电时间如表1所示，其中1为电动汽车接入电网时间段，0为电动汽车离网时间段。根据电动汽车行驶特性，把早出晚归的作为第1组(工作时间06:00—20:00)，正常工作时间的作为第2组(工作时间08:00—17:00)，夜间工作时间的作为第3组(工作时间20:00—06:00)。这里设置第1组为主要类型。

按照《GB/T 19963—2011风电接入电力系统技术规定》对风电并网运行时输出功率变化量的规定，要求装机容量小于30MW的风电场有功功率波动应小于20%。日前市场电价、电动汽车充放电电价见表2。风电场为激励电动汽车用户参与风电功率调节，电动汽车的充电价格一般制定的比市场电价略低，电动汽车的放电价格一般制定的比市场电价略高。

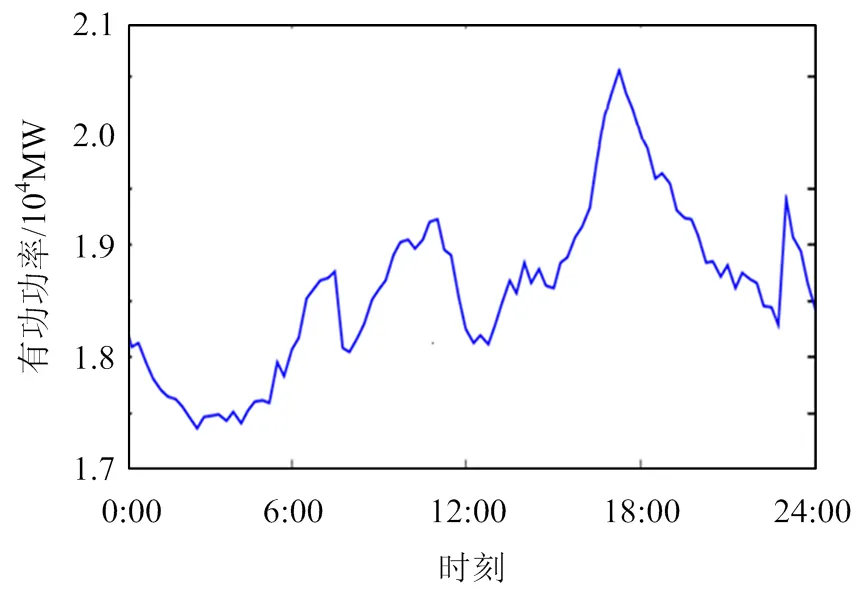
图2 风电出力均值

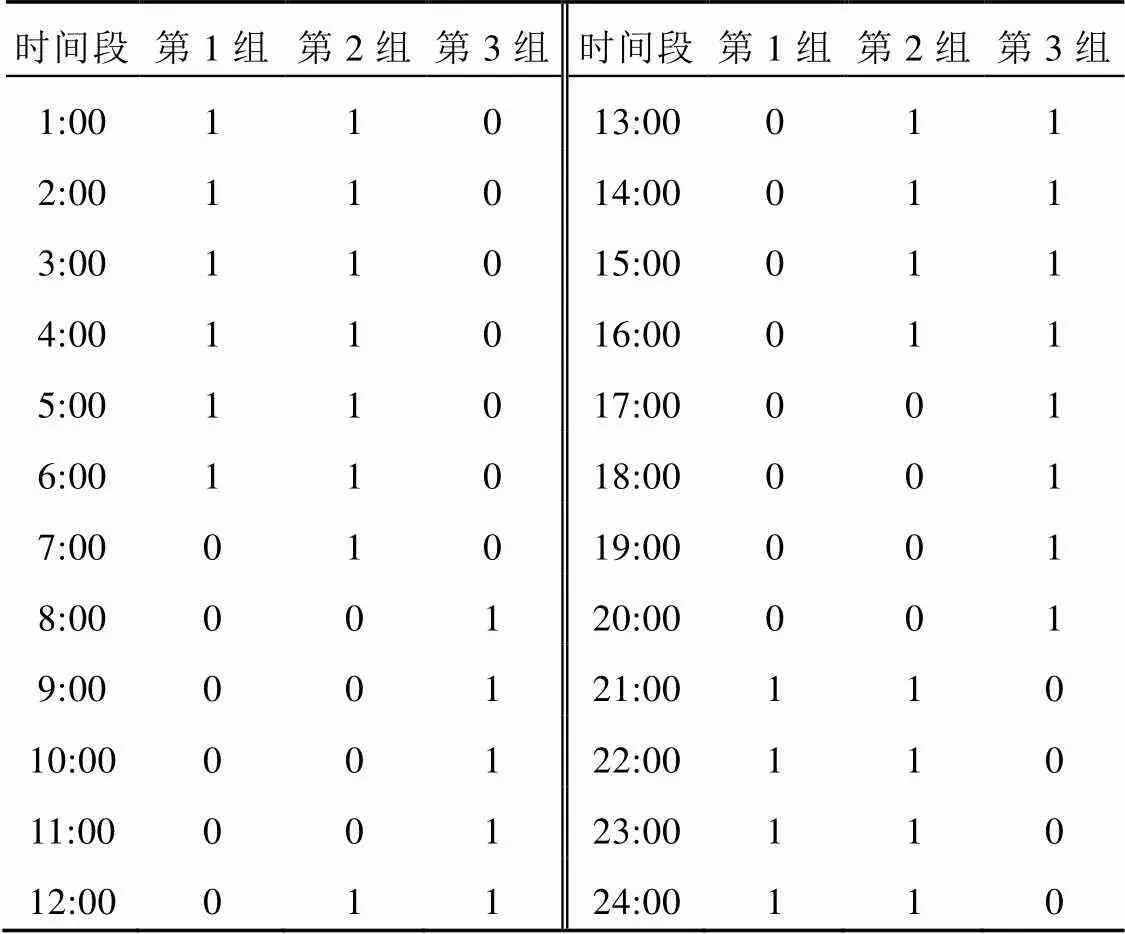
表1 不同组的电动汽车充放电时间段

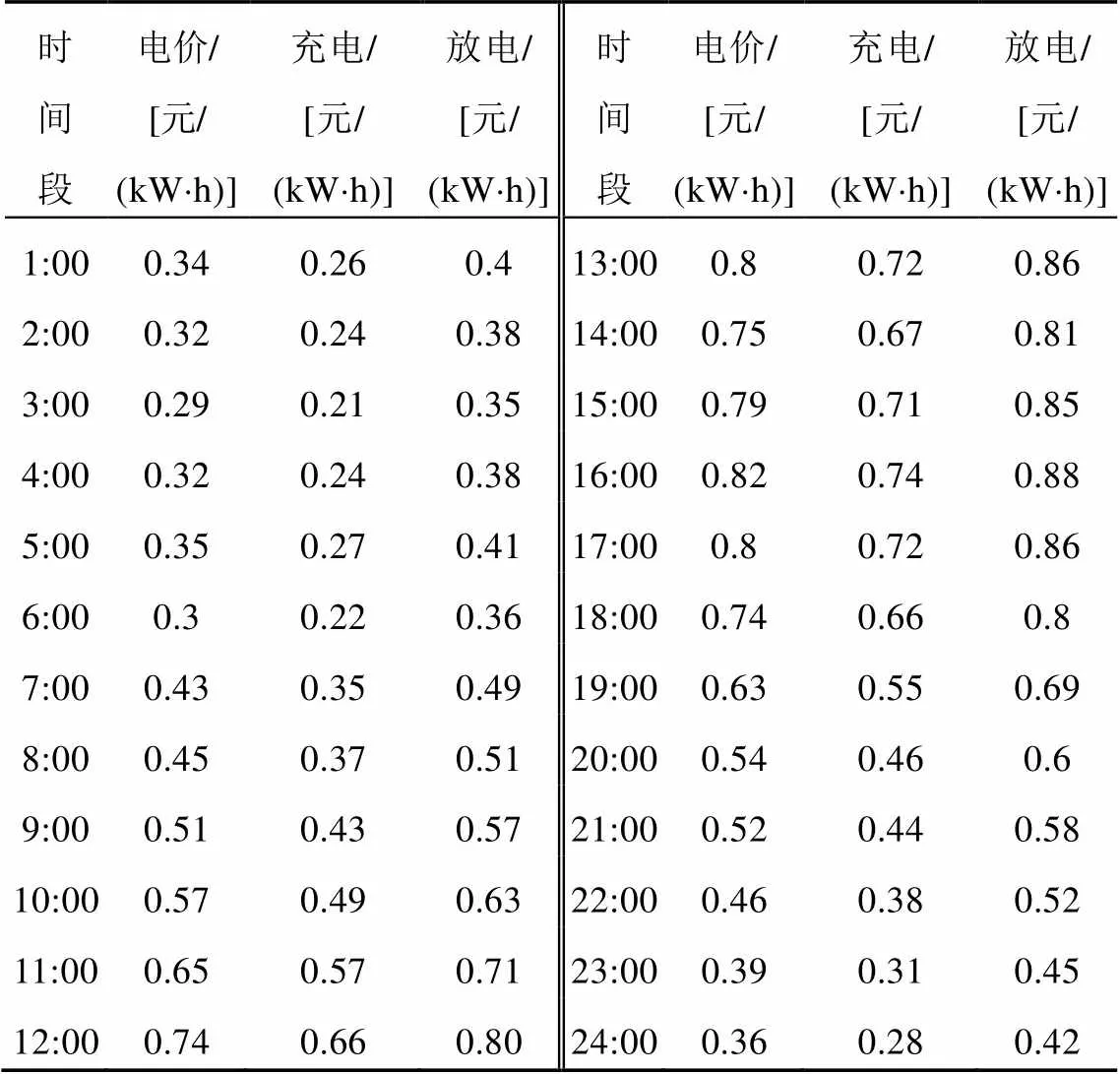
表2 日前市场电价、电动汽车充/放电电价

4.2 电动汽车配置比对优化结果的影响

在保证3组电动汽车总数量不变的前提下，改变各组中电动汽车的数量，所得优化结果见 图3。对比分析图3中风电场收益可以发现，在电动汽车配置比4=[90,140,70]下，风电场电收益最大，电动汽车配置比1=[0,0,300]时，风电场售电收益最小。这是因为配置比1下电动汽车主要为夜间行驶，白天并网充放电，而风电出力主要集中在夜晚，且夜间风电出力波动比较剧烈，因此配置比1下风电场晚上弃风最严重，相应弃风成本增加，从而导致风电场售电收益最低；配置比2、3下风电场收益比配置比1下风电场收益高，因为配置比2、3类型电动汽车主要并网充放电时间为夜晚，风电场弃风量少，能够较好地平抑夜间风电场输出功率波动；配置比3比配置比2类型电动汽车夜间并网充放电的时间长，所以配置比3比配置比2类型电动汽车风电场的售电收益要高；而在电动汽车配置比4下一天中各时段都有电动汽车并网充放电，且在夜晚时段电动汽车接入数量较大，能够有效平抑风电场一天当中各时段输出功率波动，降低了弃风成本，从而该配置比下的售电收益最大。

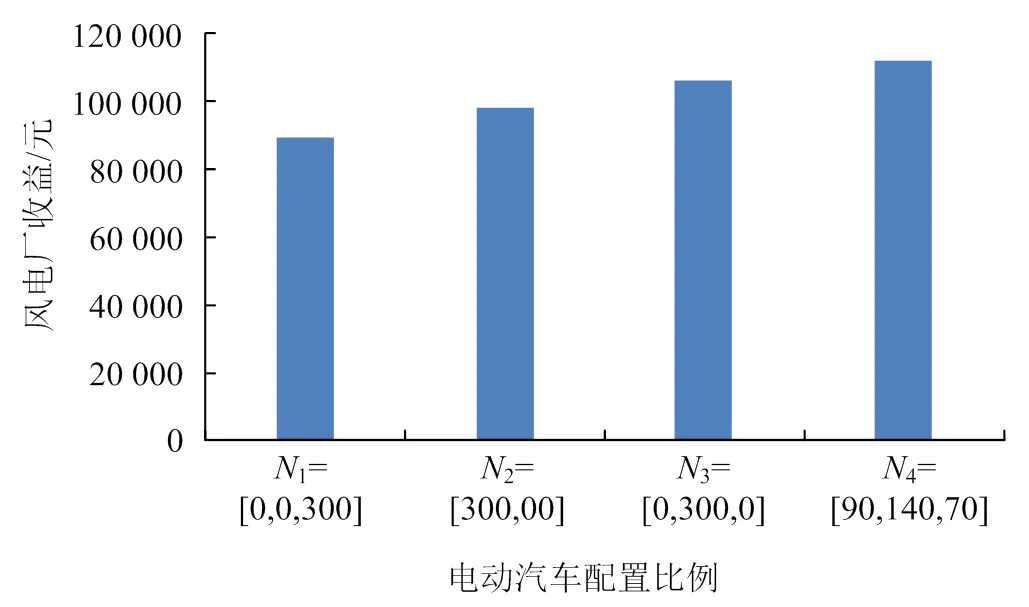
图3 不同电动汽车配置比例下风电场售电收益

为分析电动汽车参与风电场输出功率调节给自身带来的收益，图4给出了电动汽车直接从批发市场购电成本和由风电场代理其参与批发市场购电成本情况。由图4可以看出，在各电动汽车配置比下车主向风电场购电成本均低于直接向批发市场购电成本。同时，在电动汽车配置比例为1时，直接向批发市场购电成本与向风电场购电成本的差值比较小。这是因为该配置比例下由“夜间型”电动汽车为主，该类型电动汽车主要并网时间为白天，而白天时间风电功率波动较小，电动汽车参与风电场输出功率调节的效果也较差，因此获得的充放电补偿也相对较低，所以充电成本与直接从批发市场充电成本相差不大。然而，直接从批发市场购电成本仍是高于车主的充电成本，所以，车主参与风电场的功率调节仍是受益的。

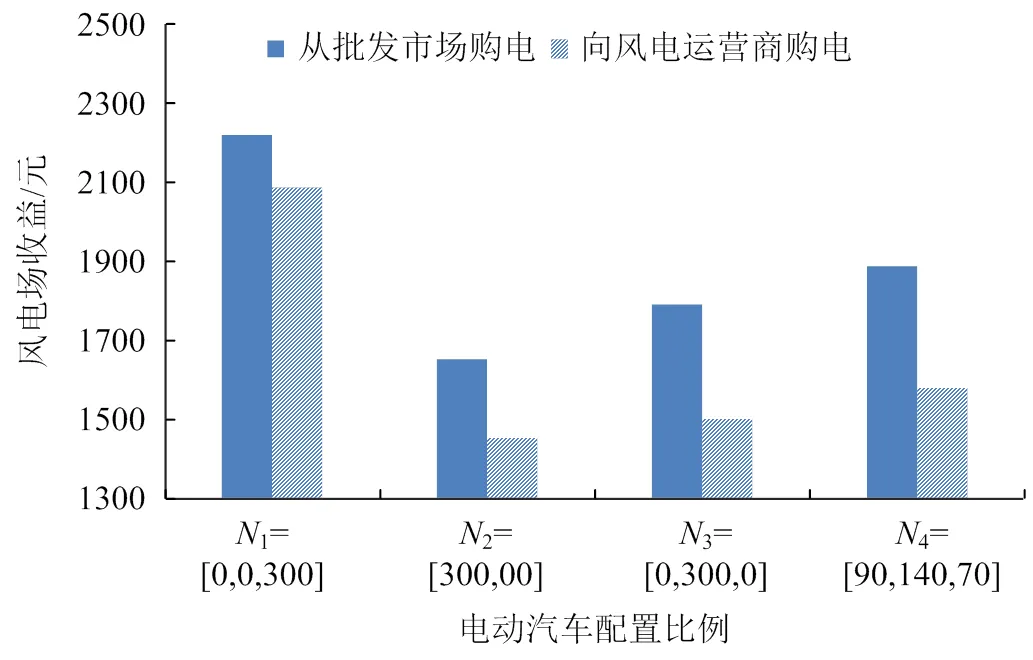
图4 不同电动汽车配置比例下充电成本对比

4.3 鲁棒控制系数对优化结果的影响

本文定义弃风改善率以反映电动汽车接入后的弃风改善情况，其具体表达式为

式中：N为电动汽车接入前调度周期内风电场弃风总量；Y为电动汽车接入后调度周期内风电场弃风总量。该指标描述了电动汽车接入后增加的风电并网总量占初始弃风总量的比例，该值越大表示电动汽车改善弃风效果越为显著。

图5给出了鲁棒控制系数在0~24范围内不同电动汽车配置比下的弃风改善率。由图5可以看出，当电动汽车配置比例一定时，随着鲁棒控制系数的增加，弃风改善率呈减小趋势。这是因为鲁棒控制系数取值越大，表明风电功率波动越剧烈，由于电动汽车调节能力有限，因此越恶劣情况下风电场弃风现象越严重，对应的弃风改善率降低。虽然鲁棒控制系数取值越小，风电场通过电动汽车调节输出功率波动效果越好，但在取值较小下得到调度方案将使风电场在最恶劣情况发生时面临的风险变大。这是因为取值越小，风电场的经济性固然越好，但是鲁棒性较差，不利于系统安全可靠运行。因此，风电场需根据实际运行情况合理的选择鲁棒控制系数，从而实现最终决策的经济性与安全性平衡。

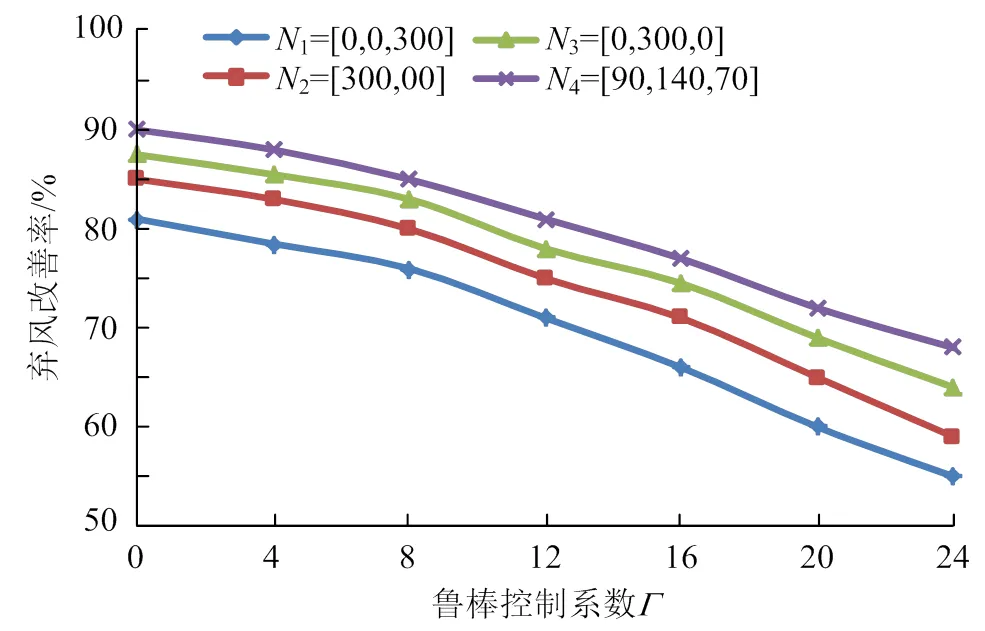
图5 不同鲁棒控制系数下弃风改善情况对比

5 结论

以含电动汽车的风电场为研究对象，分析了电动汽车参与调度对风电场并网功率的影响。结论如下：

1）由于风电出力具有较强的随机性、波动性，其概率分布难以被准确刻画，文中基于鲁棒优化的方法处理风电出力的不确定性，即将不确定的风电出力限定在一个确定的区间内，并引入鲁棒控制系数来调节不确定集合的区间大小，从而得到具有不同保守程度的优化决策方案。

2）构建的风电机组和电动汽车协调控制的双层优化模型：上层优化模型决策者是风电场，以风电场收益最大化为目标函数；下层优化模型决策者是电动汽车车主，以电动汽车电费支出成本最小化为目标函数，综合考虑了电动汽车用户出行需求和电费支出满意度。另外，还进一步通过线性规划对偶定理和KKT最优性条件将此鲁棒优化模型转化为混合整数线性规划问题进行 求解。

3）算例分析结果表明，将电动汽车作为可移动的储能装置，用来平抑风电出力波动，可有效降低弃风量，缓解风电出力不确定性对电网安全运行的影响；风电场可根据自身风险偏好，调整鲁棒控制系数，从而得到兼顾经济性和安全性的决策方案。

4）应用电动汽车平抑风电场输出功率的波动，其目的仅仅是为了满足系统的调频要求，在实际应用中需要将风机电动汽车联合的输出功率作为负的负荷，加到原始负荷中去，综合风电功率和负荷功率的波动趋势，得到最优的调度方案，因此，作者将在后续的工作中对这方面内容作进一步研究。

[1] 申宽育．中国风能资源与风力发电[J]．西北水电，2010(1)：76-81．

[2] 韦东远．世界风电产业发展趋势[J]．东北电力技术，2009(3)：37-40．

[3] 薛禹胜，雷兴，薛峰，等．关于风电不确定性对电力系统影响的评论[J]．中国电机工程学报，2014，34(29)：5029-5040．

[4] 刘文颖，文晶，谢昶，等．考虑风电消纳的电力系统源荷协调多目标优化方法[J]．中国电机工程学报，2015，35(5)：1079-1088．

[5] Eorgilakis Pavlos S．Technical challenges associated with the integration of wind power into power systems[J]．Renewable and Sustainable Energy Reviews，2008(12)：852-863．

[6] Yang T C，Yue D，Xin H H．On embedded energy storage for high penetration of wind power[J]．Wind Engineering，2008(32)：223-242．

[7] 杨水丽，惠东，李建林，等．适用于风电场的最佳电池容量选取的方法[J]．电力建设，2010，31(9)：1-4．

[8] Yoshida Y，Wu Guohong，Minakawa T．Mitigating fluctuation of wind turbine power generation system by introduction of electrical energy storage with combined use of EDLC and lead acid storage battery [C]//International Conference on Power System Technology，IEEE，2010：1-7．

[9] 陈厚合，杜欢欢，张儒峰，等．考虑风电不确定性的混合储能容量优化配置及运行策略[J]．电力自动化设备，2018，38(8)：174-182．

[10] 雷珽，欧阳曾恺，李征，等．平抑风能波动的储能电池SOC与滤波协调控制策略[J]．电力自动化设备，2015，35(7)：126-131．

[11] 颜伟，吕冰，赵霞，等．含高渗透率风电配网中电池储能系统和开关的协调规划[J]．电力自动化设备，2015，35(3)：6-11．

[12] 毕大强，葛宝明，王文亮，等．基于钒电池储能系统的风电场并网功率控制[J]．电力系统自动化，2010，34(13)：72-78．

[13] Wang Wenliang，Ge Baoming，Bi Daqiang，et al．Grid-connected wind farm power control using VRB-based energy storage system[C]//IEEEEnergy Conversion Congress and Exposition，2010．

[14] 谢应昭，卢继平，翁宗林，等．改善风电输出功率特性的复合储能系统优化配置[J]．电网技术，2016，40(7)：2052-2058．

[15] 孙国强，袁智，耿天翔，等．含电动汽车的虚拟电厂鲁棒随机优化调度[J]．电力系统自动化，2017，41(6)：44-49．

[16] 卢志刚，王荟敬，赵号，等．含V2G的虚拟电厂双层逆鲁棒随机优化调度策略[J]．电网技术，2017，41(4)：1245-1252．

[17] 庞明，史仪凯，袁小庆，等．平抑风电功率波动混合储能系统容量优化方法[J]．西北工业大学学报，2016，34(3)：493-498．

[18] Wei W，Liu F，Mei S．Energy pricing and dispatch for smart grid retailers under demand response and market price uncertainty[J]．IEEE Transactions on Smart Grid，2015，6(3)：1364-1374．

[19] Stackelberg H V．Marktform Und Gleichgewicht [M]．Vienna：Springer，1934．

[20] Anandalingam G，White D J．A solution method for the linear static Stackelberg problem using penalty functions[J]．Automatic control IEEE Transactions on，1990，35(10)：1170-1173．

[21] Fortunyamat J，Mccarl B．A repressentation and economic interpretation of a two-level programming problem[J]．Journal of the Operational Research Society，1981，32(9)：783-792．

[22] 魏韡，陈玥，刘锋．基于主从博弈的智能小区代理商定价策略及电动汽车充电管理[J]．电网技术，2015，39(4)：939-945．

Research on the Method of Stabilizing the Power Output Fluctuation of Wind Farm by Electric Vehicles

CHEN Yu1, PENG Xiao2, DING Jing3, WANG Yazhou1, SHAO Jingping1

(1. Hubei Huadian Xisaishan Power Generation Co. LTD, Huangshi 435001, Hubei Province, China; 2. State Grid Hubei Electric Power Co., LTD, Jingzhou City Jingzhou District Power Supply Company, Jingzhou 434000, Hubei Province, China; 3. State Grid Hubei Electric Power Co., LTD, Ezhou City Echeng District Power Supply Company, Ezhou 436000, Hubei Province, China)

Owing to the inherent randomness and intermittency of wind power, the output power of wind farm tends to fluctuate greatly. However, considering the high cost of energy storage device, it is not good for the wind farm to configure energy storage device. This paper studies the fluctuation of output power fluctuation in the wind power field considering the participation of electric vehicles. Firstly, according to the requirement of the national standard of stroke, "active power change", the rate of output power of wind farm is described by the concept of climbing rate. Then, using the robust optimization method to deal with the uncertainty of wind power, wind turbines and electric cars, coordinated control of bi-level optimization model: the upper model decision makers is a wind farm, with wind farms sell electricity utility maximization as the objective function; The lower-level model decision makers are electric car owners, and the cost of electric power costs is minimized to the target function. In addition, this robust optimization model is transformed into a hybrid integer linear programming problem by using the linear programming dual theorem and Karush-Kuhn Tucker (KKT) optimality conditions. Finally, the effectiveness of the proposed model and method is verified by simulation.

wind farm; electric vehicle; power fluctuation; robust optimization; double layer optimization

10.12096/j.2096-4528.pgt.18151

2018-10-09。

陈宇(1995)，男，硕士，研究方向为电力系统继电保护，815034513@qq.com。

陈宇

(责任编辑 杨阳)