对一道解析几何联考题解法的探究与拓展

■安徽省阜阳市太和中学 任海涛

一、题目呈现

试题:(2018年安徽省江南十校联考题第20题)A、B、C、D是抛物线E:x2=2p y(p＞0)上的四点,A、C关于抛物线的对称轴对称且在直线B D的异侧,直线l:x-y-1=0是抛物线在点C处的切线方程,且B D∥l。

(1)求抛物线E的方程。

(2)求证:A C平分∠B A D。

二、题目分析与解法

本题是一道解析几何综合题,以直线和抛物线为载体,主要考查抛物线的方程和性质,以及直线和抛物线的位置关系等基础知识,又考查了数学基础知识和基本技能。本题贴近学生实际,既注意全面,又突出重点,注重对知识内在联系的考查,注重对中学数学中所蕴含的数学思想方法的考查。本题考查了同学们的抽象概括能力、运算求解能力、推理论证能力及分析问题与解决问题能力,也有效考查了同学们的数学核心素养。

(1)试题第一问考查抛物线的切线问题,既可以从切线的求法入手,也可以从直线和抛物线的位置关系入手,从而得到如下解法:

因为直线l:x-y-1=0是抛物线在C处的切线方程,且直线B D∥l,所以利用切点的性质可得

所以抛物线的方程为x2=4y。

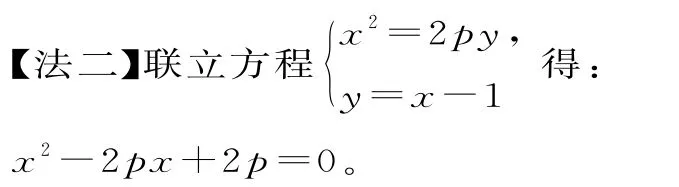
因为直线l:x-y-1=0是抛物线在C处的切线方程,所以Δ=0,解得p=2或0(舍去)。

所以抛物线的方程为x2=4y。

(2)第二问考查了直线与抛物线的位置关系,在研究A C平分∠B A D时,要善于从数和形两个角度出发,注重平面几何知识的渗透,解析几何首先是几何问题,一味强调解析几何中的代数运算有时会导致烦琐的运算过程,在解题时要综合考虑几何因素,即在用代数方法研究曲线间关系的同时,注意利用好图形本身所具有的平面几何知识,从而得到不同的解法。

由(1)可知C(2,1),A(-2,1)。

因为B D∥l,所以B D的方程可设为y=x+t。

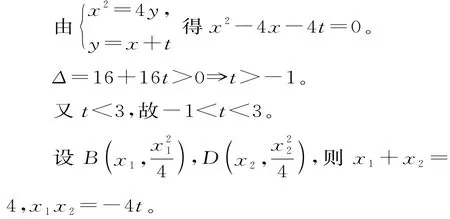
【法一】A、C关于抛物线的对称轴对称,故A C∥x轴。要证A C平分∠B A D,不妨从斜率入手,证明:kAD+kAB=0。

证明如下:

【法二】要证A C平分∠B A D,可以从角平分线的性质入手,只需证点C到∠B A D两边的距离相等。

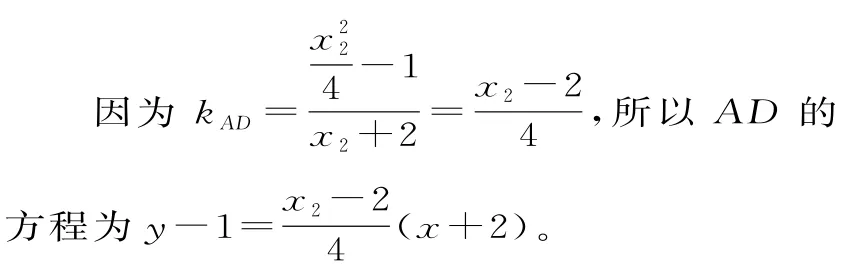
化简即为(x2-2)x-4y+2x2=0,所以点C到直线A D的距离为:

同理可得点C到直线A B的距离为d2=

因此,A C平分∠B A D。

【法三】要证A C平分∠B A D,可以从向量的角度入手。

因此,c o s∠DA C=c o s∠B A C,∠DA C=∠B A C,A C平分∠B A D。

【法四】从图形的对称性入手,要证A C平分∠B A D,只需证明点B关于A C的对称点在直线A D上,由法二知:A D的方程为(x2-2)x-4y+2x2=0。

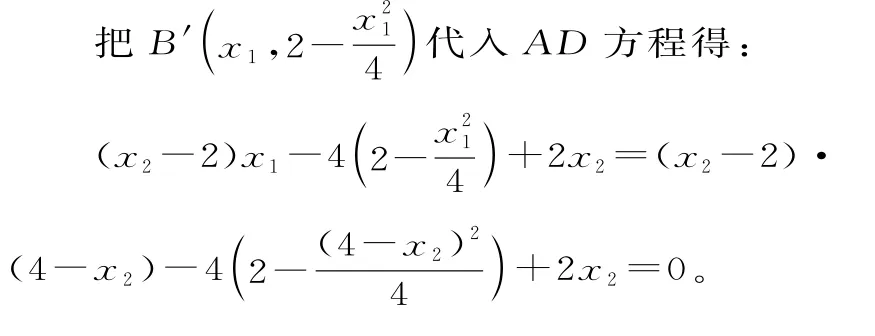
故A C平分∠B A D。

三、题源剖析

本题具有初等几何的背景,圆有性质:圆的圆心必在切线夹角的平分线上。

类比到圆锥曲线中,可得到性质:过圆锥曲线外一点作圆锥曲线两切线与焦点连线所成的角相等(抛物线可看成另一焦点在无穷远处)(以椭圆为例证明)。

证明:设P(x0,y0),A(x1,y1),B(x2,y2)。

四、命题拓展

圆锥曲线的切线作为和圆锥曲线位置关系最特殊的直线揭示了直线和圆锥曲线位置关系中定性的结论和几何性质的不变性。将上述性质进行推广,可以得到以下性质:

性质2:已知点B(-m,0)(m＞0),设不垂直于x轴的直线l与抛物线y2=2p x(p＞0)交于不同的两点P、Q,若x轴是∠P B Q平分线⇔直线l过定点(m,0)。

性质3:已知点B(m,0)(|m|＞a),不垂直于x轴的直线l与椭圆交于不同的两点P、Q,则x轴是∠P B Q平分线⇔直线l过定点

同学们解题时需要从形式的“变”发现本质的“不变”,从本质的“不变”探索形式的“变”的规律,发现知识的横向联系,揭示其内在的联系与规律,从中提炼出数学思想、数学方法,领悟思维的诱导、调整、进阶、完善,重新全面梳理知识、方法,注意知识结构的重组与概括,精学一题、妙解一类,固化于形、内化于心,进而形成一个有序化、条理化、网络化的高效的有机认知结构,从而有层次地、递进地理解数学本质,从而提升大家的数学思维素养。