异点双站测高在超高建筑验收测量中的应用

李会林

(珠海市测绘院，广东 珠海 519000)

1 引 言

三角高程测量以其方便高效性[1，2]，广泛应用于测绘和建设工程领域[3]。随着测边、测角精度的提高，目前全站仪三角高程测量可以代替四等水准测量[4]，甚至是更高等级的水准测量[5，6]。三角高程测量是一种间接测量方法，其优点不受地形的限制，当高差较大时，比水准测量更简便快速，因此在建筑施工测量中，全站仪三角高程测高应用屡见不鲜[2]。随着国家经济的高速发展，近年来超高层建筑不断涌现，传统的钢尺量距规划验收测量方法在应用时受到一定限制，且规划验收测量不仅要求测定整栋建筑物的高度，还要求测定每层建筑物的高度，因此钢尺量距增加了竖向定线误差，同时由于多测段误差积累，易造成超高建筑物总高度误差增大，因此如何采用合适的替代方法，有效提高观测效率和精度成为测绘工作者所要解决的关键问题。针对这个问题，本文提出了一种异点双站超高建筑物测高方法，并与传统无定线钢尺测高法、有定线钢尺测高法相比，得出了较为满意的高程测量精度。

2 异点双站建筑物测高

2.1 单站三角高程测高

全站仪三角高程测量主要用于四、五等高程控制，在地形起伏较大、地区范围比较小的情况下非常适用。三角高程测量依据的是三角形几何边角关系，如图1所示，若A为已知高程控制点，其高程为HA，在A点架设全站仪，量取仪器高i，中丝瞄准目标M，测得竖直角为α，A到B的水平距离为D，根据高差关系，A到B的高差为hAB=Dtanα+i-v，因此B的高程计算公式如式(1)所示，当D>300 m时，需加上球气差近似改正数[7]，其中R为地球平均曲率半径。

(1)

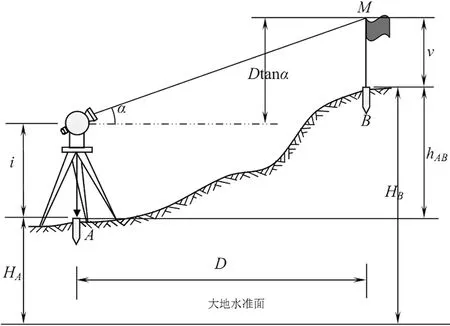
图1 全站仪三角高程测量原理

在超高层建筑测高时，建筑物高度是依据底点和顶点高差计算的，假设测站仍为A，底点为B1，顶点为B2，建筑高为H，则H=HB1-HB2，本文基于这个原理提出一种异点双站测高方法，减小已知点误差的影响，提高测高精度。

2.2 异点双站测高

异点双站测高是在两个测站分别架设全站仪(或经纬仪)，通过测定标示建筑物顶底垂线的两点高程，求取其高差作为超高层建筑物高度。如图2所示，分别在测站A、B架设全站仪，通过测定建筑物高度垂线顶底C1、C2高程，取其差分别作为A、B点各自获取的高度，再对A、B点获取的高度取平均数，获取建筑物最终高度。实际观测时，A、B点之间互不后视，而是分别选用不同的后视点M、N，可使楼高测量与建筑物平面坐标测量同时进行，可有效减小由A、B点定向误差引起的坐标误差，使平面坐标测量精度趋于均匀。

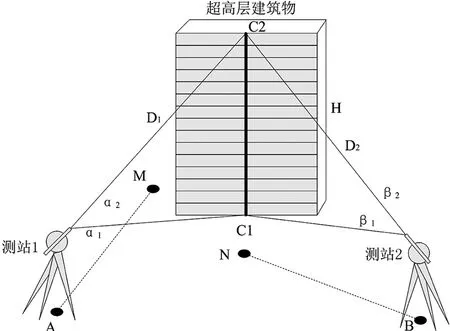
图2 异点双测站超高层建筑物测高

(2)

2.3 异点双测站测高精度估计

超高层建筑一般均为几百米，受竖直角观测限制，对应的水平距离一般也较大，多数情况大于 300 m，因此式(1)、式(2)的(b)式具有实际应用意义。根据误差传播定律，函数中误差平方等于观测值中误差偏导数与该项中误差积的平方和，因此式(1)(b)产生的误差为：

带入偏导数计算值，所得单点高程中误差为：

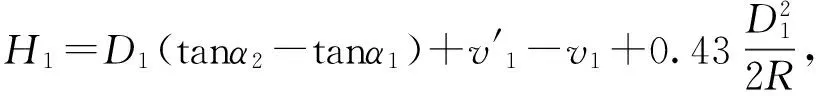
由算数平均值中误差公式，易推得异点双站测高中误差如式(3)所示。

(3)

式(3)表明使用一定测边、测角精度的仪器进行异点双站测高时，就可估计测高中误差。假定楼高垂线底点方向水平角α1=0，不同垂线顶点α2及其对应的水平距离D1，观测全站仪精度为3+2 ppm，测角精度为2″，那么当水平距离为不同D1值时，mD1=3+2×D1(mm)，此时对应楼高误差估计如表1所示。

异点双站测高误差估计 表1

对于超高层建筑，其高度一般在 100 m～800 m之间，因此水平距离也大致在 100 m～800 m范围内，而观测竖直角可能是任意范围，但从表1看来，异点双站测高误差可以控制在 4 mm以内。进一步分析表1可知，竖直角值大小对测高误差影响较为明显，当竖直角大于65°时，误差增大较快，而测距误差对测高精度影响极小，另外测量仪器的标称精度对测高影响也很小，此两项误差可以忽略不计，因此异点双站测高具有较高的理论精度。

3 实验与分析

3.1 实验工程

实验工程选取两个典型超高层建筑物作为测高对象。第一个建筑物是珠海天朗海峰，该建筑分为A、B两座，建筑总层数65层，设计标高 185 m，其功能布置：三层地下室(停车场、人防等功能配置)；一至四层裙楼为商场；裙楼顶层以上2幢住宅塔楼，每幢塔楼58层(其中：塔楼1层为住宅入户大堂，2层为会所，3层为商业配套的办公楼层，第22层、第37层为避难层，其余的53个楼层均为住宅标准层)。第二个建筑是珠海中心大厦，其中地上65层，地下2层，设计标高 330 m，分为6个测高段，不包括地下层。实验选取的超高建筑如图3所示，其中珠海天朗海峰A、B座和珠海中心大厦均采用异点双站测高方法与传统方法施测。

图3 异点双站测高建筑物

3.2 超高层建筑测高

(1)精密钢尺测高

精密钢尺量距必须进行三项改正：尺长改正、温度改正和高差改正，对于操作严密的水平精密钢尺量距，其精度可达1/10000～1/40000[8]，但超高层建筑物测高一般难以控制，因此精度较水平测距有所降低。钢尺精密测定珠海天朗海峰A、B座时，施工时以核心筒分段高度进行精密量距，测量珠海中心大厦时，施工采用激光投点分层精密钢尺测距，实验中采用 50 m钢尺，其尺长方程如式(4)所示，其中l为尺长，l0为钢尺名义长度，△l0为整尺段尺长改正数，α为钢尺膨胀系数，本案中选取1.2×10-5/℃，t为实际温度，t0为钢尺检定时的标准温度，检定时压力为 100 N。

l=l0+△l0+αl0(t-t0)

(4)

(5)

实验中，每个高度均进行尺长改正、温度改正和高差改正三项改正[9]，改正数计算如式(5)所示，(a)、(b)、(c)分别为尺长改正、温度改正和高差改正，其中△l0=l′-l0，h为两端点高差，其他参数含义同上。与水平方向量距不同，高差h在垂向量距时需要归化改正，实验中采用的是坐标投点法，通过全站仪测定端点坐标，投影到水平面上，反算其距离，获得高差h。通过精密量距测高，测定珠海天朗海峰和珠海中心大厦分段高度如表2所示，对各测高段测距相对误差进行统计，得表3所示结果。

钢尺精密测距高度测量成果(单位/m) 表2

钢尺精密量距测高相对精度 表3

(2)无定线普通钢尺测高

无定线普通钢尺测高是在超高建筑主体完工后，沿着建筑物外缘垂线测定建筑物各段高度，测距时既不进行钢尺校正，也不进行改正数计算，且外垂线未经经纬仪或全站仪竖向定线。据此采用相同高段对珠海天朗海峰A、B座和珠海中心大厦进行测量，获取的高度测量成果如表4所示。

无定线普通钢尺测高成果(单位/m) 表4

(3)有定线普通钢尺测高

有定线普通钢尺测高通是过全站仪或经纬仪对建筑外缘垂线进行竖向定线，施测方法与无定线普通钢尺测高基本相同，据此对珠海天朗海峰A、B座和珠海中心大厦进行测量，测取的各测高段数据如表5所示。

有定线普通钢尺测高成果(单位/m) 表5

(4)异点双站测高

按照2.2所述方法，在珠海天朗海峰A、B座和珠海中心大厦周围布设的一级导线点与一级GPS点实施全站仪异点双站测高，选取建筑物顶底线与测站点通视，每次测取高段分界点的水平角和水平距离，按式(2)计算相邻点高差，最终确定测高段高度，所得高段测量成果如表6所示。

异点双站测高成果(单位/m) 表6

3.3 精度分析

将精密钢尺测高、无定线普通钢尺测高、有定线普通钢尺测高和异点双站测高分别命名为Ⅰ、Ⅱ、Ⅲ、Ⅳ，在这四种方法中，由于精密钢尺测高是在施工中分段测量的，且方法精密可靠，由表3分析知该法测量精度接近于1/10000，因此精密测量成果可以作为控制成果，其他测量成果与其比较，可以反映各种测距方法的优劣。以精密钢尺测高数据为准，计算无定线普通钢尺测高、有定线普通钢尺测高和异点双站测高三种方法各测高段相对精度和总高相对精度，可得如表7和表8所示的精度分析表。

测高方法相对精度比较 表7

注：此表中数值是相对误差分母，其值越大精度越高。

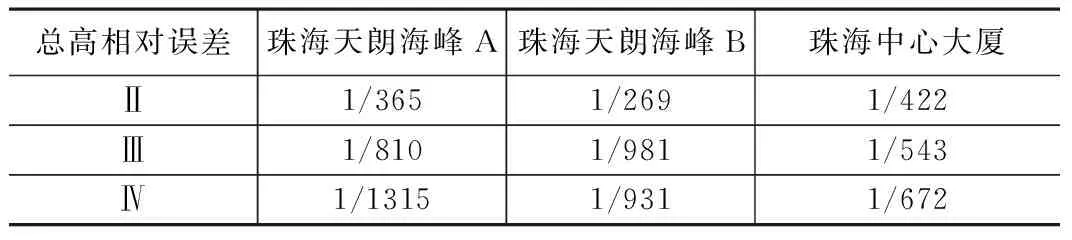
超高建筑总高相对精度 表8

分析表7发现，虽然无定线普通钢尺测高、有定线普通钢尺测高和异点双站测高相同测高段精度没有绝对规律，但总体上三种方法精度依次增高，异点双站测高具有最高的测量精度。分析表8可知，总高测量三种方法中异点双站测高精度最高，有定线普通钢尺测高次之，无定线普通钢尺测高精度最低，其中珠海中心大厦整体精度均不高，这与大厦侧面弧形设计有关，尤其是无定线普通钢尺测高，总高仅有1/422的相对精度，异点双站测高精度也仅达到1/672，这与理论估计相差较大，说明观测环境对超高层建筑测高精度具有较大影响。

在效率方面，无定线普通钢尺测高需要按照高段逐节观测，在观测长距离高段靠人工竖向定向，因此实施费力费时，效率较低。有定线普通钢尺测高虽然量距较前者有所提高，但需要全站仪或经纬仪竖向定线，增加工作环节，总体效率不优于无定线普通钢尺测高。异点双站测高仅需设置经纬仪或全站仪，观测量仅有水平距离和竖直角，观测时仅需全站仪或经纬仪合作目标，虽然实施中需要至少4个控制点，但在一般的建筑工程中，控制点数量和精度还是有保障的，因此异点双站测高是一种高效、简便、精度较高的超高层建筑物测高方法。

4 结 论

基于三角高程测量，本文提出了一种异点双站测高方法，该法在互不定向的相异两站测量高段顶底高程，通过求取其高差计算超高建筑物高度，理论上，本文提出的方法具有较高的精度，实际应用时其精度也高于无定线普通钢尺测高和有定线普通钢尺测高，尤其是异点双站测高可以大幅提高观测效率，因此是一种简单高效的超高层建筑物测高方法。然而，由于超高层建筑外形设计多样，而周围观测环境一般也比较复杂，因此在测定不规则超高建筑物时，其精度降低较为明显。后续研究应集中于不良观测环境精度改善，以提高其应用普适性。