数字正垂仪在日周期摆动监测中的应用

余凌燕，宋奇鸿

(广州市城市规划勘测设计研究院，广东 广州 510060)

1 引 言

近些年来，我国因为城市化的进程加快，超高层建筑的规模和数量都在不断地被刷新，其施工监测技术也在日趋成熟。日周期摆动监测作为超高层建筑施工监测技术体系的主要内容之一，对施工过程中可能存在的问题起到预警作用，也为施工基准网的竖向传递提供精确、科学的数学改正模型。

广州东塔位于广州天河区珠江新城CBD中心地段，与西侧的广州西塔、珠江对岸的广州电视塔(俗称“小蛮腰”)形成“三塔鼎力”之势，高度为 530 m，为华南地区第一高楼。建筑塔顶采取“之”字形的退台设计，在不同楼层形成空中花园；玻璃幕墙采用白色陶土板挂件，可以天然采光；结构上首次采取超高强绿色混凝土，有效减轻了自重，在建筑上具有显著特色。

2 数字正垂仪原理

数字正垂仪由武汉大学研制，通常用于大坝安全监测。[1]数字正垂仪监测系统由数据采集系统、数据传输系统、数据处理系统组成，正垂线仪由重锤、传感器的线圈和栅格板组成，线圈安装在重锤的下方，栅格板安置在观测点上。其中，数据传输系统由传感器、数据转换模块、控制计算机等组成。数据处理系统根据摆动方程实现快速数据提取、拟合，具有方便、快捷、精度高的特点。因为仪器采样速率高，重锤没有阻尼装置，通过对连续观测的数据进行数学处理，可以精确计算垂线的中心位置。

数字正垂仪安装时，首先需要在转换层的预留孔之间安装防风管，采用全站仪对正垂仪接收板进行定向，使正垂仪的X、Y方向与施工坐标系的X、Y方向相保持一致，即X方向为东西方向，Y方向为南北方向。安装完成后，对超高层建筑进行了连续日周期观测，在观测同时每隔一定时间测量风速与温度值，获取楼层之间相对摆动值，实现数据采集的自动化。

数字正垂仪垂线的线圈安装在重锤上，重锤处于自由摆动状态，它的摆动方程为：

xi=Ae-fticos(2πti/T+θ)+X

其中，xi为线圈中心相对于二维栅格的平面位置；A为垂线的摆幅；f为垂线摆动的衰减系数；T为垂线的摆动周期；ti为时间；θ为垂线的摆动初相角；X为垂线的摆动平衡值。由于系统有很高的采样速率，在很短的时间内，即可获得垂线的观测数据。在短时间内认为垂线的摆动是一个非衰减的自由摆，它的摆动方程为：

xi=Acos(2πti/T+θ)+X

在方程中有4个未知参数(A，T，θ，X)，只要观测4组数据(xi，ti)就可求解出唯一的解，采用最小二乘平差方法可求得多组观测值下的参数最大或然值，从而得到精确的垂线中心位置。

3 数字正垂仪在日周期摆动监测中的应用

数字正垂仪对超高层建筑进行了连续日周期观测，需要在观测同时每隔一定时间测量风速与温度值，获取楼层之间相对摆动值，实现了数据采集的自动化。具体如图1所示。

图1 数字正垂仪安装示意图

如图2所示，利用数字正垂仪对广州东塔主塔楼连续进行48 h观测，获取了70层相对于85层约 60 m高的楼体摆动值，整个观测过程中设置数据采样率为15 min，对48 h观测数据进行处理后，以观测值和均值的差值为纵轴，以采样时间为横轴，得到了一个日周期内观测数据的x坐标与y坐标变化曲线图：

整个观测过程中的温度和风速变化曲线图如图3所示：

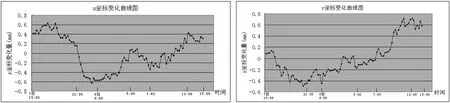
图2连续24小时观测数据的x坐标与y坐标变化曲线图

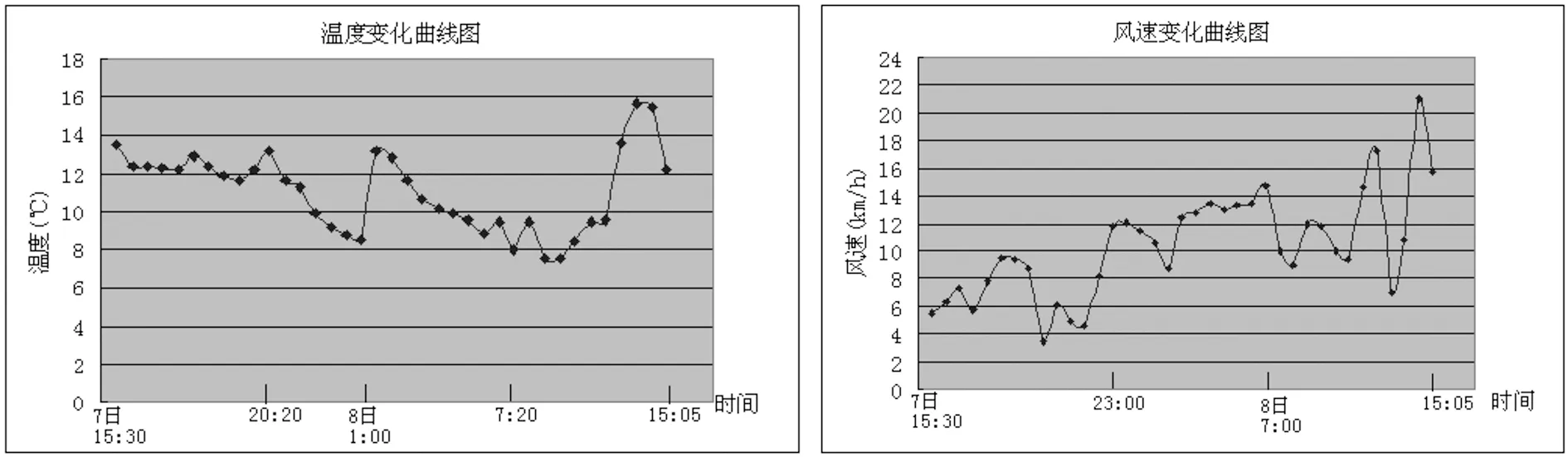
图3 连续24小时观测的温度及风速变化曲线图

由于观测数据序列中有用信号和噪声的时频特性通常是不同的，因此可以通过小波变换有效地分离出有用信号和噪声，实现消噪的目的。小波滤波所分离出的噪声实质上反映了变形监测的观测精度，由噪声量可以更为客观地评定监测系统的精度。

图4滤波前后的x、y坐标变化数据序列及残差图

如图4所示，通过采用小波变换进行滤波，得到滤波前后的x，y坐标变化数据序列及残差图(横轴为采样时间序列，纵轴为坐标变化量(单位：mm))。其中x，y方向的残差都不超过 0.2 mm，其中x方向为 0.20 mm，y方向为 0.15 mm，这说明采用数字正垂仪进行塔体的日周期摆动监测精度较高，技术手段合理，采样数据完全可以满足工程质量控制要求。

4 数据检核验证

4.1 GPS法检核

GPS法检核的主要思路是将转换层控制点通过竖向传递把其投到当前施工的最高层钢平台，在钢平台标志处架设GPS接收机，采用GPS静态测量的方式，与超高层建筑外围较为稳定的基准控制点进行联测，平差解算得到施工控制网点的绝对坐标，并与数字正垂仪系统监测数据进行比较，如图5所示。

图5 钢平台GPS接收机复测现场

广州东塔监测对施工内、外控制网复测4次(50层外控网、70层内控网、85层内控网和103层内控网)，复测结果和数字正垂仪系统监测得到的变形轨迹对比如表1所示：

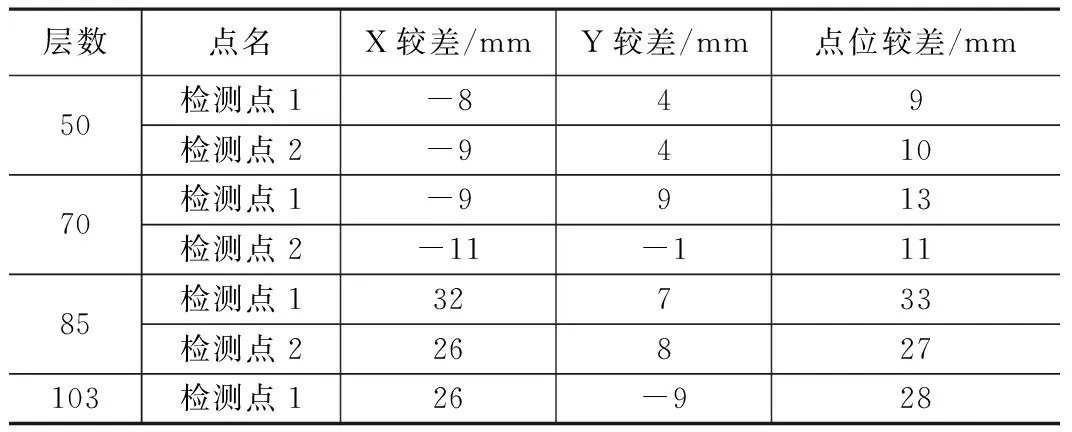
钢平台GPS复测结果 表1

结果表明，数字正垂仪监测系统和GPS法测得主塔楼摆动方向和数字偏差基本一致。以70层至85层数字正垂仪观测结果推算：该段高差 58.5 m，最大摆幅为 4.2 mm，假定塔体变化的规律是线性的，则可推算85层最大摆幅为(4.2/58.5)×364.5=26 mm，103层最大摆幅为(4.2/58.5)×425.25=30.5 mm。得到的结果与表1中GPS测量的点位偏差基本一致。

4.2 测量机器人法检核

如图6所示，利用TCA2003测量机器人24 h跟踪布设在塔体上的目标棱镜，实时测定楼体倾斜偏差值[2，3]。考虑仰角因素，选择通视条件较好，且距离适中的基准点架设测量机器人，通过分析，君悦酒店与主塔楼的仰角在41.99°之下，适合架设测量机器人，白天每隔 30 min、夜间每隔 60 min跟踪测量布设在主塔楼上的相邻转换层的监测点。

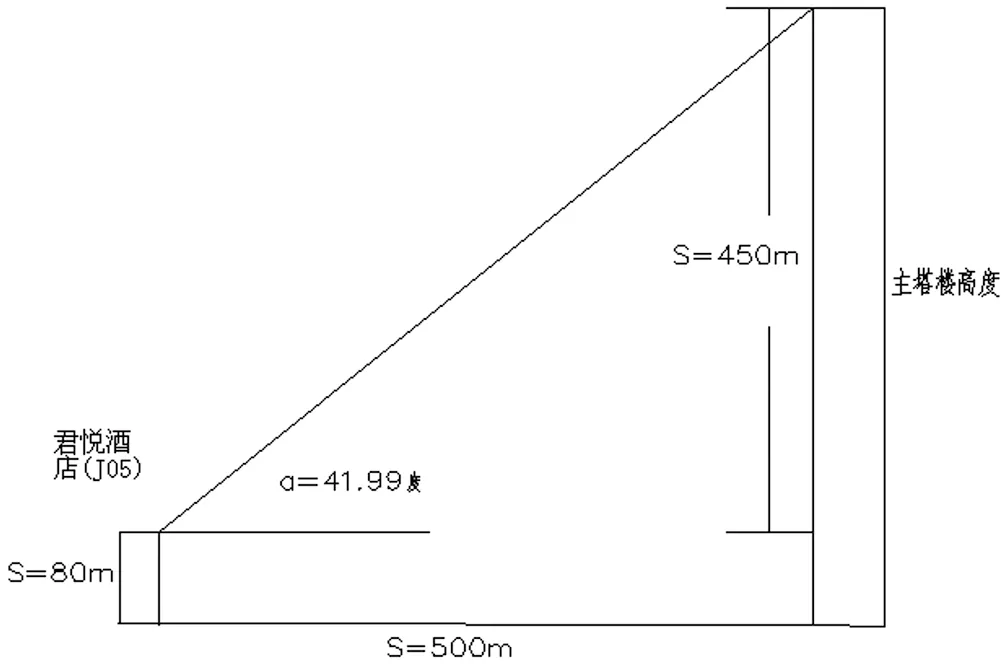
图6 君悦酒店与主塔楼角度分析示意图

同时，在周边大厦设定固定监测站，作为机器人测量精度的检核。测量时，实时测定气温和气压，进行实时改正。观测结果如表2所示：

以103层观测结果为例，其X、Y方向24小时变化规律如图7所示：

从标准偏差看，各监测层变化均在 1 mm～3 mm之间，说明楼体结构稳定、摆动较小；从点位绝对变化值看，最大变化值在 9 mm～13 mm之间，其中夜晚变化量要略小于白天，这与数字正垂分析仪法监测结果相似。数字正垂法85层相对70层，X方向摆动为 3.4 mm，Y方向摆动为 3.4 mm；测量机器人法85层相对69层：X方向摆动为 6.0 mm，Y方向摆动为 6.0 mm。考虑到数字正垂测的是不同楼层之间的相对摆动，测量机器人测的是所测楼层相对地面的绝对摆动，且数字正垂所测结果为 15 min内“楼体平均位置”，测量机器人所测结果为“楼体瞬时位置”，两种方法得到的摆动趋势基本吻合。

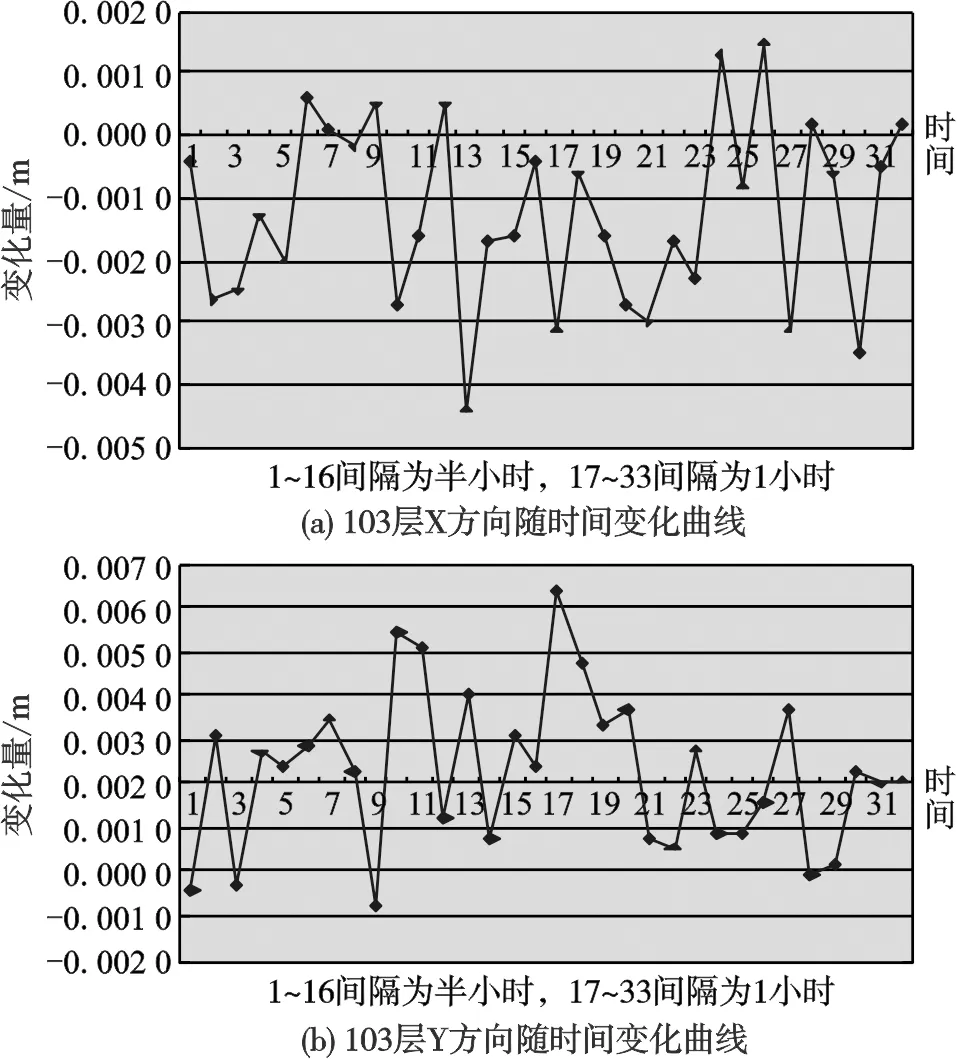
图7 103层X、Y方向随时间变化曲线

5 结 论

本文探讨了基于数字正垂仪获取超高层建筑塔体日周期摆动规律的动态监测方法，为投点改正提供数学模型，有效避免了超高层建筑对施工监测环境的严格要求，实现了全天候的有效投点监测和自动化监测，并实时将观测数据传送至计算机软件，在快速、高精的数据采集阶段的同时，对超高层建筑的日周期摆动轨迹实时处理表达。同时，通过本文的测试可以得到，楼层越高，楼层间相对摆动越大，越应考虑楼体摆动对激光投点的影响；在风力较小的夜晚进行控制网转换、施工投点，能有效避免风力、日照等因素对投点的影响。此外，本文还验证了超高层建筑 50 m～60 m的控制网转换间隔是实用、合理的，对同类超高层建筑监测、施工测量具有指导意义。