基于改进蚁群算法的无人机航迹规划仿真研究

黄心，向煜

(1.重庆数字城市科技有限公司，重庆 400020； 2.重庆市地理信息云服务企业工程技术研究中心，重庆 400020)

1 引 言

无人机具有快速、灵活、机动、高效率的特性，在低空摄影测量中发挥着重要的作用。目前，由无人机得到的航拍图可以应用于城市变形监测、农村地籍测量、三维重建等方面，无人机的广泛使用带来便利的同时，坠落的事件也在不断地发生。在地形起伏较大时，传统的飞行方式往往是通过盘旋上升，使飞行高度高于目标测区的最大高程，这样的飞行方式存在着航线过长且易坠落的概率。目前，在民用无人机方面很少有航迹搜索文献，其多在军用上。

目前对于路径搜索有多种不同的方法，传统的有人工势场法、禁忌搜索法、蚁群算法等[1，2，3]。人工势场法规划的航迹往往是局部最优而非全局最优，禁忌搜索法太过依赖初始解，较差的初始解往往会影响算法的收敛速度，由于蚁群算法有良好的全局优化能力[4，5]，通过引导因子可以改善陷入局部最优的情况。本文从这个方面出发，首先对空间进行划分，通过DEM构建地表模型，判断在所划分的空间上处于地表内部的区域为不可进入以及当前节点到地表距离的倒数作为启发因子，其次利用具有引导因子的蚁群算法实现了自动寻找起飞点和目标测区点的最优航迹路线，生成的航迹自动避开地形，最后通过B样条曲线对航迹进行平滑处理，使航迹真实、可飞，满足无人机性能约束条件。

2 基于改进蚁群算法的无人机航迹规划方法

无人机航迹规划主要包括空间划分、构建启发因子、航迹搜索、航迹平滑4个阶段，如图1所示。

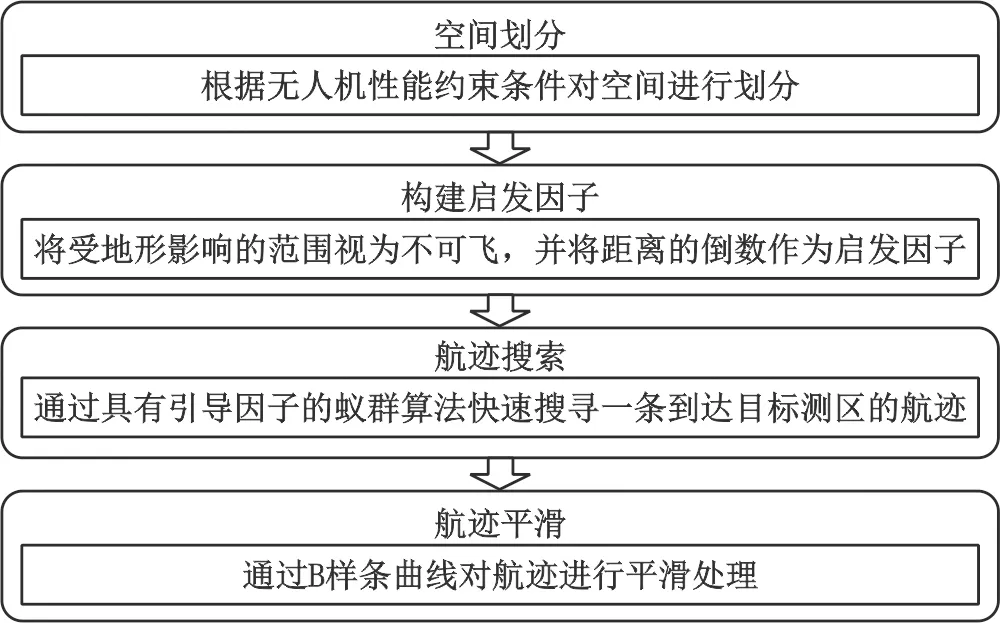
图1 无人机航迹规划技术流程图

2.1 空间划分

在对无人机进行航迹规划前，首先需要根据无人机的性能约束条件来进行空间划分。无人机的性能约束条件包括最小步长、最大爬升角[6～8]。无人机的最小步长是指改变当前飞行状态需要直飞的距离；最大爬升角是指无人机向上攀爬的最大角度。无人机的最小步长和最大爬升角影响的是单元网格的大小。如图2所示，在一个二维平面下，每个节点与节点之间的距离需要大于无人机的最小步长。如图3所示，在三维空间下节点与节点之间的爬升角需要小于无人机最大爬升角，即α≤αmax。

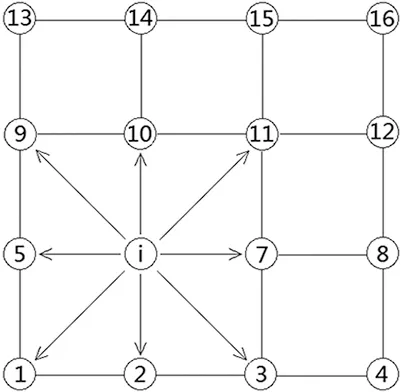
图2 二维空间划分

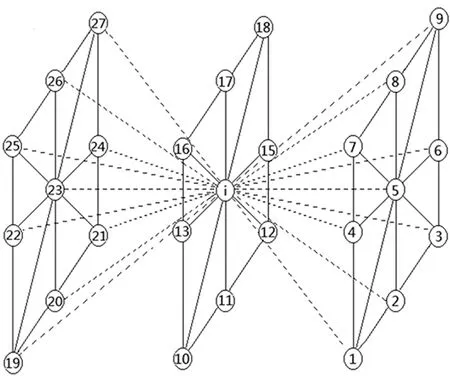
图3 三维空间划分

在三维空间下，通过栅格划分的方式将空间划分为n层二维空间，网格的单元长度分别为XGrid、YGrid、ZGrid，每个节点有26个相邻的节点，通过构建禁忌表删除已经走过的节点，在第一层二维空间上，节点的编号从1开始，直至最后一个节点m，在第二层二维空间上，第一个节点的编号为m+1，依次类推，那么此时节点pi的编号为[9]：

(1)

2.2 构建启发因子

目前地形的表达方式多用数学模型来表示，但是这样表达的方式与实际地形有较大的出入，不能反映真实的情况。本文通过DEM构建地形威胁约束模型，如图4所示3列矩阵分别表示地形约束模型的X、Y、Z值。对地形表面进行网格划分后还需要再将地形表面划分为空间网格大小，如图5所示，通过将地形坐标(X，Y，Z)归到相应空间节点(xj，yj，zj)，通过空间节点高度(xi，yi，zi)和地形归到相应节点高度来判断节点是否满足无人机飞行，当空间节点高度低于地形表面高度，那么此节点视为不可选择，满足此类判断条件的节点也视为地形威胁约束点。

图4 地形威胁约束模型

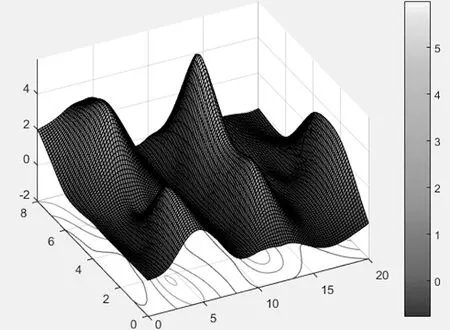
图5 网格划分后的地形威胁约束模型

无人机在飞行过程中与地形威胁约束模型满足以下条件：

(2)

Pi表示节点的启发因子大小，di表示节点i到地形威胁约束模型的距离，Cmax为一个安全值。启发因子的大小与距离有关系，距离越小，威胁越大，反之，距离越远，威胁越小。当节点在影响范围内时，即zj>zi视为不可选，在影响范围外时，视为可选。这样的划分方法可以提高无人机在地形表面的能见度，也可以防止规划后的航迹直接穿越地形。

2.3 航迹搜索

上一节通过对地形和大气的建模，构建启发因子，使无人机避开威胁约束模型；在航迹搜索中传统的蚁群算法是通过信息素浓度来给蚁群正反馈，信息素浓度高的最短路径很快就会被发现，但是在大范围或则复杂地形中，传统的蚁群算法很容易陷入局部最优解，本文利用一种多尺度路径搜索的思路对引导因子进行改进，如图6所示，提高了算法对最优航迹的能见度，使算法能够更快的到达目标点。在状态转移策略中加入信息素、引导因子、启发因子，提高了算法寻找全局最优航迹的能力。

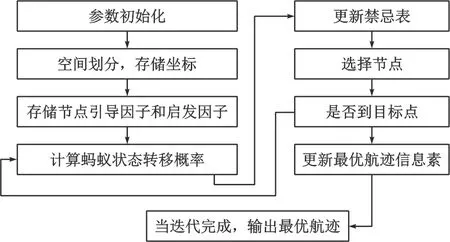
图6 航迹搜索流程图

(1)改进后的引导因子

多尺度路径搜索的思路是连接起点和目标点，当连接线穿过障碍物时，通过作中垂线的方式重新生成一条新的航迹来绕开障碍物，改进后的引导因子见式(3)所示：

(3)

式(3)中，djB表示节点i到起点B的距离，djC表示节点i到目标点C的距离，a、b分别表示权重影响大小。式(3)表示节点选择的概率多在起点与目标连线附近的节点，并且越靠近目标节点引导因子越大，因此航迹规划后的节点分布在直线上或者直线两端。

(2)状态转移策略

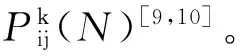
(4)

α表示信息素的重要程度，α为一个常数；β表示启发因子的重要程度，β为一个常数；γ表示导引因子重要性程度，γ是一个常数。Allowedk表示当前还未走过的相邻节点，随着蚂蚁不断选择新的节点，Allowedk也在不断地更新。仿真实验表明：α、β、γ的取值决定了算法的运算速度和效果，取值太小容易使算法不能找到航迹，取值太大易使算法陷入局部最优，而得不到全局最优解。

(3)信息素更新策略

算法每迭代一次，信息素挥发一次也会增强一次，信息素挥发根据式(5)决定，信息素增加根据式(6)决定，信息素增强的策略为每次迭代的最优航迹[11]。

(5)

(6)

Q表示信息素增加强度系数，Q根据仿真实验确定其取值，当算法的迭代次数达到预设最大迭代次数或当前问题求解没有变化或变化不明显时，算法便停止运算。

2.4 航迹平滑

通过蚁群算法搜索的航迹如果只是一条直线段，那么就不需要对航迹进行平滑处理，但是在无人机飞行过程中不可能存在这样一条理想的航迹，因此需要对航迹进行平滑处理，航迹的平滑处理需要考虑无人机的最小转弯半径以及最大爬升角。B样条曲线是贝兹曲线的一种一般化，它具有局部性、几何不变性等性质，当某一控制顶点发生改变时，只会对相邻曲线段产生影响，其他曲线段不会发生改变；当无人机的航迹节点发生变化时，若控制顶点没有改变，其平滑后的航迹也不会改变，因此B样条曲线适合对航迹进行平滑处理[12]。如图7所示，B样条曲线随机对一条折线段进行平滑处理，其拟合的效果较好。P次B样条曲线定义为：

(7)

式中：Pi是控制顶点，Ni，p(u)是p次基函数，它定义在节点矢量U上，并在区间[ui，ui+p+1]上非零。

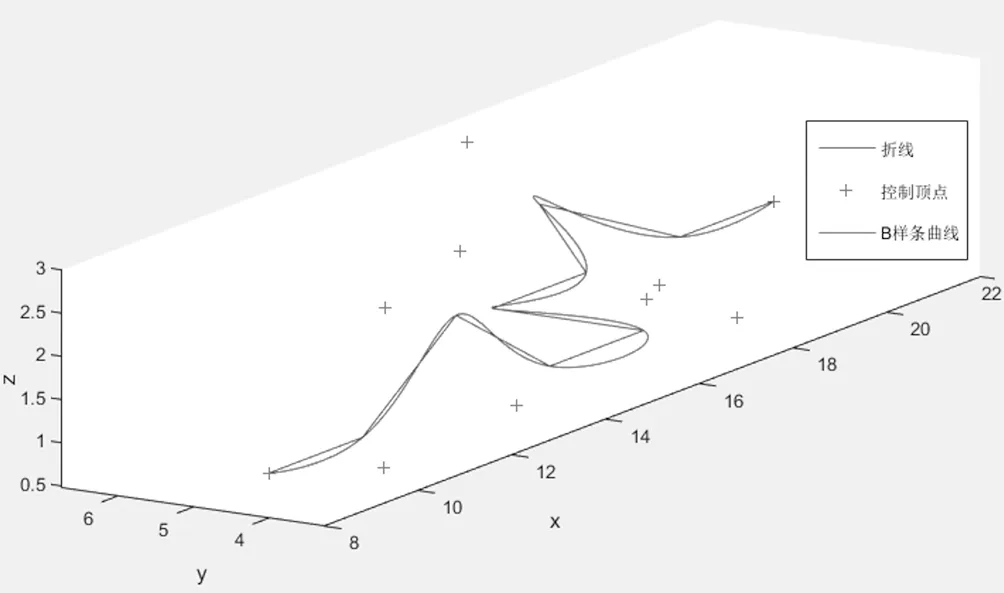
图7 B样条曲线效果图

平滑后的航迹是否可实际飞行，还需要求解出曲线在水平面上的曲率以及在竖直方向的斜率，对P次B样条曲线的定义公式进行形式化求导，可得一阶导曲线，其公式为：

(8)

(9)

将式(7)视为Ci(u)，可见式(8)的形式与B样条曲线的定义公式完全一致。可以直接将Ci(u)看作降阶处理后的(p-1)次B样条曲线，其对应的曲线参数分别为控制顶点Qi、节点矢量Ui。参数ui对应的曲率值k则可表示为：

(10)

参数ui对应的斜率值d可以表示为：

(11)

3 实验成果与分析

以某机型无人机飞行参数为例，其巡航速度为 76 km/h，可飞行时间为 150 min，不考虑飞机坠落情况下有效飞行时间为 125 min，XGrid、YGrid、ZGrid分别为 5 km、5 km、2 km，航迹效果如图8所示：

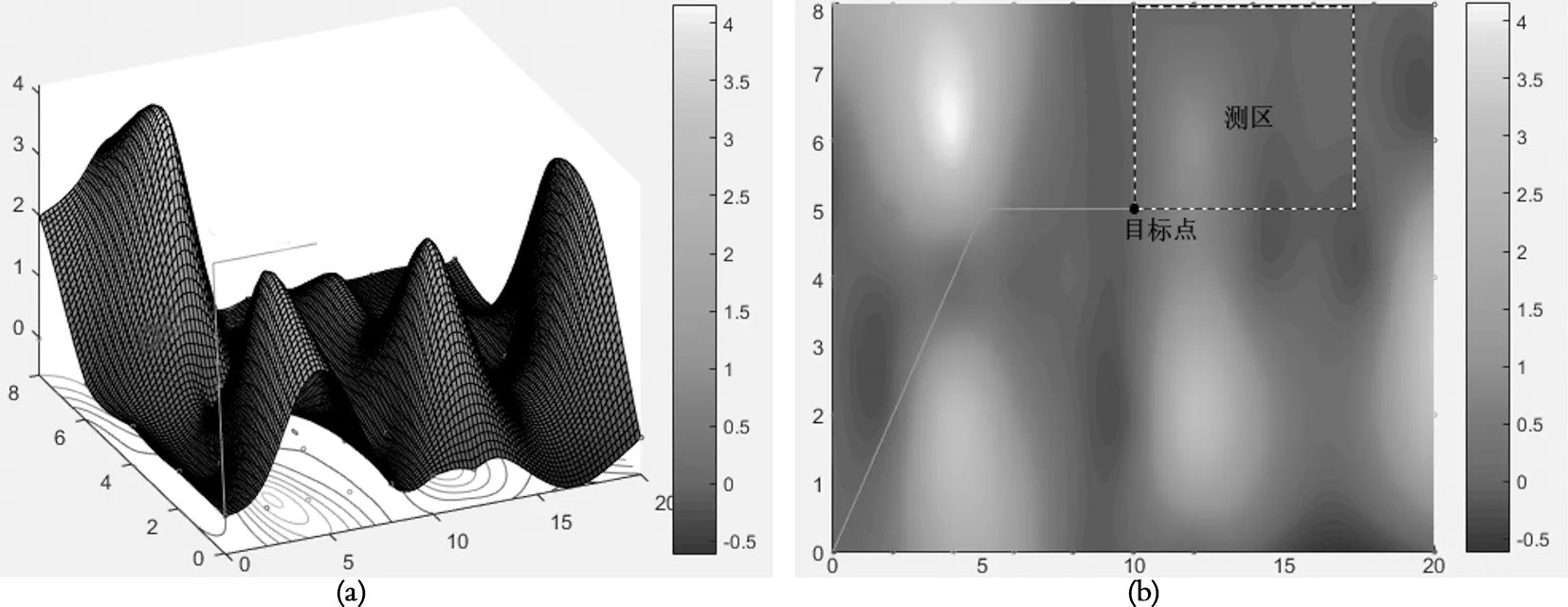
图8航迹搜索效果图

以45°爬升角作为对比，无人机的转弯半径约为 50 m，传统航迹的长度为 15.180 3 km，结果表明，通过改进蚁群算法规划出来的航迹长度为 12.348 5 km，为了计算简便，用航迹长度与巡航速度即可求出无人机飞行时间约为 9.7 min，和手动规划航迹相比较，节约了相对较多的无效飞行时间，规划后的航迹也可以避开已知的威胁，蚁群算法的相关参数如表1所示：

蚁群算法相关参数及算法运行时间 表1

以图8(a)为例，航迹节点为[0，0，0]、[5，5，2]、[10，5，2]，因此B样条曲线的控制顶点仅为3个，因此平滑后的航迹长度有明显增加。如图9(b)所示，当XGrid、YGrid、ZGrid分别为 2.5 km、2.5 km、2 km时，不平滑的航迹长度为 12.097 6 km，随着航迹节点的增加，平滑后的效果也更加理想。由图9可知，合适的网格划分不仅可以增加航迹的精度，也在某种程度上提高了算法的计算效率，随着节点的增加，平滑后的航迹更加逼近原航迹，航迹的长度并没有较大的增加，也没有穿过地形威胁约束模型和其他威胁约束模型。

以无人机的转弯半径为50 m，曲率为20，最大爬升角45°，当XGrid、YGrid、ZGrid分别为 5 km、5 km、2 km，平滑后的航迹曲率及斜率如图9所示：

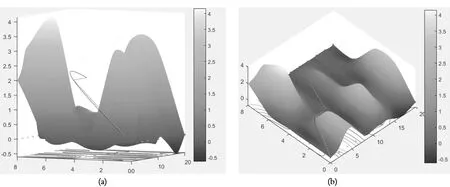
图9航迹平滑效果图

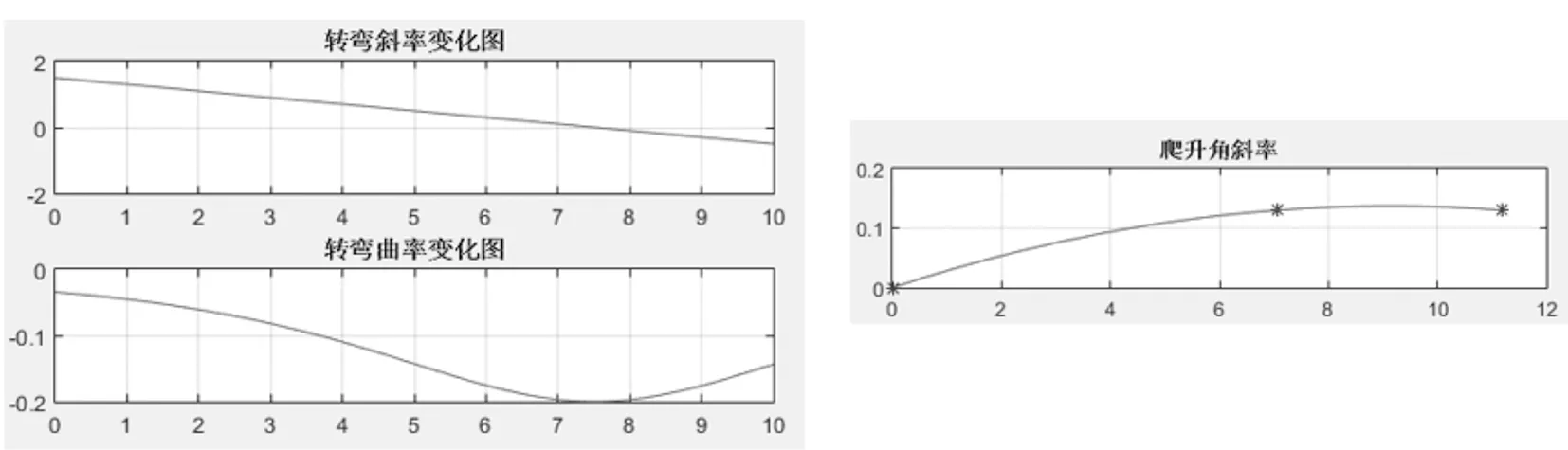
图10 转弯斜率、曲率以及爬升角示意图

由图10可知，平滑后的航迹满足无人机的性能约束条件，因此平滑后的航迹满足无人机的飞行。若无人机的爬升角为30°或15°时，在进行空间划分时适当地调整单元网格的大小使之满足无人机的性能约束条件。

4 结论与展望

通过蚁群算法进行的无人机航迹规划仿真表明，智能规划后的航迹和人工规划的航迹相比，在航迹长度和航迹安全度都有较大的优势，对于威胁约束模型的建模使得无人机飞行更为安全，平滑后的航迹使无人机可以满足其自身的物理性能约束条件，使规划后的航迹真实可飞。本文研究内容对于无人机在进行低空摄影测量时的航迹规划有一定的研究意义。