基于连续-非连续单元方法的露天矿三维台阶爆破全过程数值模拟

冯 春，李世海，郑炳旭，崔晓荣，贾建军

(1.中国科学院力学研究所流固耦合系统力学重点实验室，北京 100190；2.广东宏大爆破股份有限公司，广东 广州 510623；3.鞍钢矿业爆破有限公司，辽宁 鞍山 114046)

爆破开采是露天矿采选总成本控制的首要环节，穿孔爆破的成本较低，仅占整个采选总成本的1/15左右；但是，爆破效果的好坏将直接影响到铲装、运输、破碎等工序的生产效率及能耗。因此，爆破阶段通过改变爆破参数，增大矿岩的损伤破碎程度，减少大块、根底、岩墙等不利因素，将有助于提升后续工序的生产效率。

数值模拟是进行露天矿爆破开采优化设计及爆破效果分析的有效手段。目前，真正可用于爆破破岩全过程模拟的软件主要包括MBM(mechanistic blasting model)软件[1-3]、DMC(distinct motion code)软件[4-8]以及Blo_Up(blast layout optimization using PFC3D)软件[9-11]。MBM及DMC均来自澳大利亚奥瑞凯(Orica)公司，其中MBM是有限元与块体离散元相结合的2D爆破效果数值模拟软件， DMC是基于颗粒离散元的2D/3D爆破效果数值模拟软件。Blo_Up是HSBM(hybrid stress blast model)项目研究成果的集中体现，由ITASCA公司负责产品研发，并由昆士兰大学负责软件模拟结果的验证。Blo_Up采用非理想爆轰模型描述炸药的爆轰过程，采用裂隙流动模型描述爆生气体的楔入破岩过程，采用格子模型描述破碎岩块的碰撞、飞散及堆积过程。

由于MBM、DMC及Blo_Up等露天矿爆破全过程数值模拟软件并未公开发售，因此，对于爆破破岩问题的数值模拟，还是主要借助一些商业软件或一些科研人员自己编制的科研代码，如ANSYS/LS-DYNA、AUTODYN、UDEC/3DEC、FEM-DEM、DDA、CDEM等。丁希平[12]采用LS-DYNA软件模拟了炸药单耗及填塞长度对爆破效果的影响；璩世杰等[13]利用LS-DYNA详细探讨了节理角度对预裂爆破成缝效果的影响规律；Hu等[14]在LS-DYNA中实现了SPH(smoothed particle hydrodynamics)与FEM(finite element method)的耦合计算，开展了预裂爆破及台阶爆破中岩体损伤破裂过程的模拟。谢冰等[15]采用AUTODYN 2D与UDEC(universal distinct element code)相结合的方法，探讨了节理组与炮孔连线的夹角对预裂爆破效果的影响；周旺潇等[16]探讨了利用3DEC(three-dimensional discrete element code)模拟爆破破岩过程的可行性，提出了考虑爆破块度的3DEC块体人工离散方法。Yan等[17]利用3DEC软件，通过在炮孔破碎圈外侧施加等效的爆破载荷，并通过控制不同区域的网格尺寸，研究了三维条件下爆堆的形成过程。Trivino等[18]通过FEM(finite element method)-DEM(discrete element method)方法及跨孔声波测试法研究了爆炸应力波及爆生气体联合作用下岩体中的裂纹扩展过程。甯尤军等[19]通过在DDA(discontinuous deformation analysis)中引入爆生气体膨胀模型，实现了岩石爆破过程中炮孔扩张、岩体破坏、块体抛掷和爆堆形成过程的模拟。郑炳旭等[20]利用CDEM(continuum-based discrete element method)软件探讨了炸药单耗对爆破块度分布曲线及系统破裂度的影响规律。

总体而言，学者们对二维情况下岩石的爆破破碎、飞散及堆积过程已进行了深入研究，但三维情况下的研究依然较少。为此，本文中以CDEM方法为基础，通过引入爆破破岩相关的算法及模型，开展工程尺度下露天矿三维爆破全过程的数值模拟。

1 数值方法及力学模型

1.1 连续-非连续单元方法概述

连续-非连续单元方法(continuum discontinuum element method，CDEM)[21-22]是一种有限元与离散元相互耦合的显式动力学数值分析方法。CDEM的理论基础是拉格朗日方程，为：

(1)

式中：ui、vi为广义坐标，L为拉格朗日系统的能量，Qi为非保守力所做的功。

为了表征多裂纹的萌生、扩展及交汇贯通过程，在CDEM中引入了虚拟裂缝的概念。虚拟裂缝位于每个有限元单元的边界上，在断裂发生之前，通过引入法向罚弹簧及切向罚弹簧可连接两侧的实体单元，并进行力学信息的传递；通过在罚弹簧上设置断裂准则及对应的强度参数，可在虚拟界面上实现拉伸断裂过程及剪切断裂过程；断裂发生后，虚拟界面即转化为真实的接触界面，通过赋予相应的接触模型及接触参数，即可对接触面的力学行为进行准确刻画。

CDEM中的核心控制方程为：

(2)

CDEM采用基于增量方式的显式欧拉前差法进行问题的求解，整个计算过程中通过不平衡率表征系统受力的平衡程度。求解控制方程(2)，共分为3个步骤：第1步循环每个有限元单元，计算单元的变形力及阻尼力；第2步循环每个接触面，计算接触面上的连接力及阻尼力；第3步循环所有节点，计算每个节点的合外力、加速度、速度及位移。

1.2 爆源模型

本文的爆源模型主要采用朗道爆炸模型，该模型的输入参数包括装药密度，炸药爆速、爆热及点火点位置。该模型主要基于朗道-斯坦纽科维奇公式(γ率方程)，为：

(3)

式中：γ= 3，γ1= 4/3，p、V分别为高压气球的瞬态压力和体积，p0、V0分别为高压气球初始时刻的压力和药包的体积，pk、Vk分别为高压气球在两段绝热过程边界上的压力和体积。pk的表达式为：

(4)

式中：Qw为单位质量炸药爆热(J/kg)，ρw为装药密度(kg/m3)。p0的表达式为：

(5)

式中：D为爆轰速度(m/s)。

本文采用到时起爆的方式模拟点火过程及爆轰波在炸药内的传播过程。设某一炸药单元的重心到点火点的距离为d，炸药的爆速为D，则点火时间t1=d/D。当爆炸时间t>t1时，根据式(3)对该单元进行爆炸压力的计算。

钻孔爆破过程中，随着炮孔的起爆，爆生气体逐渐膨胀，并推动岩体做功。岩体在爆炸压力的作用下逐渐出现裂缝的萌生、扩展，并最终出现贯通自由面的裂缝。一旦出现贯通性的裂缝，炮孔内的气体将会从裂缝中快速溢出，并导致炮孔内的压力急剧下降。由于直接模拟爆生气体在岩体内的流动及溢出过程较为复杂，本文中采用设置炸药作用时间的方式进行等效模拟。当某炸药单元起爆后经历的时间大于炸药作用时间时，该炸药单元随即失效，失效后炸药单元中的气体压力为零，且不再进行爆炸压力的计算。

1.3 岩体本构

本文中采用的岩体本构为弹性-损伤-断裂本构，其中在每个有限元单元上施加线弹性本构，输入的参数包括密度及弹性参数(弹性模量、泊松比)；在虚拟界面上施加损伤-断裂本构，输入的参数包括法向连接刚度、切向连接刚度、黏聚力、内摩擦角、抗拉强度、剪切断裂能及拉伸断裂能。

利用增量法表述的单元线弹性本构为：

(6)

式中：σij为应力张量，Δσij为增量应力张量，Δεij为增量应变张量，Δθ为体应变增量，K为体积模量，G为剪切模量，δij为Kronecker记号，t1为下一时步，t0为当前时步。

虚拟界面上采用考虑断裂能的拉剪复合本构进行损伤断裂的计算。首先采用增量法计算虚拟界面处下一时步的法向及切向试探接触力，为：

(7)

式中：Fn、Fs为罚弹簧上法向及切向的连接力，kn、ks为单位面积上法向、切向连接刚度(Pa/m)，Ac为虚拟界面的面积，Δdun、Δdus为法向、切向相对位移增量。

采用式(8)进行拉伸断裂的判断、法向连接力及拉伸强度的修正,如果:

-Fn(t1)≥σt(t0)Ac

那么：

(8)

式中：σt0、σt(t0)及σt(t1)为初始时刻、本时刻及下一时刻虚拟界面上的拉伸强度，Δun为当前时刻虚拟界面上的法向相对位移，Gft为拉伸断裂能(Pa·m)。

采用式(9)进行剪切断裂的判断、切向连接力及黏聚力的修正，如果:

Fs(t1)≥Fn(t1)tanφ+c(t0)Ac

那么：

(9)

式中:φ为虚拟界面的内摩擦角，c0、c(t0)及c(t1)为初始时刻、本时刻及下一时刻虚拟界面上的黏聚力，Δus为当前时刻虚拟界面上的切向相对位移，Gfs为剪切断裂能(Pa·m)。

基于式(8)及式(9)，可绘制出虚拟界面上法向及切向的本构曲线，具体如图1所示。

图1 虚拟界面上的本构曲线Fig.1 Constitutive curves at virtual interface

1.4 接触碰撞算法

爆破后，破碎岩块将以一定的初速度向临空面抛掷，进而出现飞散、碰撞、堆积等爆破现象。本文中采用半弹簧-半棱联合接触碰撞模型[23-24]对大量破碎岩块的接触碰撞过程进行快速、精确地模拟。

半弹簧由单元顶点缩进至各棱(二维)或各面(三维)内形成；半棱仅存在于三维情况，由各面面内相邻的两根半弹簧连接而成(见图2)。建立半弹簧时，缩进距离一般取顶点到各棱或各面中心距离的1%～5%(本文中取5%)。由于只有在半弹簧找到目标面、半棱找到目标棱以后，方能形成完整的接触对并计算接触力，因此称之为“半”弹簧及“半”棱(见图3)。

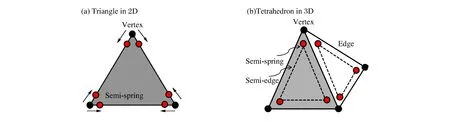
图2 半弹簧-半棱示意图Fig.2 Semi-spring and semi-edge schematics

图3 两类接触对Fig.3 Two types of contact pairs

由于采用了缩进策略，使得半弹簧及半棱均位于面内(二维时位于棱内)，因此半弹簧及半棱均具有各自的特征面积(二维时取单位厚度)，为:

As=Af/Nv,Ae=As,i+As,j

(10)

式中:As及Ae分别为半弹簧及半棱的特征面积，Af为半弹簧及半棱所在母面的面积，Nv为所在母面的顶点个数，As,i及As,j分别为组成半棱的2根半弹簧的面积。

半弹簧-半棱联合接触碰撞模型将二维情况下点-点、点-线、线-线3类接触关系统一为半弹簧-目标棱这一类关系，将三维情况下的点-点、点-线、点-面、线-线、线-面、面-面6类接触关系统一为半弹簧-目标面及半棱-目标棱这2类关系，从而简化了计算，提升了接触检索效率。

一旦接触对创建完毕，即可在接触对上引入传统的接触本构，执行接触力的计算。本文中，当2个块体处于压缩接触状态时执行线弹性计算，当2个块体处于剪切状态时执行库伦摩擦计算；一旦2个块体处于拉伸状态，达到其强度极限时立即断开接触弹簧。

2 单自由面爆破实验的数值验证

以大理岩爆破模型实验[25]作为数值模拟对象。该实验中大理岩块被加工成尺寸为25 cm×25 cm×25 cm的立方体，并在试样一侧钻出直径为0.6 cm、深度为10 cm、间距为5 cm的2个平行钻孔，2个钻孔到岩样顶部自由面的距离均为5 cm(见图4)。采用DDNP炸药进行爆破实验，每孔装药0.3 g。由于试件的尺寸较小，为了减少和消除试件四周自由面对爆破效果的影响，在岩样四周和底部涂上一层黄油，然后用5块1 cm厚的铁板夹制(布孔一侧不用铁板夹制)，并用螺栓固定。

图4 试样及炮孔尺寸Fig.4 The size of specimen and bore hole

数值计算中采用的岩石密度、弹性模量、泊松比、抗拉强度与文献[25]中的一致，分别为2 730 kg/m3、61.4 GPa、0.27、4.72 MPa；岩石黏聚力由文献[25]中给出的单轴抗压强度(90 MPa)及内摩擦角经验值(40°)通过Mohr-Coulomb公式计算获得，为21 MPa；岩石的内摩擦角，拉伸断裂能，剪切断裂能，单位面积法、切向刚度，断裂后滑动摩擦因数等参数文献[25]中未提供，本文中根据相关资料选取了经验值，分别为40°、50 Pa·m、100 Pa·m、2×1014Pa·m、0.25。数值计算中采用的炸药密度、爆速与文献[25]中的一致，分别为1 000 kg/m3、4 950 m/s；炸药的爆热、炸药作用时间等参数文献[25]中未提供，本文中根据相关资料选取了经验值，分别为1.4 MJ/kg、5 ms。

文献[25]中根据耦合及填塞的不同，共开展了3组实验，分别为耦合无填塞、耦合填塞及不耦合填塞(不耦合因数为1.6)，本文中重点对比耦合填塞的实验结果。

建立棱长为25 cm的立方体数值模型，在模型的相应位置设置炮孔，采用15.5万个四面体单元进行剖分。为了模拟实验过程中的铁板夹制作用，将模型底部及四周侧面设置为全约束，模型顶部表面自由。

双孔同时爆破后，不同时刻岩体的破碎情况如图5所示。由图5可得，自由表面处的岩体在爆炸应力波及爆生气体的联合作用下，破裂为若干大块；在内部气体的推动作用下，大块逐渐向外拱出，并发生解体破碎，而爆源附近的大量碎块随之涌出。

图5 不同时刻岩体的破碎运动情况Fig.5 Fracture and movement of rock at different times

爆破7.50 ms后，对脱离母体的碎块进行删除，可获得爆破漏斗的空间形态，如图6所示。对爆破漏斗的形态进行测量，可得A-A′剖面中，爆破漏斗的深度为5.8 cm，爆破漏斗直径为23 cm；B-B′剖面中，爆破漏斗的深度为6.9 cm，爆破漏斗的直径为16 cm。

图6 爆破漏斗的形态Fig.5 Shape of crater

图7 块度分布曲线Fig.7 Block distributing curves

对爆破后各碎块的体积及特征尺寸进行统计，绘制出块度分布曲线对比图(见图7)。其中，文献[25]中的特征尺寸为筛孔直径，数值计算中各碎块的特征尺寸Lc的计算公式为：

(11)

式中：Vb为某碎块的体积，Lmax为该碎块中各顶点间的最大距离。

由图7可得，在对数坐标系下，2条曲线的变化规律基本一致，数值计算给出的块度分布曲线基本呈反“S”型，而实验给出的曲线呈抛物线型。当通过率为40%～50%时，2条曲线对应的特征尺寸基本一致，为33～56 mm；但数值计算获得的特征尺寸在20 mm以下及70 mm以上的碎块比例明显高于实验值。

数值计算及模型实验获得的碎块总体积、K50、K80等指标的对比如表1所示。其中，K50、K80分别为通过率为50%及80%时对应的碎块特征尺寸。由表1可得，数值计算获得的碎块总体积(爆破漏斗体积)及K50与实验值基本一致，误差为16%以下；K80的数值解与实验值差别较大，误差约为52%。

表1 关键指标对比Table 1 Comparison of key indexes

3 露天铁矿台阶爆破模拟

以鞍千露天铁矿的台阶边坡几何尺寸、岩体性质及孔网参数为基础，建立如图8所示的3排7列(共21个炮孔)三自由面台阶爆破模型。台阶高度为12 m，台阶坡角为90°(直立边坡)，炮孔的间排距及抵抗线均为6.5 m，炮孔直径为25 cm，深度为15 m，堵塞长度为6.5 m。采用逐孔起爆方式，孔底起爆，孔间延时为42 ms，排间延时为65 ms。

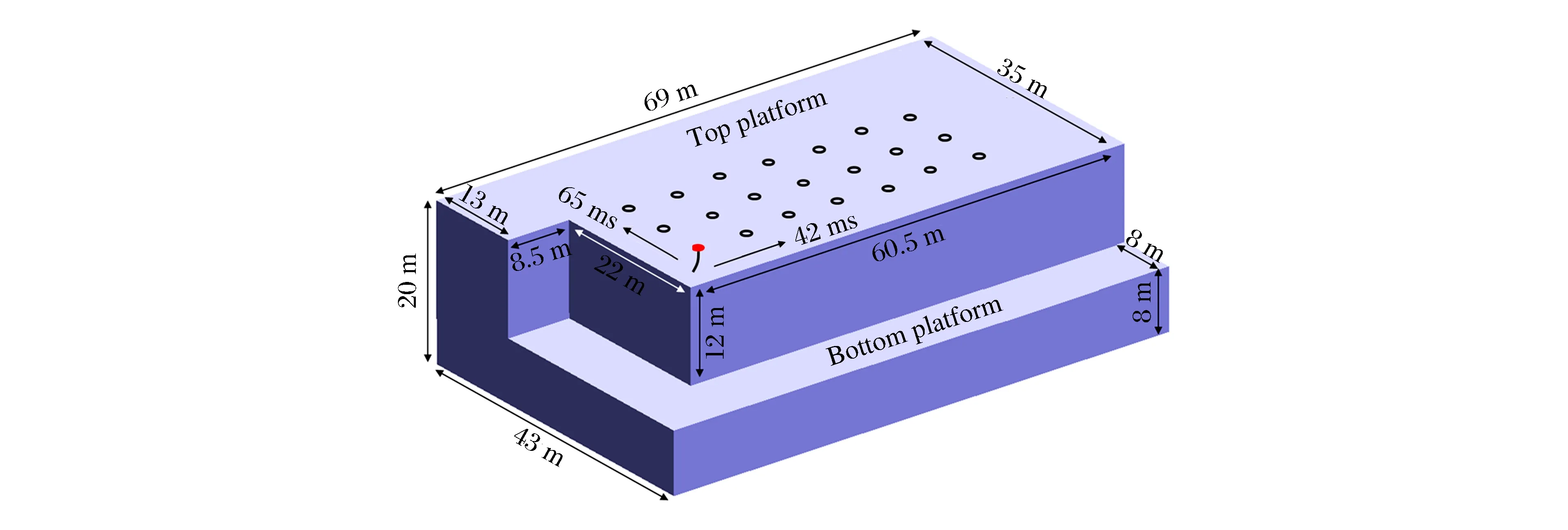
图8 含21炮孔的三自由面台阶爆破模型Fig.8 The bench blasting model with three free surfaces and twenty-one bore holes

对铁矿石块体采用线弹性模型进行描述，其密度为3 200 kg/m3，弹性模量为60 GPa，泊松比为0.25。综合考虑了块体间界面爆区内既有裂隙的强度，采用考虑强度软化效应的损伤断裂模型进行描述，单位面积上的法向及切向刚度为200 GPa/m，黏聚力为12 MPa，内摩擦角为30°，抗拉强度为4 MPa，剪切断裂能为150 Pa·m，拉伸断裂能为50 Pa·m，断裂后滑动摩擦因数为0.58。

爆破所用的炸药为现场混装的乳化炸药，对其采用朗道爆炸模型进行描述，装药密度为1 150 kg/m3，爆速为5 600 m/s，爆热为3.4 MJ/kg，炸药作用时间为35 ms。

数值计算共分为2个阶段：第1阶段为静力平衡阶段，采用虚拟质量法获得模型在重力作用下的静态应力场，在该阶段，模型的底部及四周为法向约束边界，重力方向竖直向下，局部阻尼系数取0.8；第2阶段为爆破破岩阶段，在模型底部及四周施加无反射边界，计算时步取10 μs，局部阻尼因数取0.03，按照预设的起爆顺序及延时进行点火起爆，获得铁矿石的破碎、抛掷过程及最终的堆积过程。

采用四面体网格对上述模型进行剖分，共剖分网格51.1万。受计算量限制，底部平台未进行延伸，宽度仅为8.0～8.5 m，因此爆破后碎块的运动范围将超出底部平台；为了对超出底部平台的块体提供支撑，特设置与底部平台相同高度的刚性面。

爆堆的演化过程如图9所示。由图9可得，2个侧壁临空面相交的区域首先发生了臌胀及抛掷，抛掷方向与等时线方向基本一致。随后，在2个侧壁临空面上分别出现了“爆花”，台阶边坡的中部明显鼓出。当时间大于4.370 s后，爆堆基本形成。

沿着第2列、第4列及第6列炮孔的中心对爆堆进行剖切，观察不同位置处爆堆的表面及内部形态，如图10所示。整个爆堆基本呈上陡下缓的斜坡状，底部坡角为15°～30°，顶部坡角为40°～50°；原爆区顶部出现了较大范围的隆起，最大高度可达2.6 m。第1排炮孔前侧的破碎块体堆积得较松散，后侧区域的破碎块体堆积得较致密；爆区内的岩体在爆炸载荷作用下破碎明显，被纵横交错的裂缝切割为大量碎块；爆区外侧的岩体破碎较轻微，仅在局部区域出现了沿着径向的拉伸裂缝。

图9 不同时刻的总位移云图Fig.9 Displacement magnitude contours at different times

图10 爆堆剖视图Fig.10 Section views of muckpile

图11 破裂度时程曲线Fig.11 History of fracture degree

定义破裂度为数值计算中发生破裂的虚拟界面面积与总虚拟界面面积的比，则破裂度随时间的变化如图11所示。由图11可得，随着爆炸时间的增长，破裂度迅速增大；当爆炸时间大于0.39 s后(最后一个炮孔的起爆时间为0.382 s)，破裂度的增大趋势迅速变缓；爆破完成后，模型的最终破裂度约为85.4%。

采用UniStrong手持式GPS(亚米级精度)，在鞍千矿开展大量的爆堆形态测试。图12给出了南采区典型台阶爆破后的爆堆形态。由图12可得，除后缘拉裂槽外，数值计算给出的爆后斜坡形态、顶部鼓起等现象与现场的测试结果基本一致，证明利用CDEM开展三维露天台阶爆破全过程模拟可行。

图12 南采区的典型爆堆Fig.12 Typical muckpiles in south region

4 结 论

(1)在连续-非连续单元方法(continuum-discontinuum element method,CDEM)中引入了朗道爆炸模型、岩体弹性-损伤-破裂模型及半弹簧-半棱接触碰撞模型，实现了爆炸作用力的精确计算，岩体损伤破裂过程的准确描述以及爆破碎块群飞散、碰撞、堆积过程的快速分析。

(2)开展了单自由面爆破实验的数值对比分析，给出了双炮孔同时爆破作用下，自由表面处岩体的破裂飞散过程，数值计算给出的爆破漏斗体积及块度分布曲线与文献中的实验结果基本一致。

(3)以鞍千矿南采区典型的铁矿台阶爆破开采为背景，模拟了3排21个炮孔逐孔起爆后，爆区内岩体的损伤破裂过程、破碎块体的飞散过程及爆堆的形成过程，数值计算给出的爆堆形态与现场的测试结果具有一定的相似性。