学生“知道了”，老师怎么办

易丽红

老师们在日常的教学中会遇到这样的情况———刚一板书课题，有学生就在下面嚷嚷：“老师，这个我早就会了。”“我爸爸教我了。”“我课外班老师教的。”遇到这种情况，老师们要么无视学生的回答，按部就班地执行教案；要么简单处理，要求学生认真听课；要么不讲解知识直接进入练习环节。这样的处理都不利于学生对知识的掌握。笔者在教学人教版数学教材六年级下册第91页的“数学思考”（如图所示）时也遇到了这样的情况，采取了不一样的做法，效果还不错。

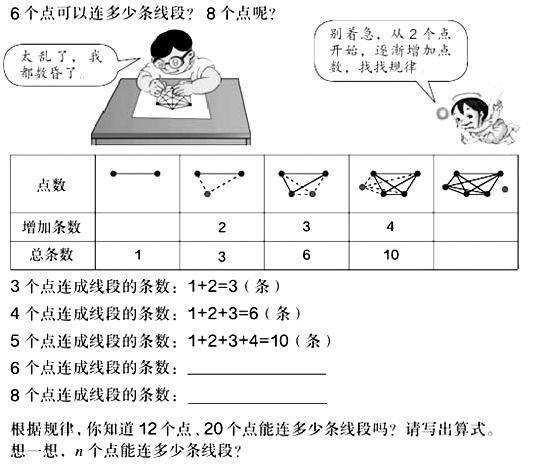
教材编排这道题的目的是让学生学会使用化繁为简的思考方法解决实际问题。课前学情分析时，为了增加思维挑战的难度，我将题目进行了处理，改为直接呈现20个点可以连多少条线段，让学生思考。

题目刚一出示，就有学生说出答案是190条。教师问：“你是怎样想的？”“因为第一个点可以连出19条线段，第二个点可以连出18条线段……第19个点可以连出1条线段，于是19+18+…+2+1=（19+1）×19÷2=190（条）。”教师接着问：“你是怎么知道的？”“我们培训班老师教的。”这时另一个学生说：“我还有另一种解释，就像让20位同学互相握手，每两人握一次，每个人都握19次，这里面有重复计数的，所以是19×20÷2=190（条）。”教师面向全体学生，问道：“你们听懂了吗？”大部分学生都说“听懂了”。这时又有一位学生说：“老师，妈妈教了我这样一种解法：C220=20×19÷2=190。”看来，学生解决这道题没有多少难度，但这节课的教学目标不是教会学生得出问题的答案，而是要让学生体会、理解解决这类问题常用的方法———化繁为简，并能熟练使用这样的方法解决问题。于是教师顺势而为：“既然大家都会了，那么老师出一道题考考大家吧！”学生们信心满满。

教师出示题目：每次上1级台阶或2级台阶，从第1级台阶到第10级台阶，有几种不同的上法？

“10×9÷2=45。”一个学生脱口而出，部分学生也附和。但有学生沉默了一会儿，说：“这道题与刚才的题不同，不是任意两级台阶都可以合在一起。所以不能用刚才的方法。”那怎么办呢？学生一时感到无助。教师提示：“如果只有1级台阶呢？”学生说：“1种上法。”“那2级台阶呢？“”2种。”“老师，我发现规律了。”一个学生兴奋地说，“3级台阶3种上法，4级台阶4种上法……”这时全班沸腾了“：噢，原来这么简单。“”是吗？请同学们写出是哪4种。”学生在本子上写写画画。“不对，应该有5种，分别是（1、1、1、1），（1、1、2），（1、2、1），（2、1、1），（2、2）。”有学生发现了问题。教师启发学生：“看来刚才的发现有问题。我们不妨列一个表格，看看你会有什么发现。”

不一会儿，有学生汇报：“老师，这一回我终于发现规律了：1+2=3，2+3=5，3+5=8……也就是说前面两个结果相加就等于下一个结果。”

教师及时小结：我们刚才是通过什么办法找到规律的？先减少台阶的数量，以便找出结果，然后慢慢增加台阶数，直至发现规律，这种方法就是化繁为简。我们用这种方法再来练习一道题吧。

教师出示题目：每次上1级或2级或3级台阶，从第1级台阶到第10级台阶，有几种不同的上法？

学生开始用学到的方法列表。一段时间后，学生汇报：“老师，我用化繁为简的方法发现，前面3个结果相加就等于下一个结果。”

有學生问：“老师，如果题目是每次上1级或2级或3级或4级台阶，是不是就是前面4个结果相加呢？”教师及时鼓励道：“问得好，我们不是有化繁为简的法宝吗？你可以试一试。你们还愿意接受新的挑战吗？”“愿意！”学生的声音整齐而有力。

教师出示题目：每次上1级或3级台阶，从第1级台阶到第10级台阶，有几种不同的上法？

学生动手列表解答。教师在课堂巡视时，发现有学生列到5个台阶就做不下去了，因为他们觉得无规律可言。教师及时鼓励学生：“没发现就继续列下去，我们不能半途而废，要迎难而上。”

当列到第7个台阶时，有学生发现：“我发现第一项加第三项等于第四项，第二项加第四项等于第五项，也就是隔一项相加。”其他同学在他的启发下也发现了规律，纷纷感叹：“化繁为简太神奇，这么难的题都做出来了。”这时又有学生发现：“前三个连加等于隔一个的结果。”看来一旦找对方法，学生都是潜力无限的。

课的最后，学生都争先恐后谈感受，比以往任何一节课都积极。化繁为简的思考方法已经被他们很好地掌握了，真的要感谢那几个“我知道了”的学生，是他们让课堂如此精彩。这节课的教学也让我有了一些思考。

面对学生“知道了”，教师首先应该了解学情，看学生是真知道还是假知道。所谓真知道，就是学生不仅弄懂了知识的来龙去脉，还能举一反三。所谓假知道，指的是学生课前预习教材时只记下了例题的答案，知其然却不知其所以然；或者是通过其他途径（如课外培训班、家长辅导）确实知道，但大部分学生不懂。

弄清楚了学情，接下来就可以“对症下药”。针对背答案的情形，教师可以这样处理：一是多问为什么。老师装不懂，不断向学生提问，不出几个问题，这位学生就会被问倒。这样学生就明白他还需要认真学习。二是老师将例题进行改编，或修改数据，让学生一时找不到现成的答案，他们就没有机会说“我知道了”。

针对少数学生会，而大部分学生不会的情况，教师可以让已学会的学生充当老师，给其他学生讲解，老师适时补充，这样既锻炼了学生的能力，又能让课堂教学生动活泼。

需要注意的是，无论出现上述哪种情况，老师应当关注的是教学目标是否实现。课例中，学生确实会解此类题，而且能用不同方法解答，但这堂课的教学目标不是得出问题的答案，而是让学生体会、理解解决这类问题常用的方法———化繁为简。因此教学应朝这个目标展开。

教学有法，但无定法，要应对课堂中出现的各种问题，轻松驾驭课堂，教师在课前要做足功课，要比学生站得高、看得远。正所谓“给学生一杯水，自己要有源源不断的活水”。只有这样，师生才能在课堂得到成长。

（作者单位：湘乡市潭市镇明德学校）