“微元法”在高中物理解题中的应用探究

刘姿宇

(湖南省宁乡县第一高级中学 410600)

由于物理习题的解答不仅结合物理知识，还与数学知识和解答方式紧密相关，所以巧妙的借用数学解题能力解答物理试题是应对高考物理难题的重要手段.一般来说，基本的数学知识都会应用到物理解题中，但是在高中物理学习中有关变加速度问题、电磁感应、能量变化等问题的解答，因数学学习中尚未深刻接触高等数学中的积分问题，所以微元法成为解决这类问题的重要解题手段，提升我们在考试和平时练习期间对物理习题解答的正确率和效率.

一、“微元法”的内涵

“微元法”是类似于微积分的一种解题方法，主要利用了微积分的思想，帮助解答高中物理知识中遇到的高等数学积分问题.“微元法”中将研究对象分割为多个十分微小的单元，且这些微小单元遵循相同的物理规律，让变量变为常量，难以确定的量变成易确定的量.一般“微元法”的解题步骤分为：“建立微元研究对象；推广单位到整体；利用“微元法”解题时，将原有的题目分解为相同的微小单位后，对分解出的单元进行过程分析，然后通过物理思想进行解答，进而将题目中要求的问题进行解答.按照物理规律建模解题；取消微元得出结果.“微元法”作为目前较为常用的物理解题方法，能够帮助同学们结合现有物理知识快速解决物理题目，将题目难度简化，提升解题速度.

二、“微元法”在高中物理解题中的应用

1.“微元法”在电磁感应中的应用

高中物理学习中，电磁感应作为重点考察内容，其考试难度和分值占比也具有一定高度.在电磁感应解答中，“微元法”作为常用的一种解题方式，为我们解答这类变量题型做出了巨大贡献.例如：如图1所示，在水平的光滑平行导轨上放置一个质量为m的金属杆，已知导轨间距为L，在导轨一端连接了阻值为R的电阻，其他电阻不计.此时具有垂直导轨的均匀磁场，且磁感应强度为B. 现给金属杆一个水平向右的初速度v0，如果导轨足够长，求金属杆在导轨向右移动的最大距离？

图1 图2

2.“微元法”在运动合成分解中的应用

“微元法”还可以应用到高中物理的变力做功问题中，为解决变力做功问题提供了良好的解题方式.例如，用一个大小不变的力F牵引物体沿半径为R的圆做圆周运动，力F的作用方向始终沿着切线方向，求力F做功的大小？

解：当解答这个问题时不能应用W=FLcosα这个公式，由于该公式智能用于恒力做功，因此，“微元法”在变力做功的题目中更适合使用.在本题目中，F在圆周运动中做的功为正功，且F的运动方向一致.将物体圆周曲线的过程分解为多个微小单元，也就是将圆周分为无数个直线，将变力F做工转换为恒力F做工，然后利用的恒力求解公式W=F·ΔL，接着将所有公式进行加和，即W=ΣFΔL=FΣΔL=F·2πR=2πRF，如此一来就将变力做功转变为恒力做功.

3.“微元法”在变力冲量中的应用

在高中物理的学习中很多问题都是恒力冲量问题为主，但是在我们考核范围内也有变力冲量的问题，那么如何解答变力冲量一直是我们学习的难点.利用“微元法”对变力冲量问题进行解答，有助于这类问题的快速解决，例如：有一段平行导轨分为水平和倾斜两部分(倾角θ= 30°)间距为l，倾斜部分和水平部分的矩形框内各存在垂直平面向上的均匀磁场B1，B2.水平部分的无磁场区域放置了一个质量为3m的“联动双杆”，金属杆cd与ef间用绝缘轻杆连接，长度为L.长度为l、质量为m的金属杆ab从倾斜轨道上端静止下滑，匀速进入水平轨道部分，然后与“联动双杆”相碰后结合成“联动三杆”一起经过水平Ⅱ区域，已知金属杆ab、cd、ef电阻相等为R，一切摩擦不计，平行导轨电阻为零，问“联动三杆”通过虚线框Ⅱ区域产生的热量?如图3.

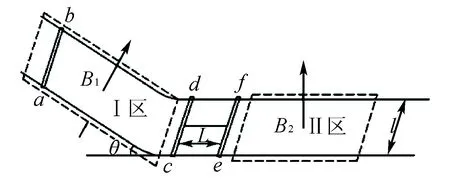
图3

综上所述，“微元法”利用将变化的事物转变为不变的过程帮助我们学生更熟悉物理规律，并快速的解决物理问题，让题目变得简单化，提升了我们的接替效率，降低了题目难度.