一道线性回归方程的变式与应用

■何海虹

同学们在做题时，不要一味地追求题海战术，而应注意典型习题的挖掘，特别是一些优秀的高考题，将它们转化成一些相关的变式题，这样可使大家在试题的变换中，寻求“以不变应万变”的解题方法，从而达到举一反三的目的。

题目根据表1中的样本数据，得到的两个变量y与x之间的回归方程为ˆy=b x+a，则（ ）。

表1

由题意作出散点图，如图1所示，观察图像不难得出，回归方程ˆy=b x+a的斜率b＜0，当x=0时，截距a＞0，所以a＞0，b＜0。故选A。

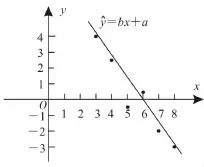
解答此类问题的关键是先画出散点图，再根据散点图中回归方程的斜率、截距来判断系数b，a与0的大小关系。

分析：结合上题中对应的样本数据，通过合适的拓展即可得到如下的一些变式及其应用。

变式1：根据表2中的样本数据，可知两个变量y与x之间的回归方程ˆy=b x+a必过点____。

表2

变式2：根据表3中的样本数据，可知两个变量y与x之间的回归方程可能为（ ）。

表3

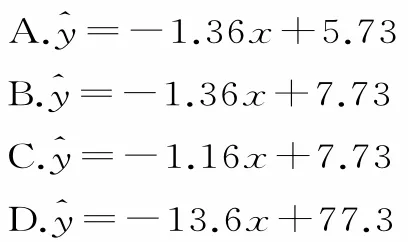
变式3：根据表4中的样本数据，得到两个变量y与x之间的回归方程为ˆy=—1.36x+a，则a的值为____。

表4

变式4：根据表5中的样本数据，得到两个变量y与x之间的回归方程为—1.36x+7.73，则t的值为____。

表5

变式5：根据表6中的样本数据，可知两个变量y与x之间的回归方程中，变量x增加1个单位时（ ）。

表6

先根据题目数据确定对应的回归方程ˆy=b x+a，再结合回归方程中对应参数的性质来确定变量的变化情况，从而得以正确解题。

变式6：根据表7中的样本数据，得到两个变量y与x之间的回归方程为ˆy=b x+a。

表7

（2）试预测当x=10时，对应的y的值。

解答本题的关键是正确求出回归方程，理解回归方程中相应参数的实际意义，并能加以灵活应用。