大孔径厚针孔成像数值模拟研究

姚志明，段宝军，马继明，宋 岩，严维鹏，宋顾周，韩长材

(西北核技术研究所 强脉冲辐射环境模拟与效应国家重点实验室，陕西 西安 710024)

高能X/γ射线或中子具有较强的穿透能力，没有合适的聚焦材料，无法由透镜直接聚焦成像。1969年起，美国洛斯阿拉莫斯实验室开始发展的针孔成像技术[1]是射线源空间分布图像测量的常用手段。针孔成像技术属于直接成像，像与物一一对应，所见即所得。为使针孔成像过程具有较高的空间分辨率，通常将针孔直径设计得较小，典型值为0.5 mm。小孔径限制了针孔对射线的接收效率，无法给出低强度射线源的信息。

相对于针孔成像，编码孔成像技术拥有更大的射线接收角。编码成像是每个物点在接收面上形成1个编码孔投影像，不同物点产生的像相互错开并叠加，物与像不一一对应，需对编码像进行解码复原。目前，适用于高能射线编码的半影孔成像技术在惯性约束聚变的内爆靶丸诊断中得到大量应用[2-4]。半影孔成像将源图像信息编码到半影区域中，孔径大于源尺寸，适用于百μm级尺寸的内爆靶丸诊断。

对于cm级尺寸的射线源，例如FTO(French test object)模型[5]，其内部高原子序数材料在高温流体状态下发生裂变，膨胀过程直径可达10 cm，此时，半影孔孔径需大于10 cm，编码图像接收屏尺寸需达30 cm以上。受测试系统空间布局限制，半影孔成像技术很难应用于大尺寸射线源的诊断。若射线源剂量率低于传统针孔成像系统灵敏度响应下限，就无法给出射线源信息。本文提出介于传统针孔成像和半影孔成像之间的大孔径厚针孔成像方法，基于Geant4蒙特卡罗模拟软件和Matlab图像处理软件建立大孔径厚针孔编码成像和图像复原过程的数值模拟方法，并优化复原算法的输入参数，通过与传统针孔成像结果的比较，评估大孔径厚针孔成像方法的可行性。

1 大孔径厚针孔成像原理

与半影孔成像相似，大孔径厚针孔成像分为两个步骤，如图1所示。第1步是编码成像过程。射线源经过大孔径厚针孔成像，由退化图像记录装置记录为数字化图像。针孔孔径可达mm～cm量级，与传统针孔成像中使用的百μm量级的厚针孔相比[6]，射线接收效率可提高2～4个量级。理想针孔成像的空间分辨由式(1)描述，M为成像系统放大倍数，随着针孔孔径d的增大，空间分辨Δr(物面上可被分辨的两个点源之间的最近距离)线性增加，射线源经大孔径厚针孔后得到的是模糊的像。

图1 大孔径厚针孔成像原理示意图Fig.1 Schematic of large thick aperture imaging

(1)

第2步是图像复原。数字化图像输入计算机后采用算法程序运算解码，得到空间分辨改善后的清晰图像。图像复原过程具有病态性，无法得到与真实图像相同的结果，但可根据针孔点扩散函数(PSF, point spread function)等先验知识，获取尽可能逼近真实图像的近似解。

2 图像复原算法

大孔径厚针孔成像系统物面上不同位置点源的PSF不同，属于空间移变系统[4]。当满足近轴条件时，PSF可认为是空间移不变的，能采用逆滤波、Wiener滤波和Lucy-Richardson等空间移不变图像复原算法复原。退化图像i(x,y)、源图像o(x,y)、针孔PSFh(x,y)和附加噪声n(x,y)之间的关系可由式(2)描述：

i(x,y)=h(x,y)*o(x,y)+n(x,y)

(2)

两边进行Fourier变换，得到频谱形式下的表达式(式(3))，其中，H(u,v)为调制传递函数，I(u,v)、O(u,v)、N(u,v)分别为退化图像、源图像和附加噪声的频谱。

I(u,v)=H(u,v)·O(u,v)+N(u,v)

(3)

2.1 理想逆滤波

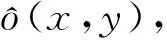
(4)

2.2 Wiener滤波

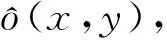
(5)

其中，Sn(u,v)、So(u,v)分别为噪声n(x,y)和真实图像o(x,y)的功率谱，两者的比值为NSR(noise to signal power ratio)。

2.3 Lucy-Richardson算法

Lucy-Richardson算法[8]是1种迭代方法，简称L-R算法。利用贝叶斯公式结合极大似然估计可得到迭代方程，如式(6)所示。其中，k为迭代次数。迭代过程中使用的h(x,y)是在近轴条件下中心轴线位置的PSF。

(6)

2.4 图像复原效果评估

为定量比较不同复原算法的复原效果优劣和寻找迭代复原算法的最优迭代次数，通常引入均方根误差σ[9]，表达式为：

(7)

其中，M和N为图像沿x轴和y轴的像素数。σ越小，图像复原结果在均方根误差意义上越接近源图像，复原效果越好。

3 蒙特卡罗模拟与图像复原

3.1 大孔径厚针孔成像过程模拟

蒙特卡罗方法能逼真地描述射线与物质相互作用的物理过程，Geant4软件包含了p、e-、n和γ射线等多种粒子的物理过程。本文采用Geant4模拟大孔径厚针孔的编码成像过程。射线源为1.25 MeV的γ射线，形状尺寸为6.4 cm×6.4 cm的字母A，射线源距离针孔中心1 m，退化图像记录屏距离针孔中心1 m。计算程序中源粒子发射过程采用偏倚抽样技巧，只在稍大于针孔接收立体角的范围内发射射线，可提高计算效率，缩短计算时间。图像记录过程对射线的能量和种类进行判断，排除次级γ射线和其他射线干扰，只记录直穿γ射线图像。图2a为源图像，图2b～d为退化图像。为便于比较，模拟了孔径为0.5 mm的传统小孔径厚针孔成像，如图2e、f所示。

a——源图像；b——5 mm针孔退化图像；c——10 mm针孔退化图像；d——15 mm针孔退化图像；e——0.5 mm小孔径针孔成像；f——0.5 mm小孔径针孔管道因子校正图像图2 源图像与针孔成像模拟结果Fig.2 Source image and simulation image of aperture

0.5 mm小孔径针孔成像与源图像形状基本一致，由于厚针孔管道因子效应，图像中心区域成像效率较边缘的高，管道因子校正是厚针孔成像的常用方法[6]，管道因子fp随像素与图像中心距离r的变化曲线如图3所示，图2f为校正图像；5 mm针孔退化图像基本保留了字母A的轮廓形状信息，但与0.5 mm孔径针孔成像相比，中心三角形轮廓已变得模糊；10 mm针孔退化图像中几乎无法识别源形状为字母A；15 mm针孔退化图像源形状信息全部损失，仅能观察到模糊的三角形亮斑。随着针孔孔径的增大，成像系统空间分辨率变差，源图像退化严重，结合复原算法恢复源图像信息是必要的。

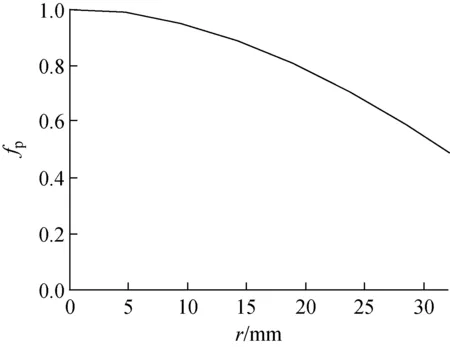
图3 管道因子曲线Fig.3 Curve of fp vs r

3.2 图像复原

Matlab软件中包含丰富的图像处理函数，deconvwnr函数可实现逆滤波和Wiener滤波，输入参数包括退化图像、PSF和NSR。deconvlucy函数可实现L-R复原算法，输入参数包括退化图像、PSF和k。不同孔径针孔轴线的PSF由蒙特卡罗模拟计算得到，如图4所示。

图4 5、10、15 mm孔径针孔PSFFig.4 PSF of 5, 10 and 15 mm apertures

1) 理想逆滤波

采用deconvwnr函数，当NSR设置为0时即为理想逆滤波。复原结果如图5所示。可看出，理想逆滤波算法会引起噪声放大，难以获得清晰的复原图像。

2) Wiener滤波

采用deconvwnr函数，改变输入参数NSR的大小，图像复原解与源图像之间的σ随之变化，如图6所示。针孔孔径越小，σ的极小值越小，图像复原解越接近源图像。针孔孔径越大，σ取极小值时的NSR越小，即真实图像(信号)与噪声的功率谱之比越大。σ取极小值时的复原结果如图7所示，相应的σ列于表1。其中σ0.5为0.5 mm孔径传统针孔成像结果与源图像的均方根误差，为1.03×10-4。Wiener滤波算法可复原得到清晰的字母A的图像，但图像周围存在明显的伪影。随着针孔孔径的增大，伪影现象加重。

图5 理想逆滤波图像复原解Fig.5 Reconstruction result using inverse filtering method

图6 Wiener滤波σ随NSR的变化Fig.6 σ of Wiener filtering vs NSR

图7 Wiener滤波图像复原解Fig.7 Reconstruction result using Wiener filtering method

3) L-R算法

采用deconvlucy函数，改变k的大小，图像复原解与源图像之间的σ随之变化，如图8所示。针孔孔径越小，σ的极小值越小，复原图像越接近源图像。针孔孔径越大，σ为极小值所需的迭代次数越多，迭代收敛速度越慢。σ取极小值时的复原结果如图9所示，相应的σ列于表1。针孔孔径为5、10、15 mm条件下，L-R算法均能复原得到清晰的字母A图像，复原图像中没有明显的伪影。

表1 图像复原解的均方根误差Table 1 σ of reconstruction results

图8 L-R算法σ随迭代次数的变化Fig.8 σ of L-R algorithm vs number of interation

图9 L-R算法图像复原解Fig.9 Reconstruction result using Lucy-Richardson method

3种复原算法相比，理想逆滤波算法会引起噪声放大，难以获得清晰的复原图像。Wiener滤波和L-R算法均可获得清晰的源图像，但Wiener滤波算法伪影现象较严重。与之相比，L-R算法复原图像中无明显伪影，且相同孔径条件下图像复原解的σ极小值更小。因此，L-R算法的图像复原效果最好。

与0.5 mm孔径传统针孔成像相比，结合L-R算法的5、10、15 mm大孔径厚针孔成像获取的图像σ极小值分别为前者的1.15、1.21、1.26倍。说明在均方根误差意义上，大孔径厚针孔成像结果与传统针孔成像接近。图9和图2f直观比较可发现，图9中字母A底部部分细节信息更清晰，初步验证了大孔径厚针孔成像方法具有可行性。

4 结语

为解决cm级尺寸的辐射源空间分布诊断问题，本文提出了介于传统针孔成像和半影孔成像之间的大孔径厚针孔成像方法。采用蒙特卡罗模拟和图像处理软件实现了编码成像过程和图像复原过程的数值模拟。模拟结果表明，大孔径厚针孔成像能获得与传统针孔成像接近的源图像测量结果，初步验证了方法的可行性。

实际测量的脉冲辐射源通常具有能谱复杂、尺寸和射线定向发射强度连续变化的特点，针对具体的测量对象，优化大孔径厚针孔结构，研究更高重建精度的非线性图像复原算法是需要进一步深入研究的问题。