基于综合冲突度量的高冲突证据融合算法
周 莉,孙潇潇,卢林娜,张维华,2
(1.鲁东大学 信息与电气工程学院,山东 烟台 264025; 2.鲁东大学 资产处,山东 烟台 264025)
0 引 言
Dempster-Shafter(D-S)证据理论能够在没有先验知识的条件下较好描述和处理不确定、不完全信息,其融合规则具有随有效证据条数的增加快速收敛的特性,近年来被广泛应用于智能决策、故障分析以及目标识别等诸多应用领域[1-4]。
实际应用中,由于各种客观和人为因素的影响,经常需要处理高冲突信息。此时,由于D-S组合规则采取全局归一化处理冲突信息的做法,其证据合成结果易出现反常现象[5-6]。自该问题被Zadeh于1984年提出以来,许多专家学者对此进行了诸多研究,提出了多种改进措施,主要可归结为3类:①修正证据组合的数学模型或对证据合成规则进行改进[7-8];②对证据源进行预先处理,而后再用D-S组合规则进行证据合成[9-15];③对前述2类做法进行综合,即在对原证据进行冲突度量的基础上,对冲突信息进行合理再分配[16-19]。但无论采取哪一种改进措施,其首要任务均是先要对证据冲突进行准确度量。
针对常用冲突度量参数Jousselme证据距离不能很好处理概率分配值相对分散的冲突证据的冲突度量问题,文献[20]提出改进的Jousselme证据距离函数,改进的冲突度量函数能随证据概率赋值分散程度的增大提高相应冲突度量值,但在证据高冲突情况下,由于改进证据距离函数仍不能很好描述证据之间的局部冲突状况,导致其冲突度量结果仍然偏低。为此,本文考虑将证据非包含度引入上述改进的Jousselme证据距离函数,使新的冲突度量函数能随证据之间非包含度的增大按一定幅度增大,并基于新的综合冲突度量结果对局部冲突信息再分配比例进行进一步调整与改进。理论分析和仿真实验结果表明,本文所提综合冲突度量函数,能够提高对高冲突证据的冲突度量精度,进而在不同程度上提高冲突证据融合结果的可靠性和稳定性。
1 证据理论
1.1 D-S组合规则及其不足

设mj(j=1,2,…,J)是J个相互独立的基本概率赋值函数,其D-S组合规则定义为
(1)
(1)式中,
…mJ(Al)]
(2)
D-S组合规则中的冲突系数k表示证据之间的不一致性,也称为不一致因子。当k=1时,D-S组合规则失效。且研究表明,当k接近于1时,其证据合成结果会出现与实际情况相矛盾的结论。不难看出,这种矛盾结果是由证据之间的冲突造成的,通常证据之间的不一致因子k越接近1时,表明证据体之间的冲突程度越大。当证据体之间含有的一致性信息太少,经典D-S组合规则由于信息缺乏导致证据合成结果出现错误。
1.2 冲突证据的融合
1.2.1 冲突度量
当前,常用的冲突度量参数包括冲突系数、证据距离、信息熵、重合度、相似度以及虚假度等。但单一的冲突度量参数均存在某些方面的不足,无法独立完成对各类冲突证据的有效度量。例如,毕文豪等[11]提出利用证据相似度函数度量证据冲突,在某些情况下能够得到比使用Jousselme证据距离更好的冲突度量效果。但研究发现,该类相似性度量函数与Jousselme证据距离函数一样存在当证据概率赋值较分散时,对证据冲突度量结果不够准确的不足。毛艺帆等[21]提出利用重合度对证据冲突进行度量,在一定范围内能够提高概率赋值较分散证据之间的冲突度量效果。但随着证据之间冲突程度的增大,特别是对含有非单子集焦元的冲突证据,其冲突度量效果仍不够理想。彭颖等[20]通过对Jousselme证据距离进行改进,使冲突度量函数值随待融合证据模值的减少而增大,较好地改善了Jousselme证据距离函数随证据概率赋值分散程度的增大,其冲突度量值偏低的不足,但该改进度量函数在描述高冲突证据时,仍存在冲突度量值偏低的不足,且改进的Jousselme证据距离函数仍属于单参数度量函数,不能够随着冲突程度的增大,对冲突度量值进行调整,算法缺乏灵活性。类似的单参数研究结果还有很多,但均存在一定的不足。因此,分类、多参数组合利用必将成为人们今后对证据进行冲突度量的首选策略。
1.2.2 冲突证据的合成
基于冲突度量获取证据的可信度之后,修正证据源的改进算法通常采用类似文献[9]的算法流程,对待融合J条证据的加权证据体利用D-S组合规则进行自身融合J-1次,得到最终证据合成结果。该类算法的优点是算法具有可结合特性,不足是该类算法证据合成结果的准确性完全取决于对证据的冲突度量结果。而在基于局部冲突信息再分配的一类改进算法中,证据合成结果的准确性不完全由证据可信度的计算结果所确定。也就是说即使证据可信度的计算结果存在一定误差,该类算法仍有望通过对局部冲突信息的合理再分配,对上述冲突度量误差进行修正,从而提高证据合成结果的准确性。
文献[16]基于Jousselme证据距离度量证据冲突,并将冲突度量结果用于对两两证据合成过程中形成的局部二元冲突信息进行再分配,在一定合成顺序下能够提高证据融合精度,但该算法对证据合成运算不具有可结合性,算法稳定性差。而对多元冲突组合所含矛盾信息直接进行按比例再分配的多证据直接合成算法,不仅可以提高多元冲突信息的利用率,且可以避免证据合成顺序对结果的影响,提高证据合成结果的可靠性,但该类算法又存在计算量较大,且算法收敛进度缓慢的不足。
基于上述分析,本文考虑首先对证据冲突度量算法进行改进,并据此对证据融合顺序予以优化;其次进一步对焦元支持度的计算式进行改进,并将改进的证据可信度应用于对焦元可信度的加权归一化处理中,从而强化证据可信度在二元冲突信息再分配中的作用。
2 改进综合冲突度量算法
2.1 已有改进冲突度量算法
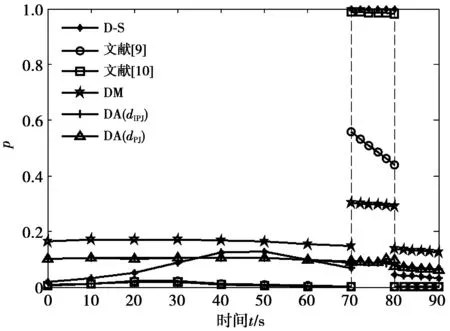
设mi和mj(1≤i (3) (4) (4)式中,|·|为求模运算;Ak,Bl∈ρ(Θ),ρ(Θ)为Θ的幂集。 一般情况下,dJ(mi,mj)的值越大,表明2条证据mi和mj之间的冲突程度越高。在证据之间的冲突程度不是很高时,dJ(mi,mj)能够较好刻画证据mi和mj之间的冲突程度。但当2条证据存在高度冲突时,已有研究表明,此时基于Jousselme证据距离函数对证据冲突进行度量的取值偏小,导致冲突证据在证据融合过程中所占权重偏高,严重影响证据融合效果。为此,文献[20]提出针对高冲突证据进行冲突度量的改进Jousselme证据距离函数dPJ(mi,mj)为 (5) 由于 仔细分析(3)式可以看出,Jousselme证据距离函数不能对概率赋值较分散的冲突证据进行准确冲突度量的原因是该函数缺少对局部冲突信息的描述,文献[20]利用证据模值的大小刻画证据概率赋值的分散程度,但仍没有对不同证据之间的局部冲突情况进行具体刻画,导致(5)式对部分高冲突证据进行冲突度量的结果仍然偏低。 为提高(5)式对高冲突证据冲突度量结果的准确性,本文在(5)式的基础上,提出新的综合冲突度量函数dIPJ(mi,mj)为 dIPJ(mi,mj)= (6) (6)式中:a为可调参数,其取值为[0,20],通常可根据证据间冲突程度的大小,调整a的取值,当a=0时,(6)式退变为(5)式,随着a取值的增大,证据mi和mj之间的冲突度量值相应增大;nc表示证据之间的非包含度,其定义为 (7) (7)式中,Al∈ρ(Θ)。(7)式中等式右端的第2项刻画了证据mi和mj概率赋值之间的重合程度,即证据之间的相互包含度。因而,nc(mi,mj)描述了两证据之间的非包含度大小。 与(5)式相比,(6)式通过引入非包含度刻画不同证据之间的局部冲突程度,并能通过调整参数a的取值更好地度量证据概率赋值较分散情况下的证据冲突程度,有望减小差异证据对证据融合结果的影响,提高冲突证据融合结果的稳定性。 文献[16]针对两两证据融合的局部冲突信息再分配算法进行改进,主要计算步骤如下。 1)根据(3)式计算J条证据中每2条证据mi和mj之间的Jousselme证据距离,得到d(mi,mj),∀i,j=1,2,…,J; 2)计算各证据的支持度及信任度分别为 ,mj)] (8) (9) 3)基于(9)式计算J条证据的加权证据体为 ·mi(Ak), ∀k=1,2,…,n (10) (10)式中,n是证据中焦元的个数。 4)则焦元的信任度及其在冲突分配中所占比例系数分别为 FCrd[mi(Ak)]= (11) i=1,2,…,J;k=1,2,…,n (12) (11)式、(12)式中,AD[mi(Ak)]为mi(Ak)与mMAE(Ak)之间的距离; 5)于是,基于局部冲突信息重新分配的改进D-S组合规则为 m(X)=m∩(X)+ (13) 上述改进算法对形如XY的局部冲突信息进行了重新分配,以期达到提高冲突信息利用率的目的。但仔细分析可以看出,上述改进算法仍存在几点不足:①对于高冲突证据,基于Jousselme证据距离计算所得2条证据之间的冲突度量结果d(mi,mj)取值偏低;②证据及焦元信任度计算式也存在对高冲突证据冲突度量结果偏低的不足;③上述两两证据合成算法不满足结合律,影响证据合成结果的稳定性。 针对已有改进两两证据合成算法存在的不足,提出新改进两两证据融合算法如下。 Step1利用(6)式计算证据mi和mj之间的综合冲突度量dIPJ(mi,mj),并利用(14)式计算得到改进的证据支持度s(mi),进而利用(9)式和(10)式分别计算得到对应的证据可信度c(mi)和加权证据mw(Ak); ,mj)] (14) Step2将J条证据按证据可信度取值c(mi)自小到大进行排序,即得到优化的两两证据融合顺序; Step3为提高各证据中不同焦元支持度的计算准确性,除了考虑mi(Ak)与焦元Ak的中心值mw(Ak)之间的相似程度。在这里还考虑到不同证据中的焦元被其他证据中同一焦元支持的程度,为此,定义证据mi中焦元Ak的支持度为 , ∀i=1,2,…,J;k=1,2,…,n (15) 将(15)式归一化,得 ,∀i=1,2,…,J (16) 定义证据mi中焦元Ak的信任度为 Fc12[mi(Ak)]=Fc1[mi(Ak)]Fc2[mi(Ak)] (17) (17)式中, Fc2[mi(Ak)]= (18) 考虑到证据可信度的重要性,基于证据可信度对证据mi中焦元Ak的信任度进行加权归一化为 ∀i=1,2,…,J;k=1,2,…,n (19) Step4将ω[mi(Ak)]作为二元冲突信息再分配中焦元Ak的分配系数,并依Step2中的证据排序依次对J条证据进行两两融合,得新改进的两两证据融合算法为 在上述算法Step 1中,若利用(6)式计算证据距离时,取参数a=0,对应得到的算法称为新算法(dPJ);若取参数a=8,对应算法称为新算法(dIPJ)。 与文献 [16]算法相比,新改进算法在度量证据冲突时,不仅采用了更适用于度量高冲突证据的综合冲突度量函数进行冲突度量,且将文献[16]算法中的证据支持度计算(8)式替换为更适用于描述高冲突证据偏离程度的(14)式,在较大程度上降低了冲突证据在证据融合中的权重;并在此基础上改进了焦元支持度计算式及焦元冲突分配系数,有望在一定程度上提高对冲突证据的融合精度。 为验证本文所提2种新算法的有效性,以下给出2种新算法与其他相关算法的证据融合结果比较。 例1目标识别框架为Θ={A,B,C},4条证据分别为 m1∶m1(A)=0.00,m1(B)=1.00,m1(C)=0.00; m2∶m2(A)=0.60,m2(B)=0.30,m2(C)=0.10; m3∶m3(A)=0.53,m3(B)=0.35,m3(C)=0.12; m4∶m4(A)=0.51,m4(B)=0.40,m4(C)=0.09。 解利用不同相关算法对上述4条证据进行合成,所得证据融合结果如表1所示。 表1 相关算法的证据融合结果 表1中,加法加权即采用(8)式、(9)式计算只基于Jousselme证据距离的证据支持度和可信度所得加权证据体;而乘法加权是指利用形如(14)式的计算式计算证据支持度所得加权证据体;相应地,直接加法和直接乘法分别指在多证据直接融合算法中采用(8)式和(14)式分别计算证据支持度的对应证据融合结果。 由表1可知,除D-S组合规则和文献[10]算法将目标识别结果确定为B以外,其余算法的目标识别结果均为A。通过对4条证据进行直观分析,也认为正确的目标识别结果应该为A。D-S组合规则错误地将B识别为目标,其原因主要是该问题存在“一票否决”现象。另外,由于该组证据中存在一条高冲突证据,文献[10]算法采用对虚假度和证据余弦距离加权平均的方式计算证据冲突的做法不利于解决对该类证据的冲突度量问题,导致识别结果出错。 文献[9]算法的结果即是对加法加权证据利用D-S组合规则进行自身融合3次所得,其结果通常是朝着加法加权证据的目标识别方向进行一定程度的聚焦,因此,该类算法中,冲突度量结果是否准确显得至关重要。由于该组证据属于高冲突证据,因此在计算证据可信度时,采用形如(14)式计算证据支持度优于使用(8)式,因此,有乘法加权优于加法加权,对应还有直接乘法优于直接加法。其原因是采用形如(14)式的计算结果能够赋给高冲突证据更小的支持度,有利于减少其对证据融合结果的影响。在该例中,证据的自然排序对文献[16]算法相对有利,因此,其目标识别结果相对较好,如果采用文献[16]算法对该例中4条证据进行逆序合成,则其结果为m(A)=0.26,m(B)=0.74,m(C)=0.00。显然,前后目标识别概率差异较大。而新算法由于对证据合成顺序利用改进的证据可信度进行了优化,且对证据及焦元支持度计算式进行了合理的改进,2种新算法的证据融合结果明显高于其他算法的对应结果,其中,与直接乘法算法相比,新算法(dIPJ)的正确目标识别概率提高了0.12个点。与对证据采用预处理算法的文献[20]算法相比,尽管新算法(dPJ)未间接利用聚焦速度较快的经典D-S组合规则进行证据合成,但其正确目标识别仍提高了0.023个点。其原因是新算法(dPJ)不仅利用(14)式替换文献[19]算法中采用的(8)式计算证据支持度,且针对局部冲突信息的再分配权重进行了改进,在不同程度上提高了冲突信息的利用率。且与新算法(dPJ)相比,新算法(dIPJ)的正确目标识别概率也提高了约0.03个点,其主要原因是新算法(dIPJ)所采用的综合冲突度量函数能够在文献[19]所提改进证据距离函数的基础上,根据证据之间非包含度的增大,相应提高其冲突度量取值,减少了差异证据对证据融合结果的影响,从而提高了证据融合精度。 大量的算例实验结果表明,对于冲突程度较高的证据,综合冲突度量函数中的可调参数a取8比较合适,如果继续增大a的取值,对冲突证据的融合效果有一定改善但已不很明显。而对于一般性冲突证据,可根据待融合证据的冲突程度的大小将可调参数a的取值设置在0到3之间。 例2设有7部雷达同时对某区域3个未知目标进行跟踪识别,识别框架Θ={A,B,C},其中A为战斗机,B和C均为普通客机。3个目标A,B,C均在与雷达识别系统相距100 km处相对行驶,3个飞行物的行驶速度均为1 000 m/s。雷达1正确识别所测目标为战机的置信度始终分别为0.6,0.3,0.1,雷达2正确识别所测目标为战机的置信度始终分别为0.01,0.49,0.5。雷达3至7在100 km处对目标A机型正确识别的置信度均为0.25,在10 km处对A机进行正确识判别的可能性大小均为0.7,该期间,其对战斗机的判别准确性大小与其相对间距成反比;在整个观测过程中,除干扰阶段外,雷达3至7正确识别观测目标B为战机的可能性大小始终分别为0.2。 在与目标相距30~20 km处,雷达6和7受到干扰,正确识别A,B机型的可能性大小为0。 图1、图2分别是在以上所述仿真背景下,采用不同算法的证据融合结果。图3和图4是在雷达1对目标探测结果进一步变差情况下相关算法的证据融合结果,具体是雷达1正确识别观测目标为战斗机的置信度始终分别为0.45,0.45,0.1,其余探测条件不变。 图2 B机为战斗机的概率Fig.2 Probability of aircraft B as a fighter 由图1、图2可以看出,在一般仿真环境下的非干扰阶段,文献[9]和文献[10]算法的目标识别概率均较高,且优于直接融合算法以及本文所提2种新算法。其原因是前述2种算法均间接使用了D-S组合规则对加权证据进行合成,该规则的优点就是对于非冲突证据具有较好的融合能力和较快的收敛速度。D-S组合规则的目标识别能力在初始阶段较差,低于其他各种算法,但仍能随着探测环境的逐步变好尽快识别出目标,该结果进一步说明,D-S组合规则不适用于处理冲突证据。在高冲突阶段,D-S组合规则和文献[10]算法均不能正确识别出目标,错误地将B识别为战斗机,而直接融合算法和文献[9]算法尽管能够识别出目标,但其正确目标识别概率已远远低于本文所提2种算法。在干扰阶段,本文所提2种算法的正确目标识别概率相差不大,但新算法(dPJ)的正确目标识别概率随时间增加的增势变化较平缓。由图3、图4可以看出,随着探测环境的进一步恶化,在高冲突阶段,新算法(dIPJ)优于新算法(dPJ)的幅度逐渐增大,与新算法(dPJ)相比,新算法(dIPJ)的正确目标识别概率约高出0.1个点。而此时,文献[9]算法已不能正确识别出目标,直接乘法尽管能够正确识别出目标,但其正确识别概率低于新算法(dIPJ)约0.38个点。由图1、图3可知,本文所提新算法(dIPJ)不仅能够较好融合高冲突证据,对于一般性冲突证据,也具有较好的证据融合效果。 图3 A机为战斗机的概率Fig.3 Probability of aircraft A as a fighter 图4 B机为战斗机的概率Fig.4 Probability of aircraft B as a fighter 本文在对已有证据冲突度量参数进行深入研究的基础上,提出一种适用于对高冲突证据进行冲突度量和证据融合的改进算法。与已有Jousselme证据距离函数和改进Jousselme证据距离函数相比,新的综合冲突度量函数能够随着证据之间非包含度的增大可调节性地增大综合冲突度量值,避免了Jousselme证据距离函数随证据概率分配值分散程度的增大其冲突度量值反而变低的不足,与彭颖所提改进Jousselme证据距离函数相比,新的冲突度量函数具有更好的灵活性和更广泛的适用性。由仿真实验结果图3、图4可以看出,随着探测条件的恶化,本文所提基于综合冲突度量函数的新算法表现出较高的稳定性和较强的抗干扰能力。如何更好地对多种证据冲突度量参数进行组合优化利用,并结合使用适用的证据及焦元可信度计算方式,多方面提高冲突证据的融合精度和稳定性,是下一步需要继续进行深入研究的一项工作。
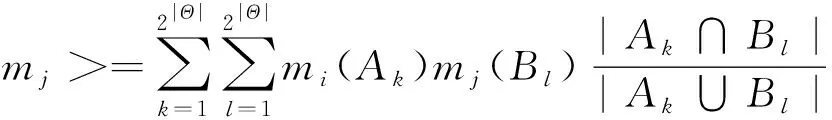

2.2 新改进冲突度量算法
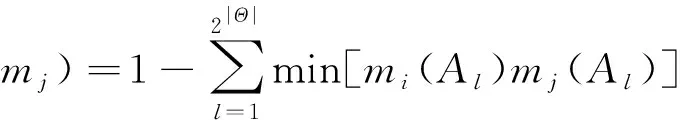
3 改进证据融合算法
3.1 已有改进两两证据合成算法
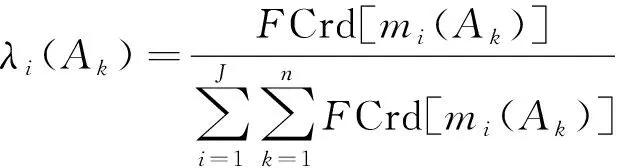
3.2 新改进两两证据融合算法

4 算例与仿真分析



5 结 论

