理想格上支持访问树的属性基加密方案
于金霞,杨超超,杨丽伟,汤永利,闫玺玺
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
0 引 言
属性基加密与传统的公钥加密相比,具有用户的动态性、访问策略的灵活性以及用户身份的隐私性等优点。2005年,Sahai和Waters[1]在欧洲密码学会上提出了属性基加密的概念,它用一系列属性来表示用户的身份,由属性集合和访问结构之间的匹配关系确定其解密能力,并给出一个支持门限结构的属性基加密(attribute-based encryption,ABE)方案。2006年,Goyal等[2]根据加密策略的不同,将ABE体制划分为2类:①密钥策略ABE(key-policy attribute based encryption,KP-ABE),其特点是将访问结构嵌入到密钥中,密文中包含特定属性集;②密文策略ABE(ciphertext-policy attribute based encryption,CP-ABE),它是将访问结构嵌入到密文中,密钥中包含特定属性集,当属性集和访问结构匹配时,即可解密。同时,作者提出支持树形访问策略的KP-ABE方案,和门限访问结构相比较,树形访问结构更为精细,表达能力更为丰富,逻辑操作更具有现实意义。2007年,Bethencourt等[3]提出第一个CP-ABE方案,访问结构采用门限结构。相对于密钥策略属性基加密机制而言,密文策略的属性基加密体制更适用于动态场景,发送者可以设计访问结构,控制接收者的范围。同年,Ostrovshy[4]提出包含非门访问结构的属性基加密方案,更加丰富了访问策略。2011年,Waters[5]利用线性秘密共享方案(linear secret sharing schemes,LSSS)提出了一种新的密文策略属性基加密方案。和树形访问结构相比,LSSS拥有相同的功能,而树形访问结构更为直观,LSSS中秘密分享矩阵设计较复杂。属性基加密机制凭借其访问控制的灵活性等特点成为研究热点,同时,属性基加密机制也被广泛应用,各种相关ABE方案[6-8]相继被提出。但是,上述方案大多是建立在双线性对基础上的,加解密过程中需要多次双线性对运算,存在计算复杂度较高且无法抵抗量子攻击等问题。
基于格的密码体制被认为可以抵抗量子攻击,而且格上多数运算属于线性运算,所以运算效率高。因此,近年来基于格论构造的加密方案受到广泛关注。格上存在许多困难问题,如最短向量问题(shortest vector problem,SVP)等。2012年,Boyen[9]基于标准格上LWE(learning with error)问题,将LSSS应用于格上属性基加密方案中,提出第一个格上KP-ABE方案,满足随机预言模型下安全。同年,Zhang等[10]利用抽样算法提取属性私钥,密文中嵌入门限访问结构,提出第一个基于LWE难题的格上CP-ABE方案。2013 年,Wang[11]提出了标准模型下格上的密文策略的属性基加密方案,该方案实现了多值属性上的门限访问结构,并在 LWE 假设下证明了方案的安全性。相较于标准格上的 LWE 密码体制,基于理想格上R-LWE(learning with error over ring)的方案具有密钥尺寸小、加密效率高的优势。2014年,Zhu等[12]将门限访问策略引入理想格上,提出理想格上基于R-LWE问题的KP-ABE方案,并证明其满足选择明文攻击安全。2015年,Tan等[13]提出基于R-LWE问题的理想格上支持LSSS访问策略的CP-ABE方案。2017年,Chen等[14]指出Zhu等[12]和Tan等[13]的方案安全性证明不能满足选择明文攻击安全。闫玺玺等[15]采用LSSS访问结构提出理想上的多机构CP-ABE方案。同年,Wang等[16]提出有效的基于R-LWE选择密文安全的加密方案。
目前,格上属性基加密方案的研究还不太完善,存在许多待解决的问题。现有的一些方案仅支持单一的访问策略,无法支持灵活的表达方式。本文利用访问树结构和理想格上R-LWE问题提出一种支持任意访问结构的密文策略属性基加密方案,主要创新在于:访问树结构构造简单且支持与、或、门限操作,能实现灵活的访问策略。本文将访问树结构作为访问策略应用到格上属性基加密方案中,使访问结构更为灵活多样。
1 相关知识
1.1 格
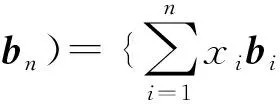

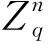


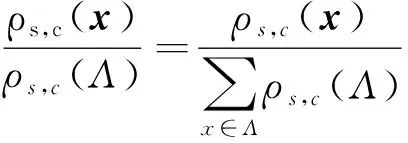
1.2 理想格
定义4环Zn的理想I又是格Zn的子格,称这个格为格Zn的理想格。具体定义如下:多项式环Z[x]/(f(x)),若满足以下3条性质。
1)f(x)的首相(最高次的项)系数为1;
2)在Z上是不可约的;
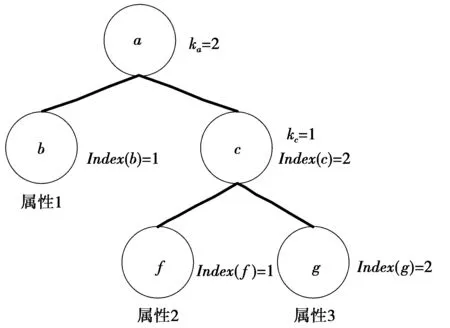
3)n的多项式函数用poly(n)表示,对环Z[x]上的任意多项式g(x)和h(x),都有‖g(x)h(x)·modf(x)‖ 树形访问结构T,根节点记为root,非叶子节点记为node。树中节点node的子节点个数记为numnode,节点node的父节点表示为parent(node)。树中每个非叶子节点都有门限值knode∈(0,numnode]。当knode=1时,该节点代表或门;当knode=numnode时,该节点代表与门。树中叶子节点node代表一个真实的属性,记为attr(node)。树中非叶子节点node的所有子节点用1到numnode进行编号,用index(node)返回。 Troot代表根节点为root的访问树,Tnode代表根节点为node的访问树。设置布尔函数Tnode(γ),其中,γ代表属性集合,当且仅当属性集合γ满足访问树Tnode时,有Tnode(γ)=1。若node为非叶子节点,令node′为node的子节点,当且仅当有knode以上个子节点的Tnode′(γ)=1时,节点node的Tnode(γ)=1。若node为叶子节点,当且仅当attr(node)∈γ时,Tnode(γ)=1。 图1为访问树结构的例子,图1中,节点a的门限值ka=2与子节点个数相同表示与门,节点c的门限值kc=1,即当有一个子节点满足即可,表示或门。树中叶子节点b,f和c分别代表属性1、属性2和属性3,当具有属性1和属性2或者属性1和属性3时才满足上述访问树。在方案中,根据访问树的设计可以实现灵活的访问策略。 图1 访问树实例Fig.1 Instance of tree-access structure Os:输出带噪声的伪随机采样样本(a,b)=(a,as+e)∈Rq×Rq,其中,a为环多项式,e是系数取自离散分布χ的噪声,s∈Rq是一均匀分布的密钥。 本方案包括如下4个算法。 1)系统初始化Setup(λ,U):授权机构初始化系统,输入系统安全参数λ和属性集合U,输出系统主私钥MSK,公布系统公共参数PP; 2)密钥生成KeyGen(MSK,ω′):授权机构执行密钥生成算法,输入主私钥MSK,根据用户属性集合ω′计算得到用户私钥K; 3)加密Encrypt(PP,M,T):该算法由发送方执行。发送者获取公共参数PP,采用访问树T作为访问策略,对消息M进行加密,计算出密文CT; 4)解密Decrypt(PP,CT,K):用户获取公共参数PP及密文CT,用自己的私钥K对其进行解密,得到明文M。 方案安全游戏模型为选择访问结构及选择明文攻击下的不可区分性。游戏方案由一个模拟器和一个敌手组成,具体如下。 Init:敌手提交给模拟器要挑战访问结构T*; Setup:模拟器运行初始化算法生成系统公共参数PP以及系统主私钥MSK,然后将PP发送给敌手; Phase 1:敌手可以询问任何不满足访问树T*的属性集合的私钥。模拟器根据敌手询问的属性集合生成私钥K,并将其发送给敌手; Challenge:敌手选择明文M发送给模拟器;模拟器掷一枚硬币b,如果b=0,则模拟器在密文空间中随机选择挑战密文C*;如果b=1,则模拟器生成挑战密文为C*=Encrypt(PP,M,T*),并将其发送给敌手; Phase 2:重复Phase 1; Guess:敌手提交对b的猜想b′。 Setup(λ,U):输入系统安全参数λ和属性集合U={u1,u1,…,un}。选择一个有效的大素数q=1mod(2λ)和一个小的正整数p,满足p< 1)随机均匀地选择主密钥SK0←Rq和元素a←Rq,计算PK0=a·SK0+pe0∈Rq; Encrypt(PP,M,T):输入公共参数PP,消息M和树形访问结构T,树中属性集合记为ω。随机选择s∈Rq。自上而下为树中的每一个非叶子节点node选择一个dnode=knode-1阶多项式qnode(x),其中,qroot(0)=s,其他每个节点的多项式要满足qnode(x)=qparent(index(node)),记qnode(0)=snode。根据叶节点的父节点取得叶子节点node的值,记为si∈Rq,i=attr(node)。 2)输出密文CT=(C0,{Ci}i∈ω,T)。 Decrypt(PP,CT,K):获取公共参数PP,用户的私钥K及密文CT。若用户属性集合ω′与访问结构T能够匹配,则可成功解密。定义递归解密算法DecNd(CT,K,node),其中,CT为密文,K为用户的私钥,node为树上的一个节点。通过递归算法DecNd(CT,K,root)对访问树T的根节点root解密,并加以处理计算得到明文M。递归解密算法DecNd(CT,K,node)具体如下。 1)如果node是叶子节点,则 DecNd(CT,K,node)=Ci·Ki= 2)如果node是非叶子节点,选择Inode,它是由节点node下满足访问树的最少子节点构成的集合,记节点node的子节点为z,则 利用本方案的加密算法将明文M进行加密,如果可以利用本方案的解密算法解密成功,得到明文M,则可证明本方案的正确性。 解密算法输出如下。 M*=C0-K0b= PK0rs+M+pe′-arts(SK0t-1+pe″)- PK0rs+M+pe′-ars·SK0- (a·SK0+pe0)rs+M+pe′-ars·SK0- pe0rs+M+pe′-arts·pe″- M=M*modp。 证毕。 定理1如果敌手能够以优势ε赢得2.2节中安全模型游戏,则模拟器可以有优势ε/2解决判定R-LWE问题。 Init:敌手提交给模拟器要挑战访问结构T*; Challenge:敌手发送给模拟器随机选择的明文串M。模拟器掷一枚硬币b,若b=0,则模拟器随机选择x0←Rq,计算C0=px0∈Rq和Ci=pxi∈Rq;若b=1,计算C0=pv0+M∈Rq和Ci=pvi∈Rq。然后将其发送给敌手; Phase 2:重复Phase 1; 表1 相关方案对比 文献[10-11,13]和本文方案中都是格上ABE方案,且这些方案加解密运算是线性运算,比传统的基于双线性对的ABE方案运算效率较高。从表1可以看出,文献[10-11]是基于标准格上的LWE难题,加密明文大小为1。文献[13]和本文方案是基于理想格上R-LWE难题,加密明文大小为n。文献[10-11,13]都是CP-ABE方案,分别支持门限、门限和LSSS访问结构。本文方案是基于理想格上R-LWE难题的CP-ABE方案,采用访问树结构支持任意的访问策略。在私钥尺寸上,文献[10-11]由级联矩阵利用左抽样算法进行密钥抽取,私钥大小和用户属性个数相关。本文方案与文献[13]的私钥是通过对环多项式计算得到的,由于m≥5nlogq,所以私钥大小远远小于文献[10-11]。在密文尺寸上,密文大小和格上相关方案[10-11]都与加密时访问策略中包含的属性个数相关,但由于m≥5nlogq,本文方案远远小于文献[10-11],与文献[13]保持一致。在密文膨胀率方面,本文方案远小于文献[10-11]。在计算效率方面,文献[10-11]中在计算密文时使用了n×m的矩阵以及m×m的矩阵,使得加密时的计算复杂度较高,加密效率低,加解密运行时间长。而本文方案和文献[13]在计算密文时,使用的是大小为n的环元素,计算复杂度较低,运算效率高,加解密运行时间短。从表2可以明显看出,本文方案的加解密效率与文献[13]的加解密效率相当,加解密效率远高于文献[10-11]。本文方案与文献[13]为密文策略属性基加密方案,且都基于理想格R-LWE难题,私钥大小、密文大小等性能相同。然而,文献[13]采用LSSS访问结构,构造相对复杂,而本文方案采用树形访问结构,灵活性较高,表达更为直观。 表2 加解密效率对比 本文利用理想格上的R-LWE问题构造了支持访问树结构的CP-ABE方案,证明满足选择访问结构和选择明文攻击下的安全性。方案采用树形访问结构,灵活性较高,同时利用理想格上的R-LWE问题可以加密n个比特的明文,系统效率较高。在实际应用中,属性基加密系统的属性会发生改变,这会引起属性的失效和变更等情况,下一步将对格上属性基加密机制中属性撤销问题进行研究。1.3 树形访问结构
1.4 环上误差学习问题



2 方案模型和安全模型
2.1 方案模型
2.2 安全模型
3 方案构造
3.1 系统初始化
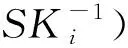

3.2 密钥生成

3.3 加密

3.4 解密

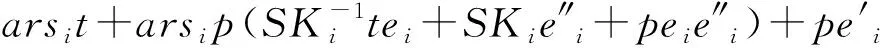
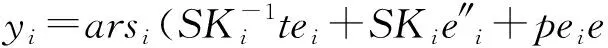
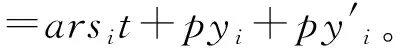
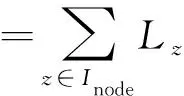
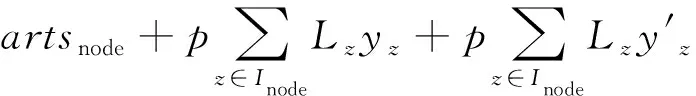

4 方案分析
4.1 正确性分析





4.2 安全性证明


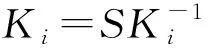

4.3 性能分析
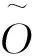


5 结束语

