基于多分布密度位置指纹的高效室内定位算法研究
乐燕芬,汤卓,盛存宝,施伟斌
(上海理工大学光电信息与计算机工程学院,上海 200093)
1 引言
随着物联网、移动智能终端的迅猛发展,位置相关的服务和应用受到了广泛的关注,尤其在无线传感器网络(WSN, wireless sensor network)相关领域,室内定位技术成为研究热点。由于GPS信号在室内复杂环境下迅速衰减,使得这种室外定位技术无法有效应用于室内环境。近年来,国内外学者对室内定位技术展开了大量的研究,其中基于接收信号强度(RSS, received signal strength)的方法不需要额外的硬件设备,具有成本低、易实现、非视距传输的特点,因而成为室内定位的重要实现手段之一[1-3]。
室内布局复杂多变,人员活动频繁,无线信号传播过程中存在多径效应、阴影效应,使信号的强度与传播距离具有较强的时变特性,并依赖于具体应用环境,很难找到能够准确刻画两者关系的传播衰减模型。针对于此,RSS定位算法中的一大类——位置指纹定位算法可用于解决上述问题,该方法需要预先确定监控区域内若干参考点位置RSS信号的分布,也称为位置指纹,目标节点通过RSS分布匹配来获取自身定位。定位过程一般分为离线训练和在线定位这2个阶段。首先在定位区域内布置若干个位置已知的节点,也称为锚节点(anchor node)。离线训练时,在定位区域内各参考位置点采集来自多个锚节点的RSS信号,并结合物理位置构成位置指纹;在线定位阶段,目标节点接收锚节点信号获取RSS值,利用模式匹配算法与位置指纹空间内的数据进行匹配,估计目标节点位置。
基于位置指纹的定位算法,不需要预设室内信号的传播衰减模型,定位精度取决于离线训练阶段与在线定位阶段的RSS信号是否符合相同的分布模型。而室内复杂的定位环境使RSS信号呈现较大时变特性,并不是信号越强的接入点(AP,access point)提供的定位精度越高[4],直接采用信号强度进行匹配,如radar系统采用的K最近邻算法[5],定位精度有限。为了有效挖掘 RSS信号的内在特征,目前很多研究工作集中在利用机器学习的方法对信号强度进行建模。如文献[6-7]利用基于核函数的岭回归方法获取参考位置与RSS信号的匹配模型,文献[8]则利用基于核函数的主成分分析法提取来自多个AP的RSS信号间的非线性特征,在此特征空间内进行匹配获得位置估计。这些方法有效地提高了定位精度,但存在的主要问题是定位阶段需要进行复杂的计算。如文献[8]进行在线定位时,接收到的RSS信号首先需要与所有参考位置点RSS信号进行核函数运算获得核矩阵,进行数据修正,以保证核矩阵数据中心化条件,在此基础上,求取该矩阵的特征值和特征向量,并最终获得该采样RSS的特征指纹,这一定位过程引起资源的大量占用,并不适用于移动节点主动定位的场合。
为减少定位阶段的匹配计算量,文献[4]提出了基于信息熵进行 AP子集选择的方法。在监控范围内所有能检测的 AP中,选择对所有参考位置点信息增益最大的k个 AP构成特征输入,并按照接收到的这k个RSS信号的相似度对参考位置点进行聚类。在线定位时根据接收到的RSS信号判定目标所属的簇,然后在该簇内利用决策树进行精确定位。这种算法不考虑参考位置点的物理位置,按AP子集的RSS信号进行聚类,有效地减少了定位阶段的计算量。但需要指出的是,AP子集的选择是基于监控范围内所有参考位置点接收的 RSS,考虑到 AP具有区域性,即同一个 AP对不同区域具有不同的信息熵贡献率,这种方法所选出的 AP子集对部分区域并不一定最佳,导致部分区域定位精度不高。文献[9-10]则考虑不同AP在同一位置的RSS具有相关性的特点,剔除包含冗余信息的AP,通过最优AP子集匹配完成位置估计。此类算法需要在定位阶段对收到的各个维度RSS进行高斯拟合,并计算各AP的RSS分布联合互信息,利用最小化互信息准则获取包含信息量最多的最优 AP子集。指纹匹配过程中,以 KL散度为标准计算待定位节点与指纹库中所有参考位置点的高维度高斯密度函数的相异度,并选择相异度最低的位置参考点作为位置估计。此类算法的优点是离线训练阶段数据库保留的 AP数量减少,降低了数据库规模,但在线定位阶段,所选的最优 AP需要与库中所有参考点的AP子集进行RSS分布差异度分析,时间复杂度较高。文献[11-12]分别在室内和室外环境下,利用目标节点与参考位置点是否接收相同AP集合的信号来判断两者的距离,来剔除不可能的参考位置点。而实际环境中,相距30 m的2个位置点接收的同一个锚节点的信号强度差值可能达到10 dBm,使这一方法只适用于粗定位。文献[13]则针对移动目标的运动状况和实际环境布局,建立基于位置的马尔可夫链来剔除不可能的位置跳变,这在实际应用中存在一定困难。当定位不是连续密集进行时,目标在较短的时间内可能越过多个参考网格,很难明确界定运动目标的物理可达范围,这在某种程度上限制了此方法的应用。
上述文献都试图通过最优 AP子集选择来减少位置指纹算法的计算复杂度或数据存储量,而在 WSN室内定位中,若参考位置点分布密度大或者由于定位区域广导致参考位置点分布数量大,则上述方法对定位性能的改善有限。同时考虑到室内环境复杂多变,无线信号传播特性与局部的物理空间密切相关,统一的选择策略并不一定局部最佳,因此提出了基于不同分布密度的位置指纹、精度渐进的室内定位算法,在保证定位精度的同时,降低定位的能耗、计算复杂度和存储空间。该方法把定位区域按锚节点的信号传达率分成若干局部空间,并按分布密度把参考位置点分成2类,分别为粗网格和细网格。定位时利用空间滤波法确定可能的局部空间集合,并利用主成分分析法(PCA,principal component analysis)[14-15]提取的粗网格的位置指纹特征匹配确定这些局部空间集合中目标节点可能所在的初步位置,最后利用WKNN(weighted K nearest nodes)方法完成细网格的精确匹配。所提出的方法兼顾了地理位置特征和RSS信号的分布特点,在降低运算量的同时保证定位精度。
2 算法的框架与原理
本文提出的多分布密度位置指纹定位算法,将大监控区域按照环境特点划分为多个局部空间,每个局部空间内选择若干个粗网格和分布相对密集的细网格。算法具体步骤如下。
步骤1离线训练阶段
这一阶段需要获取锚节点在每个局部空间的分布及粗、细网格的指纹特征。
1) 为每个局部空间建立锚节点信号的覆盖向量。该覆盖向量具体描述了在特定的物理环境下各锚节点在每个局部空间的信号分布。
2) 在局部空间内选择若干粗网格,通过 PCA训练离线RSS信号,获取可描述粗网格特征的指纹数据库。
3) 在每个局部空间的细网格点采集RSS信号,获取描述细网格的位置指纹。
步骤2在线定位阶段
这一阶段,目标节点实时采集来自锚节点的RSS信号,完成自身定位。
1) 采用空间滤波法确定目标节点可能的局部空间。采集RSS信号获得动态覆盖向量,与各局部空间的覆盖向量进行比较,选择汉明距离较小的若干局部空间作为可能区域。
2) RSS信号经PCA变换后获取主成分,与局部空间内的粗网格的指纹数据特征进行匹配,选择欧式距离最小的若干粗网格作为目标节点的位置范围。
3) 在粗网格内,采用WKNN方法,选取匹配度最高的K个细网格加权平均后作为估计位置。
上述方法中,离线阶段不需要增加样本采集数量,在线定位阶段节点的计算量主要集中在粗、细网格的匹配过程,但不需要与定位区域全部指纹进行匹配,减少了节点对资源(包括存储空间、能量)的消耗。
2.1 空间滤波法
位置指纹定位是利用室内空间内,尤其存在墙壁遮挡等情况时,RSS信号的衰减体现出很强的空间性。空间滤波法综合考虑物理空间的具体情况和信号衰减特性之间的相关性,认为目标节点与网格点越接近,则两者接收到的RSS信号越相似,利用这一特性完成局部空间的粗定位。
局部空间内的RSS信号分布用覆盖向量C描述,CM=[IM1,IM2,…,IML]是第M个局部空间的覆盖向量。如果在该局部空间内能连续接收到第i个锚节点的RSS信号,则IMi=1,否则IMi=0。具体实施时,离线训练阶段的连续接收可以定义为:该锚节点的信息可以被该局部空间内随机运动的节点在90%的采样时间内接收到或在90%的细网格接收到。
覆盖向量C为二进制数据类型,因此适合采用汉明距离来表征2个向量间的差异大小,若目标节点定位过程中接收的 RSS信号分布向量为C′,则

通过式(1)对所有局部空间进行匹配,若dH(CM,C′)<αL,则该局部空间作为候选空间。参数α(0 <α< 1)的大小影响算法的复杂度和定位的准确度。若α过大,则空间滤波性能不佳,可能引入较多的无效区域;若α过小,在RSS存在较大时变时,可能漏掉有效区域。α的选择应参考实际应用环境RSS的时变情况。
通过空间滤波,目标节点可能的局部空间集合定义为P′={CM,dH(CM,C′)<αL},且|P′|=M′。下面将通过 PCA提取粗网格的特征,通过特征匹配确定目标节点处于局部空间集合P′的那些粗网格内。
2.2 PCA粗定位算法
在大监控区域内可能布置较多的锚节点,目标节点在某一位置可能同时接收到10多个锚节点的信号。常用的降低定位算法计算复杂度的方法是按某种策略选择最优AP或锚节点集合。不同于以上方法,PCA经过线性变换从来自各锚节点的 RSS信号中提取包含原始信息的少数几个综合指标,这些指标互不相关,也称为主成分,在降维的同时保持了信号变量的总方差不变。PCA变换可用式(2)表示。

其中,S=[s1,s2,…,sL]代表目标节点定位中实时接收到的L个锚节点的 RSS信号,若无法接收某个锚节点的信号,则相应的值设为最小值-95 dBm;是变换后获取的主成分;变换矩阵A是L×K维矩阵,表明了每个锚节点RSS对主成分的贡献量。从式(2)中可看出,PCA在降维时并没丢弃原RSS数据,而是融合了所有锚节点的信息。文献[11]的研究也表明该方法可有效提高定位精度。值得说明的是,PCA提取的是数据间的线性特征,而二阶以上的高维非线性关系需要通过其他方法,如基于核函数的PCA来提取[8],但后者定位阶段涉及复杂的计算,因此,本文使用PCA训练RSS数据,获得线性变换矩阵A,把S′作为局部空间内粗网格的指纹特征,把目标定位到某一粗网格内。
2.2.1 粗网格的PCA变换
设整个定位区域划分为多个局部空间,每个局部空间内有若干个粗网格,共有N个粗网格。离线阶段在每个粗网格上采集来自L个锚节点的RSS信号,将多次采集的RSS均值作为该粗网格li(xi,yi)的原始位置指纹信息Si=[s1,s2,…,sL]T。全部粗网格的原始位置指纹构成了一个N×L维的矩阵S,相当于L维的N个训练数据。在进行PCA变换前,首先保证数据空间满足中心化的条件,对S按式(3)进行调整。
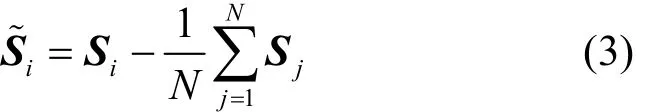
根据式(4)计算数据空间的协方差矩阵CΓ。

协方差矩阵CΓ的特征值{λ1,λ2,…,λL}和特征向量{V1,V2,…,VL}满足

将特征值从大到小排列,并取前K个最大的特征值λ1>λ2>…>λK及对应的特征向量V1,V2,…,VK。
PCA保证所选择的转换矩阵A使得
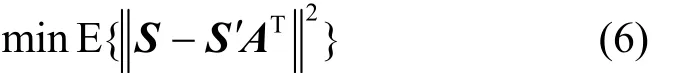
此时满足

这样,通过PCA处理,原始位置指纹S包含的RSS信号变换为包含K个主成分的S′特征位置指纹。
2.2.2 粗网格定位
在线定位阶段,目标节点采集各个锚节点的RSS信号F=[rss1,rss2,…,rssL],通过矩阵线性变换,获得表征其主成分的特征指纹F′=FA。假设空间滤波后匹配的局部空间内共有M个粗网格,则计算F′与粗网格特征指纹S′的欧式距离,如式(8)所示。其中,Dj(F′,S′j)表征F′与第j个粗网格的相似程度,其值越小,两者越相似。取Dj(F′,S′j)值最小的粗网格作为目标节点初步估计位置。
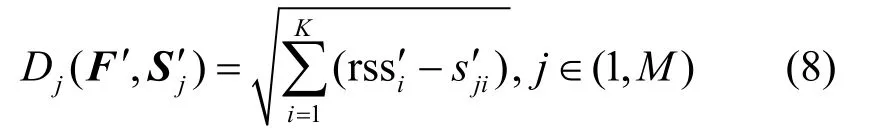
2.3 细网格匹配
细网格的匹配也是定位的最终阶段,可以根据具体应用选取目前已有且定位精度较高的方法,如基于核函数的 PCA方法、基于贝叶斯最大估计的后验概率估计法等。由于粗定位已经把目标锁定于粗网格,因此不管采用何种方法,在线定位阶段均不涉及大量的运算。需要说明的是,这些方法均使用高斯模型来描述室内复杂环境对 RSS可能产生的误差[15-16],同时离线阶段的工作量仍然较大,如基于核函数的 PCA方法,需要完成细网格点的特征提取,而基于后验概率估计的定位方法,则需要利用最大似然估计完成每个细网格点的高斯分布参数。本算法采用 WKNN方法,离线阶段需要采集RSS作为原始指纹,而不需要其他额外工作,在线阶段则只需计算目标节点采集的 RSS与匹配粗网格内细网格的欧式距离,选取距离最小的R个细网格位置的加权平均作为目标节点的最终位置估计,如式(9)所示。

其中,w是目标节点估计位置;wr是选取的R个匹配的细网格位置;Pr代表wr网格归一化的权重系数,表示为

其中,Di(F,Si)是目标节点采集的RSS信号F与第i个细网格点的原始位置指纹S的欧式距离。
3 实验结果及分析
3.1 实验设置
为了评估本文所提出定位算法的性能,在上海理工大学光电大楼进行了数据采集和定位实验。实验区域为第9层的大厅和走廊位置,大小为36 m×14 m。其中,大厅中有会客沙发、自习桌椅等物体,且有较多的人员走动;目标定位区域均匀划分为1.8 m×1.8 m大小的90个网格。两侧走廊以4.2 m为间隔均匀布置了共18个锚节点。对每个网格点进行2 min的RSS信号采集,从中随机抽取10个RSS观测向量,将其均值作为测试数据;其余的RSS观测向量均值处理后作为原始位置指纹数据。信号采集过程中,可以观察到由于电梯井、楼梯房间墙壁等的阻挡以及人员走动等因素,在网格点收到的RSS信号并不是均匀地来自所有锚节点。有的锚节点能收到100多次信号,而有的只有30多次信号,甚至有些网格点会无法收到部分锚节点的信号,并且表现为持续性无法接收,这些未接收到的RSS信号统一用最小值-95 dBm填充。
图1给出了在某一测试点获取的来自同一个锚节点的RSS信号分布直方图,图中的曲线是RSS信号分布的概率密度函数。从图1中可看出,即使在同一位置,来自同一个锚节点的RSS也是随时间变化的。
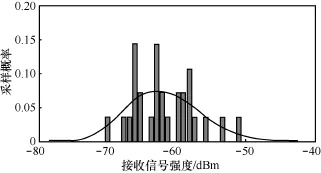
图1 RSS信号分布直方图
3.2 定位性能评估
3.2.1 空间滤波对定位精度的影响
根据 RSS信号的分布特点并结合定位物理环境,实际目标定位区域分为5个局部空间,对应的覆盖向量为C=[C1,C2,C3,C4,C5]T。如1#区域C1=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1]表明此区域内的网格点无法接收到 15#和 17#锚节点的信号。随机抽取30个网格点的测试数据进行空间滤波,结果如表1所示。

表1 局部空间匹配结果
由表1可以看出,当设定覆盖向量C汉明距离dH=0,也即要求覆盖向量完全匹配,22个网格点确定了唯一的所处局部空间,还有8个网格点与5个局部区域的覆盖向量都存在汉明距离,无法判定所处的局部区域。随着汉明距离的增大,匹配的局部区域数也增多。当汉明距离为5时,其中有23个网格与3个局部空间的汉明距离小于或等于5,甚至有2个网格与所有局部空间的汉明距离都不大于5。因此在本定位区域内,dH选择2,通过空间滤波,使得目标节点初步定位在1~3个局部空间内,有效地减少了指纹匹配量。
3.2.2 粗网格定位性能分析
针对实验中目标定位区域的具体环境特点,1#、2#、4#和5#局部区域不再划分粗网格,也即每个局部区域本身就是一个粗网格,并设置2个参考位置点;而3#局部区域即大厅13 m×14 m的空间内划分2个粗网格,每个粗网格内设置8个参考位置点。实验时在粗网格内的参考位置点各采集 80次RSS信号,由此产生1 920个训练数据用于PCA分析,获得变换矩阵A和18个特征值。
图2给出了实验中获得的RSS信号提取的特征值,18个锚节点对应18个特征值。特征值越大,说明相应的主成分包含的原始信息越多。根据特征值的信息贡献率,可确定提取的主元个数。实验中选取9个主元,此时

图2 粗网格PCA变换后提取的特征值

即 9个主元提供的信息占原 18个锚节点的 RSS所包含信息的90%以上。因此实验中的转换矩阵A是18×9维的矩阵,粗网格内参考位置点的指纹由S=[s1,s2,…,s18]变换为S′=[s′1,s′2,…,s′9]。在线采集的RSS信号F=[rss1,rss2,…,rss18]经PCA 变换为F′。
3.2.3 定位性能评估
实验采用定位的平均误差ME(mean error)和定位误差的累计密度函数(CDF, cumulative density function)作为标准来评估算法的性能。
图 3给出了本文提出的 A-WKNN算法与WKNN算法、InfoGain[4]算法、Bayes-PCA算法[15]的累计误差分布函数。其中本文的算法空间滤波中参数dH=2,匹配粗网格数为4,匹配细网格数为4,加权平均后作为估算位置;WKNN算法中选取4个最近邻细网格点加权平均后作为估算位置;InfoGain算法则从18个锚节点中提取信息熵最大的10个锚节点的RSS作为特征;Bayes-PCA算法对所有的细网格进行 PCA变换获得特征指纹库,再选取后验概率最大的4个细网格加权平均后作为估算位置。

图3 4种定位算法误差累计分布
实验结果表明,WKNN算法平均定位误差为1.91 m,InfoGain算法平均定位误差为 2.28 m,Bayes-PCA算法平均定位误差为1.74 m,本文所提算法平均定位误差为1.82 m。结合图3可知,本文提出的算法在降低能耗时并未牺牲定位精度。此外也采用文献[8]中提出的 Kernel-PCA算法进行了定位。根据本实验定位区域 RSS信号的实际分布特点,算法中高斯核宽度ε取2,提取20个特征,实验结果与文献所报道的定位精度存在很大差距,这可能是由于实验场景不同使得RSS特征不一致或参数未优化而导致。
实验中也发现,由于特征值贡献率的不同,主元数量K的选择对定位性能有很大的影响。主元数量过多使计算量增大,而过小则可能会损失较多的原始信息。图 4给出了选取不同主元数量时的PCA重建误差,误差计算如式(6)所示。当主元数在7个以上时,重建误差小于35,意味着这几个主元可以较好反映原 RSS信息。不过值得一提的是,RSS信号与环境密切相关,当环境中存在很强的非线性噪声时,PCA可能因无法剔除噪声而不能有效提取信息。

图4 原RSS信号与PCA重建信号之间的误差
图5给出了进行PCA变换时选择不同主元数量对定位精度的影响。从图5中可看出,主元数量与定位精度两者并不是正相关的关系,当采用过多的主元时,数据在这些主元方向都进行了投影,反而模糊了信号特征之间的差异。实际应用时应根据锚节点的数量选择合适的主元数量,以达到最佳的特征提取,同时兼顾系统定位精度和计算量的要求。
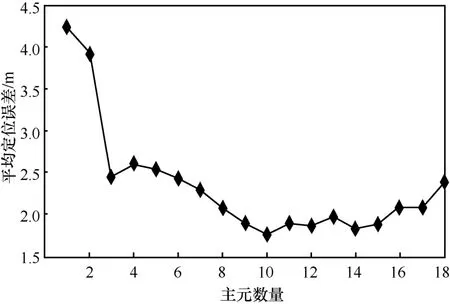
图5 PCA变换中取不同主元数量对定位精度的影响
在指纹定位算法中,锚节点的分布密度是影响定位性能的重要参数。本实验中大厅走廊两侧共布置了 18个锚节点,不考虑位置分布对定位性能的影响,实验中考察了布置6个、10个、14个和18个锚节点时定位性能的变化。由于锚节点的数量变化,相应的主元个数也需要调整。图6给出了不同锚节点和不同主元数量时算法的定位性能。

图6 定位平均误差随锚节点数和主元数变化的情况
图6中可以看出,锚节点数量与定位精度之间并没有确定的相关性。具体分析如下,在布置 18个锚节点的情况下,主元数量为 10时,定位平均误差为1.81 m;在布置10个锚节点,主元数量取6时,定位平均误差为1.89 m;而在取5个主元数时,10个锚节点的情况定位误差最小。这说明通过选择合适的主元数量,锚节点数量的变化对本方法的定位精度影响不大。实际应用时,选择合适的锚节点数量,可以在保证定位精度的同时大幅降低定位计算量,减少节点能耗。
4 结束语
基于 RSS的指纹定位技术,从减小定位计算量、降低能耗的角度提出了一种基于不同分布密度指纹的室内定位算法。该算法考虑到某些室内环境中既有相对空旷的空间,又有众多墙体等障碍物或狭长走廊等复杂的环境特点,结合实际物理环境和RSS分布,把定位区域划分为多个局部区域及相应的RSS信号覆盖向量。在局部区域内又设定稀疏分布的粗网格,离线阶段通过 PCA提取特征主元作为粗定位的位置指纹数据;在线阶段通过覆盖向量及 PCA线性变换确定目标节点的初步位置,再利用 WKNN算法由分布相对密集的参考位置点确定最终的估算位置。实验表明本文提出的算法在有效减少定位阶段节点能耗的同时保持了定位精度,同时降低了锚节点的分布密度对定位结果的影响。但本实验还未实现针对更大定位区域及移动目标的实时定位,这也是本算法下一阶段的研究目标。

