基于压缩感知的双麦克风混响多声源定位算法

张奕，李娟，张敏

（大连大学信息工程学院，辽宁 大连 116622）

1 引言

目前，在视频会议、智能机器人、车载电话、语音增强等领域中，基于麦克风阵列的声源定位技术现已得到广泛应用[1]。传统的声源定位算法主要基于以下3种：1） 基于波束形成的定位算法，该算法采用波束形成技术，通过调节麦克风阵列的指向对整个接收空间进行搜索，使阵列波束对准声源而获得最大的输出功率[2]；2） 基于高分辨率谱估计的定位算法，通过求解阵列接收信号的协方差矩阵获得空间谱函数，再由此信息进行声源定位，使用较广泛的算法有 MUSIC（multiple signal classification）、ESPRIT（estimating signal parameter via rotational invariance techniques）、子空间拟合等[3]；3） 基于到达时延差的方法，此为当前应用最广泛的一种定位方法，该算法根据声源信号到达不同位置麦克风的时间差，计算出声源位置相对于多组麦克风所在的多个双曲面，其交点就是声源的位置[4]。然而传统的麦克风阵列声源定位技术都无法摆脱三角定位的限制，在混响环境下受到更大挑战，即使采用信道盲分离技术，可恢复的空间声源数目也无法超过麦克风数量，这使得现有的具有实用价值的麦克风阵列系统都是海量阵列。

压缩感知（CS, compressed sensing）理论提出以后，很多学者将其引进到语音信号处理的多个领域中。例如，Asaei 利用结构性稀疏的压缩感知框架来进行多说话人语音识别，实现了4个麦克风以95%的正确率识别9个说话人[5]。Wabnitz利用压缩感知框架进行三维空间声场重构，极大地减少了数据集的处理量，并扩大了听觉甜点的范围[6]。Benichoux利用压缩感知技术，突破了全房间冲激响应估计中麦克风数量大于等于声源数目的限制[7]。Mignot利用压缩感知技术通过低频插值来恢复房间的全冲激响应[8]，仅采用120个麦克风的空间采样点即可恢复全房间冲激响应，极大地减少了麦克风的使用数量。Chardon采用MMV（multi- measurement vector）框架，利用随机稀疏字典构造广义MUSIC算法进行多声源识别和定位[9]。广义MUSIC算法在较少麦克风情况下仍可取得理想定位效果，但该算法基于理想模型假设，只适用于线性阵列。

文献[10]基于压缩感知框架，提出了使用麦克风阵列定位单个声源的定位算法。该算法假设麦克风阵列和声源处于同一水平面，将声源可能存在的空间离散成I个位置，并以这I个位置的房间冲激响应来构建字典，再采用OMP（orthogonal matching pursuit）算法恢复出声源信号矢量，则矢量中最大元素对应的位置即为实际声源的位置。相位变换加权的可控响应功率（SRP-PHAT，steered response power-phase transform）[11]定位算法通过搜索空间中使SRP（steered response power）函数最大的点作为声源的估计位置，该类算法对混响的顽健性较强，但在多声源条件下会受到各声源之间的相互影响，使传统的 SRP-PHAT算法的多声源定位性能并不高。文献[12]对此做出改进，提出了基于子带可控响应功率的多声源定位算法（SRP-sub，sub-band steered response power），该算法对语音信号频谱进行划分之后，在每个子带寻求SRP的最大值以定位声源。以上算法虽然都能在混响环境下达到声源定位的目的，但要取得显著的定位效果，所采用的麦克风数目必须远多于空间中声源的数目。

本文基于压缩感知框架，结合房间混响所带来的空间信息来构建室内混响环境下采用双麦克风进行多声源（至少3个声源）定位的模型。该模型将混响环境下的多声源定位描述为多点声源经由房间冲激响应模板压缩到麦克风的压缩感知问题，从而提出了一种基于压缩感知的双麦克风混响多声源定位算法。由于在本文的研究框架下，多点声源相对房间的整个空频域而言呈现块稀疏特性，而块稀疏所需的观测量（麦克风数目）要比普通稀疏的观测量少得多，故对块稀疏信号的求解使得使用欠定数量（麦克风数目小于声源数目）的麦克风阵列定位多声源成为可能。

2 混响多声源问题描述

室内混响环境下，声源数目未知的多声源多信道的时域模型为

其中，xm表示第m个麦克风接收的信号，表示第n个声源信号，表示第n个声源与第m个麦克风之间的房间冲激响应，*为卷积符号，M为麦克风的数量[13]（本文中M=2）。经短时傅里叶变换得到式（2）。

3 基于压缩感知的双麦克风混响多声源定位算法介绍

3.1 压缩感知理论

假设N×1维的矢量在稀疏基上有如式（3）的表示。

则称在稀疏基ψ上，信号Z是稀疏的。其中矢量S中非零值的个数为k，也被称为稀疏度，且

压缩感知理论指出，若矢量Z本身稀疏或者其在某一已知基ψ上的系数呈现稀疏性，则可通过一个维的压缩观测矩阵Φ将矢量Z线性投影到一个低维的观测矢量X中[14]，其中该线性投影可以表示为其中A被称为 CS矩阵，

当 CS矩阵A满足有限等距约束时，通过低维的观测数据可以高概率重构出原始信号[15]。信号Z稀疏或Z在某个基上稀疏的情况下，欠定方程组X=AS可以通过l0范数最小化约束来求解[16]，即

由于l0范数求解属于非凸问题，一般采用范数近似地对S的稀疏性进行约束而取得更好的重构效果。

根据CS理论，信号重构可以看作是在一定条件下的优化问题。现有的重构算法主要基于以下三类[17]：第一类为贪婪迭代算法，主要有匹配追踪（MP，matching pursuit）算法、正交匹配追踪（OMP，orthogonal matching pursuit）算法等[18]；第二类为凸优化算法，常用的有基追踪（BP，basic pursuit）算法[19]；第三类是基于贝叶斯框架提出的算法[20]。

3.2 块稀疏表示

为简化问题，本文将房间看作二维平面（俯视面），将该平面区域分割成G个网格[21]，每个声源最多只占据一个网格。假设房间中存在K个声源且在时间观测窗内声源位置不变，在每个网格g处选取F个频点，即并将所有网格点的频点数据按列堆叠成一维向量。该方法同样适用于三维空间，只需要将三维空间划分的网格平铺到一维即可。当空间中只存在K个声源时，理论上有声源的网格对应的在频点处就会出现非零值。如图1所示，房间被划分成G个网格，黑色网格表示声源所在位置，其频域表示如图1右侧所示，而其他没有声源的网格在各频点的值均为 0。这使得多个声源信号的空-频域表达S具有某种结构稀疏性，由于在这一结构中，非零元素成块出现，故也称声源信号在空-频域上具有块稀疏性，即有几个说话人（声源）就对应几个非零块，块的大小等于选取的频点数。

3.3 构造压缩观测矩阵

假设已知房间为有限阻抗墙壁组成的矩形封闭结构，则可利用Image方法[22]构造房间中任意空间点声源到达某一空间位置麦克风的房间冲激响应。Image方法又叫镜像法，麦克风接收到的声源信号包括了直达声和经多次反射后的信号，Image方法与光的镜面反射特性相似，将反射的信号看成是墙壁另一侧的虚声源传播到麦克风的信号。考虑到多径效应，则网格g处到第m个麦克风的投影可采用Green函数表示，如式（5）所示。

图1 具有块稀疏结构的声源位置分布的空-频域示意

l为第r次反射的反射系数；α为衰减常数，在球面传播模型中，α=1；c表示声速[23]。采用式（5）的声源-麦克风投影构造F个频点的频域投影矩阵为

则所有网格点经由房间投影到第m个麦克风对应的压缩观测模板为

所以麦克风阵列对应的压缩观测模板为

将Φ′按列归一化后得到压缩观测矩阵如式（9）所示。

3.4 本文提出的定位算法

基于以上描述，本文算法整体流程如下。

1） 采用Image方法产生全房间冲激响应，并根据式（6）～式（9）完成压缩观测矩阵Φ的构造。

2） 利用压缩感知框架描述语音定位问题，并采用块稀疏优化算法恢复出声源信号的估计

综上，使用双麦克风对多个声源进行定位的问题可表示为求解线性方程组，如式（10）所示。

式（3）写成矩阵的形式为

式（10）中，等式左侧项表示 2个麦克风接收的信号在不同频点的值，其中，下标 1、2为麦克风编号，即第一个麦克风和第二个麦克风。等式右侧第一项为根据式（6）～（9）选取的F个频点构造的压缩观测矩阵，第二项为各个网格点的信号在频域的表示，每个网格各取F个频点。理论上，有声源的网格对应的频点值存在非零值，而无声源的网格处，其所有频点值对应为零值；即空间中声源的位置和式（11）信号S中的非零块所在的位置之间存在一一对应的关系，故估计空间中多声源的位置问题可转换为确定非零块在S中的位置问题。

要确定S中的非零块需要先通过求解式（10）的欠定线性方程组来获得声源信号的估计为简化问题描述，在本文的双麦克风定位研究中，假设使用频点数为2，声源数目为3，麦克风数为2，并将房间划分为4个网格，则式（10）可以简化为式（12）。

对于求解如式（12）所示的欠定线性方程组，如果仅从普通稀疏优化的角度，即基于l0范数优化的角度，信号S的维度n=8,非零变量个数为6（稀疏度k=6），则至少需要m=6个观测数据才能恢复；如果采用基于l1范数的优化算法，则需要满足更严格的 RIP（restricted isometry property）约束条件，所需的观测数据量因此，式（12）的4个观测数据采用普通稀疏优化时，无法唯一恢复信号，即采用普通稀疏算法时，无法仅使用2个麦克风定位3个声源。然而，如3.2节所述，由于该声源信号在空-频域具有结构稀疏性，所以，当对其进行块结构约束时，对于信号S的N=4个块中，非零块K=3，每个非零块大小d=2，则采用块稀疏优化算法（基于l0范数优化）只需3个观测数据即可得到该3个非零块的全部数据；若采用基于l1范数的优化算法，则需满足 block RIP,即观测数据量最少满足可见块稀疏所需的观测量是普通稀疏数据量的此时2个麦克风可以定位3个声源，即采用块稀疏优化时，式（12）可解。所以，式（10）的欠定线性方程组可采用块稀疏约束求解。

本文采用 ReGOMP（regularized group orthogonal matching pursuit）[24]块稀疏重构算法求解，这是 Majumdar提出的一种结合了正则化正交匹配追踪（ROMP，regularized orthogonal matching pursuit）算法[25]和块正交匹配追踪（BOMP，block orthogonal matching pursuit）算法[26]的针对块稀疏信号的重构算法。该算法在每次迭代时首先挑选出与残差最匹配的K个块，然后在正则化过程中筛选出其能量介于最大能量与最大能量的一半之间的块集合作为候选支撑块集合。正则化过程提高了筛选的准确性，同时相比BOMP算法每次只选择一个支撑块，ReGOMP算法每次选取多个支撑块，加快了收敛速率，解决了ROMP算法不能解决的块稀疏问题；其缺点是块稀疏度必须先验已知。

在使用ReGOMP算法求得声源信号的估计ˆS后，根据选取的频点数F重新整合分块。如式（13）所示，对每F个频点求解其l2范数，则非零范数（非零块）在ˆS中的位置对应的就是空间中声源所在网格点的位置。

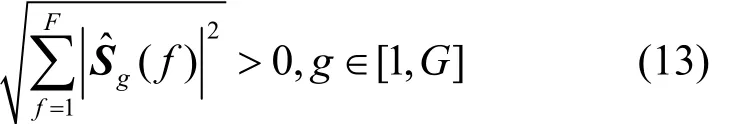
4 仿真实验与分析

为进一步验证上述所提出的算法的有效性，本文使用Matlab 2014b进行软件仿真实验。首先对不同说话人同时位于房间不同位置时的情况进行双麦克风定位模拟，然后分别就混响时间RT60对定位成功率的影响，频点数F的变化对定位成功率的影响以及可定位的声源数目增加时算法的定位性能进行讨论，并分别和文献[12]的多声源定位算法SRP-sub进行仿真实验对比，最后从平均运行时间的角度分析了本文算法的复杂度。

4.1 实验设置

仿真使用的矩形房间为3.3 m×4.4 m×2.5 m（长×宽×高）。分别以0.3 m×0.4 m为间隔将房间二维平面划分为10×10的网格，2个全向麦克风位置坐标分别为[1.6,1.6,1.7] m和[1.4,1.9,1.7] m。假设说话人与麦克风阵列处于同一水平面，采样频率,声速c= 343m/s ,墙壁反射系数为0.7，采用Image方法产生全房间冲激响应，长度约为2 500点，统一截取前1 000个频点的值，在频域进行2 048点的傅里叶变换，并等间隔选取F个频点构造压缩观测矩阵。

图2模拟了不同说话人（声源）同时位于房间不同位置时，采用本文算法和文献[12]算法的定位情况。混响时间RT60=0.3s，频点数F=80。

从图2可以看出本文算法对多声源定位的优势。SRP-sub算法虽然采用子带划分的思想来避免多个声源距离较近时出现易混淆的现象，但在麦克风数量少于声源数目时，表现依然乏力。所以，在一定的误差条件下，使用双麦克风在混响条件下进行多声源定位是可行的。

4.2 混响时间RT60的影响

本实验中，混响时间RT60分别取0.2 s、0.3 s、0.4 s、0.5 s、0.6 s产生全房间冲激响应，等间隔取个频点构造压缩观测矩阵，并分别采用本文算法和SRP-sub算法进行多声源定位，两者在不同混响时间下的定位结果如图3所示。由图3可知，当混响时间增加时，本文算法的定位能力不但没有降低反而略有上升的趋势，可见本文算法对混响时间的顽健性。而SRP-sub算法在多声源情况下本身定位性能不高，高混响更是严重影响了其对多声源定位的能力。

4.3 频点数F对定位性能的影响

参考4.2节的仿真结果，取混响时间RT60=0.3s，统计频点数F取值为 20、40、60、80、100、120时分别采用本文算法和SRP-sub算法对多声源的定位成功率，其结果如图4所示。

由图4可知，随频点数的增加，本文算法的定位成功率逐渐提升，但超过某一频点数时，其上升趋势渐趋缓慢。这是因为本文算法在信号重构之后需要再整合F个频点的能量信息来进行分块，当频点数达到一定数值时，由于这些频点已经包含了整个信号的绝大部分能量，所以继续增加频点数目，对算法的定位性能提升较少。而对于SRP-sub算法，由于其每个子带的SRP函数也依赖于各频点的值，所以频点数的增加也使SRP-sub算法的定位性能得到提升，但整体而言，本文算法在双麦克风条件下的多声源定位性能远高于SRP-sub算法。

图2 不同说话人同时位于房间的不同位置

图3 不同混响时间下的定位成功率

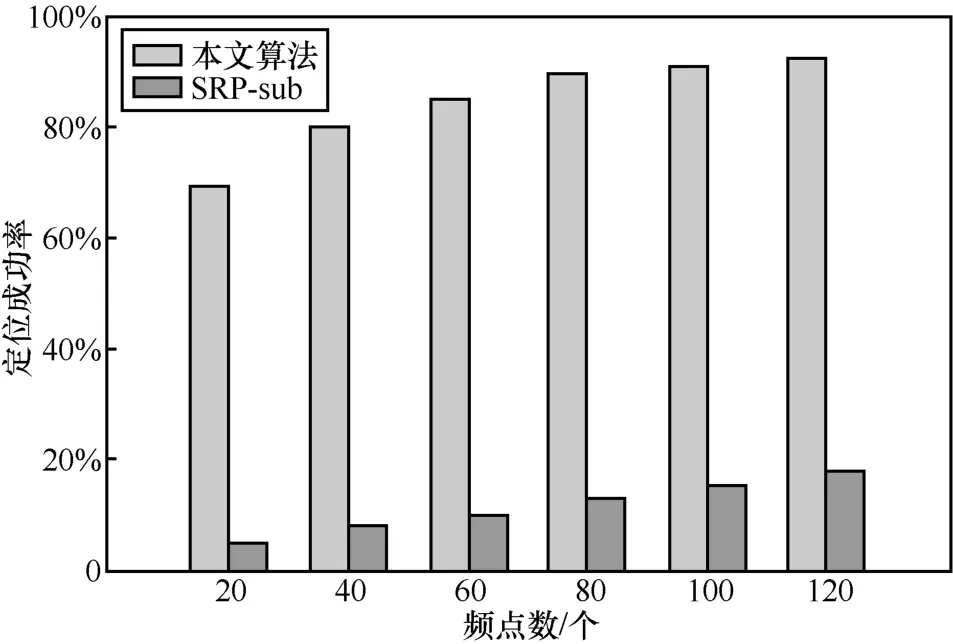
图4 频点数对定位成功率的影响

4.4 可定位的声源数目增加时的定位情况

参考4.2节与4.3节的仿真结果，设置混响时间RT60=0.3s，频点数F=60，在可定位的声源数目分别为3、4、5、6、7时，分别采用2种算法进行定位仿真实验，其定位成功率统计结果如图5所示。

图5 可定位的声源数目与对应的定位成功率

由图5可知，在以上混响时间和频点数条件下，使用本文算法定位 3～4个声源的结果是可以接受的，而SRP-sub算法在同等条件下表现较差。尽管对于更多声源的情况，本文算法未能取得很好的效果，但整体性能依然优于SRP-sub算法。同时本文的算法很好地说明了混响环境下欠定数量（麦克风数量小于声源数量）的麦克风阵列多声源定位的可行性和潜力，这对体积受限的通信设备来说具有极大的研究价值。

4.5 算法复杂度分析

本文的定位算法中，假设全房间冲激响应已知，故不考虑计算压缩观测矩阵的时间，这样算法的运行时间仅是利用 ReGOMP算法恢复块稀疏信号的时间与对该信号整合分块的时间之和。图6记录了在不同频点数和块稀疏度时，使用双麦克风定位1 000次的平均运行时间。由于本文的块稀疏优化算法的稀疏度为先验已知的，实验中块稀疏度等于声源数目，所以在不同块稀疏度时的运行时间可认为是不同声源数目时的运行时间。

由图6可知，频点数取值在20～80时，块稀疏度（声源数目）增加，本文算法的平均运行时间只是略微增加；频点数取值100～120时，本文算法的平均运行时间随块稀疏度的增加增幅稍大。图6也反映了频点数对算法的运行时间的影响比块稀疏度对运行时间的影响更大。但通过4.3节的实验也说明了当频点数超过一定数值时，算法的定位性能提升幅度较小，所以可酌情选择频点数目，使得在保证一定的定位成功率的情况下，运行时间不至于很大。

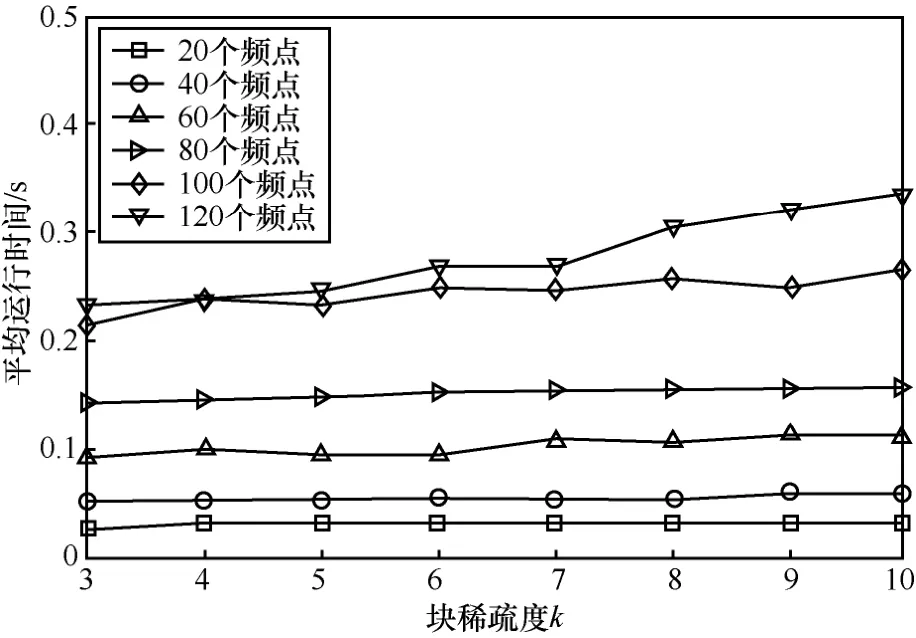
图6 算法在不同块稀疏度和频点数时的平均运行时间

5 结束语

基于麦克风阵列的声源定位技术是阵列信号处理领域的一项研究热点，而压缩感知的出现又为该领域的发展提供了一个崭新的视角。本文提出的基于压缩感知的双麦克风阵列混响多声源定位算法以归一化的全房间冲激响应为特征，构建压缩观测矩阵，将多声源定位问题转化为块稀疏信号的重构问题，通过重构信号的块与空间声源的对应关系得到实际声源的位置。

该算法不仅能解决室内混响环境，如会议室、小型会议场等的定位问题，且麦克风数量的减少可大大减轻系统的运算负担和硬件成本。本文仅使用2个麦克风就能对混响空间中至少3个声源进行定位，其中声源数目为3～4个时，定位效果较好。虽然本文算法对于更多声源的定位情况不是很理想，但依然摆脱了传统声源定位算法中，麦克风数量必须大于声源数目的限制。这对于室内混响空间中小型化的便捷语音设备而言很有研究价值。