基于干扰观测器的永磁同步电动机滑模控制

颜渐德，王 辉 ，兰永红，罗胜华

(1.湖南大学,长沙 410082; 2.湖南工程学院,湘潭 411101;3.湘潭大学,湘潭 411105; 4.湖南电气职业技术学院,湘潭 411101)

0 引 言

永磁同步电动机(以下简称PMSM)因其具有能量密度高、效率高、可靠性高等优点，在交流驱动系统中得到广泛的应用。然而，PMSM是典型的多变量和强耦合的非线性系统、存在参数摄动、外部干扰等不确定因素，导致PMSM控制系统的动态性能下降。如何寻求有效的控制策略，克服PMSM系统的外部干扰以提高系统的性能，引起了国内外学者的广泛关注[1]。

近年来，许多学者在提高PMSM的速度跟踪性能上，提出了许多控制策略，如：矢量控制[2]、反推控制[3-4]、自适应控制及无源控制等[5-7]。文献[4,8]针对PMSM矢量控制系统，通过构造新的子系统，并选取合适的虚拟变量和虚拟控制函数，利用李雅普诺夫稳定性理论设计控制量，从而使系统具有全局稳定性，实现良好的系统跟踪。滑模变结构控制算法简单、鲁棒性好和可靠性高，对提高动态特性效果明显[9-11]。文献[12]设计了一种积分时变滑模变结构的速度环控制器，解决了传统PID控制器鲁棒性差、系统抗扰能力弱和动态响应性能不佳的问题。文献[13]对PMSM的无速度传感器控制进行研究，对滑模速度观测器进行了改进。为了减小延时并提高伺服系统电流环控制性能，文献[14]提出了一种基于无差拍控制原理的PMSM鲁棒预测电流控制算法。文献[15]为了增强系统的抗干扰性，提出了一种用于表面式PMSM的上下界滑模变结构速度控制方法。文献[16]提出一种扰动补偿控制方法。总之，以上方法具有较高的跟踪精度和鲁棒性，由于设计过程中没有对外部干扰进行估计，系统中参数微小变化或存在外部干扰时，系统的速度会存在一个较大的过冲，从而使得系统跟踪性能下降。

受以上文献启发，本文提出一种基于干扰观测器和滑模控制器相结合的PMSM速度控制方法。设计基于指数趋近律的滑模控制器，以提高电机系统的静态和动态跟踪性能。为了补偿负载干扰，进一步设计基于干扰观测器(以下简称DOB)的反馈控制特性。仿真与实验表明，本文的方法提高了PMSM控制系统速度跟踪精度，对负载干扰具有较好的抑制效果。

1 PMSM的数学模型及问题描述

为了简化分析，首先做如下假设：气隙中转子永磁磁场为正弦波；定子铁心不饱和，忽略涡流和磁滞损耗；转子上无阻尼绕组。在以上假设下，得到PMSM在d,q坐标系下的数学模型，其电压方程[3]：

(1)

式中：Ld,Lq分别为交、直轴电感；Rs为PMSM的定子电阻；ω为PMSM的角速度；ψf为交链磁链；uq,iq为PMSMq轴上的电压与电流分量；ud,id为PMSMd轴上的电压与电流分量。

PMSM的转矩方程：

(2)

式中：Te为PMSM的转矩；p为PMSM的极对数。对于隐极式PMSM,有Ld=Lq，因此可将PMSM的转矩方程简化：

(3)

PMSM的运动方程[3]：

(4)

式中：J,B分别为系统的转动惯量和摩擦系数；TL为系统的负载转矩。

将式(4)代入式(3)，可得：

(5)

式中：J=J0+ΔJ，TL=TL0+ΔTL，J0和TL0是系统参数的确定值，ΔJ和ΔTL表示系统参数的不确定性。

考虑到电机参数变化及未建模不确定性，式(5)可以进一步表示：

(6)

式中：Δa，Δb，Δc为系统参数不确定性摄动。

(7)

式中：d为不确定性干扰。

PMSM系统要求输出速度响应快、运行平稳，具有较高的速度跟踪精度。然而实际运用中，没有考虑外界干扰(如式(7)中的d)，会导致系统速度跟踪精度下降，从而影响PMSM控制系统性能。为了保证系统具有良好的稳定性和鲁棒性。本文提出一种基于DOB的滑模控制器，以提高PMSM控制系统的跟踪精度及外部干扰抑制能力。其控制系统结构框图如图1所示，图1中，ω*为给定转速，e为速度误差，SMC为滑模控制器。

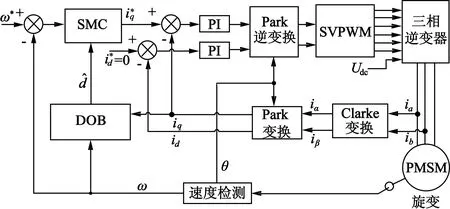
图1 基于DOB与SMC的结构框图

2 控制系统设计

2.1 滑模控制器设计

针对标称系统式(7)，即d=0，定义滑模面：

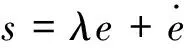
(8)

式中：λ为正常数。

对式(8)求导，可得：

(9)

趋近律函数采用指数趋近律：

(10)

式中：sat(·)为削弱抖振的饱和函数：

(11)

选取李雅普诺夫函数：

(12)

为抑制不确定的干扰，将DOB观测到的干扰估计引入控制器，由式(9)和式(10)，基于干扰补偿的滑模变结构控制律,q轴参考电流可设计：

(13)

对V2关于时间求导，根据式(9)有：

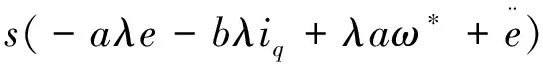
(14)

(15)

根据李雅普诺夫稳定性，闭环系统渐近稳定。因此在有限时间内，位置跟踪误差都将达到边界层。由式(8)和式(11)可知，速度跟踪误差的边界可以限定：

2.2 DOB的设计

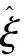
常见的DOB结构框图如图2所示。

图2 DOB结构控制框图

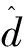
(16)

另外，由图2可以得出如下输入输出关系：

y=Gny(s)u+Gdy(s)D(s)

(17)

式中：

(18)

(19)

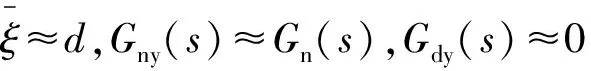
3 仿真与实验结果

3.1 仿真结果

为验证PMSM控制系统中，基于DOB的滑模控制器(DOB-SMC)的有效性，应用MATLAB/Simulink软件进行了仿真。PMSM的主要参数如表1所示；控制系统其他参数：摩擦系数B=0.008 N·m·s/rad，转动惯量J=0.000 35 kg·m2；控制器参数设置：λ=2 000，k=150，ε=500。

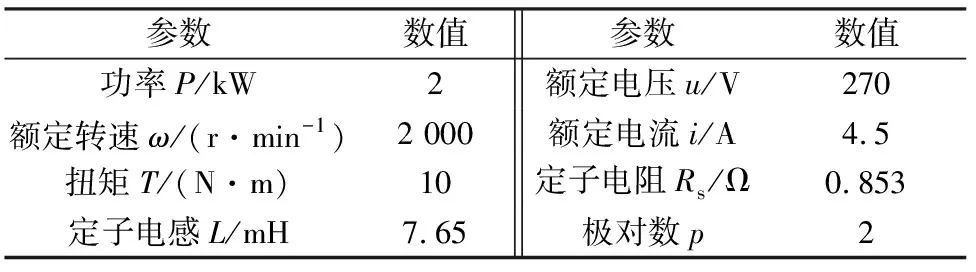
表1 永磁同步电动机参数

上述PMSM系统简化后得到速度环名义模型传递函数[17]：

(20)

为满足DOB设计条件，本文采用3阶低通滤波器[18]：

(21)

式中：τ为时间常数，决定Q(s)的截止频率。

初始给定转速为1 200 r/min，在0.6 s时给定速度为1 000 r/min，在0.8 s，加入了一个负载干扰。图3给出了SMC与DOB-SMC的速度响应波形。实线和虚线分别为采用SMC与DOB-SMC的速度跟踪曲线，由图3可以看出，SMC与DOB-SMC电机的转速跟踪性能良好，但当有负载或干扰时，DOB-SMC比SMC更快地达到稳定，且过冲更小。因此，DOB-SMC的干扰抑制效果明显。

图4为SMC与DOB-SMC的电磁转矩响应波形。图5,图6分别为SMC与DOB-SMC的三相电流波形。当速度瞬间变化时，三相电流会有尖峰，对应的转矩与电流成正比。

图3 SMC与DOB-SMC的速度响应

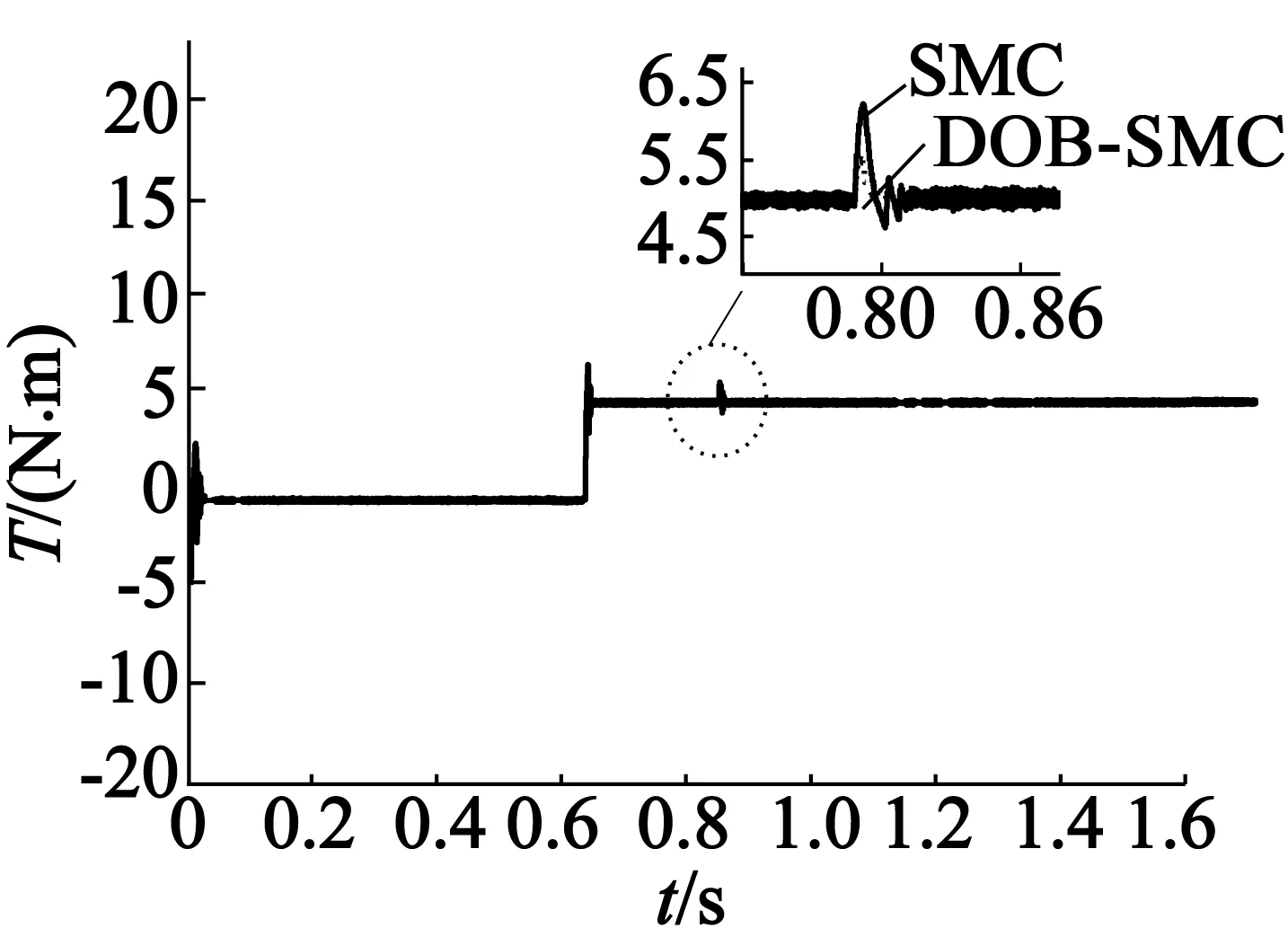
图4 SMC与DOB-SMC的电磁转矩响应

图5 SMC的三相电流波形

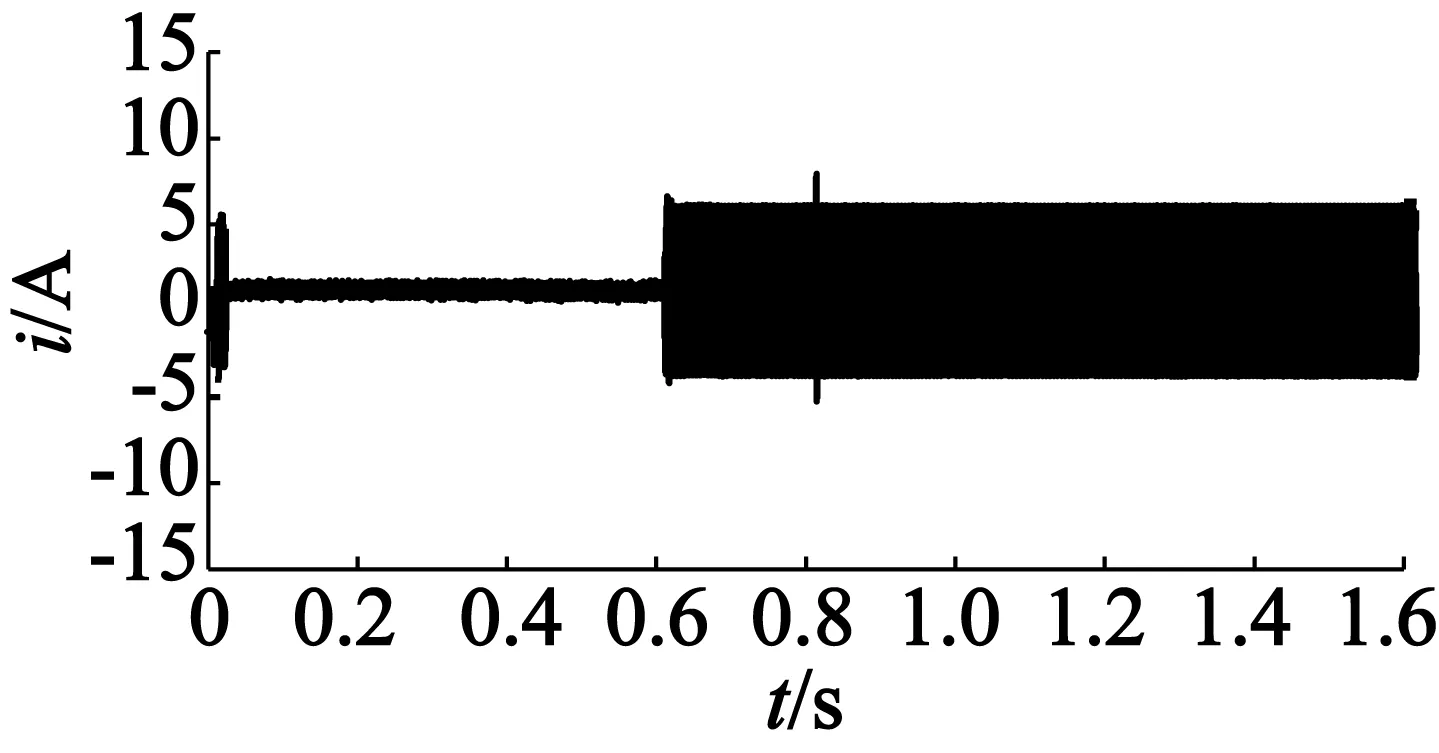
图6 DOB-SMC的三相电流波形

综上所述，本文的速度跟踪控制方法，能及时跟踪电磁转矩和给定的转速，使系统具有响应快，超调小，抑制负载干扰强等优点。

3.2 实验结果

PMSM实验平台如图7所示，平台中有2台PMSM，其中1台PMSM工作在电动状态，另1台PMSM工作在发电状态来模拟负载，负载大小由上位机软件调节，电机参数如表1所示。采用TI公司的DSP处理器TMS320F28035，功率器件采用英飞凌智能模块IPM。需要观测的数据可以通过软件设置在DSP主控板的模拟输出。

图7 永磁同步电动机实验平台

电机初始速度为0，从0.25 s开始均匀增速，到0.9 s时速度达到1 200 r/min，负载为0。图8、图9分别为SMC和DOB-SMC的实验波形。由图8的速度跟踪误差曲线可以看出，传统SMC的速度跟踪误差从0.25～0.5 s时间内速度存在误差，速度误差幅度最大达到40 r/min。由图9的DOB-SMC速度跟踪误差曲线可以看出，从0.2～0.35 s时间内速度也存在误差，速度误差幅度最大达到20 r/min。图10(b)中DOB-SMC的q轴参考电流波形，明显比图10(a)中传统SMC的电流波形平滑。

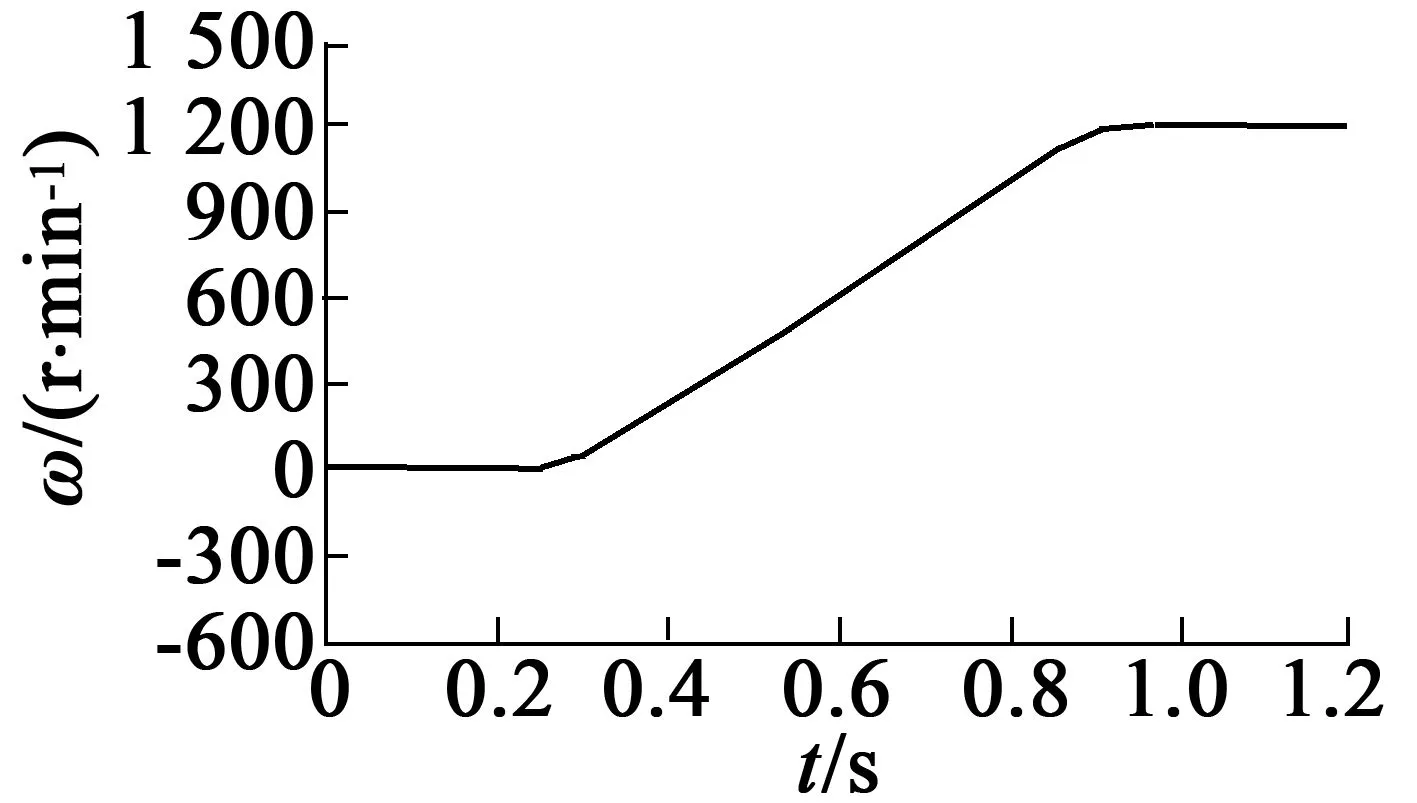
(a) SMC

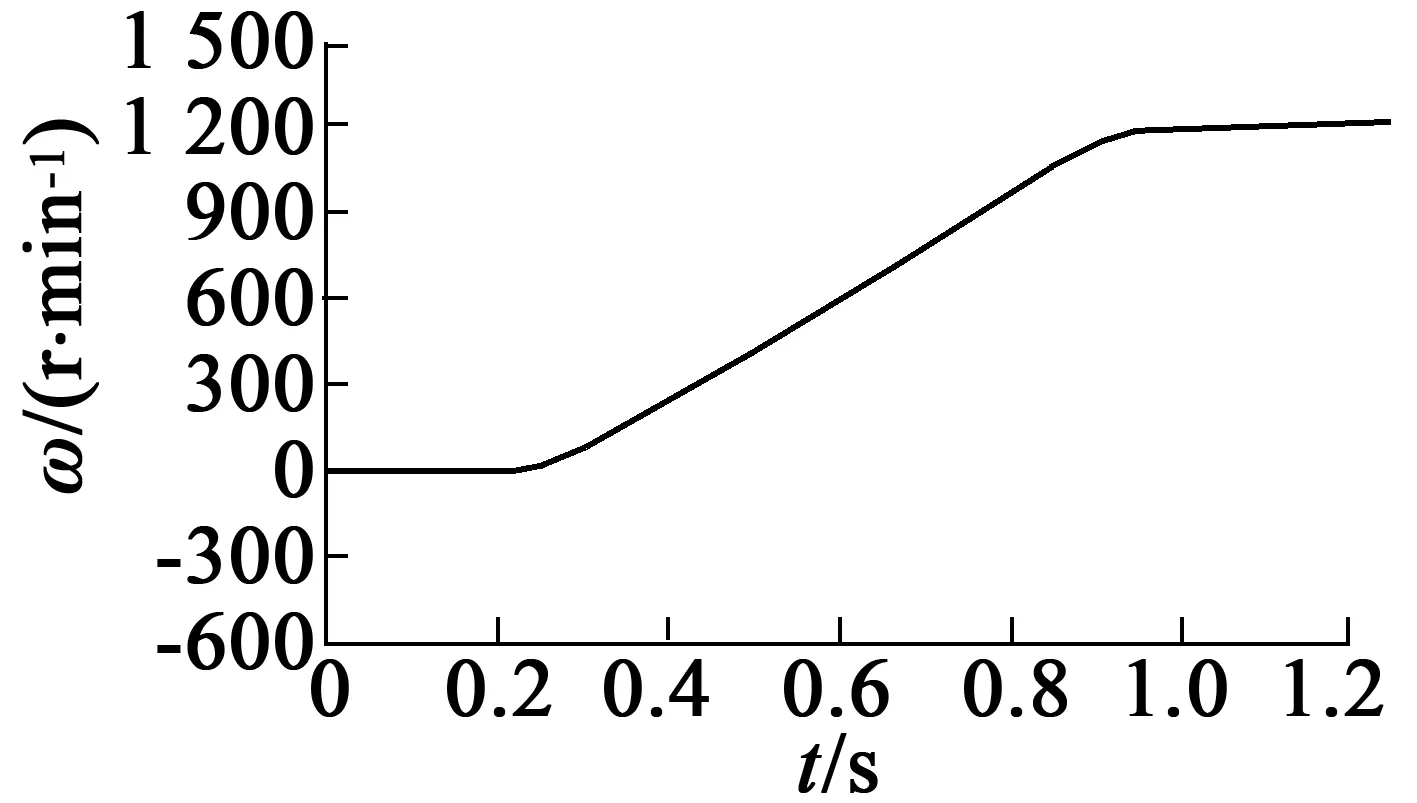
(b) DOB-SMC

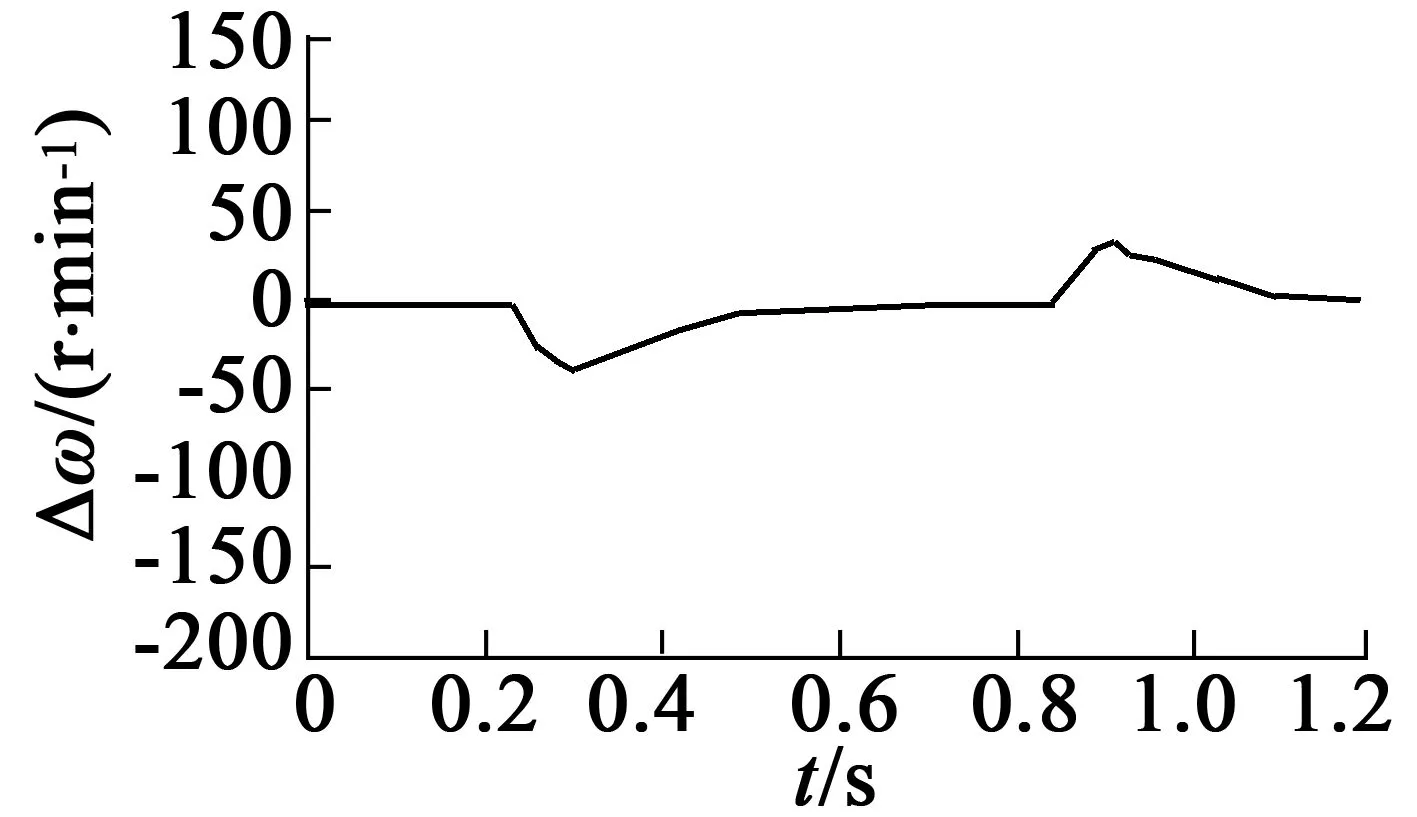
(a) SMC

(b) DOB-SMC

(a) SMC

(b) DOB-SMC

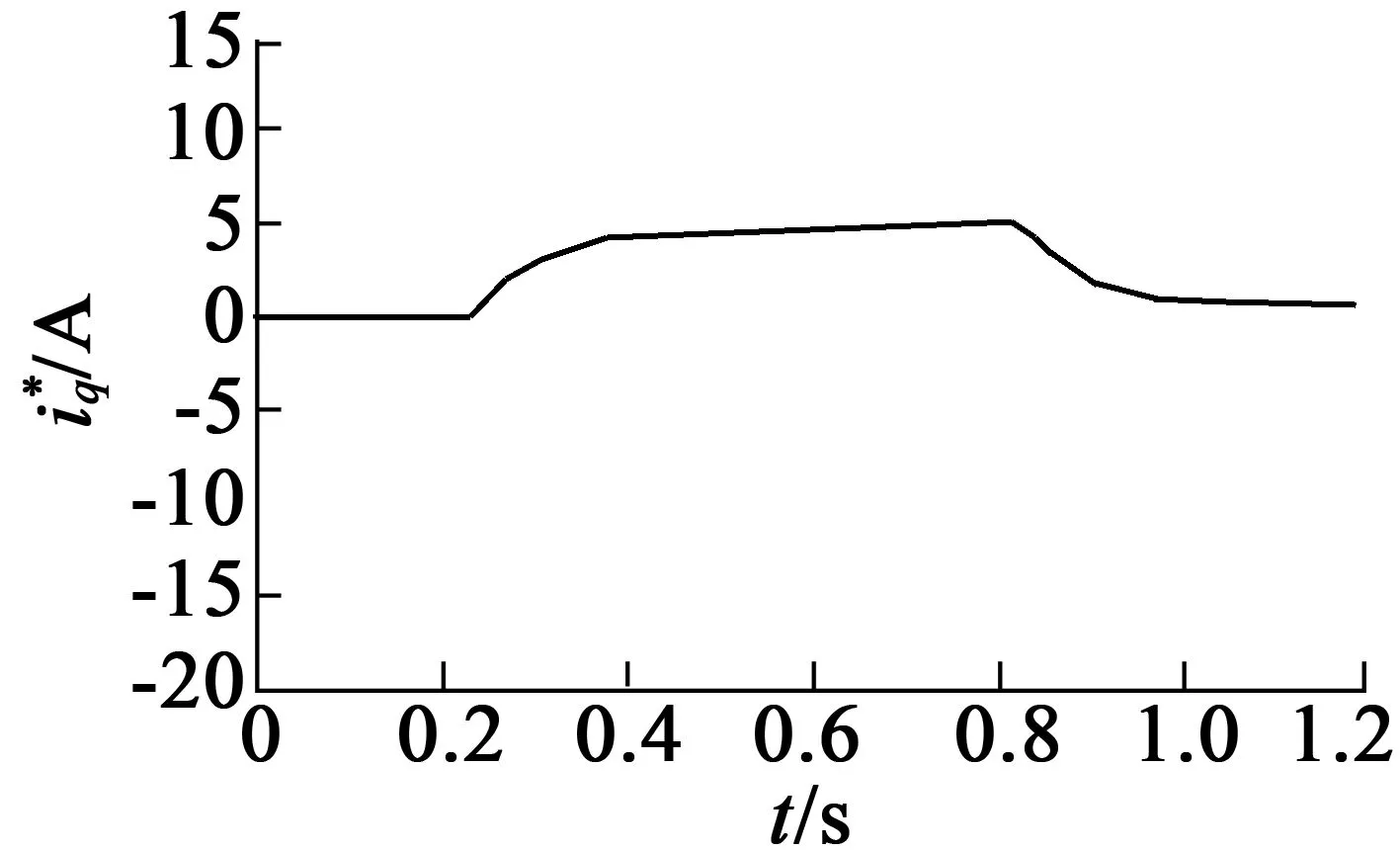
电机初始速度为1 000 r/min，负载为5 N·m，在0.25 s时将负载转矩增加至10 N·m，传统SMC与DOB-SMC速度响应与控制器输出的q轴参考电流分别如图11、图12所示。图11(a)中，在0.25 s时，负载转矩增加到10 N·m时，传统SMC速度最低为860 r/min，在0.48 s时达到稳定，调节时间为0.23 s;图12(a)为传统SMC输出的q轴参考电流，最大为5 A。由图11(b)为基于DOB-SMC速度最低为880 r/min，在0.35 s时达到稳定，调节时间为0.1 s，图12(b)为基于DOB-SMC输出的q轴参考电流，最大为4.8 A。由此可得出，本文的方法控制效果明显，具有较高的跟踪精度和响应速度。

(a) SMC

(b) DOB-SMC

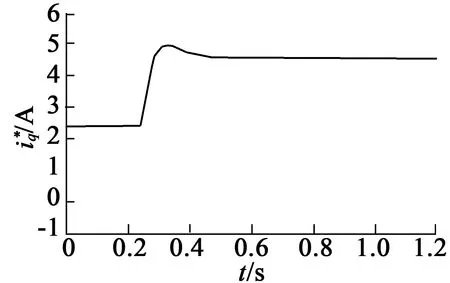
(a) SMC

(b) DOB-SMC

4 结 语

本文采用滑模变结构控制与DOB相结合的控制方法，利用基于指数趋近律的SMC,进一步提高电机系统静态和动态跟踪性能，通过基于DOB的反馈控制器来补偿负载干扰，提高系统的快速响应性，从而使PMSM控制系统具有更好的鲁棒性。仿真与实验结果表明，本文的方法与普通的滑模变结构控制相比，速度达到稳定的时间缩小一半，并且速度的过冲幅度进一步减小。因此本文的方法具有较高的跟踪精度和响应速度，对参数变化和外部扰动的鲁棒性强,具有较高的综合控制性能。