永磁同步电动机全阶状态观测器的设计及分析
赵武玲,魏 振,姚 广
(核工业理化工程研究院,天津 300180)
0 引 言
在永磁同步电动机(以下简称PMSM)矢量控制技术中,最为关键的是电机磁链位置的确定,一般会通过采用光电编码器等机械式位置传感器方式获得。但是对于某些控制精度要求不高、同时机械式位置传感器安装位置受限等应用场合,可以采用无位置传感器方式进行电机矢量控制[1-4]。目前,常见的无传感器控制方法主要有模型参考自适应估算法、基于人工智能理论的估算法、滑模观测器估算法及磁链观测器估算法等,其中滑模观测器以其具有鲁棒性强、系统响应迅速、易于工程实现等优点,成为目前应用较多的估算方法。但是传统的二阶滑模观测器作为一种典型算法,其切换函数为开关函数,具有抖振问题,容易造成系统性能变差甚至不稳定,实际应用中大多会采用改进的开关函数即饱和函数,从而消除滑模观测器固有的抖振现象。采用饱和函数的滑模观测器实际上是一种准滑模观测器,在边界层外是非线性的开关控制,在边界层内是线性控制,尤其是一旦边界层选取的范围很大,滑模控制基本上等价于线性控制。但是滑模观测器的稳定性分析大多建立在非线性开关函数基础上[5-7],对连续函数部分的稳定性分析很少,而且进一步分析会发现采用线性函数的观测器状态方程还会耦合感应电动势的影响。
因此本文从线性控制的角度出发,采用全阶状态观测器方法,重点分析了系统的稳定性问题,推导出状态观测器反馈增益系数的取值范围,同时通过全阶状态方程可以直接得到反电动势的表达式,从而得到转子位置及转速,无需低通滤波器环节,避免了相位延迟的影响。最后搭建了电机实验平台并进行实验,实验结果验证了采用全阶状态观测器的可行性及其反馈增益系数取值范围的有效性。
1 PMSM数学模型
PMSM(表贴式)在两相静止坐标系下的数学模型可以表述:
(1)
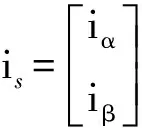
由eα,eβ,求得PMSM转子位置及速度:
(2)
一般而言,电机转速的变化要远远小于电机电流的变化,因此在很小时间范围内,可认为电机角速度为恒定值,电机反电动势模型可表述:
(3)
以同步电机定子电流及反电动势作为状态变量,由式(1)、式(3)可建立电机扩展反电动势的全阶状态方程,表达式如下:
(4)
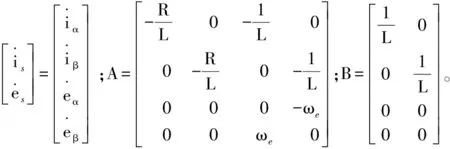
2 PMSM全阶状态观测器设计
2.1 PMSM全阶状态观测器的建立
设计PMSM全阶状态观测器,目的是为了得到电机反电动势,获取电机磁场的磁链信息,从而实现PMSM矢量控制。以PMSM全阶状态方程表达式(4),作为参考模型,按照状态观测器的基本原理,构造出一个与之类似的模拟被控系统,来模拟电机实际运行。其状态方程:
(5)
式中:x*为电机状态向量的估算值(电机定子电流is,电机反电动势es)。由于电机定子电流通过电流传感器检测到可作为电机输出向量,因此y*即为电机输出向量is的估算值。理想状态下,希望模拟系统与参考模型二者无限逼近。但实际应用中,模拟系统状态向量很难被检测到,尤其是电机反电动势,而系统状态向量的变化却会直接反映到输出向量的变化;同时由于电机定子电流的可检测性,于是根据一般反馈控制原理,将输出向量的误差负反馈至状态向量处,使模拟系统快速逼近参考模型,从而得到电机反电动势的观测值,用于电机矢量控制。状态观测器结构图如图1所示[8]。
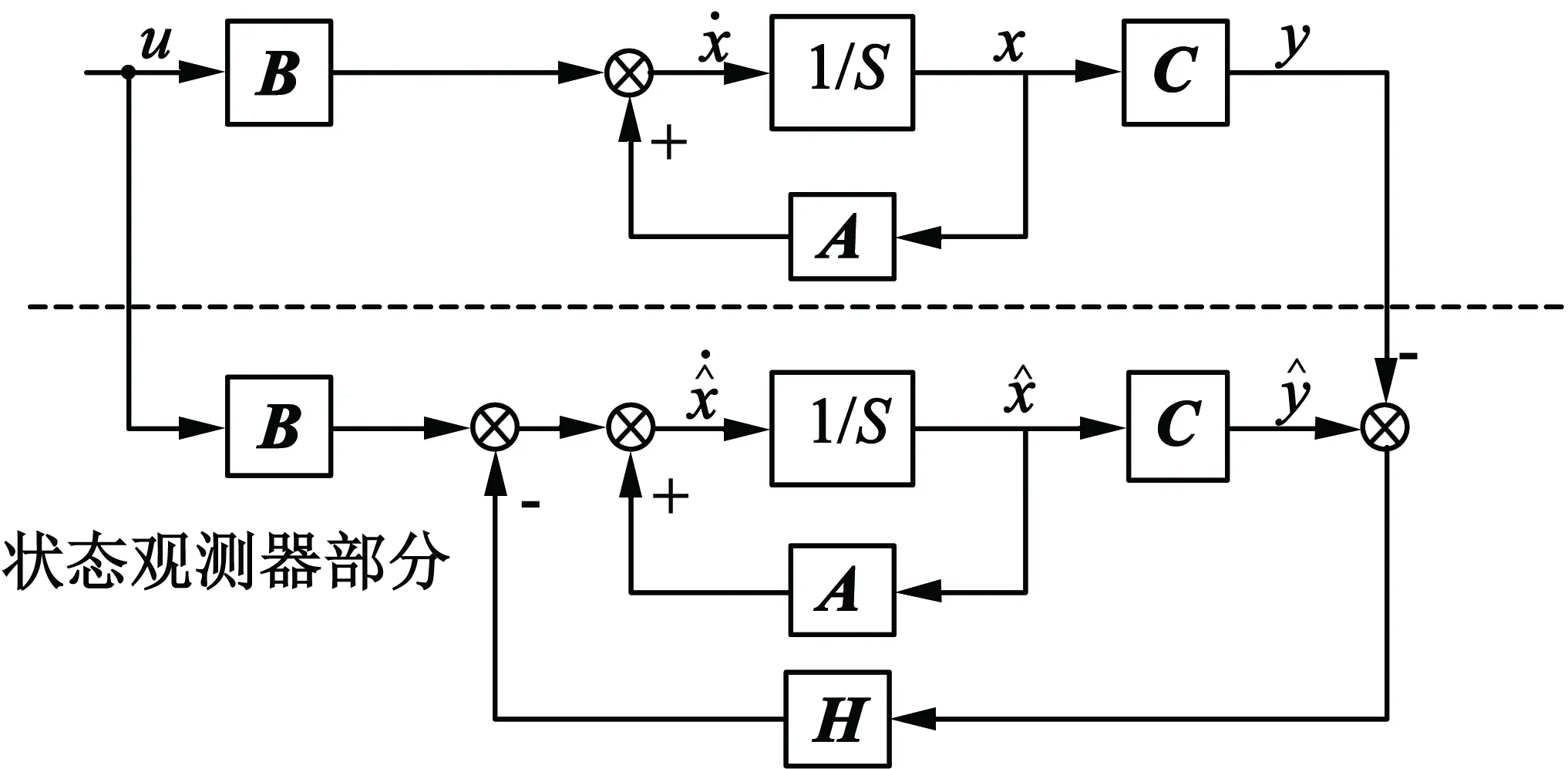
图1 状态观测器结构图
根据上述状态观测器的原理,取电机定子电流is、反电动势es为状态变量,定子电流is可通过电流传感器测量得到作为状态方程的输出量,反馈控制函数H可选择滑模控制或线性反馈控制等多种控制方式,尤其是滑模控制,为了改善其抖振效应,多采用饱和的准滑模控制。但是经过分析,可以看出准滑模控制在滑模面的边界层外是滑模控制,而线性区内实际是一种线性控制方式,尤其是当滑模边界层范围比较大时,其基本上等价于线性控制,因此本文结合准滑模控制理论直接采用线性反馈控制策略,同时简化反馈矩阵,得到了PMSM的全阶状态观测器,表达式如下:
(6)
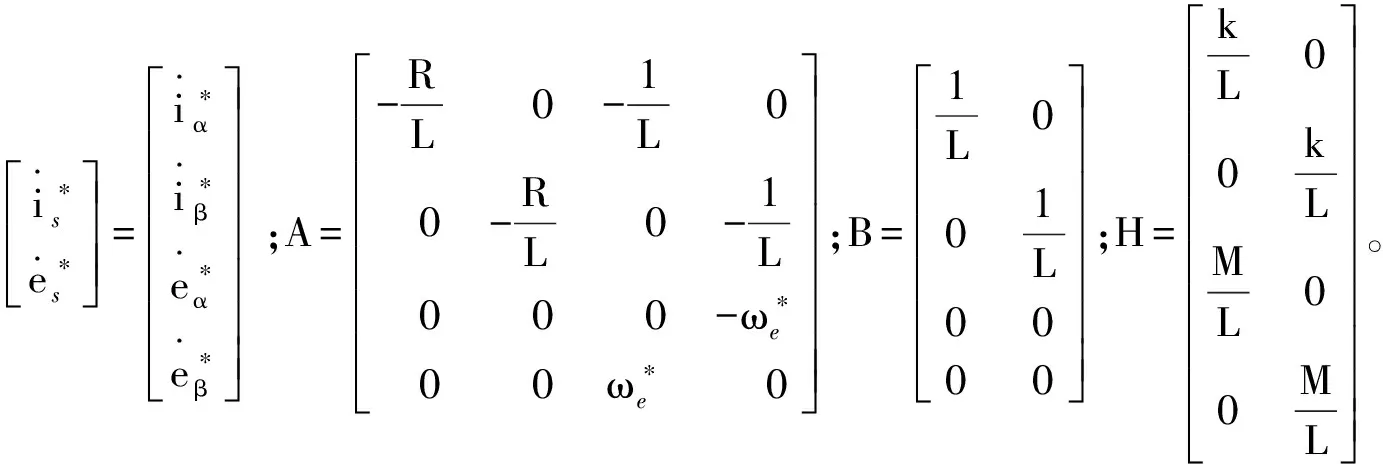
2.2 稳定性分析
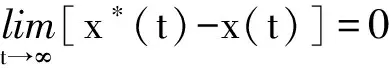
(7)
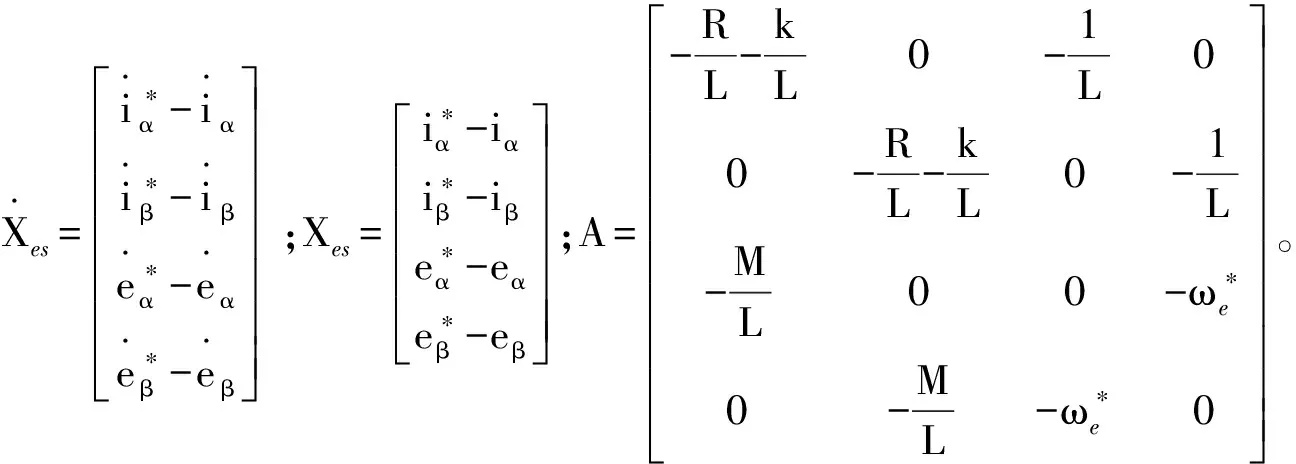
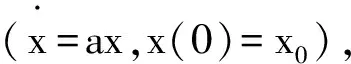
(8)
经过推导,最终可以得到特征方程:
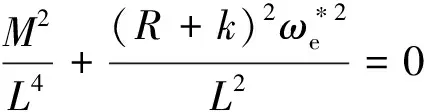
(9)
根据李雅普诺夫第一法,只要式(9)的特征值均具有负实部,则系统稳定。因此,为了保证系统的渐近稳定性,按照四阶线性系统赫尔维茨稳定性判据,特征方程的各项系数(a0,a1,a2,a3,a4)为正,得到:
(10)
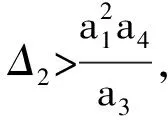
(11)
经过推导,得到M,k的取值范围:
(12)
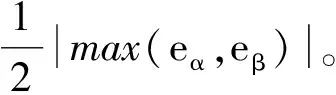
2.3 反电动势的离散化提取
在实际应用中,为了便于程序化实现,对式(7)进行离散化,从而得到估算电流、估算反电动势表达式:
(13)
3 基于全阶状态观测器的PMSM矢量控制系统
3.1 控制系统设计
PMSM矢量控制系统如图2所示。系统主回路采用交直交变换方式,由整流器、三相逆变器构成。整流器采用二极管不控整流方式,三相逆变桥IGBT组件选用德国赛米控公司SKM200GB12V。系统控制电路以TI公司电机控制套件专用芯片TMS320LF28335为核心,完成直流电压采集、电机电流采集、电压采集、控制算法实现、SVPWM算法及初始相位调零等功能。三相定子绕组电流通过霍尔电流传感器采样得到,直流电压、线电压直接通过控制板差分电路变换得到。所有控制算法全部通过DSP实现,逆变器开关频率选取10 kHz,采样周期设定为100 μs。
实验选用MOTEC有限公司生产的PMSM,其型号为SEM-190C110303HN。电机主要参数如下:额定输出功率11 kW,额定相电流20 A,额定转速3 000 rad/min,电机转矩35.8 N·m,电机磁极对数为4,定子电阻R为2.3 Ω,定子电感L为0. 96 mH。
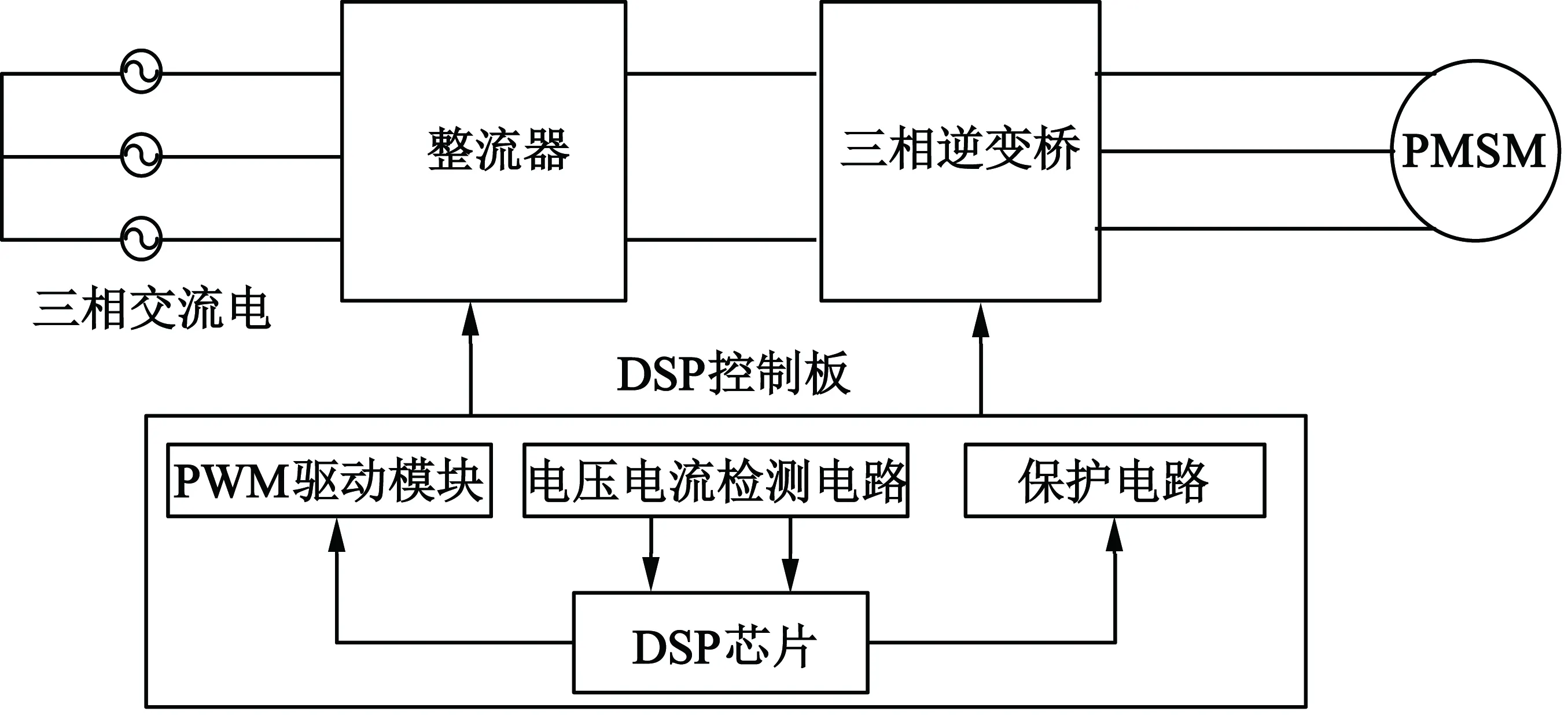
图2 PMSM控制系统硬件结构框图
3.2 控制过程
本文的全阶状态观测器算法无法实现电机的零速起动,因此整个电机起动运行采用先调零、再恒流升速、最后转速环电流环双闭环运行的方式。
控制器接收起动指令后,采用给电机定子通过一个已知大小、方向的直流电方法进行转子预定位,这个直流电产生的恒定磁场与电机转子磁场相作用,从而迫使转子转到该直流电对应的磁场位置,完成转子位置的初始化[11]。本文采用通以id=idref,θ=0的直流电流磁场定位方法进行PMSM调零,实现转子位置的初始化。
电机准确调零定位后,采用恒流方式同步拖动电机并加速旋转,加速至一定转速后,再通过缓慢降电流方式切入转速、电流双闭环控制模式,实现电机转速控制。
3.3 实验及结果分析
根据前述控制过程,本文采用全阶状态观测器方法,电机首先进行调零,再以恒电流(5 A)方式拖动电机转速升至300 r/min,执行切换程序,转换至转速电流双闭环控制模式运行直至达到额定转速3 000 r/min。全阶状态观测器反馈增益系数选取为k=0.2,M=-5。整个过程起动运行过程,电机运行正常,切换平稳。
实验进行全阶状态观测器与文献[4]传统二阶滑模观测器算法对比,二者实验平台采用单电机实验,硬件平台完全一致,仅电机转子磁场位置检测算法不同。电机首先采用滑模观测器方法起动运行,同时计算监测全阶状态观测器估算的角度。其中滑模观测器控制函数采用饱和函数,为抑制谐波,对反电动势信号进行低通滤波,滤波器截止频率随着目标频率变化,采用3倍于参考转速方法,为观测实验效果,未进行相位补偿。
图3为滑模观测器与全阶状态观测器估算角度对比图,电机转速3 000 r/min,所测波形为经过观测器算法计算得到的转子位置数据。其中图3(a)为滑模观测器估算角度波形,图3(b)为全阶状态观测器估算角度波形,电机转速运行周期约为5 ms,二者相位相差约12°,约接近于理论计算值。二者估算角度趋势基本保持一致,光滑度基本保持一致。
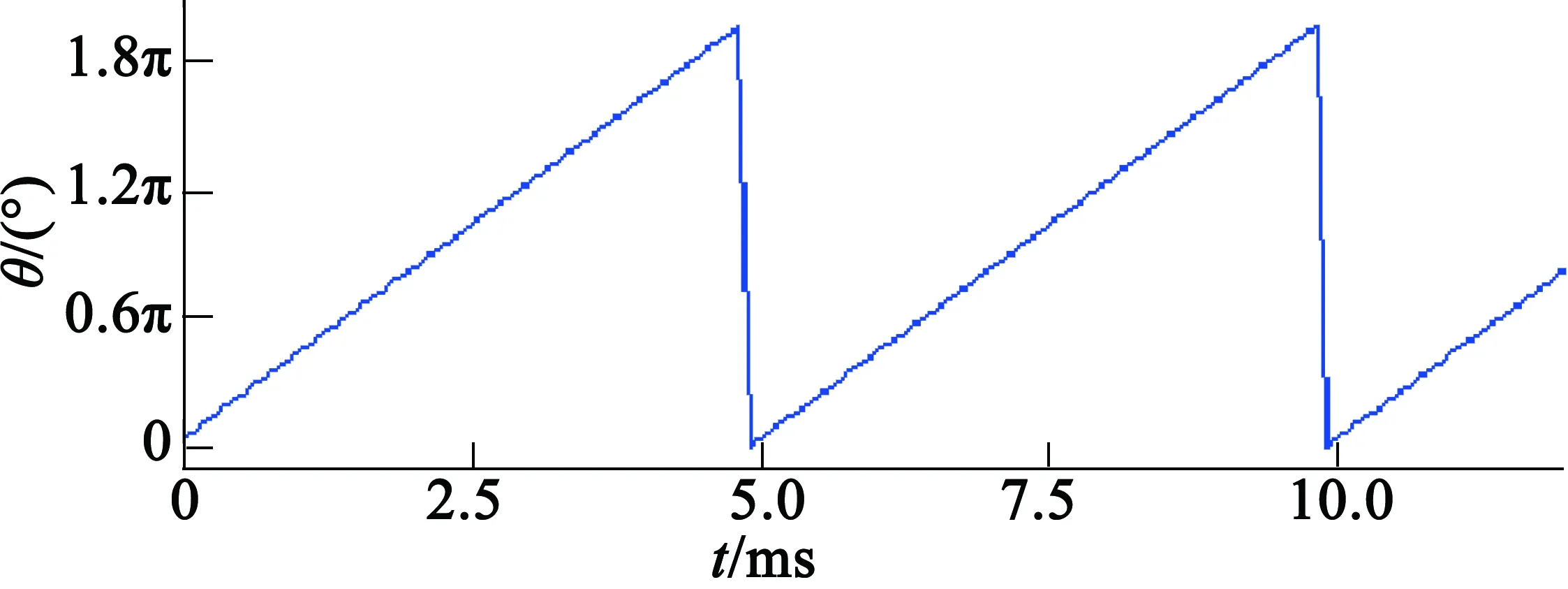
(a) 传统滑模观测器所测转子位置
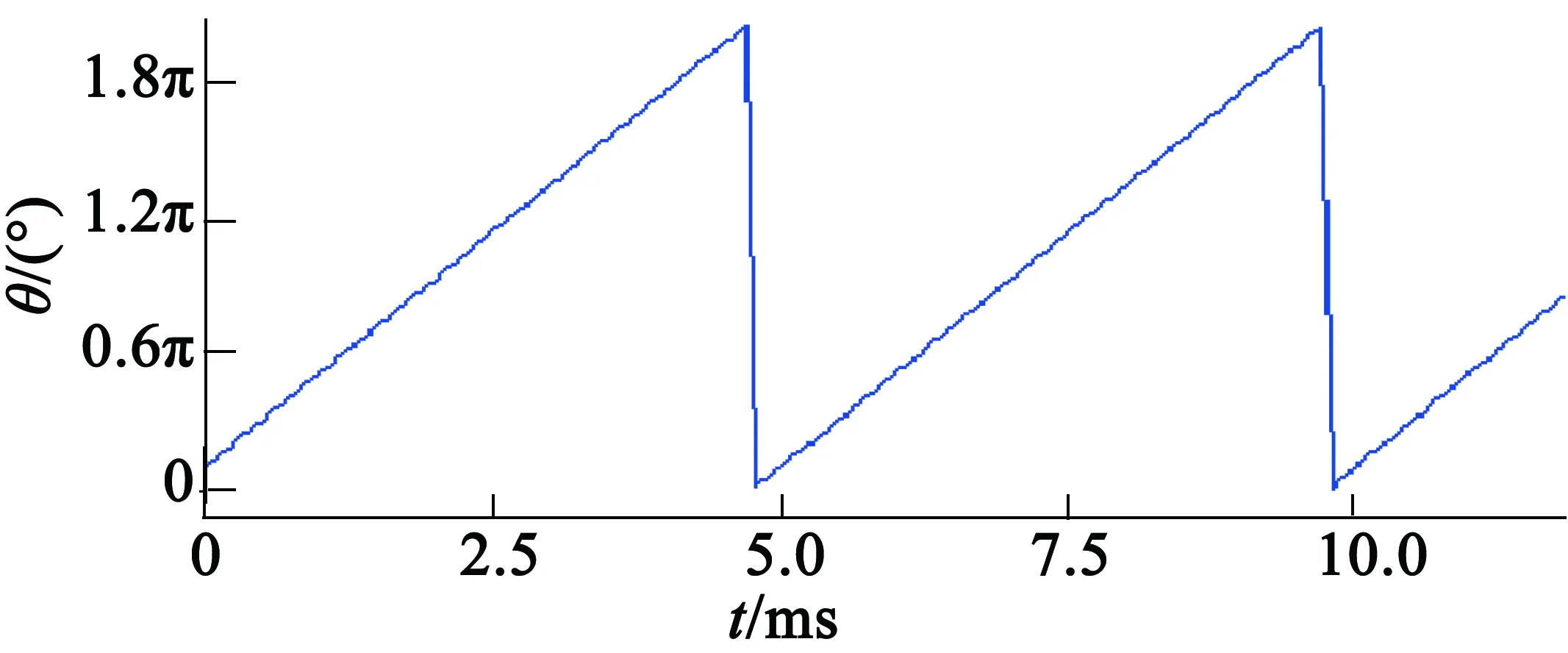
(b) 全阶状态观测器所测转子位置
图4为电机转速为3 000 r/min时的定子电流波形图,空载时电机定子电流有效值约为2 A,其中图4(a)为实测定子电流波形,通过电流传感器实测电流值经过DSP的AD采集口输出数据,图4(b)为全阶状态观测器估算电流波形图。由图4可知,全阶状态观测器估算电流波形基本接近于实测电流波形,估算电流幅值与真实值基本一致。
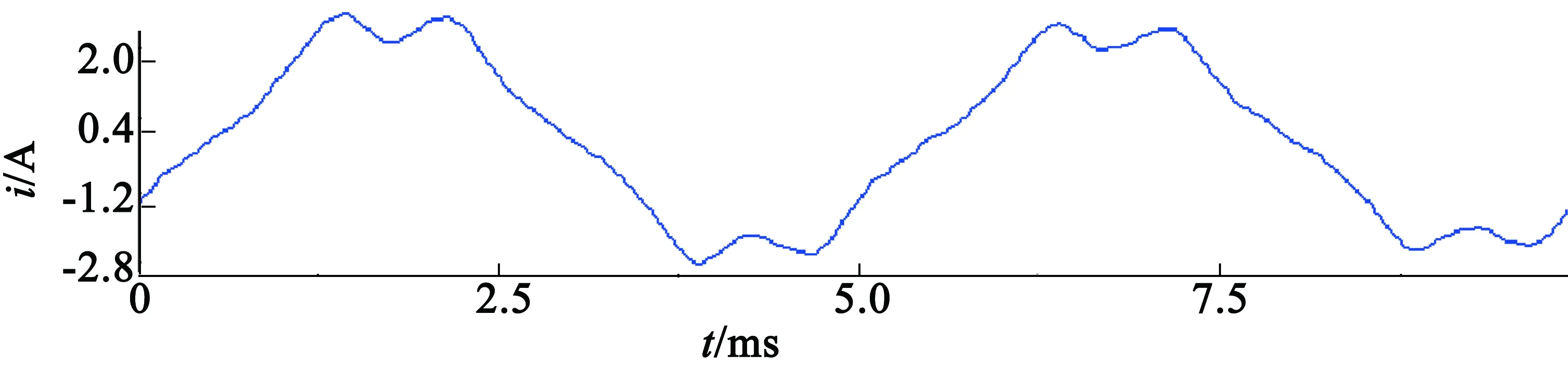
(a) 实测定子电流
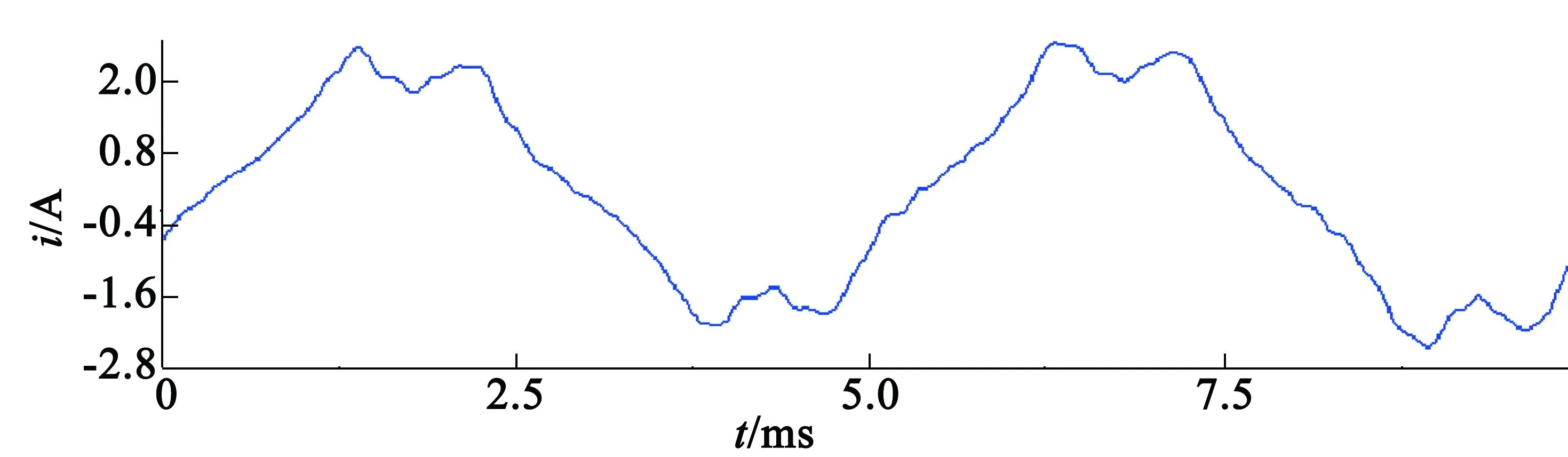
(b) 全阶状态观测器估算定子电流
4 结 语
本文从线性控制的角度出发,研究了一种全阶状态观测器估算方法,直接得到估算反电动势的表达式,从而得到转子位置及转速。本文重点分析了全阶状态观测器系统的稳定性问题,推导出满足系统收敛性的反馈增益系数的取值范围。最后为了验证全阶状态观测器估算方法的可行性和有效性,搭建了永磁同步电动机实验平台,进行了相关实验。实验结果表明,通过全阶状态观测器直接得到反电动势估算值,从而得到估算角度值,具有良好的效果,减少了传统滑模观测器低通滤波器环节,算法简单,而且在电机起动运行全过程中动态调整性能与滑模观测器基本保持一致,实验结果验证了全阶状态观测器算法的可行性及其反馈增益系数取值范围的有效性。

