两极平行充磁环形永磁体磁场解析计算

张岩岩，周 健，耿海鹏，徐祥铭，程文杰，虞 烈

(1.西安交通大学，西安 710049； 2.西安科技大学，西安 710054)

0 引 言

弹性箔片轴承支承的高速永磁同步电机主要应用于燃料电池空气压缩机、微型燃气轮机等各种透平机械中，高转速、大功率密度、特殊支承等特点使其在设计制造、研究分析、实验测试等方面都不同于普通电机，也使得对其进行深入研究以提高设计技术显得尤为重要。电磁场分析是电机研究中的基础和重点内容，磁场分布计算和分析的结果是设计、优化电机电磁性能的关键，影响着电磁转矩、电磁振动和噪声、电磁损耗等电机特性计算的准确程度，还直接影响着电机的控制性能。

对于永磁电机永磁体转子励磁磁场分布的计算，目前主要采用有限元法和解析法。有限元法计算精度高，能够处理结构比较复杂的电机模型，但是建模和计算要消耗一定的时间量；解析法计算量小，方便简单，速度也快，但是针对复杂结构的电机，励磁磁场解析表达式的推导似乎有些困难。针对多极表贴式永磁电机，Boules在1984年给出了直角坐标系下永磁无刷同步电机磁场的二维解析解[1]，该模型考虑了永磁体的漏磁、永磁体磁动势沿高度的分布以及永磁体宽度的变化(由于永磁体弧角不变)，利用卡特系数和饱和因子分别考虑定子开槽效应和磁路中铁心的饱和效应。1985年Boules提出用等效载流线圈代替永磁体的励磁作用[2]，并在极坐标系下建立了永磁无刷同步电机和永磁直流电机径向充磁和平行充磁时定、转子铁心表面空载磁场分布的解析模型。Gu等推导了表贴式永磁电机永磁体励磁磁场的解析解[3]。1993年Zhu等建立了更为通用的开路磁场分布的求解方法[4]，这种方法在极坐标系下通过求解拉普拉斯方程(气隙区域)和泊松方程(永磁体区域)获得开路磁场的解析解。尽管这种方法针对的是永磁无刷直流电机，但对于无刷永磁交流电机、永磁有刷电机也是适用的。王兴华等[5]利用定解条件，求解关于标量磁位的偏微分方程，得到永磁无刷直流电机径向永磁磁场的解析表达式。对于形状简单磁化均匀的永磁体，2007年文献[6]引入磁荷密度和圆环谐波函数，推导了平行充磁的两极实心圆柱永磁体置于空气中时励磁磁场的三维解析解，但是文献没有考虑当永磁体置于定子腔中的情形。Rahideh 等[7]推导了外转子和内转子无槽无刷表贴式永磁电机6种磁化方式下开路磁场分布的解析表达式，在模型建立的过程中，定、转子铁心被视为具有有限值的磁导率。李界华等[8]推导了径向充磁和两段式Halbach充磁两种充磁方式下永磁电机空载气隙磁密的解析解。黄克峰等[9]利用面电流等效永磁体，推导了径向充磁表贴式永磁同步电机空载时定子内表面磁场的解析表达式。

很多关于永磁电机永磁体磁场解析计算的文献主要是针对极弧系数小于1的瓦片形磁极，对于这种磁极，径向充磁和平行充磁下，将磁化强度M表达成傅里叶级数的形式后都有×M≠0或divM≠0。由于常规的叠片转子难以承受高速旋转产生的离心力，高速或超高速永磁同步电机普遍采用实心转子，即永磁体采用实心圆柱式或内装心轴的圆环形，这些结构类型的永磁体，与极弧系数等于1的瓦片形永磁体相同，平行充磁下却有×M=0或divM=0，因此现有的很多文献中的解析模型不再适用。由于高速或超高速永磁同步电机设计中的理论需要，获得这类永磁磁场解析计算公式显得特别重要。文献[10]针对内装导磁铁心的2极平行充磁磁环(或2片180°磁瓦)，给出了气隙中开路静磁场径向分量的解析计算公式，指出该磁场是正弦分布的。但是当永磁体内侧存在二次气隙时，文献[10]给出的解析表达式不再适用，在此情况下，文献[11]在文献[10]的基础上推导了更为通用的解析计算公式，并将该公式扩展到铁心或心轴采用不导磁材料以及转子置于空气中的情形，但也只给出了磁场径向分量的表达式。2015年Cheng等[12]给出了极坐标系下平行充磁实心圆柱式永磁体(以下简称SCPM)和内装导磁心轴的环形永磁体(以下简称RSPM)置于定子腔以及空气中时产生的磁场的二维解析模型，结果显示,4种情形下各向磁场均为正弦分布。可见，目前仍然缺少可以计算内装不导磁心轴的平行充磁RSPM各向磁场分布的解析公式，本文以此类永磁体为研究对象，就其置于定子腔(情形1)以及空气中(情形2)进行磁场分布精确解析计算模型的推导和有限元验证，为采用这类结构的平行充磁高速永磁同步电机的优化设计、性能分析以及转子永磁体充磁后的磁场检测提供有用、可靠的理论依据，也为继续计算和分析这类电机电磁振动和噪声、电磁损耗等相关特性提供条件和便利。

1 永磁体磁场的解析模型

1.1 永磁转子置于定子腔中

1.1.1 数学模型

图1为内装不导磁心轴的两极平行充磁环形永磁同步电机(以下简称RSPMSM)的基本模型。图1中，Rs为定子内半径，Rp为永磁体外半径，Rf为心轴外半径。这种结构类型电机的转子永磁体外面一般

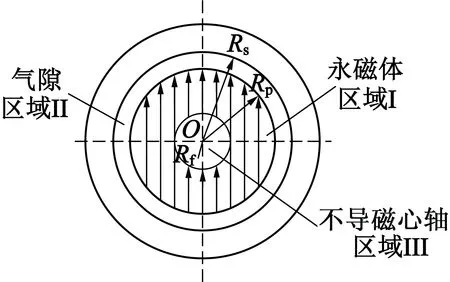
图1 电机分析模型

增加保护套，由于保护套选用不导磁合金，相对磁导率与空气近似，在计算静磁场时将保护套和不导磁心轴同时作为空气处理。根据材料和结构特点，将整个求解场域划分为永磁体区域Ⅰ、气隙区域Ⅱ和不导磁心轴区域Ⅲ3个子域，在极坐标系下建立数学模型，下角标r，θ和z分别表示变量的径向、周向和轴向分量。为了简化求解，作如下假设：

(1)不考虑端部效应；

(2)忽略涡流效应和饱和效应；

(3)将定子铁心的相对磁导率视为无穷大；

(4)永磁体的退磁曲线是线性的。

1.1.2 磁化强度

如图2所示，对于平行充磁的永磁体，在极坐标系下，磁化强度M可以写为：

M=Mrr+Mθθ

(1)

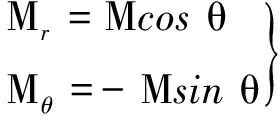
(2)

式中：M=|M|；Mr和Mθ分别为永磁体磁化强度的径向和周向分量。

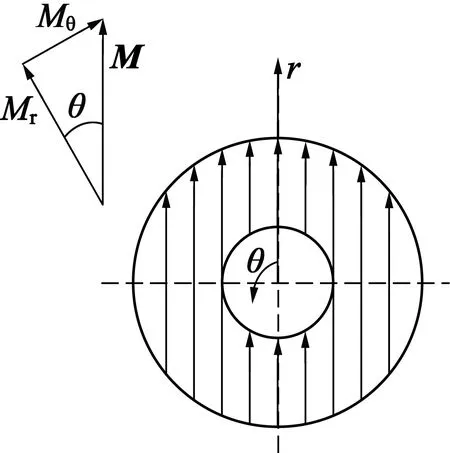
图2 两极平行充磁RSPM的磁化模型

1.1.3 矢量磁位通解

在永磁体区域Ⅰ，矢量磁位AⅠ满足泊松方程，在气隙区域Ⅱ和不导磁心轴区域Ⅲ，矢量磁位AⅡ和AⅢ满足拉普拉斯方程，即：

(3)

式中：μ0为真空磁导率，μ0=4π × 10-7H/m。

对于二维磁场，A=Azez，Ar= 0，Aθ= 0，因此3个区域的控制方程可以写为Az的二维泊松方程：

2Aiz=0 (i=Ⅰ,Ⅱ,Ⅲ)

(4)

式(4)可以用分离变量法求出如下通解：

式中：Ei0，Fi0，Li0，Mi0，Eim，Fim，Lim和Mim为待定系数。

磁通密度和矢量磁位的关系如下：

(6)

式中：Br和Bθ分别为磁通密度的径向和周向分量。

在各个区域内，磁感应强度B、磁场强度H和磁化强度M的关系可记为：

(7)

式中：μr为永磁体的相对磁导率。

根据磁场的对称性，有：

(8)

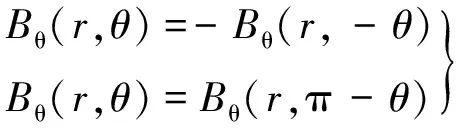
(9)

根据式(6)、式(8)和式(9)，可将式(5)简化成：

(10)

1.1.4 边界条件和接口条件

在定子内表面(r=Rs)有：

HⅡθ|r=Rs=0

(11)

式中：Hθ为磁场强度的周向分量。

在气隙区域和永磁体区域分界面(r=Rp)，径向磁密和周向磁场强度连续，因此有：

(12)

同样地，在永磁体区域和不导磁心轴区域分界面(r=Rf)，有：

(13)

由式(10)，结合式(6)、式(7)以及边界和接口条件式(11)、式(12)和式(13)，可以得到不同区域内各向磁场分布的解析计算公式。设定空间角θ= 0位于转子永磁体磁极的中心线上，在永磁体内，有：

(14)

在气隙区域中，有：

(15)

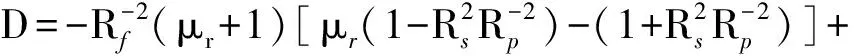
(16)

1.2 永磁转子置于空气中

与永磁转子置于定子腔中的情形类似，将求解场域分为永磁体区域Ⅰ、永磁体外部区域Ⅱ和不导磁心轴区域Ⅲ3个子域，如图3所示。

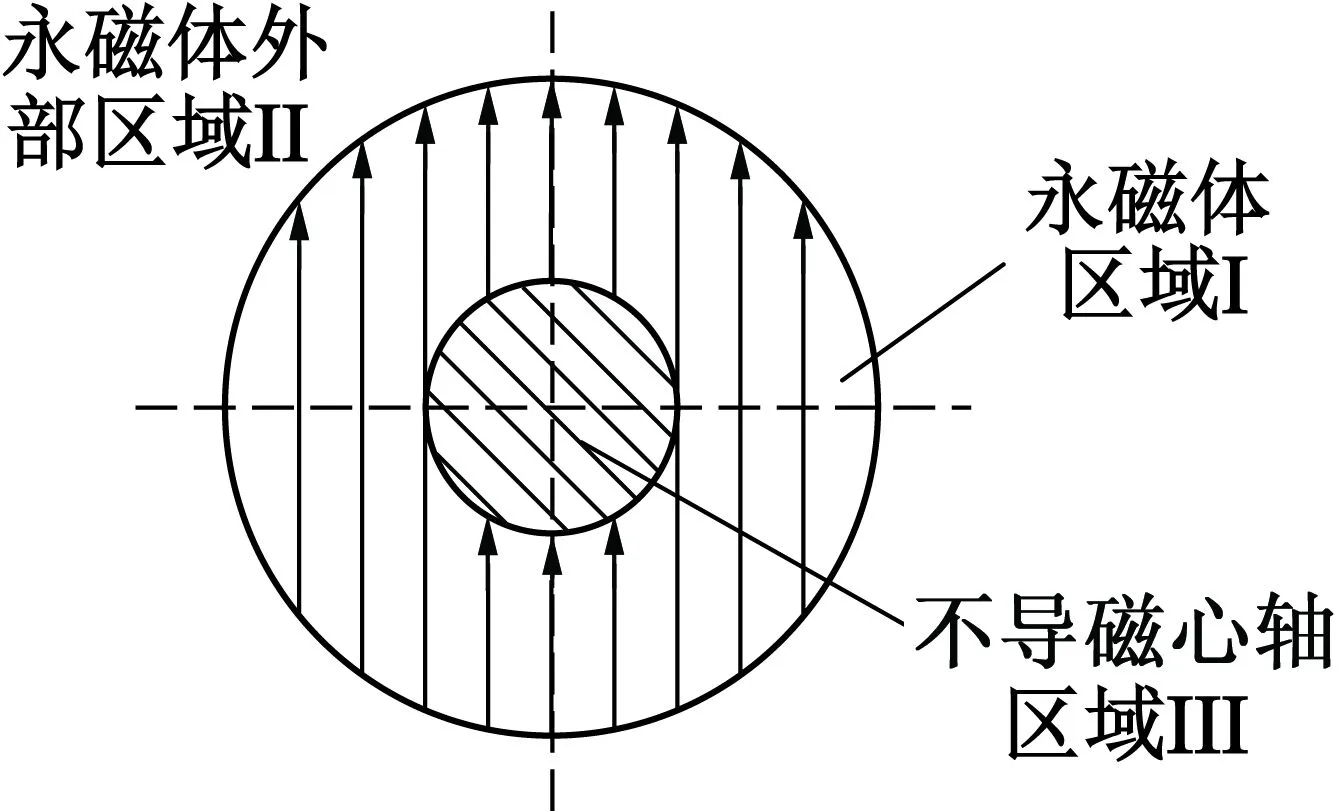
图3 电机的求解区域(情形2)

3个区域控制方程和矢量磁位通解的形式同式(4)和式(10)。

在永磁体外部区域无穷远处(r= ∞)应有：

HⅡr|r=∞=0，HⅡθ|r=∞=0

(17)

在永磁体外部区域和永磁体区域分界面(r=Rp)，接口条件的形式同式(12)。

在永磁体区域和不导磁心轴区域分界面(r=Rf)，接口条件的形式同式(13)。

由式(10)，结合式(6)、式(7)以及边界和接口条件式(17)、式(12)和式(13)，可以得到不同区域内各向磁场分布的解析计算公式。在永磁体内，有：

(18)

在永磁体外部空气中，有：

(19)

2 有限元仿真验证

以一台内装不导磁心轴的两极平行充磁RSPMSM为例，分析永磁体产生的磁场，样机相关参数如表1所示。本文解析模型没有考虑齿槽效应，为了考虑定子开槽对气隙磁场的影响，引入气隙相对比磁导函数[13]。

表1 样机相关参数

在电磁场分析软件Ansoft Maxwell中建立电机的有限元模型，进行开路静磁场的仿真计算，得到气隙区域和永磁体区域各向磁通密度分布，与本文解析模型计算结果的对比如图4所示。可以看出，对于内装不导磁心轴的两极平行充磁RSPM，当置于定子腔中时，磁通密度是标准的正弦波形，在一个机械周期内呈1个周期分布，与电机极对数相对应。永磁体内磁密波形的解析结果和有限元结果吻合得较好，距离定子内径较远处，定子齿槽对气隙磁密的影响较小，解析解和有限元解也能够较好地吻合。越靠近定子内径，定子开槽对气隙磁密的影响越大，齿槽效应使得气隙磁密在定子槽口处有波动，尤其是在距离磁极相对较近的槽口区域。另外，齿边缘区域气隙磁导的急剧变化而引起的聚磁效应使气隙磁密波形在齿边缘出现尖峰。解析模型是在定子内径光滑的假设下获得的，没有考虑齿槽效应，而气隙相对比磁导函数又无法考虑定子齿尖处的聚磁效应，因此靠近定子内径处，解析计算结果与有限元计算结果在齿尖处相差较大。对于气隙磁密的周向分量，由于聚磁效应，其波形在齿尖处出现锯齿状，同时还可以看出，气隙相对比磁导函数不能反映定子开槽对气隙磁密周向分量的影响。

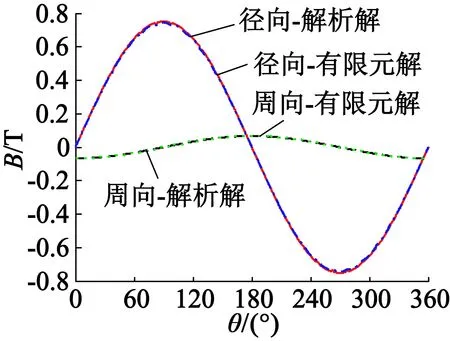
(a) 气隙区域(r= 43 mm)

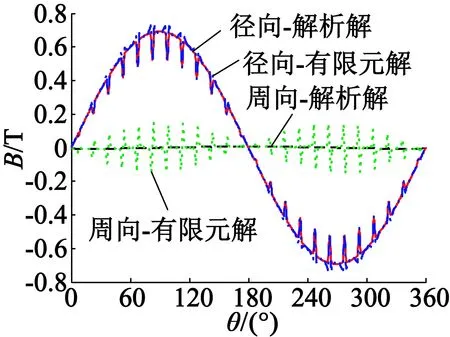
(b) 气隙区域(r= 46.5 mm)

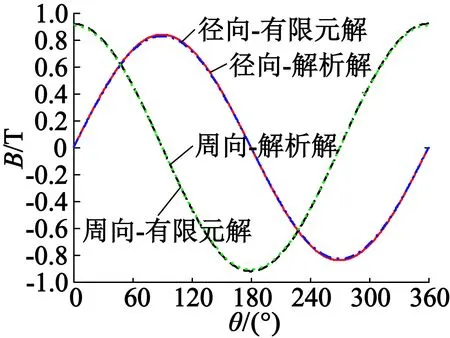
(c) 永磁体区域(r= 22 mm)

对仿真得到的各向气隙磁密进行快速傅里叶变换，将基波分量与解析模型计算出的气隙磁密进行对比，如图5所示。可以看出，不管是距离定子内径较远处，还是靠近定子内径处，气隙磁密的解析解和其基波的有限元解都是一致的，进一步验证了解析模型的正确性。这样，在电机初始设计前期，可以利用式(15)方便且精确地计算出定子内径处的径向气隙磁密，结合相关参数进一步得到电机的空载反电动势，从而在有限元仿真分析之前简捷快速地验证方案的合理性，了解参数调整的大致范围和方向，有效地节约时间和提高设计精度。

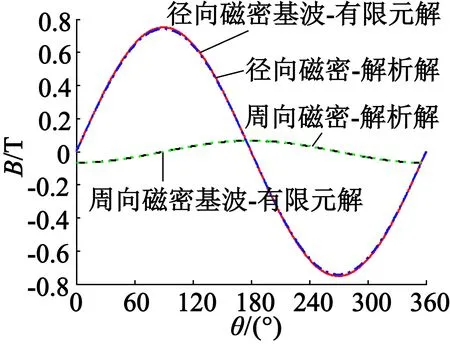
(a) r= 43 mm

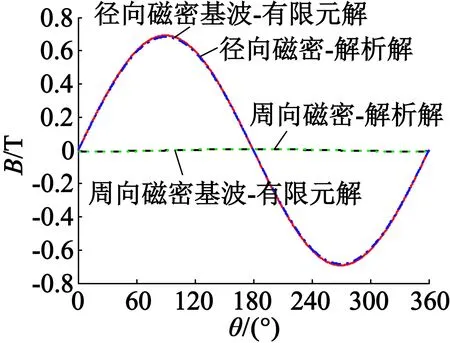
(b) r= 46.5 mm

在电磁场分析软件Ansoft Maxwell中只建立永磁体的有限元模型，进行转子置于空气中时静磁场的仿真计算，得到永磁体外部区域以及永磁体区域各向磁通密度分布，与本文解析模型计算结果的对比如图6所示，可以看出，解析解和有限元解同样吻合地非常好。当转子置于空气中时，磁通密度仍然是标准的正弦波形，在永磁体外部，磁密径向分量和周向分量的幅值相等，相位相差-π/2。样机转子永磁体充磁后，在空气中利用高斯计测量转子保护套表面的磁感应强度，根据式(19)快速求取磁密计算值并与测量值进行比较，从而方便地检测转子永磁体的充磁效果。

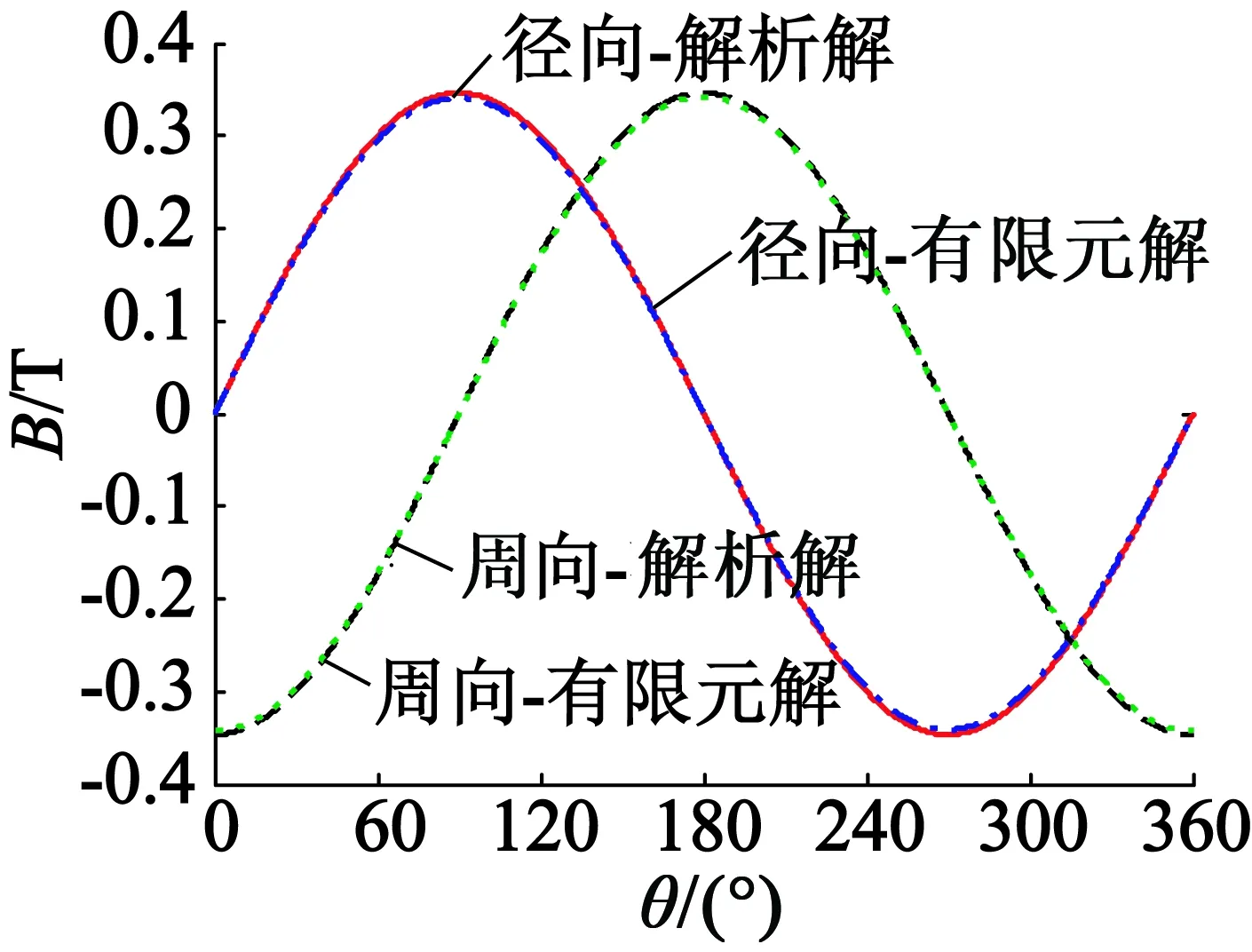
(a) 永磁体外部(r= 46.5 mm)

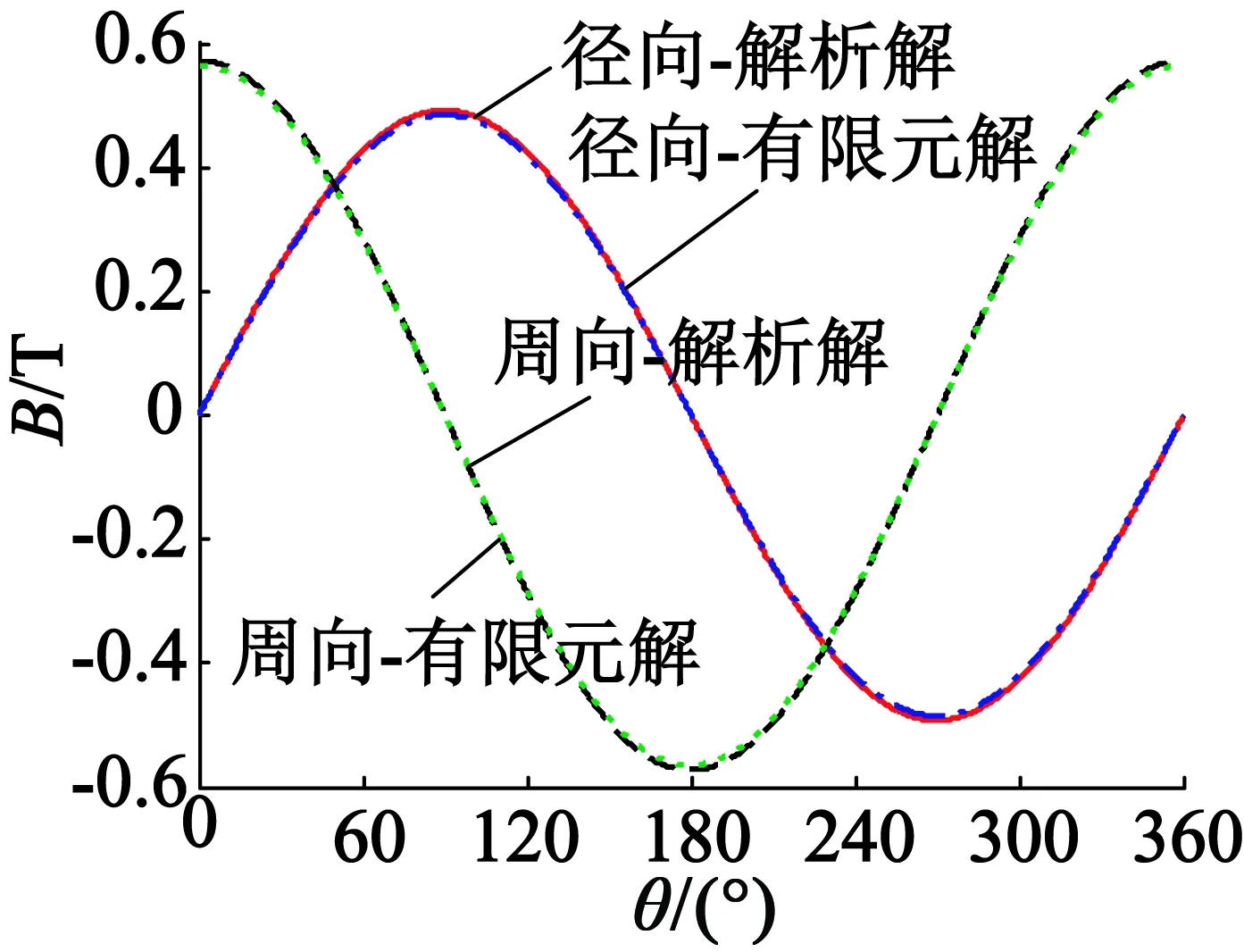
(b) 永磁体区域(r= 22 mm)

由以上分析可知，和两极平行充磁SCPM[12]以及内装导磁心轴的两极平行充磁RSPM[12]一样，内装不导磁心轴的两极平行充磁RSPM，不管是置于定子腔还是空气中，产生的磁场也是标准的正弦波形，大大减少了气隙中的谐波磁场，从而对改善电机的振动与噪声、电磁转矩波动，降低电机的电磁损耗等都有较大的作用，而这些对于高速和超高速永磁电机来说是很重要的。

3 转子尺寸对径向磁密的影响

对于表1的样机，当转子置于定子腔中时，利用本文解析模型计算出的定子内径和气隙中心(r= (Rp+Rs)/2)处径向磁密幅值随转子尺寸的变化关系如图7所示。当转子置于空气中时，利用解析模型计算出的r= 42.5 mm处径向磁密幅值随转子尺寸的变化关系如图8所示。从图7和图8中可以看出，两种情形下，径向磁密均随着永磁体外半径的增加和心轴外半径(等于永磁体内半径)的减小而增大，但是相比后者，永磁体外半径的影响更大。情形1中，永磁体外半径从37.5 mm增加到38.5 mm(心轴外半径Rf=6 mm)，定子内径处和气隙中心处的径向磁密幅值均增加了5.600 6%，心轴外半径从6.5 mm减小到5.5 mm(永磁体外半径Rp=38 mm)，两处的径向磁密幅值均仅增加0.864 1%。对于情形2，永磁体外半径从37.5 mm增加到38.5 mm(心轴外半径Rf=6 mm)，所考察半径处径向磁密的幅值增加了5.546 4%，而心轴外半径从6.5 mm减小到5.5 mm(永磁体外半径Rp=38 mm)，同样位置处径向磁密的幅值仅增加0.855 9%。这是因为沿半径方向将永磁体外半径和内半径分别增加同样的厚度，永磁体体积的增加量却是不同的。由此可知，在同类电机的初步设计中，为满足电机性能指标而需要调整参数时，改动永磁体的外半径将获得更为明显的效果。

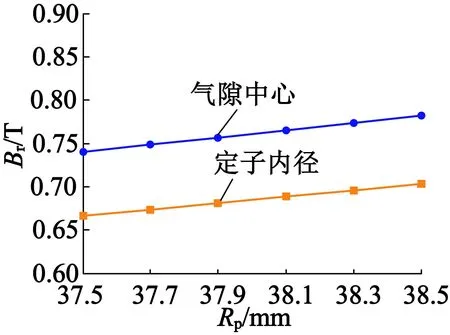
(a) 径向磁密幅值随永磁体外半径变化的关系

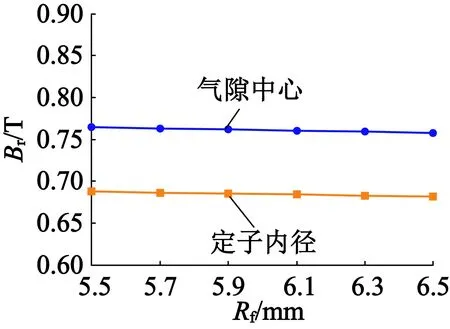
(b) 径向磁密幅值随心轴外半径变化的关系

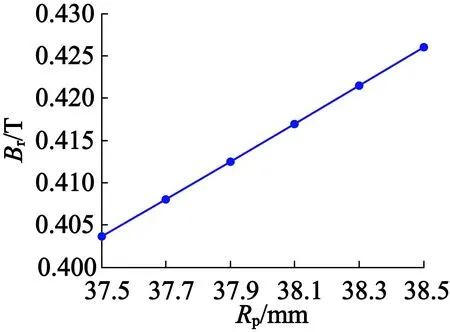
(a) 径向磁密幅值随永磁体

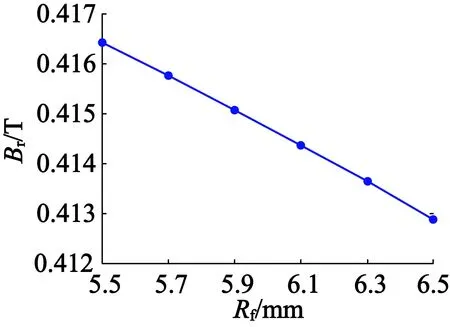
(b) 径向磁密幅值随心轴

4 结 语

对于内装不导磁心轴的两极平行充磁RSPM，不管是置于定子腔还是空气中，产生的磁场均为标准的正弦波形，这在很大程度上改善了电机的电磁性能。磁通密度的解析计算结果与有限元计算结果一致，验证了解析模型的正确性。

对于内装不导磁心轴的两极平行充磁RSPM，置于定子腔中时的径向气隙磁密和置于空气中时外部空气中的径向磁密均随着永磁体外半径的增加和心轴外半径的减小而增大，但是相比后者，永磁体外半径的影响更大，因此在同类电机的初步设计中，为满足电机性能指标而需要调整参数时，改动永磁体的外半径将获得更为明显的效果。利用本文解析模型可以快速且精确地计算气隙磁密(永磁体置于定子腔中)以及永磁体外部磁密(永磁体置于空气中)，为电机的设计和优化提供依据，并且便于检测样机转子永磁体的充磁效果。另外，本文解析模型也为继续研究该结构类型的高速/超高速永磁同步电机的相关特性提供了条件和便利。