海上风电场与航路安全距离

聂园园， 刘克中,b,c， 杨 星,b， 陈蜀喆,b， 马 杰,b

(武汉理工大学 a.航运学院；b.内河航运技术湖北省重点实验室； c.国家水运安全工程技术研究中心， 武汉 430063)

随着海上风电的快速发展，海上风电场建设占用可航水域的面积也在逐渐增加，海上风电场水域船舶通航安全也越来越受到人们的关注。在进行海上风电场选址时，合理地设置拟建海上风电场与航路的安全距离是保障风电场附近船舶通航安全的最直接有效的措施，已成为海上船舶安全航行研究领域备受关注的问题之一。[1-4]

相对于海上石油平台和桥梁而言，海上风电场建设起步较晚，因此，在海上设施与航路安全距离定量研究方面，针对石油平台或桥梁的研究占大多数，而对于海上风电场的研究相对较少。例如，朱曼等[5]在分析失控船舶漂移运动模型的基础上，建立失控船舶-桥碰撞概率计算模型，并根据可接受碰撞概率定量获取桥区水域的通航范围。HASSEL等[6]为研究船舶与石油平台的安全距离，对平台建设前后附近水域的船舶交通流数据进行统计分析，研究结果表明:在平台建成后，大多数船舶自觉地与平台保持1 n mile以上的通行距离。学者们在确定海上风电场与航路安全距离时往往会参照相关国际公约、法律法规以及行业规定等，或借鉴其他海上设施的研究成果，直接设定为某一具体范围。[7-8]目前，也存在一些学者在研究海上风电场水域船舶交通或碰撞风险时，对两者与风电场和航路距离之间的关系进行分析。例如，RAWSON等[2]通过统计Thanet海上风电场建设前后附近的船舶交通分布后，发现在建设前存在部分船舶穿过风电场场区的现象，而在建成后船舶与风电场的距离基本>0.5 n mile。WAWRUCH等[9]在对MARIN和GL碰撞风险模型进行对比分析之后，利用这两种模型计算出风电场和航路距离分别为0 n mile、0.5 n mile和1.0 n mile时的船舶和风机碰撞概率，实现风电场与航路安全距离的基础建模。CHANG等[10]为评价船舶定线对海上风电场水域通航安全的影响，在距离风电场不同位置处选取多个截面，并对各截面上的船舶交通流进行拟合，在此基础上利用IWRAP模型计算出有、无船舶定线时船舶与风电场的碰撞概率。该研究涉及碰撞概率与风电场和航路距离之间的对应关系分析，能够为风电场与航路的安全距离研究提供一种参考思路。

综上所述，现有海上风电场水域船舶航行安全研究对于风电场与航路安全距离的定量分析探索较少，一些学者虽然能从船舶交通分布和船舶碰撞风险的角度进行分析，但研究不够深入，缺少考虑船舶交通流、风、流和风电场规模等因素对安全距离界定的影响。基于此，本文构建全面的船舶与海上风电场碰撞概率计算模型，并根据可接受碰撞概率的标准来界定海上风电场与航路安全距离，从而建立一种满足船舶与风电场碰撞概率处于可接受水平以内的安全距离计算方法，为风电场选址和风电场水域船舶航行风险研究提供理论支持。

1 船舶与风电场碰撞概率计算模型

1.1 船舶与风电场碰撞过程分析

根据船舶主机是否出现故障，可将船舶与风电场碰撞分为漂移碰撞和动力碰撞两种类型。漂移碰撞是指船舶在风电场附近航行时，出现主机故障导致船舶失控，受风、流等环境因子的影响，可能漂移至风电场内与风机发生碰撞。船舶k失控后受到风、流的拖曳力，其漂移速度指向风电场，经过一段时间的漂移将进入风电场内,见图1。船舶k若能在进入风电场前，及时自救或得到外界援助，也可避免发生碰撞。动力碰撞是指由于人为错误、恶劣天气和风机干扰等因素引起的航行失误，船舶在不断接近风电场的过程中未能及时调整航向，船舶机动避碰失败，导致与风电场发生碰撞。在既定航路上航行时，船舶航向改变通常较小，因此，动力碰撞发生的一个前提条件是船舶航行在将与风电场发生碰撞的区域内。船舶j与风电场发生动力碰撞的碰撞区域见图1。

图1 船舶与风电场碰撞过程

1.2 计算模型构建

1.2.1基本模型

基于对碰撞过程的分析，可将船舶与风电场碰撞概率计算模型分为漂移碰撞和动力碰撞概率子模型。通过拆分碰撞过程的不同阶段，在漂移碰撞概率子模型中，需判断船舶是否发生故障、漂移航迹是否朝向风电场及在进入风电场前能否获得救援。在动力碰撞概率子模型中，判断船舶是否位于碰撞区域内，主要取决于船舶位置和船舶航向。驶入碰撞区域上的船舶并不必然会与风电场发生碰撞，因此，还需考虑船员能否及时采取避碰措施。在上述分析的基础上，考虑船舶交通量和船舶类型的影响，构建船舶与风电场碰撞概率计算模型为

P=P1+P2

(1)

(2)

(3)

式(1)～式(3)中：P为船舶与风电场发生碰撞的年平均概率；P1为船舶失控后与风电场发生漂移碰撞的年平均概率；P2为船舶与风电场发生动力碰撞的年平均概率；Ni为航路上第i类船舶的年交通量；Pib为第i类船舶发生失控的概率；x为船舶位置的横坐标(以航路中轴线为纵坐标轴，以垂直于航路中轴线的直线为横坐标轴)；Bi为第i类船舶的平均宽度；f(x)为船舶横向分布的概率密度函数；Pcw为船舶受风、流作用漂移至风电场的概率；PM1为船舶未能成功自救的概率；PM2为船舶未能成功得到外界援助的概率；θ为船舶航向；f(θ)为船舶的航向分布密度函数；θ1、θ2为船舶位于碰撞区域内时航向指向风电场边界时的航向临界值，θ1<θ2；xW1、xW2分别为W1、W2的横坐标；PC为因果概率；Pr为船员无法及时做出避碰反应的概率。

1.2.2主要参数求取

Pib与船舶平均失控概率和船舶在航路上航行的时间有关，即

(4)

式(4)中：Pb为船舶每小时发生失控的概率，可通过统计事故数据获得；L为航路长度；vi为第i类船舶的平均航速。

f(x)可通过统计船舶数据之后对船舶在航路宽度方向的数量进行拟合获得。海上风电场一般建设于开阔水域，对于开阔水域而言，f(x)通常服从正态分布,[9-10]且

(5)

失控船舶在风、流等因素的共同作用下将产生一定的漂移速度，通过判断该漂移速度的方向与风电场方位的一致性能够确定Pcw的大小。其计算公式为

(6)

A={w|vw<0.2 m/s,w∈[1,Nw]}

(7)

式(6)～(7)中：Nw为风向种类数；Nc为流向种类数；Pw为w风向的概率；Pc为c流向的概率；Pa1、Pa2为在w风向和c流向时，失控船漂移速度vd的方向指向风电场的概率，主要与船舶失控位置以及风电场边界长度Lf有关；w∈A指风向种类为静风的情况。

确定vd的大小和方向首先需要掌握失控船舶的受力情况，失控船舶主要受风、流、波的作用，通过对失控船舶进行受力分析，可得到受力公式为

(8)

(9)

(10)

式(8)～式(10)中：M为船舶载重吨；mf为科氏力；Fw为风的拖曳力；FC为水的拖曳力；Fw为波浪辐射力；ρw和ρc分别为空气和海水的密度；Sw和Sc分别为失控船舶暴露于水面以上和浸没于水面以下的面积；Cw和Cc分别为空气和水流的曳力系数。

假设失控船舶在任意时刻都处于平衡状态，即dvd/dt=0，同时，忽略波浪的辐射力和mf，可得到

Fw+Fc=0

(11)

从而推导出vd的大小和vd与vw的夹角α分别见式(12)和式(13)。在Cw/Cc一定时，vd除与vw和vc有关，还与Sw/Sc有关。在船舶满载时，Sw/Sc主要与船舶载重量M有关。

(12)

(13)

船员能通过修理故障，抛锚停航以及获取外界援助等措施，避免与风电场发生碰撞。相关研究[11]通过统计分析，可得出船员未能及时修理船舶主机故障的概率取决于主机故障时间，见式(14)。船员未能通过抛锚阻止船舶漂移的概率随风速的变化关系，也可通过查阅文献得出。[11]

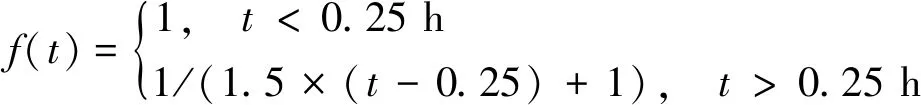
(14)

式(14)中：f(t)为船员没能成功修理故障的概率，主要与vd和船舶与风电场的距离ds有关，vd越大，ds越小，f(t)越大；t为主机故障时间。

外界援助通常指应急拖船的救援行动。PM2主要与拖船吨位Mt、拖船速度vt、拖船与失控船舶的初始距离dt、失控船漂移速度vd和失控船舶载重量M等因素有关，具体为

PM2=f(Mt,vt,dt,vd,M)

(15)

对于P2而言，首先应获得船舶交通横向分布以及船舶航向分布，根据风电场位置和规模，确定船舶在碰撞区域内且航向也指向风电场的概率，通过分析船舶位置、航向与风电场间的几何关系，得出θ1和θ2为

(16)

(17)

式(16)～式(17)中：y为船舶位置的纵坐标；yW1和yW2分别为W1和W2的纵坐标。

PC为船舶采取避碰措施失败的概率，与船舶吨位、速度、导助航设备、通航环境和人为因素等有关，难以进行定量分析。国外相关学者已进行一些研究，FUJII等[12]通过分析历史数据，提取事故发生之前船舶偏移被纠正的频率，从而确定PC的数值。Pr主要取决于ds，借鉴MARIN碰撞模型[13]中的经验公式，认为Pr=exp(-0.575×ds)。

1.2.3蒙特卡洛模拟

蒙特卡洛模拟方法是一种运用随机数解决计算问题的方法，能够通过多次抽样试验获得问题的近似解，在水上交通安全领域中应用广泛。[14-15]通过不断生成服从船舶特征分布、环境特征分布的随机数来计算船舶与风电场碰撞概率。

船舶位置、船舶航向一般服从一个特定分布，可通过实地调研获取。环境因素如风况、流况也遵从一定规律，可从气象网站上获得。在获得船舶特征、环境特征的分布函数之后，分别产生船舶位置、航向、主机状态等特征以及风况、流况的随机数。据此，结合其他相关参数可求得船舶与风电场的碰撞概率。

2 船舶与风电场碰撞概率影响因子分析

通过计算在不同条件下船舶与风电场碰撞概率，分析碰撞概率随各因子的变化趋势，探究船舶与风电场碰撞概率的一般规律，是基于可接受碰撞概率界定航路与风电场安全距离的基础。

整机测试仪通过装置电源把座上的闭环测试连接线，实时检测装置闭锁接点复位信号。当装置上电后，装置闭锁信号会从闭合到断开，表明装置已处于正常运行状态，可以进行整机测试。WDT将装置正常运行信号反馈给ITCC，有其根据信号来源，触发左侧或右侧测试系统的扫描仪。扫描仪扫描装置侧面的机箱条码，并将条码信息提交给大数据服务支撑模块。大数据服务支撑模块根据装置条码获取装置硬件板卡等多维度数据，智能测试控制中心根据该数据控制对应气阀，完成该型号装置测试连接线的自动连接，为整机智能测试构建闭环测试环境。

2.1 试验参数确定

本文以莆田辖区拟建的海上风电场E区为试验对象，通过多组模拟试验验证所提出的计算方法。试验中一些因子的取值见表1，风玫瑰图见图2。

表1 参数取值

图2 风玫瑰图

根据概率模型分析可知:P与诸多因素有关。为从船舶和风电场特征两方面分析P，在梳理P的主要影响因素之后，选取v(船舶平均速度)、M和Lf作为主要参数，深入探索P随主要影响参数的变化规律。根据对风电场E区水域的船舶交通流统计可知:船舶速度通常在6～13 kn，船舶以中小型船舶为主，船舶载重量一般低于2万t。此外，风电场E区靠近航路一侧的边界线长度约为7 000 m。基于以上实际数据，对试验参数进行假设，设计3组试验方案见表2。

表2 试验设计

2.2 试验结果分析

2.2.1P随v的变化

P随v的变化趋势见图3。当M和Lf一定时，若设定某一风电场与航路距离，P随v的增大而减小；当风电场与航路距离d<4 200 m时，v取不同取值时对应的P值之间的差异较为明显，随着d的增加，这种差异也随之缩小。

图3 P随v的变化

2.2.2P随M的变化

P随M的变化趋势见图4。当v和Lf一定时，若设定某一风电场与航路距离，P基本随M的增大而减小。当d<1 000 m或900 m2 400 m时，P几乎不变化，逐渐趋向于0.001。

图4 P随M的变化

2.2.3P随Lf的变化

P随Lf的变化趋势见图5。当v和M一定时，若设定某一风电场与航路距离，P随Lf的增大而增大。当900 m4 800 m时，Lf取不同值时对应的P值之间的差异很小，但仍有所区分。

2.3 试验结论

在以上参数的设置下，得出P的最大值约为0.049艘次/a。在其他参数不变时，P随船舶平均速度的增大而增大，且幅度明显，而随船舶载重吨和风电场边界线长度的变化不明显。

图5P随Lf的变化

3 海上风电场与航路安全距离界定

根据试验结果可知:船舶和风电场碰撞概率与航路和风电场距离密切相关。为保障风电场水域船舶航行安全，可通过控制航路与风电场距离，达到降低船舶与风电场碰撞概率的目的。

本文借鉴德国在海上设施碰撞风险研究中的可接受风险标准[16]，将航路中船舶与海上风电场发生碰撞事故的可接受概率设定为0.006 7艘次/a。据此，计算出满足年平均碰撞概率小于0.006 7艘次时的风电场与航路距离，将其作为安全距离。

在参数设置下，当v、M、Lf取不同值时，风电场与航路安全距离变化趋势见图6。当M、Lf一定时，安全距离随v的增大而减小；当v<8 kn时，安全距离会发生明显波动；当v>8 kn时，安全距离的变化较为平顺。当M、v一定时，安全距离基本上随Lf的增加而增大；当v、Lf一定时，随着M的增大，安全距离逐渐减小。安全距离随v、M、Lf的变化趋势与P的变化规律相对应，在3个参数中，安全距离随v的变化最大，而随Lf的变化最小，说明虽然缩小风电场边界线长度能够降低船舶与风电场碰撞的概率，从而降低对于风电场与航路的安全距离的要求，但成效不大，建议适当提高附近船舶平均速度。

a) M=1 000 t

b) M=5 000 t

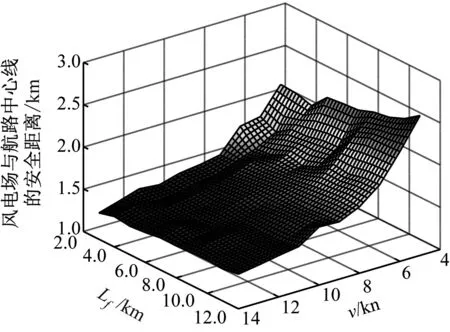
c) M=10 000 t

图6 风电场与航路安全距离变化曲面图

在参数设置下，风电场与航路的安全距离在1 300～3 000 m。相对于英国海事与海岸警卫署提出的安全距离范围[1]，本文得出的安全距离阈值更小，在确保船舶通航安全水平满足行业标准的情况下，所提出的安全距离模型能够更好地优化海域资源配置，同时，能够减小对原船舶交通流的压缩及通航环境的改变，在一定程度上将减少海上风电场建设对船舶通航安全的影响。

4 结束语

在分析船舶与海上风电场碰撞过程的基础上，考虑船舶类型、位置、速度、风和流等因素的影响，建立基于蒙特卡洛仿真的船舶与风电场碰撞概率模型，分析船舶与风电场碰撞概率的分布特征。随后，剖析碰撞概率与风电场和航路的距离之间的相互关系，确定碰撞概率的可接受程度，据此获取风电场与航路的可接受安全距离范围，从而提出一种定量计算海上风电场与航路安全距离的方法。研究结果表明:船舶平均速度越小，船舶载重吨越小，风电场边界线长度越大，风电场与航路的安全距离阈值也越高，特别是当v<8 kn时，安全距离阈值将大幅度提高。