核心素养视角下用问题引领数学实验活动课——以数学活动“正方形纸片的折叠”为例
江苏省徐州市第三十一中学 胡子扬
一、实验目的
设计以问题——“用正方形纸片折出含有30°角的直角三角形”为背景的折纸实验。经历“操作——观察——思考——交流——推理——操作”的过程,探究正方形纸片在翻折前后对应边、角的数量和位置关系,探究图形性质,感悟“用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界”,借助实验助推数学思维生长。
二、实验准备
10cm×10cm 的正方形纸片3 个。
三、实验内容与步骤
第一步:如图1,将正方形纸片ABCD 折叠,使点A 和点B,点D 和点C 重合,将正方形纸片展开后,得折痕MN,如图2。
问题1:折痕MN 和正方形ABCD 的各边有何特殊的数量、位置关系?
问题2:你能在图1 中用尺规作出折痕MN 吗?
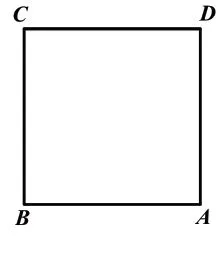
图1

图2
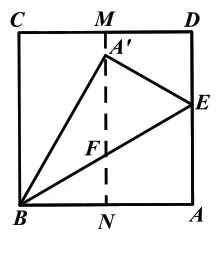
图3
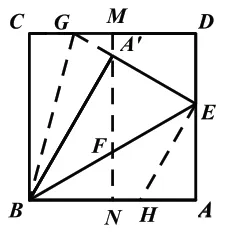
图4
设计意图:从简单的折纸动作入手,由折纸现象联系轴对称的数学性质,得折痕MN 垂直平分边AB、CD ,折痕MN 平行AD、BC;锻炼用尺规作线段垂直平分线的基本数学技能。
第二步:如图3,在边AD 上取一点E,将正方形ABCD 沿BE 折叠,使点A 落在MN 上的点A'处,将正方形纸片展开后,设BE 与折痕MN 相交于点F。
问题3:试用尺规在图2 中作出点A'和点E。
国家要尽快制定一些相关的法律法规,为低碳经济的发展构建一个积极、完善、客观的外部环境,替低碳营销模式提供良好的氛围。现今,世界各国都在相继制定、出台与低碳经济相关的法律、法规。例如美国制定的《低碳经济法案》、英国出台的《可再生能源义务》、丹麦的绿色能源的发展模式和意大利的“白色证书”“绿色证书”、能源计划等等。我国也应该着手这方面立法的研究。在制定相关的法律法规时,添加应对气候变化的相关条款,在规划、批报项目和战略环评的规则中增加气候影响评价的规定,逐渐建立健全应对气候变化的体系。
问题4:在图3 中,连接AA',你认为△ABA'是何三角形?你还能找到图中与之类似的三角形吗?
问题5:图3 中哪些角的度数为30°?
设计意图:培养学生“用数学”的意识:用数学的眼光观察折纸操作,用数学的思维思考现象背后的数学本质。
①联系轴对称的性质,折痕MN 上的点A'有A'B=AB 的特征,故用圆规以点B 为圆心,BA 为半径截取即得。同时关注用尺规作角的角平分线的基本数学技能。
②关注一、二两步操作产生的折痕,即对称轴,由对称轴上的点到线段两端的距离相等,得AB=A'B=AA',从而△ABA'是等边三角形,类似的,可以发现△AEF 也是等边三角形。
③对比折叠前后的线段和角,落实到边角的数量关系上,不难发现∠CBA',∠EBA',∠ABE,∠BA'N,∠AA'N 等均为30°的角。
第三步:将图3 中的正方形再次折叠,使BC 和BA'所在的直线重合;EA 和EB 所在的直线重合,展开后得折痕分别为BG、EH。
问题6:试用尺规在图3 中作出折痕BG、EH。
问题7:问题2 和问题6 中折痕的画法有何异同之处?能把你的经验和方法与同学分享吗?
问题8:观察图4,折叠后点C 和点A'重合吗?为什么?
设计意图:同为折叠产生的折痕作图,但对应点重合产生的折痕与对应边重合产生的折痕落实在作图上是有所区别的,引导学生进一步思考自己的作图操作,并及时总结。同时关注点、线、角的重合前后的对比,落实到线段和角的大小关系和位置关系上,不难证明折叠后点C 和点A'是重合的。
第四步:在第三步折叠的基础上,将纸片再次沿BE、BA'和A'折叠,使其都与△A'BE 重合,则△A'BE 即为所求。
问题9:试说明△A'BE 是含有30°角的直角三角形。
问题10:观察折叠后的纸片,你有什么发现吗?
设计意图:引导学生由前面的操作过程联系数学思考、数学推理,用数学的符号语言规范表达自己的证明过程,将操作的过程、思维可视化;进一步观察、交流、操作,我们可以发现△A'BE 在折叠后的纸片上的内心和斜边上的中线等结论。开放的问题让相异的学生能从不同的角度观察数学现象,联系数学知识,拓展数学思维,提升数学素养。
四、实验指南
本实验是为初中高年级学生设计的一节数学综合活动课.通过折叠正方形纸片,不仅再次从轴对称的角度对正方形的图形性质进行认识,而且在操作过程中逐步经历运算推理,发展空间想象能力及逻辑推理能力。
在折纸操作的过程中回归数学本真,对于生活中的简单纸质现象,能用数学的眼光审视其中蕴含的数学原理;用数学的思维思考在折纸过程中产生的数量和位置关系等数学问题;能用数学的语言描述折纸的现象和数学思想方法。

