近场动力学方法在C/C复合材料烧蚀问题中的应用

陈明伟,刘齐文，2,刘立胜，2

(1.武汉理工大学力学系，湖北 武汉 430070;2.武汉理工大学理学院新材料力学理论与应用湖北省重点实验室，湖北 武汉 430070)

C/C复合材料具有抗烧蚀、抗冲击、高比强度、高比模量等特点，在航天器和武器等飞行器的热防护安全领域得到了广泛的应用，目前正逐步取代传统防热抗烧蚀材料，成为飞行器结构设计中防热结构的主要材料。飞行器在高温、高焓及高热通量等恶劣环境下，如航天器进入大气层时，经受7 000 K左右超高温、几十兆瓦热通量、100个标准重力加速度的过载，此时通过材料自身热化学烧蚀以及机械剥蚀引起质量损失，带走大部分的热量，阻止外部热量向飞行器内部传递，从而保护内部工作人员的安全与内部结构的正常工作[1]。鉴于C/C复合材料在飞行器安全领域中应用的重要性，目前对C/C复合材料的研究也愈加广泛。通过对C/C复合材料热化学烧蚀性能的研究，可增加对其内部结构及其服役性能的了解，以为飞行器热防护材料的设计和研究提供理论支持。

C/C复合材料在高热通量条件下，由于材料本身与高热气流的物理、化学和力学作用等，会发生质量损失。目前，针对C/C复合材料的烧蚀研究，已经提出了一些有效的烧蚀计算模型，并可以计算在一定烧蚀条件下材料的线烧蚀率[2]。现有主要的烧蚀模型有热化学烧蚀模型、机械剥蚀模型等[3-4]。根据热化学烧蚀理论可以对C/C复合材料的热化学烧蚀行为进行建模，并对材料的质量损失与线烧蚀率的变化规律进行理论上的预测[5]。

C/C复合材料的烧蚀过程是一个包括质量损失和结构失效的复杂过程，是一个非常典型的非线性、不连续问题[6-7]。目前对此类问题的研究主要有实验和数值模拟两种方法，但实验方法条件苛刻、经济成本过高，而数值模拟方法则恰好弥补了实验方法的缺点，又可满足一定的精度。数值模拟方法近年来发展迅速，已被广泛应用于生物、建筑、机械等多个领域。如徐迟等[8]和陈超等[9]利用数值模拟方法分别模拟计算了三峡库区某滑坡库水位与降雨联合作用渗流应力耦合和汽车油罐车爆炸燃烧特性，获得了较好的计算精度。此外，在处理不连续问题时，传统的有限单元法、有限差分法等一些宏观方法的计算结果主要依赖于网格尺寸及质量[10]。烧蚀问题包含边界移动，在烧蚀发生后，因材料的质量损失也必须重新划分网格，计算结果也具有强烈的网格依赖性。而近场动力学(peridynamics,PD)理论的提出与发展突破了经典理论的限制，它基于非局域思想建模，采用空间积分方程代替偏微分方程来描述物质点的运动，自然而然地得到对不连续现象的描述，从而可以避免传统计算方法的奇异性和计算效率的问题[11-12]。PD方法经过多年的发展，已成功运用于许多研究领域。如Ha等[13]采用基于键型PD理论研究了动态脆性裂纹问题；Oterkus等[14]采用基于常规态的PD方法研究了热扩散的问题；Bobaru等[15]采用基于键型PD方法研究了瞬态热传导问题;廖洋等[16]采用PD强度折减法分析了边坡的稳定性问题；王超聪等[17]采用PD方法对复合材料的烧蚀温度场进行了模拟。

本文在C/C复合材料热化学烧蚀理论的基础上，建立了C/C复合材料在热化学烧蚀与温度场相互耦合条件下的PD求解模型。首先，根据热化学烧蚀理论计算进入C/C复合材料模型内部的净热流；然后，根据净热流进一步由PD传热理论计算移动边界条件下C/C复合材料的烧蚀温度场。在对烧蚀表面退缩问题求解时，满足烧蚀判据的粒子自动脱落，进而实现了烧蚀面的移动，可以直观地表征烧蚀移动边界条件下瞬态温度场的分布。

1 C/C复合材料的热化学烧蚀计算

1. 1 表面化学反应

C/C复合材料的热化学烧蚀主要包括碳的氧化反应、升华、碳氮反应以及空气中氮气和氧气的分解反应。

热力学分析表明，C/C复合材料在发生热化学烧蚀时的主要化学反应包括：

iC(s)→Ci(g)(i=1,2,3)

(1)

O2→2[O]

(2)

N2→2[N]

(3)

上式中：C(s)为固态碳；Ci为升华碳对应分子：C1、C2、C3，且式(1)中包含三个反应式；O2为氧气分子；[O]为氧离子；N2为氮气分子；[N]为氮离子；s表示组元为固态；g表示组元为气态。

(4)

(5)

(6)

上式中：C2N、CN、CO为相应反应生成物。

与反应方程式(1)～(6)相对应的平衡常数k分别为

kpci=pci(i=1,2,3)

(7)

(8)

(9)

(10)

(11)

(12)

上式中：pC1、pC2、pC3、pCO、pO2、pC2N、pN2、pCN、pO、pN为对应的各组元相对分压。

平衡常数k仅仅与温度相关，可通过查阅《物理化学手册》得到各反应的平衡常数与温度的关系式；公式(7)～(12)有8个方程和10个未知数，因此需要补充质量守恒方程来封闭方程组。引入质量浓度ci(单位为1)，ci与组元分压的关系(可直接由物态方程导出)为

(13)

1. 2 相容性条件

在热化学烧蚀条件下，对于具有i种组元的反应系统，表面元素组元的质量守恒方程的形式为

(14)

由热化学边界层理论，在Le=Pr=1(Le为路易斯数，Pr为普朗特数)的条件下，有以下壁面质量守恒条件，即相容性条件：

(1+B)ciw=cie

(15)

式中：e代表反应边界；ci为对应组元的质量浓度；B为无因次质量损失率，其表达式为

(16)

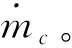
1. 3 表面能量平衡

在进行热化学烧蚀计算时，首先根据上个时刻的热流密度条件利用PD传热理论得到在下一个时刻的壁面温度， 然后计算该温度条件下相应的各个物理化学参数，最后通过C/C复合材料表面能量平衡方程求得进入C/C复合材料壁面内部的净热流，至此可完成一个完整的循环，反应壁面的能量平衡见图1。

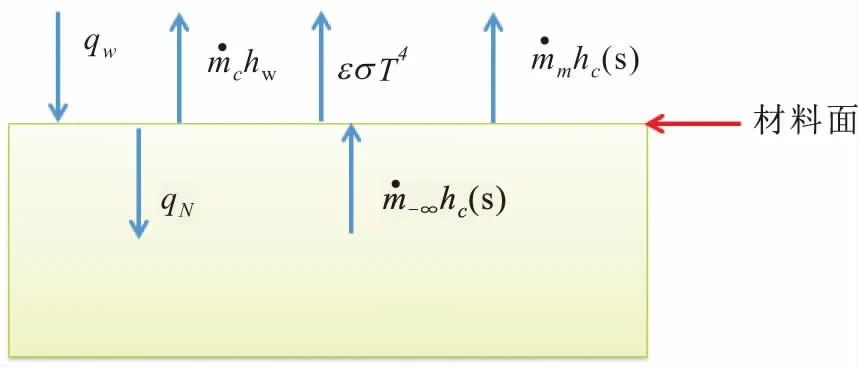
图1 反应壁面的能量平衡示意图Fig.1 Schematic diagram of wall energy balance

由图1可以写出C/C复合材料表面热化学烧蚀的能量守恒关系式，即净热流表达式:

(17)

1. 4 表面烧蚀率

C/C复合材料的烧蚀特性是通过烧蚀率来表示的，当C/C复合材料表面在进行热化学烧蚀时，会伴随着机械剥蚀的发生，根据试验测定的经验关系式为

(18)

(19)

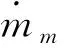
求解出材料总的固体质量损失率后，即可由下式计算材料的表面烧蚀率v-∞(m/s)：

(20)

式中：ρ为材料的密度(kg/m3)。

2 移动边界下模型温度场的计算

2.1 基于第一近邻非常规态的PD温度场的计算

2014年，Oterkus等[14]推导出一种拉格朗日形式的基于常规态的近场动力学瞬态热传导方程：

(21)

式中：ρ为材料的密度(kg/m3);cH为材料的比热容[J/(kg·K)];h为热流态;hs(x,t)为质点x的单位时间热生成量。

若假设当物质点邻域半径较小时，物质点x邻域内各处的温度梯度G近似相等，同时认为只有最近邻的物质点间存在热量的传递[18]，如图2所示，Δ为粒子间距，蓝色区域内粒子仅与红色区域内粒子发生热传递。

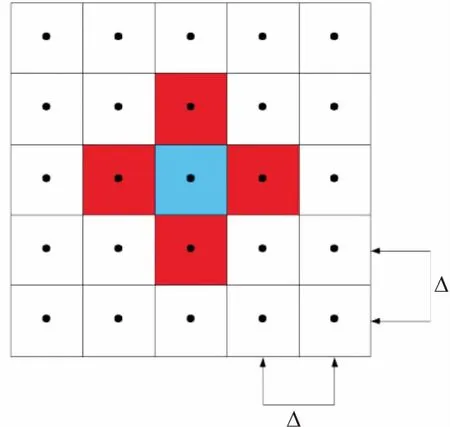
图2 近场动力学瞬态热传导理论的质点邻域Fig.2 Particle neighborhood of peridynamics transient heat conduction theory

依据经典的热传导平衡方程,可以得到第一近邻非常规态的近场动力学瞬态热传导平衡方程如下：

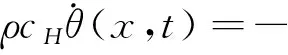
(22)

式中：hs为物质点x的单位时间热生成量。

热流密度的散度表示如下：

(23)

如果边界Rt被施加了热流qb，边界上质点的热流密度为

qi=qb(i∈Ri)

(24)

由此,即可计算模型的瞬态温度场。

2. 2 移动边界的实现

采用PD理论实现烧蚀边界的移动并不需要删除网格、重建网格，这是由于模型是由物质点组成的，在由热化学烧蚀计算得到烧蚀率v-∞后，可由时间积分得到模型的烧蚀深度。由每个时间步烧蚀率叠加得到模型的烧蚀深度，即可得到烧蚀安全区为

(25)

式中:H为材料的原始厚度(m)；Hi为烧蚀后材料的厚度(m)。

若物质点在烧蚀区内(即粒子yi坐标值大于Hi)，则时间相关函数为

(26)

则当μ=0时，粒子脱落，烧蚀发生，实现边界移动；当μ=1时，粒子不脱落，不发生烧蚀。

3 C/C复合材料热化学烧蚀与温度场的耦合分析

C/C复合材料的烧蚀涉及到热化学烧蚀计算和温度场的计算，而传热计算为热化学烧蚀计算提供了反应温度Tw，即

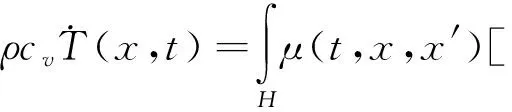
h(x′,t)]dAx′+hs(x,t)

(27)

公式(17)关于C/C复合材料表面热化学烧蚀计算为传热计算提供了热流边界条件qN，对于烧蚀层粒子而言，其热流密度为

qy=qN

(28)

因此,可以对C/C复合材料的烧蚀和温度场进行耦合求解。具体耦合求解流程如下(见图3)：

(1) 设置初始条件，生成邻域，利用PD理论对温度场进行求解，得到当前时刻的壁面温度Tw。

(2) 由壁面温度Tw代入热化学烧蚀计算公式，求得该时间步的表面烧蚀率v-∞和进入材料内部的净热流qN，并判断烧蚀安全区Hi。

(3) 增加一个时间步Δt，判断下一时刻t是否大于总的计算时间t总，然后决定结束计算或者进行下一个时间步的计算。

(4) 搜索粒子形成邻域，将净热流qN作为边界条件施加到更新模型的烧蚀层粒子上,并耦合PD热传导方程,求解当前时间步的壁面温度Tw。

(5) 重复上述步骤(2)～(4)。

图3 C/C复合材料热化学烧蚀与温度场的耦合计算流程图Fig.3 Flow chart for coupling calculation of ablation and temperature field of C/C composites

4 算例计算与分析

4. 1 计算模型与算例条件

参考文献[19]的计算模型，并将其简化为二维计算模型，采用本文中的计算方法对模型温度场、烧蚀率以及进入C/C复合材料内部的净热流等进行计算，并将数值模拟计算结果与文献[19]中的试验结果进行了对比。计算模型采用文献[19]中试验测得的变物性参数，具体如下：

导热率K为

Kx=172.528-0.236T+1.994×10-5T2-7.792×10-9T3+1.14×10-11T4

Ky=82.785-0.103T+9.846×10-6T2-4.372×10-9T3+7.315×10-13T4

式中：Kx、Ky分别为x、y方向的导热率[W/(m2·K)];T为温度(K)。

比热容C[J/(kg·K)]为

C=997+2.930×10-2T

根据能量守恒，给定热流的边界条件为

q=qN

(29)

其中,qN由热化学烧蚀计算以及壁面能量平衡方程计算得到，当y=0时，温度边界为Ty=0=300 K。

其他边界设定为自由边界条件,即

q=0

(30)

表1为算例条件以及数值模拟计算结果与试验结果的对比。本文在驻点压力Ps为0.598 MPa、热焓Hs为8 051 kJ/kg的条件下，对C/C复合材料的热化学烧蚀性能进行分析。计算模型的尺寸为0.050 5 m(长)×0.016 m(宽)，计算y方向与热流方向平行，见图4。

表1 算例条件及数值模拟计算结果与试验结果的对比

图4 计算模型Fig.4 Calculation model

图5为离散后的数值模型，该模型中粒子数为m(506)×n(161)=81 466，粒子间距为0.000 1 m；背景单元大小为0.000 1 m×0.000 1 m，数目为80 800，这里所说的背景单元只是粒子分布的方式，实际上并不存在也不参与计算。

图5 离散后的数值模型Fig.5 Discreted numerical model

4. 2 温度场分布结果与分析

图6为不同时刻(7 s、14 s、21 s和28 s)模型烧蚀温度场分布。

由图6可见，PD方法可以实现对烧蚀边界移动的自然描述。

图6 不同时刻模型烧蚀温度场分布Fig.6 Temperature field distribution of the ablation model at different times

与图6相对应的温度场分布曲线见图7，即为不同时刻模型x=0.008时沿y方向的温度分布。

由图7可见，随着烧蚀时间的增加，温度逐渐趋于线性分布，C/C复合材料的烧蚀率随着反应的进行也趋于一个常数。

图7 不同时刻模型x=0.008时沿y方向的温度分布Fig.7 Temperature distribution of the model along y-direction at different times

4. 3 热化学烧蚀计算结果与分析

图8为不同时刻进入C/C复合材料模型内部的净热流计算结果。

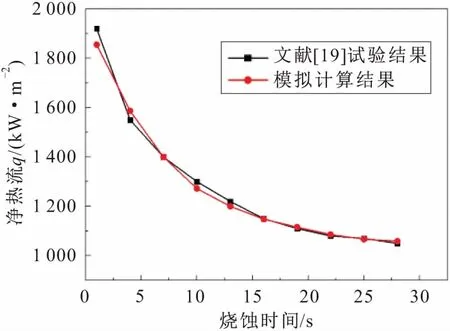
图8 不同时刻进入C/C复合材料模型内部的净热流Fig.8 Net heat flow into the C/C composites model at different times

由图8可见，随着烧蚀时间的增加，C/C复合材料的表面温度不断增加，材料与空气的反应更加充分，带走更多的热量，导致进入C/C复合材料内部的净热流逐渐降低，其与文献[19]中的试验结果进行对比，两者结果相符。

图9为不同时刻C/C复合材料的壁面温度计算结果。

图9 不同时刻C/C复合材料的壁面温度Fig.9 Wall temperature of the C/C composites at different times

由图9可见，烧蚀开始时，C/C复合材料表面温度迅速上升，随着化学反应的进行，带走部分热量，导致温度上升速率逐渐变小；后期随着烧蚀时间的增加，化学反应、壁面温度以及进入C/C复合材料内部的净热流达到动态平衡，材料表面温度会逐渐趋于稳定在2 431 K左右，与表1中试验结果进行对比，两者结果是相符的。

图10为不同时刻C/C复合材料的线烧蚀率(v-∞)计算结果。

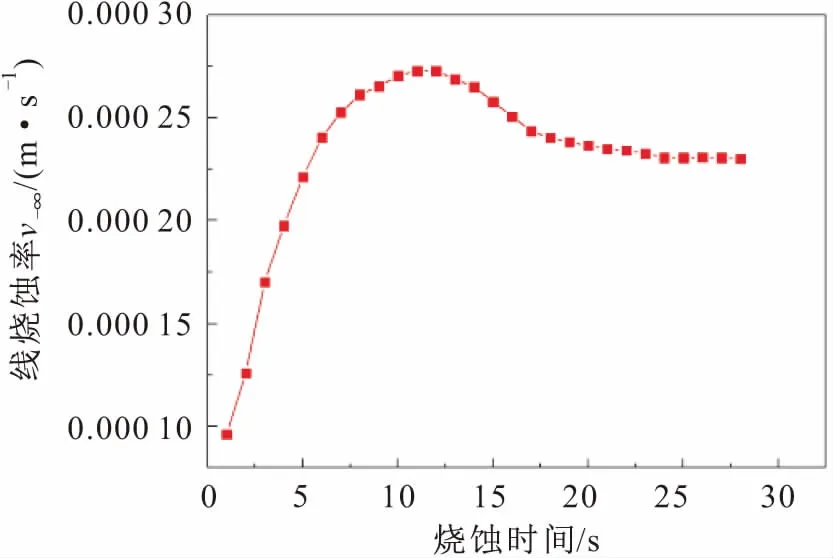
图10 不同时刻C/C复合材料的线烧蚀率Fig.10 Line ablation rate of the C/C composites at different times

由图10可见，热化学烧蚀刚开始时，C/C复合材料的线壁面温度较低，反应缓慢，烧蚀率低；随着烧蚀时间的增加，壁面温度上升，化学反应速度增大，反应迅速，C/C复合材料的线烧蚀率升高；最后整个过程达到动态平衡，C/C复合材料的线烧蚀率趋于稳定，且与表1中试验结果相符。

5 结 论

通过以上算例计算结果与试验结果的对比，可得到如下结论：

(1) 本文提出的基于热化学烧蚀理论的PD传热方法，在引入损伤函数后，实现了对烧蚀边界的自然描述，不需要引入其他复杂判定条件。利用该方法对C/C复合材料的壁面温度、净热流、烧蚀率进行求解，其计算结果与试验结果基本吻合，说明PD方法可用于C/C复合材料热化学烧蚀与温度场的耦合分析。

(2) C/C复合材料的烧蚀与壁面温度、各组元热焓、分压、加载热流及材料性质有关，是多种因素共同作用、相互影响的结果。随着烧蚀时间的增加，各种作用达到一个动态平衡的状态，壁面温度与壁面各组元热化学反应速率趋于稳定， 从而导致C/C复合材料的烧蚀率趋于一个恒定值。